Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

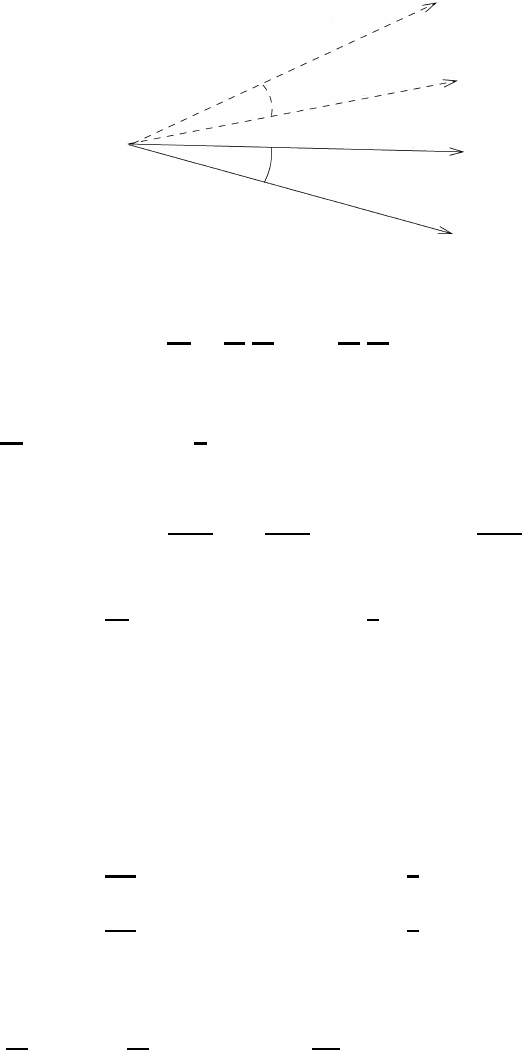
4.3 Individual changes with time of geometric ﬂuid conﬁgurations 201

γ + δγ

)

+ δt)

Fig. 4.6 The change in direction between two material ﬂuid elements.

so that

δr

(

δr) −

δr

(

δr)(4.39)

By use of equations (4.34) and (4.37) we ﬁnd without difﬁculty

= e · (

+ D

) +

(∇×v) × e − e(e ·

· e + e · D

· e)(4.40)

The manipulations with the isotropic part of the deformation dyadic D

e · D

= e ·

∇·v

ee =

∇·v

e, e ·

· e =

∇·v

(4.41)

lead to the desired result

= e ·

− e(e · D

· e) +

(∇×v) × e (4.42)

giving the change with time of the direction of the material ﬂuid element. Recall

that de/dt is perpendicular to the unit vector e itself. Equation (4.42) shows that

the change in direction with time depends only on the anisotropic part of the

deformation dyadic and on the rotation vector.

An immediate application of (4.42) lies in the possibility of calculating the

change of the angle γ between two line elements, see Figure 4.6. On applying

(4.42) to the two directions we ﬁnd at once

(a)

= e

· D

− e

· D

· e

) +

(∇×v) × e

(b)

= e

· D

− e

· D

· e

) +

(∇×v) × e

(4.43)

Scalar multiplication of parts (a) and (b) by e

and e

, and then adding the results,

gives

· e

) =

(cos γ ) =−sin γ

dγ

= 2e

· D

· e

− (e

· D

· e

+ e

· D

· e

)cosγ

(4.44)

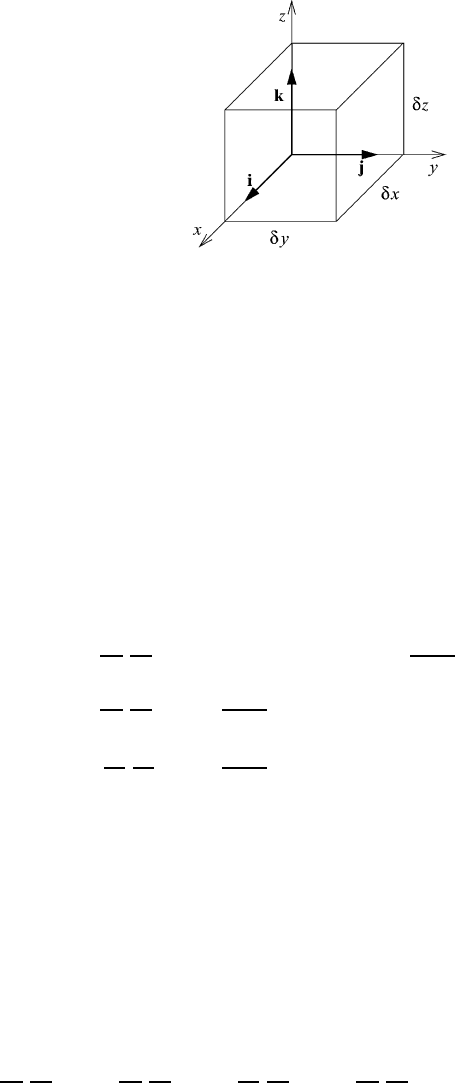
202 Atmospheric ﬂow ﬁelds

Fig. 4.7 A three-dimensional box with sides δx,δy,andδz.

since the rotational parts cancel out. Inspection of this equation shows that the

angular change is caused solely by the anisotropic part of the deformation tensor.

4.3.3 The change in volume of a rectangular ﬂuid box

In this case the application of equation (4.37) is particularly simple due to the

rectangular system. We consider the relative changes of the three sides of the

rectangular box shown in Figure 4.7.

On splitting the deformational dyadic into the isotropic and anisotropic parts we

ﬁnd from (4.36)

δx

(

δx) = i · D

· i + i · D

· i =

∇·v

+ (D

)

δy

(

δy) =

∇·v

+ (D

)

δz

(

δz) =

∇·v

+ (D

)

(4.45)

where we have used the explicit representations of

and D

listed in (4.5). The

are the measure numbers of the dyadic D

. On forming the trace of the matrix

, which is the same as summing the diagonal elements, we ﬁnd immediately

)

+ (D

)

+ (D

)

= (D

)

= 0(4.46)

so that the total deformation amounts to the three-dimensional velocity divergence

δx

(

δx) +

δy

(

δy) +

δz

(

δz) =

δτ

(

δτ ) =∇·v = (D

)

(4.47)

4.3 Individual changes with time of geometric ﬂuid conﬁgurations 203

For the special case that the divergence vanishes we ﬁnd from (4.45) that the relative

change in volume is zero:

δτ

(

δτ ) = (D

)

+ (D

)

+ (D

)

= 0(4.48)

Therefore, a volume-true deformation (the relative change vanishes) of the three-

dimensional box is described by three measure numbers, which are located on the

diagonal of the dyadic

. We consider the brief example

)

= 0 =⇒ (D

)

=−(D

)

δx

(δx) = 0

if (D

)

< 0 =⇒ (D

)

> 0

(4.49)

This means that a decrease in length in the y-direction is accompanied by an

increase in length in the z-direction. These changes take place in such a way that the

total volume remains constant, which is called a volume-true change.Moreover,

the volume remains rectangular.

Let us now brieﬂy discuss the situation in which the form of the box changes.

Since the box originally was rectangular, equation (4.44) simpliﬁes because the

cosine term vanishes. For the angular changes we ﬁnd from (4.44) using (4.5) the

simple relations

(γ

) =−2i · D

· j =−2(D

)

(γ

) =−2i · D

· k =−2(D

)

(γ

) =−2j · D

· k =−2(D

)

(4.50)

We recognize that the off-diagonal elements of the coefﬁcient matrix of D

are

responsible for the volume-true changes of the three angles.

Many additional examples could be given, such as the relative change in volume

of a ﬂuid sphere. As should be expected, the change in volume is again equal to

the divergence.

A brief summary of our results may be helpful. With reference to (4.12) we

observe

v(P



) = v(P ) + δr · D

+ δr · D

(∇×v) × δr (4.51)

so that the general motion of a ﬂuid element consists of

(1) Rigid translation: v(P ).

(2) Dilatation: v

DIL

= δr · D

= δr ·

∇·vE, form-invariant change in volume.

(3) Distortion: v

DIS

= δr · D

(a) Owing to the (D

)

elements a deformation whereby angles and volume do not

change occurs.

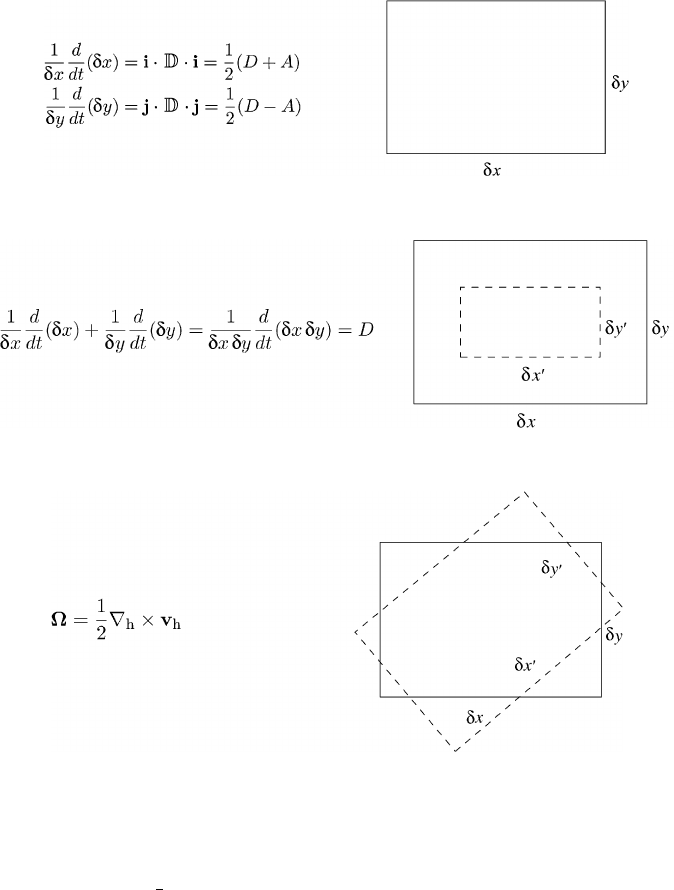
204 Atmospheric ﬂow ﬁelds

Fig. 4.8(a) Length changes of the sides of a rectangle.

Fig. 4.8(b) A change in area of a rectangle.

Fig. 4.8(c) Rigid rotation of a rectangle, D = 0.

(b) Owing to the (D

)

(i = j) elements a distortion occurs but the volume remains

unchanged.

(4) Rotation: v

ROT

(∇×v) × δr, rigid rotation.

4.3.4 Two-dimensional examples

In order to demonstrate more completely the geometric meaning of the principal

deformation quantities A and B, see equation (4.9), we consider several special

areal expansions. The results are collected in Figures 4.8(a)–(e). Part (a) follows

directly from (4.37) on identifying the unit vector e with the Cartesian unit vectors.

Veriﬁcation is easily accomplished by expanding the two-dimensional deformation

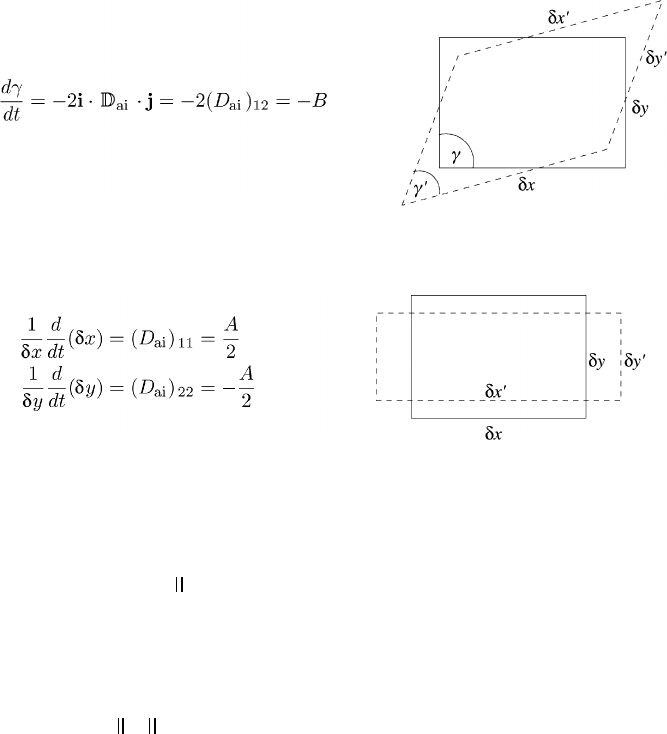
4.4 Problems 205

Fig. 4.8(d) A change in angle between two sides of a rectangle without a change in area,

D = 0.

Fig. 4.8(e) A change in form of a rectangle, with no change in angle and area, D = 0.

dyadic according to (4.8). Part (b) is veriﬁed with the help of (4.47) by omitting the

height term. Part (c) shows a rigid rotation with the angular velocity Ω due to the

antisymmetric dyadic 

, see (4.12). Part (d) follows from (4.44) since the cosine

term vanishes. Part (e) results from (4.48) on specializing to two dimensions.

4.4 Problems

4.1: Show that 

·· = (∇×v)

4.2: Verify equations (4.9d) and (4.9e).

4.3: Consider the initial (x, y)-coordinate system. Rotate this system by a ﬁxed

angle θ to obtain the rotated (x



)-coordinate system. Differentiation of (x,y)

and (x



) with respect to time gives a relation between the velocity components

(u, v)and(u



). Show that the divergence and the vorticity are invariant under

the rotation, i.e. D = D



,ζ= ζ



4.4: Derive (4.33b) and (4.33c).

4.5: Assume (a) a line element in the (x,y)-plane, (b) a surface element in the

(x,y)-plane, and (c) a volume element in (x,y, z)-space. Verify equation (4.33).

The Navier–Stokes stress tensor

In this chapter we are going to derive the connection between the Navier–Stokes

stress tensor J and the deformation dyadic (tensor) D. Once more, the paramount

importance of the local velocity dyadic becomes apparent. First of all, it will be

necessary to introduce the general stress tensor T which includes J.

5.1 The general stress tensor

The description of deformable media requires the deﬁnition of internal and

external forces. Internal forces are molecular-type forces between mass elements,

which may be excluded from our considerations. Owing to Newton’s principle

actio = reactio the net effect of these forces adds up to zero when we integrate

over a speciﬁed volume of the continuum. There exist two types of external

forces.

5.1.1 Volume forces

These forces are proportional to the mass. As is customary, we deﬁne these with

respect to the unit mass and denote them by the symbol f

. In general, we distinguish

between attractive and inertial forces.

(a) Attractive forces due to the presence of the earth and other celestial bodies. The

gravitational pulls due to the sun and the moon are accounted for only if tidal effects

are considered. These are real forces since they are caused by the interaction of an

atmospheric particle with other bodies.

(b) Inertial forces such as the Coriolis force and the centrifugal force. These are ﬁctitious

forces and stem from the rotating coordinate system used to describe the motion of the

particle.

206

5.1 The general stress tensor 207

5.1.2 Surface forces

These forces act in directions normal and tangential to a surface. They will be

deﬁned with respect to unit area and denoted by p

. In the atmosphere we have to

deal with two types of surface forces.

(a) The pressure force p

(p) results from the action of the all-directional atmospheric

pressure. It is always acting in the direction opposite to the normal of a surface element

of the ﬂuid volume to which it is applied. If n is the unit normal deﬁning the direction

of the surface, then we must have

=−pn (5.1)

On identifying n in succession by the Cartesian unit vectors i, j,andk we recognize

the local isotropy of the pressure ﬁeld since in each case we ﬁnd

(p)

= p.

(b) The frictional stress force p

) is a type of surface force that depends on the motion

of the ﬂuid (gas) and on the orientation of the surface to which it is applied. In contrast

to p

(p) the frictional stress is not limited to the perpendicular direction, but acts also

tangentially

to the surface of the

ﬂuid volume. p

) may be represented by the linear

vector function

= n · J (5. 2)

where J is the viscous stress tensor or dyadic which was introduced previously. Sum-

ming up, we ﬁnd for the surf

ace force

+ p

=−pn · E + n · J = n · T

with T =−pE + J =−pi

+ τ

(5.3)

where T is the general stres

s tensor which also includes the effect of pressu

re. The

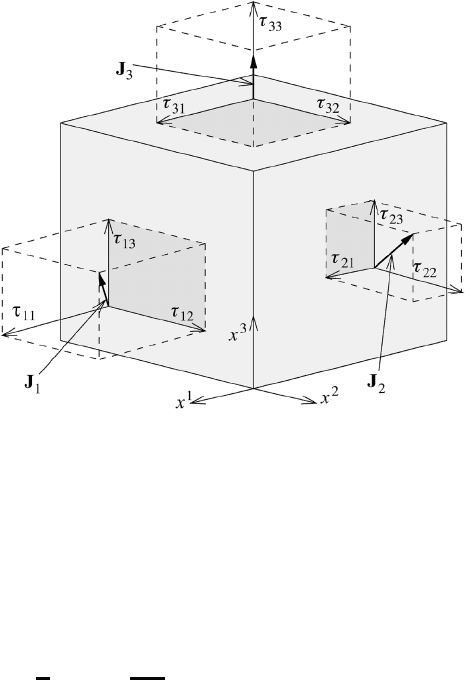
nine possible elements of J acting on the ﬂuid volume element are illustrated in

Figure 5.1.

The row subscript i in the matrix (τ

) refers to the surface element on which

the stress is acting. The column index j refers to the direction of the stress. If

i = j then we are dealing with normal stresses; otherwise (i = j ) with tangential

stresses. The viscous stress vector J

for surfaces i = 1, 2, 3isgivenby

= i

· J = τ

+ τ

(5.4)

Before we focus our attention on equilibrium conditions in the stress ﬁeld, we need

to restate the integral form of the equation of absolute motion,





V (t)

ρv

dτ





V (t)

dτ =



V (t)

ρf

dτ +



S(t)

dS · T

with



S(t)

dS · T =



V (t)

∇·T dτ =



V (t)

(−∇p +∇·J) dτ

(5.5)

This form of the equation of motion will now be used to show that the general and

the viscous stress tensors

T and J are symmetric.

208 The Navier–Stokes stress tensor

Fig. 5.1 Illustration of the viscous stresses acting on a volume element.

5.2 Equilibrium conditions in the stress ﬁeld

We wish to prove the following statement:

Stresses on inﬁnitesimally small ﬂuid volumes must be in equilibrium.

The proof is very brief. We divide (5.5) by the surface S enclosing V and then

implement the following limiting process:

lim

S→0





−



dτ +



ρf

dτ +



dS · T



= 0(5.6)

For easier understanding of the limiting process, let us momentarily think of the

volume as a small cube whose sides have length l. The volume integrals extend

over the volume (l)

while the surface S is proportional to (l)

. By choosing

l arbitrarily small, we ﬁnd that, in the limit l → 0, the numerators of the ﬁrst

two terms go to zero faster than do the denominators. The same type of argument

holds for volumes of any shape, which can always be decomposed into numerous

elementary cubes. Since the ﬁrst two integrals go to zero, we can argue that the

third integral must go to zero also. Therefore, using (5.3), we may also write

lim

S→0



pdS = 0, lim

S→0



dS · J = 0(5.7)

from which we conclude that the total force resulting from all surface forces acting

on the small ﬂuid volume must vanish.

5.3 Symmetry of the stress tensor 209

5.3 Symmetry of the stress tensor

The proof follows from a law of mechanics stating that the individual time derivative

of the angular momentum of the system equals the sum of the moments of the

external forces. First, we observe that





V (t)

r × ρv

dτ





V (t)

r × ρ

dτ (5.8)

where we have used the differentiation rule for ﬂuid volumes. On performing the

vectorial multiplication with the position vector under the integral sign, we ﬁnd

from (5.5)



V (t)

r × ρ

dτ −



V (t)

r × ρf

dτ −



S(t)

r × (dS · T) = 0(5.9)

Next we use Gauss’ divergence theorem, which is also applicable to dyadics. The

third term can then be written as

−



S(t)

r × (dS · T) =



V (t)

∇·(T × r) dτ =



V (t)



∇·

↓

T × r +∇·T ×

↓



dτ



V (t)

(−r ×∇·T − T

) dτ

since ∇·T ×

↓

r = (



T ·∇) × r =



(



T ·∇)r



= (



T · E)

=−T

(5.10)

where T

is the vector of the dyadic T (see also Section M2.4.2). Substitution of

(5.10) into (5.9) yields



V (t)

r ×



− ρf

−∇·T



dτ −



V (t)

dτ = 0(5.11)

The expression in parentheses is actually the equation of absolute motion and must

vanish. Therefore

= 0(5.12)

We already know that the vector of a symmetric dyadic is zero, whereas the vector of

an antisymmetric dyadic differs from zero (see Section M2.4.2). Thus, we conclude

210 The Navier–Stokes stress tensor

that the general stress tensor T is symmetric so that the viscous stress tensor J must

also be symmetric:

J =



J =⇒ n · J =



J · n = J · n (5.13)

This justiﬁes all previous mathematical operations with the stress tensor whenever

we assumed that

J is symmetric.

5.4 The frictional stress tensor and the deformation dyadic

It stands to reason that the motion-dependent frictional force p

)atan

arbitrary point P within the ﬂuid medium cannot result from rigid rotation or from

translation of an entire region surrounding P . The frictional stress is caused only

by deformative velocities in the immediate surrounding of P . Therefore, we should

expect a relation between

J and the deformation dyadic D deﬁned in the previous

chapter. Since the atmosphere may be considered an isotropic medium, we may

deduce that the principal axes of the tensors

J and D coincide. By means of a

suitable rotation of the coordinate system, the so-called principal-axis transforma-

tion (see also Section M2.3), it is possible to reduce the dyadics

J and D to the

simple normal forms

J = τ

+ τ

D = d

+ d

(5.14)

The quantities τ

and d

represent the principal stresses and the relative changes in

length along the orthogonal unit vectors e

deﬁning the directions of the principal

axes. Moreover, the τ

and d

are the eigenvalues of the matrices representing J and

D. Since the matrices are symmetric, the resulting eigenvalues must be real. Next

we need to apply Hooke’s law in the generalized form stating that changes in length

and cross-contractions are proportional to the stresses. Owing to the isotropy of the

medium we may write

(a) τ

= νd

− λ(d

+ d

) = 2µd

− λ(d

+ d

)

(b) τ

= νd

− λ(d

+ d

) = 2µd

− λ(d

+ d

)

= νd

− λ(d

+ d

) = 2µd

− λ(d

+ d

)

(5.15)

where µ = (ν + λ)/2 is known as the molecular coefﬁcient of the deformation

viscosity. The quantities λ and µ are known as Lam

e’s coefﬁcients, and will be

treated here as constants. On multiplying (5.15a) by e

, (5.15b) by e

,and

(5.15c) by e

, and adding the resulting equations, we ﬁnd

J = 2µD − λD

E (5.16)