Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

8.1 Introduction 231
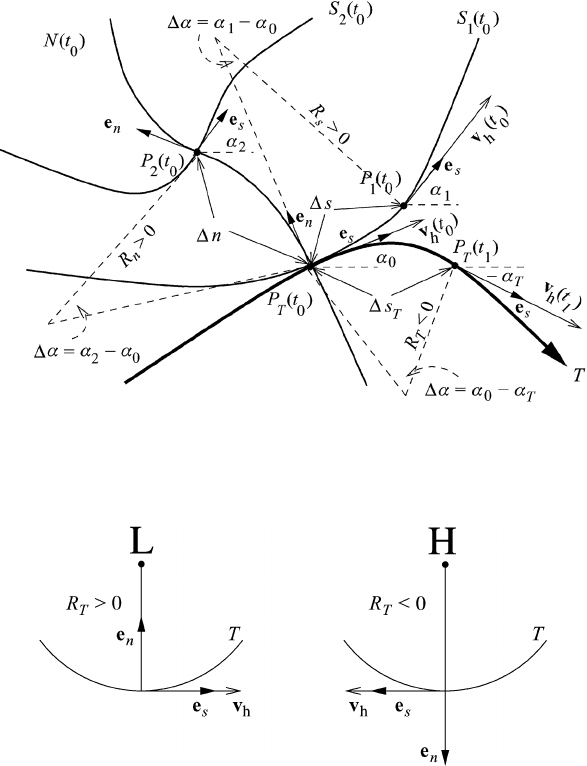
Fig. 8.1 The trajectory T , streamlines S
1
(t
0
),S
2
(t
0
), and normal line N (t
0
).
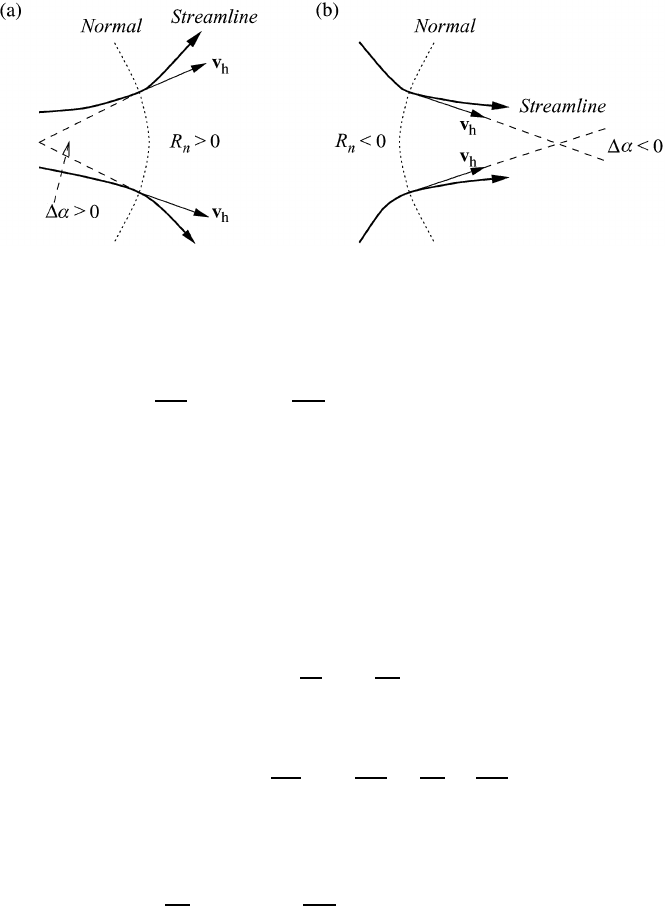
Fig. 8.2 Sign conventions
for the radius of curvature of the trajectory, for t
he northern
hemisphere.
piecewise, the intregability condition is not satisfied, so the order of the partial
derivatives with respect to the independent coordinates cannot be interchanged. In
the next section we will demonstrate this in detail.
Since the curvature may assume either sign, we introduce the generally accepted
convention shown in Figure 8.2. If e
s
is pointing in the counterclockwise direction
(rotation in the positive sense) the radius of curvature of the trajectory R
T
is taken
as positive. If the motion is in the clockwise direction R
T
is negative.
232 Natural coordinates
8.2 Differential definitions of the coordinate lines
The natural coordinate system is defined by the orthogonal vector basis (e
s
, e
n
, e
z
),
where e
s
defines the direction of motion of a particle so that e
s
×e
n
= e
z
. Therefore,
the horizontal velocity is given by
v
h
= iu + jv = i
|
v
h
|
cos α + j
|
v
h
|
sin α = e
s
|
v
h
|
= e
s
v
*
h
(8.3)
where v
*
h
is the physical measure number of the horizontal velocity. Differentials
of the coordinate lines are defined by
dq
*
1
= ds = R
s
dα, dq
*
2
= dn = R
n
dα, dq
*
3
= dz (8.4)
Here dq
*
1
and dq
*
2
are the elements of arclength of the streamline and of the normal,
while dq
*
3
is the line element along e
z
.
Before proceeding, we need to state the transformation relationships between
the Cartesian and the natural coordinate system. At time t = constant these simply
correspond to the rotation of the Cartesian system about the vertical axis by the
angle α counterclockwise. Let the orthogonal transformation matrix be denoted by
T
ij
=
cos α −sin α 0
sin α cos α 0
001
(8.5)
Then
i
j
k
=
T
ij
e
s
e
n
e
z
,
e
s
e
n
e
z
=
T
ij
i
j
k
(8.6)
1
The variation of the second expression of (8.6) is given by
δ
e
s
e
n
e
z
=
δ
T
ij
T
ij
e
s
e
n
e
z
=
0
δα 0
−
δα 00
000
e
s
e
n
e
z
=
δα
e
n
−e
s
0
(8.7)
or, in component form, by
δe
s
= e
n
δα, δe
n
=−e
s
δα, δe
z
= 0(8.8)
1
The tilde denotes the transpose of (T
ij
).
8.2 Differential definitions of the coordinate lines 233
The operator δ takes the place of all differential operators such as d/dt,∂/∂t,d/ds,
and ∂/∂s. However, the budget operator D/Dt is not included in this group.
Therefore, we may write
(a)
de
s
dt
= e
n
dα
dt
,
de
n
dt
=−e
s
dα
dt
(b)
de
s
ds
T
= e
n
dα
ds
T
=
e
n
R
T
,
de
n
ds
T
=−e
s
dα
ds
T
=−
e
s
R
T
(c)
∂e
s
∂t
s,n,z
= e
n
∂α
∂t
s,n,z
,
∂e
n
∂t
s,n,z
=−e
s
∂α
∂t
s,n,z
(d)
∂e
s
∂n
= e
n
∂α
∂n
=
e
n
R
n
,
∂e
n
∂n
=−e
s
∂α
∂n
=−
e
s
R
n
(e)
∂e
s
∂s
= e
n
∂α
∂s
=
e
n
R
s
,
∂e
n
∂s
=−e
s
∂α
∂s
=−
e
s
R
s
(8.9)
For convenience, in parts (d) and (e) we have not explicitly stated the variables
to be held constant. These are the famous Frenet–Serret formulas for the two-
dimensional situation. A detailed discussion of the three-dimensional case, for
example, may be found in Lass (1950). We conclude this section by stating the
gradient operator in the natural coordinate system:
∇ψ = q
n
∂ψ
∂q
n
= e
s
∂ψ
∂s
+ e
n
∂ψ
∂n
+ e
z
∂ψ
∂z
(8.10)
where ψ is some arbitrary but well-defined field function. Application of (8.3) to
(8.10) results in the advection term
v
h
·∇ψ = v
*
h
∂ψ
∂s
(8.11)
which will be needed later.
As we have stated above, the order of the partial derivatives with respect to the
independent variables s and n cannot be interchanged. We will prove this now.
Since the partial derivatives transform in the same way as the corresponding unit
234 Natural coordinates
vectors, we may write from (8.6)
(a)
∂
∂s
∂
∂n
∂
∂z
=
T
ij
∂
∂x
∂
∂y
∂
∂z
(b)
∂
∂x
∂
∂y
∂
∂z
=
T
ij
∂
∂s
∂
∂n
∂
∂z
(8.12)
Application of (8.12a) to the arbitrary field function ψ yields
∂ψ
∂s
= cos α
∂ψ
∂x
+ sin α
∂ψ
∂y
(8.13)
Taking the partial derivative with respect to time, we obtain
∂
2
ψ
∂t ∂s
=−sin α
∂α
∂t
∂ψ
∂x
+ cos α
∂
2
ψ
∂t ∂x
+ cos α
∂α
∂t
∂ψ
∂y
+ sin α
∂
2
ψ
∂t ∂y
(8.14a)
The order of partial differentiation with respect to (t,x)and(t,y) may be inter-
changed so that
∂
2
ψ
∂t ∂s
=−sin α
∂α
∂t
∂ψ
∂x
+ cos α
∂
2
ψ
∂x ∂t
+ cos α
∂α
∂t
∂ψ
∂y
+ sin α
∂
2
ψ
∂y ∂t
(8.14b)
Using the above transformation rule (8.12b), we find from (8.14b)
∂
2
ψ
∂t ∂s
=
∂α
∂t
∂ψ
∂n
+
∂
2
ψ
∂s ∂t
(8.14c)
which is clearly showing that the mixed partial derivatives are not identical. For
the remaining partial derivatives of the natural coordinates analogous expressions
8.3 Metric relationships 235
may be derived. All transformation rules are summarized in
∂
2
ψ
∂t ∂s
=
∂α
∂t
∂ψ
∂n
+
∂
2
ψ
∂s ∂t
∂
2
ψ
∂z∂s
=
∂α
∂z
∂ψ
∂n
+
∂
2
ψ
∂s ∂z
∂
2
ψ
∂t ∂n
=−
∂α
∂t
∂ψ
∂s
+
∂
2
ψ
∂n∂t
∂
2
ψ
∂z∂n
=−
∂α
∂z
∂ψ
∂s
+
∂
2
ψ
∂n∂z
∂
2
ψ
∂n∂s
=
∂α
∂s
∂ψ
∂s
+
∂α
∂n
∂ψ
∂n
+
∂
2
ψ
∂s ∂n
∂
2
ψ
∂z∂t
=
∂
2
ψ
∂t ∂z
(8.15)
The derivation of the second from last expression is a little tricky. We take the
partial derivative of the field function ψ first with respect to s andthenwithrespect
to n. Next we reverse the order of differentiation and then combine the resulting
equations.
8.3 Metric relationships
The metric coefficients of the orthogonal natural coordinate system are obtained
from the fundamental metric form
(dr)
2
= g
nn
(dq
n
)
2
= (ds)
2
+ (dn)
2
+ (dz)
2
= R
2
s
(dα)
2
+ R
2
n
(dα)
2
+ (dz)
2
(8.16)
Comparison of coefficients gives immediately
g
11
= R
2
s
,g
22
= R
2
n
,g
33
= 1(8.17)
The functional determinant then follows directly as
√
g =
g
ij
= R
s
R
n
(8.18)
We know from Chapter M1 that, in orthonormal systems such as the natural co-
ordinate system of the tangential plane, there is no difference between covariant
and contravariant unit vectors and the corresponding physical measure numbers.
The covariant and contravariant basis vectors, however, differ and can be easily
formulated with the help of (8.17).
236 Natural coordinates
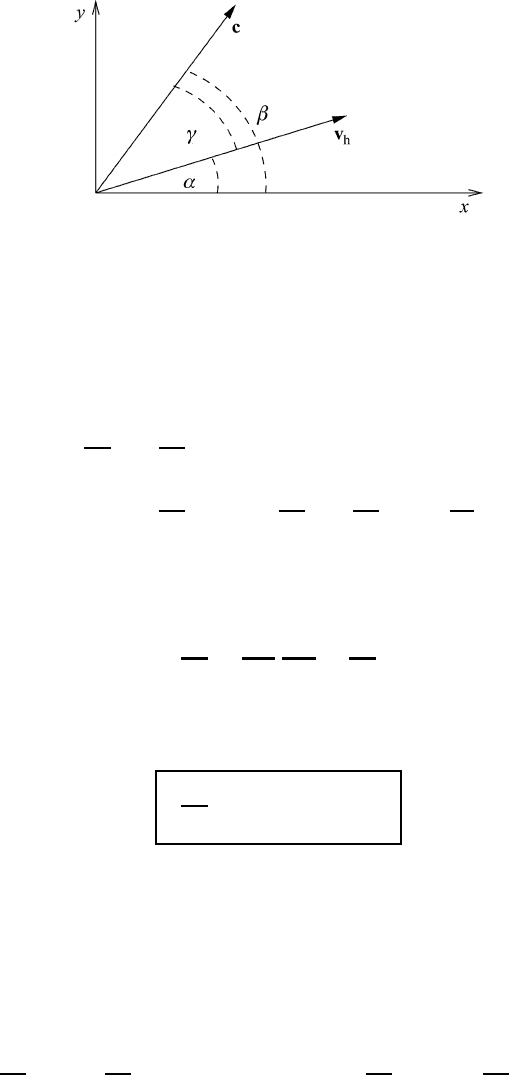
Fig. 8.3 Definitions of angles appearing in equation (8.23).
8.4 Blaton’s equation
Blaton’s equation gives a relation between the radii of curvature of the streamline
and the trajectory. The Euler development of the contingency angle α gives
dα
dt
=
∂α
∂t
n,s,z
+ v
h
·∇α
=
∂α
∂t
n,s,z
+ v
*
h
∂α
∂s
=
∂α
∂t
n,s,z
+
v
*
h
R
s
(8.19)
where use has been made of equations (8.2) and (8.11). By writing dα/dt as
dα
dt
=
dα
ds
T
ds
T
dt
=
v
*
h
R
T
(8.20)
we find the desired result
∂α
∂t
n,s,z
= v
*
h
(K
T
− K
s
)
(8.21)
The quantities K
T
= 1/R
T
and K
s
= 1/R
s
are the curvatures of the trajectory and
the streamline. In case of directional stationarity Blaton’s equation (8.21) reduces
to K
T
= K
s
.
It might be instructive to apply (8.21) to the case of a nondeveloping field moving
with the phase speed c. From (7.37) and with reference to Figure 8.3 we obtain
∂α
∂t
x,y
=
∂α
∂t
x
,y
− c ·∇α =−c cos β
∂α
∂x
− c sin β
∂α
∂y
(8.22a)
8.4 Blaton’s equation 237
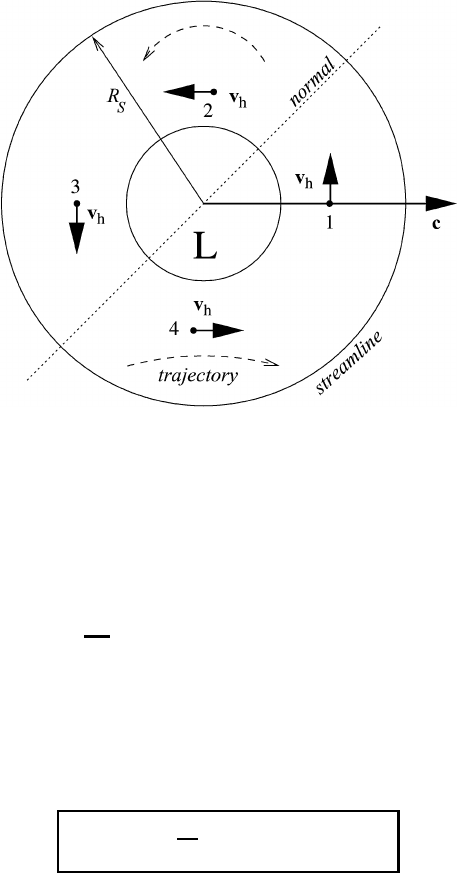
Fig. 8.4 Curvatures of the trajectory at various points within a speedily moving circular
cyclone.
The local time derivative at constant x
,y
vanishes due to the assumed stationarity.
Using (8.12b) to replace ∂α/∂x and ∂α/∂y in terms of ∂α/∂s = K
s
and ∂α/∂n =
K
n
we obtain
∂α
∂t
n,s
=−c(K
s
cos γ + K
n
sin γ )(8.22b)
where K
n
= 1/R
n
is the curvature of the normal. The relation between α, β and
the angle γ , as defined in Figure 8.3. is found from the addition theorems of the
trigonometric functions. Combining (8.21) and (8.22b) finally gives
K
T
= K
s
−
c
v
*
h
(K
s
cos γ + K
n
sin γ )
(8.23)
We will conclude this section by applying (8.23) to the situation of a speedily
moving cyclone for which c/v
*
h
> 1. Figure 8.4 demonstrates the situation.
Obviously, the curvature K
n
of the normal is zero. The curvature K
s
of the
low-pressure system L is positive by convention. The curvature of the trajectory
K
T
and its sign may then be easily found from (8.23). At points 1 (γ = 90
◦
)
and3(γ = 270
◦
) the curvatures of the trajectory and the streamline coincide,
i.e. K
T
= K
s
. At point 2 (γ = 180
◦
) the curvature of the trajectory K
T
exceeds the
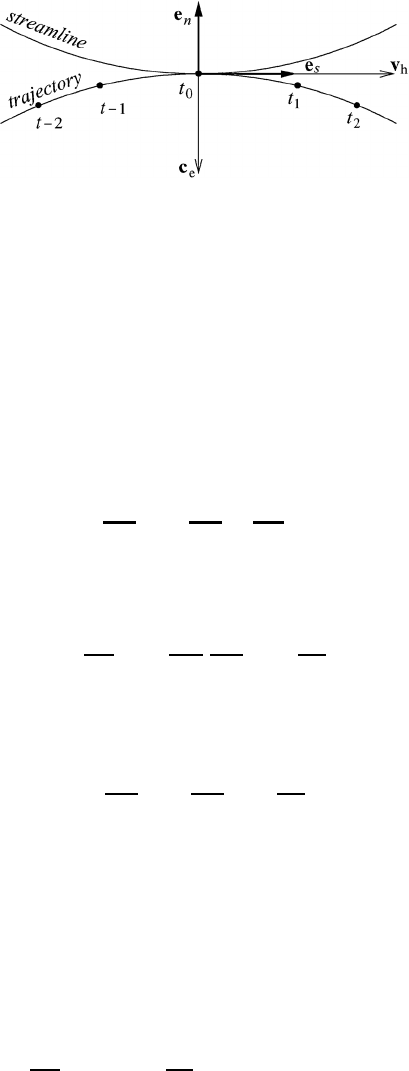
238 Natural coordinates
Fig. 8.5 Tangential and centripetal acceleration.
cyclonic curvature of the streamline K
s
, whereas at point 4 (γ = 0
◦
) the curvature
of the trajectory is anticyclonic, that is K
T
< 0. For an additional discussion of this
topic see, for example, Petterssen (1956).
8.5 Individual and local time derivatives of the velocity
The individual derivative of (8.3) gives
dv
h
dt
= e
s
dv
*
h
dt
+
de
s
dt
v
*
h
(8.24)
From (8.9) and (8.2) we find
de
s
dt
= e
n
dα
ds
T
ds
T
dt
= e
n
v
*
h
R
T
(8.25)
Substitution of (8.25) into (8.24) results in
dv
h
dt
= e
s
dv
*
h
dt
+ e
n
v
*
2
h
R
T
(8.26)
The first term on the right-hand side of (8.26) has the direction of v
h
and is known
as the tangential acceleration. The second term has a direction perpendicular to
v
h
and represents the centripetal acceleration c
e
which is acting on an air particle
whenever the trajectory is not straight-line flow; see Figure 8.5.
We proceed similarly with the partial time derivative of the velocity. From (8.9c)
and with the help of Blaton’s equation (8.21) we first obtain
∂e
s
∂t
n,s,z
= e
n
∂α
∂t
n,s,z
= e
n
v
*
h
(K
T
− K
s
)(8.27)
8.6 Differential invariants 239
Fig. 8.6 Regions of (a) diffluence and (b) confluence.
Using this equation, we find from (8.3) for the local time change in the natural
coordinate system the expression
∂v
h
∂t
n,s,z
= e
s
∂v
*
h
∂t
n,s,z
+ e
n
v
*
2
h
(K
T
− K
s
)(8.28)
which is needed whenever the Euler expansion is required.
8.6 Differential invariants
8.6.1 The horizontal divergence of the velocity
The starting point of the derivation is the development of ∇·v
h
in the natural
coordinate system:
∇·v
h
=
e
s
∂
∂s
+ e
n
∂
∂n
· (e
s
v
*
h
)(8.29)
Since this system is orthonormal, one immediately obtains
∇·v
h
= e
n
·
∂e
s
∂n
v
*
h
+
∂v
*
h
∂s
=
v
*
h
R
n
+
∂v
*
h
∂s
(8.30)
where (8.9d) and (8.9e) have been used to evaluate the partial derivatives. The
following abbreviations are introduced:
D
d
=
v
*
h
R
n
,D
v
=
∂v
*
h
∂s
=⇒ ∇ · v
h
= D
d
+ D
v
(8.31)
The part D
d
is known as the divergence due to directional change while D
v
refers
to the velocity divergence. The physical interpretation of (8.31) follows from
Figure 8.6 showing regions of diffluence and confluence as well as the sign
convention for the radius of curvature of the normal. In the region of diffluence
the curvature is positive in the mathematical sense so that R
n
> 0, whereas in the
region of confluence the curvature of the normal is negative or R
n
< 0.

240 Natural coordinates
Fig. 8.7 A region of diffluence in the atmosphere, showing both parts of the divergence
with D
d
> 0andD
v
< 0.
In large-scale atmospheric motion the horizontal divergence is very small and
of the order of
|
∇·v
h
|
= 10
−5
–10
−6
s
−1
. This results from the fact that
|
∇·v
h
|
,in
general, is composed of the two parts D
d
and D
v
which nearly compensate each
other. Therefore, it is very difficult to measure the horizontal velocity divergence.
The idea is demonstrated in Figure 8.7.
8.6.2 Vorticity or the vertical component of ∇×v
h
The concept of vorticity is very important in meteorology since the vorticity is a
measure of rotation. Here we will only briefly dwell on this subject, but in later
chapters we will exploit it fully since it is closely related to atmospheric circulation.
In the natural coordinate system the components of ∇×v
h
are given by
∇×v
h
=
e
s
∂
∂s
+ e
n
∂
∂n
× (e
s
v
*
h
) = e
s
×
∂e
s
∂s
v
*
h
+ e
n
× e
s
∂v
*
h
∂n
(8.32)
where use has been made of equations (8.9d) and (8.9e). The vertical component
of this expression is then
ζ = e
z
·∇×v
h
=
v
*
h
R
s
−
∂v
*
h
∂n
(8.33)
where again (8.9d) has been utilized. The vorticity ζ consists of two parts, caused
by the curvature of the streamlines ζ
c
and the velocity shear ζ
s
.
ζ = ζ
c
+ ζ
s
=
v
*
h
R
s
−
∂v
*
h
∂n
(8.34)
As has already been mentioned, in the northern hemisphere the radius of curvature
of the streamlines R
s
is defined to be positive for cyclonic flow so that R
s
> 0,
