Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


9.3 Particle invariance at boundary surfaces, displacement velocities 251
9.3 Particle invariance at boundary surfaces, displacement velocities
The assumption of particle invariance at a boundary surface implies that the DS
is composed of the same group of particles for as long as it exists. If a particle is
a part of the DS it has to remain in the DS; it cannot penetrate the surface. Thus,
the DS is a material or fluid surface: see also Section M6.4. Otherwise the particle
would experience an infinitely large variation of its scalar value, say T > 0, so
that T /h →∞. In order to realize the assumption of particle invariance, the
normal velocity on both sides of the DS must be the same, i.e. v
(1)
· e
n
= v
(2)
· e
n
.
Let us consider a DS defined by
z = z
DS
(x,y, t)(9.17)
The function
F (x,y,z, t) = z − z
DS
(x,y, t) = 0(9.18)
may be considered to be the defining equation of the DS. Since all particles of the
DS must remain within the DS, we may write the condition of particle invariance
as
F = 0,
dF
dt
= 0 =⇒
dF
dt
(i)
=
∂F
∂t
+ v
(i)
·∇F =
∂F
∂t
+ v
(i)
· e
n
|
∇F
|
= 0,i= 1, 2
(9.19)
The last expression follows from the fact that ∇F is perpendicular to the DS. By
evaluating (9.19) for i = 1andi = 2 and subtracting one of the results from the
other we again obtain (9.10).
The displacement velocity c of the DS and the unit normal e
n
to the DS are
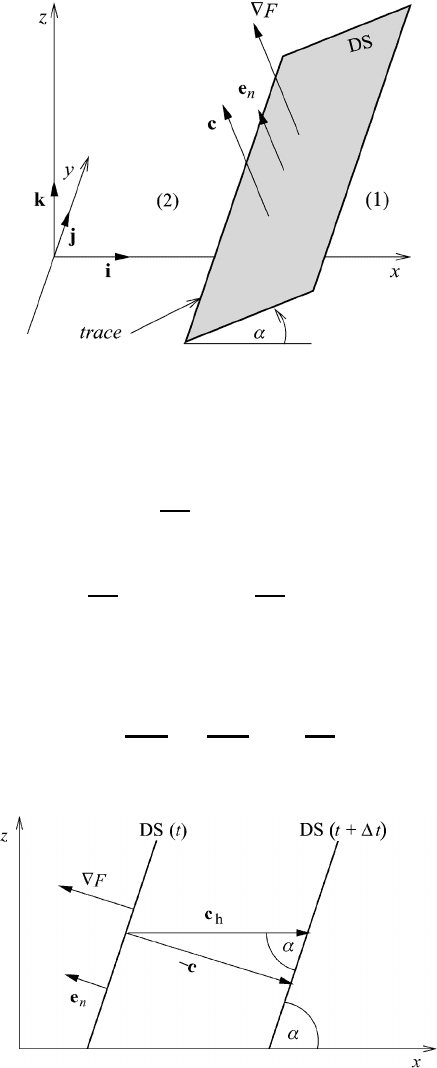
considered positive if they are pointing from side (1) to (2); see Figure 9.7. In
order to keep the mathematical analysis as simple as possible, we have arranged
the coordinate system in such a way that the trace of the DS (front) is parallel to the
y-axis. The unit vector i which is perpendicular to the trace of the DS is pointing
in the direction of the rising boundary surface. The angle α defines the inclination
of the DS.
The relation between the unit vector e
n
and the Cartesian vectors i and k is easily
found from
e
n
= e
n
· E = e
n
· ii + e
n
· jj + e
n
· kk =−sin α i + cos α k (9.20)
Owing to the particle invariance, the displacement velocity c = ce
n
of the DS must
be equal to the normal component of the wind velocity
c = (v
(i)
· e
n
)e
n
= (−u
(i)
sin α + w
(i)
cos α)e
n
= ce
n
,i= 1, 2
(9.21)
252 Boundary surfaces and boundary conditions
Fig. 9.7 The orientation of the discontinuity surface.
Moreover, the displacement velocity c can also be expressed by means of the
particle invariance. From (9.19) we find
v
(i)
· e
n
=−
∂F
∂t
|
∇F
|
−1
,i= 1, 2(9.22)
so that the displacement velocity is also given by
c =−
∂F
∂t
|
∇F
|
−1
e
n
=−
∂F
∂t
(e
n
·∇F )
−1
e
n
(9.23)
Of greater interest than the displacement velocity c itself is the horizontal dis-
placement velocity c
h
shown in Figure 9.8. From the figure and from (9.23) we find
for the horizontal displacement the relation
c
h
= c
h
i =−
c
sin α
i =
c
i · e
n
i =−
∂F
∂t
(i ·∇F )
−1
i (9.24)
Fig. 9.8 The horizontal displacement velocity.
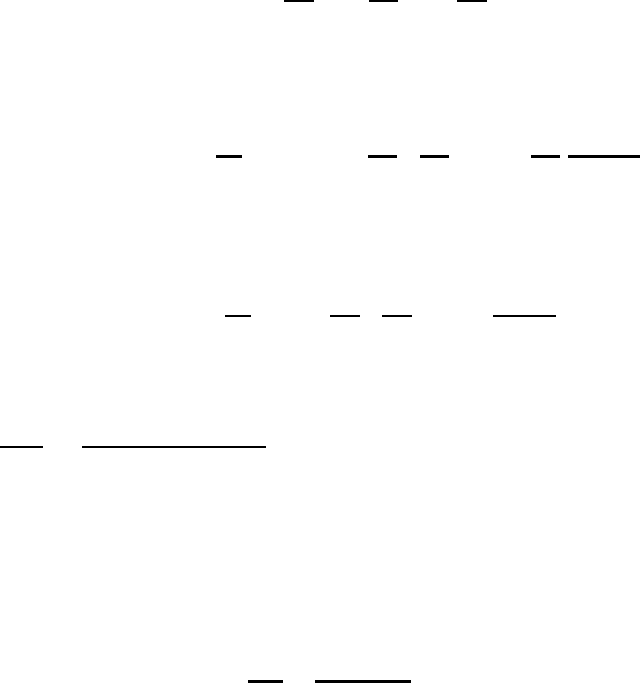
9.4 The kinematic boundary-surface condition 253
where the measure number c
h
can have either sign. Owing to the special orientation
of the coordinate system, the same result also follows on expanding the equation
of particle invariance:
F = 0,dF= 0 =
∂F
∂t
dt +
∂F
∂x
dx +
∂F
∂z
dz (9.25)
Application of this equation for z = constant yields the horizontal displacement
velocity
F = 0,z= constant:
dx
dt
DS
= c
h
=−
∂F
∂t
∂F
∂x
−1
=−
∂F
∂t
1
(i ·∇F )
(9.26)
which is identical with (9.24). From (9.25) we also find the inclination of the DS:
F = 0,t= constant:
dz
dx
DS
=−
∂F
∂x
∂F
∂z
−1
=−
i ·∇F
k ·∇F
= tan α
(9.27)
On substituting (9.21) into (9.24) we find the useful expression
c
h
=−
c
sin α
i =
u
(i)
sin α − w
(i)
cos α
sin α
i = (u
(i)
− w
(i)
cot α)i,i= 1, 2(9.28)
This equation states that, for equal conditions regarding u and w, a steep DS (cot α
is small) moves faster than does a DS with a shallow inclination. A slope of a
frontal surface of 1: 50 is considered steep whereas 1: 300 is regarded as slight. By
expressing (9.28) for i = 1andi = 2, upon subtraction of one equation from the
other we find another expression for the inclination of the DS:
tan α =
{
w
}
{
u
}
=
w
(2)
− w
(1)
u
(2)
− u
(1)
(9.29)
involving the discontinuity jump of the velocity components.
9.4 The kinematic boundary-surface condition
There are various types of boundary surface. It is necessary to make a distinction
between outer or external and internal boundary surfaces. An external boundary
surface, for example, is the surface of the earth for which a lower boundary condi-
tion must be formulated. An internal boundary surface is an imagined separation
boundary between two fluids of differing densities.
254 Boundary surfaces and boundary conditions
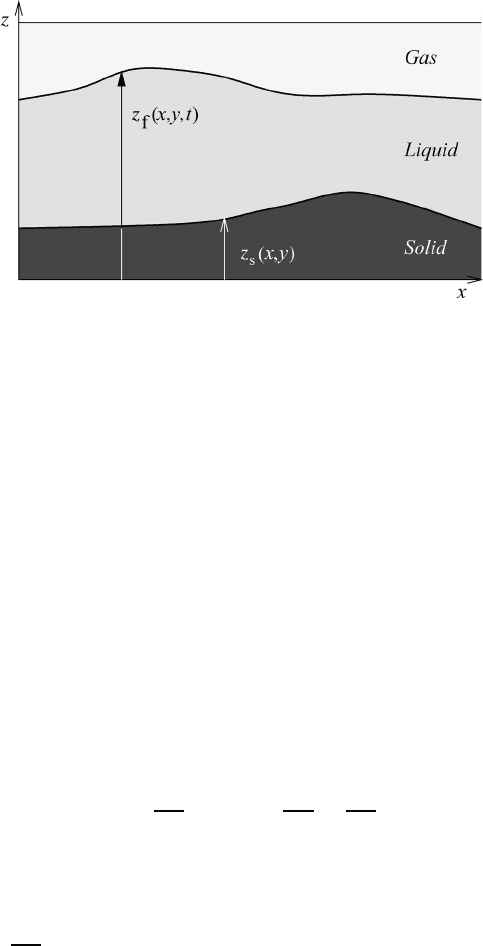
Fig. 9.9 External boundary surfaces.
9.4.1 External boundary surfaces
Let us consider an ideal frictionless fluid whose so-called free surface z
f
is separat-
ing the fluid from a vacuum or a gas-filled space. To a good approximation this is
realized by the boundary separating the ocean and the atmosphere. While the free
surface is time-dependent, a time-independent surface such as the surface of the
earth is considered to be a rigid wall z
s
, see Figure 9.9. Therefore, the boundary
equations may be written as
F (x,y,z, t) = z − z
f
(x,y, t) = 0,F(x,y,z) = z − z
s
(x,y) = 0(9.30)
As has already been mentioned, any boundary surface, as long as it exists, is
considered to be particle-invariant, meaning that the boundary surface is always
made up of the same group of particles. From (9.30) follows the so-called kinematic
boundary-surface condition. For the nonstationary free surface we may write
Free surface: F = 0,
∂F
∂t
= 0,
dF
dt
=
∂F
∂t
+v·e
n
|
∇F
|
= 0(9.31)
where the velocity refers to the fluid medium. With the help of (9.23) this formula
can be rewritten as
F = 0,
∂F
∂t
|
∇F
|
−1
+ v · e
n
=−c + e
n
· v =−e
n
· e
n
c + e
n
· v = 0(9.32)
or by means of
F = 0, e
n
· (v − c) = 0(9.33)
Since the unit vector e
n
is oriented normal to the DS, the vector v −c, representing
the velocity difference, must lie in the DS.

9.4 The kinematic boundary-surface condition 255
For a rigid surface we find analogously
Rigid surface: F = 0.
∂F
∂t
= 0,
dF
dt
= 0, v ·e
n
= 0(9.34)
so that the velocity vector itself lies in the DS.
In a viscous fluid not only does the normal component of the velocity vanish at
a rigid wall as implied by (9.34) but also the tangential component must vanish. In
this more realistic case the kinematic boundary-surface condition must be written
as
F = 0, v = 0(9.35)
9.4.2 Internal boundary surfaces
Let us consider an internal DS between two frictionless fluids such as a tempera-
ture DS of order zero. We again start our analysis from the condition of particle
invariance (9.19) which may also be written as
∂F
∂t
|
∇F
|
−1
e
n
· e
n
+ v
(i)
· e
n
= 0,i= 1, 2(9.36a)
Scalar multiplication of (9.23) by e
n
and substitution of the result into (9.36a) gives
e
n
· (v
(i)
− c) = (−u
(i)
sin α + w
(i)
cos α) − c = 0,i= 1, 2(9.36b)
where we have used the orientation of the coordinate system shown in Figure 9.7.
Setting in succession in (9.36a) i = 1, 2 and subtracting one of the results from the
other yields the kinematic boundary-surface condition for the internal DS:
F = 0,
∂F
∂t
= 0:
(a)
{
v
}
·∇F = 0
(b)
{
v
}
· e
n
=·v = 0
(c) w
(2)
− w
(1)
= (u
(2)
− u
(1)
)tanα or
{
w
}
/
{
u
}
= tan α
(9.37)
Equations (9.37b) and (9.37c) follow directly from (9.37a) since
|
∇F
|
= 0.
In (9.37b) we have also used the definition (9.8) for the surface divergence.
Again, we have obtained equation (9.29) giving the inclination of the discontinuity
surface.
Equations (9.37a) and (9.37b) require that the velocity-jump vector
{
v
}
at the
zeroth-order DS must be tangential to the DS while the normal component of v
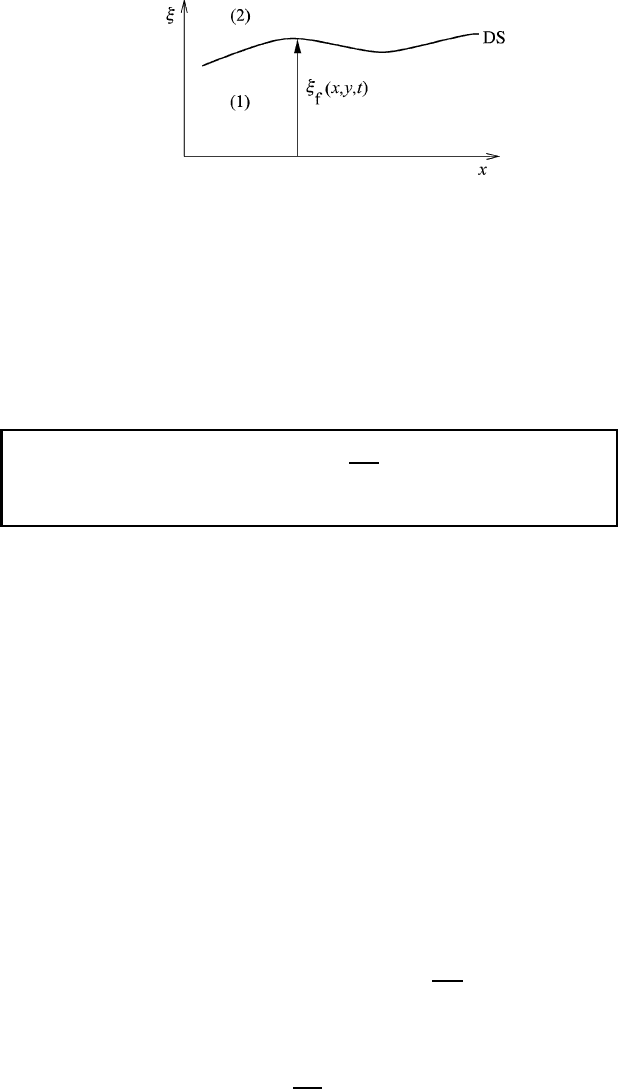
256 Boundary surfaces and boundary conditions
Fig. 9.10 The generalized height of a discontinuity surface.
must be identical on both sides of the DS. The component form (9.37c) of the
kinematic boundary-surface condition gives a relation between the slope tan α and
the velocity jumps of the components of the wind velocity.
Equation (9.37) is valid for a nonstationary (∂F/∂t = 0) internal boundary
surface. For a stationary boundary surface (∂F/∂t = 0) the kinematic boundary-
surface condition reduces to
F = 0,
∂F
∂t
= 0:
v
(i)
·∇F = 0, v
(i)
· e
n
= 0, tan α = w
(i)
/u
(i)
,i= 1, 2
(9.38)
9.4.3 The generalized vertical velocity at boundary surfaces
The condition of particle invariance can be used to derive the vertical velocity
at outer and internal boundary surfaces. We will first introduce the generalized
vertical coordinate which will also be of importance in our future work when we
consider the atmospheric motion in arbitrary coordinate systems; see Figure 9.10.
As specific examples of the generalized vertical coordinates we consider the
atmospheric pressure p and the height z of a pressure surface which generally
depend on the horizontal coordinates x and y. Therefore, we may write
p = p
f
(x,y, t) =⇒ p − p
f
(x,y, t) = F
1
(x,y, p, t) = 0
z = z
f
(x,y, t) =⇒ z − z
f
(x,y, t) = F
2
(x,y, z,t) = 0
(9.39)
or, in general,
F = ξ − ξ
f
(x,y, t) = 0,
dF
dt
= 0(9.40)
Individual differentiation with respect to time gives
F = 0,
˙
ξ
(i)
=
∂ξ
f
∂t
+ v
(i)
h
·∇
h
ξ
f
,i= 1, 2(9.41)
9.4 The kinematic boundary-surface condition 257
which is the generalized velocity at the boundary surface. If we are dealing with an
outer stationary or nonstationary boundary surface then (9.41) refers to the interior
fluid. Writing (9.41) down for both sides of the DS (i = 1, 2) and subtraction of
one of the results from the other gives
F = 0,
{
˙
ξ
}
=
{
v
h
}
·∇
h
ξ
f
(9.42)
This equation is equivalent to the kinematic boundary-surface condition since it
reduces to (9.37a) if the y-axis is taken along the trace of the discontinuity surface.
Let us now consider various cases of (9.41) and (9.42), which are collected in the
following equations.
(I) ξ = z,
˙
ξ = w
The horizontal surface of the earth: z
s
= constant
∂z
s
∂t
= 0, ∇
h
z
s
= 0,w
s
= 0(9.43a)
Earth’s surface with topography: z
s
= z
s
(x,y)
∂z
s
∂t
= 0, ∇
h
z
s
= 0,w
s
= v
s
·∇
h
z
s
(9.43b)
A free nonstationary surface: ξ
f
= H
w
H
=
∂H
∂t
+ v
h
·∇
h
H (9.43c)
A nonstationary internal DS:
w
(2)
f
− w
(1)
f
= (v
(2)
h
− v
(1)
h
) ·∇
h
z
f
(9.43d)
A stationary internal DS:
w
(i)
f
= v
(i)
h
·∇
h
z
f
,i= 1, 2(9.43e)
(II) ξ =−p,
˙
ξ =−˙p =−ω
A nonstationary internal DS:
ω
(2)
f
− ω
(1)
f
= (v
(2)
− v
(1)
) ·∇
h
p
f
(9.43f)
A stationary internal DS:
ω
(i)
f
= v
(i)
h
·∇
h
p
f
,i= 1, 2(9.43g)
These expressions do not require additional explanations.

258 Boundary surfaces and boundary conditions
Fig. 9.11 The pressure-gradient jump at a vertical (left) and a horizontal (right) cross-
section of a pressure-discontinuity surface. ∇
v
= i ∂/∂x + k ∂/∂z.
9.5 The dynamic boundary-surface condition
At a boundary surface the stress tensor T as defined in (5.3) must be continuous,
otherwise infinitely large pressure gradients would result. This physical condition
is known as the dynamic boundary-surface condition, which can be written as
(a) {
T}=0
(b)
{
p
}
= 0
(c) p = 0,
dp
dt
= 0
(9.44)
Equation (9.44a) is the general condition for viscous fluids whereas (9.44b) refers
to frictionless fluids. This condition states that the pressure boundary surface must
be a DS of first order at least. If we consider the upper boundary of the atmosphere
as a free material surface then condition (9.44c) must apply. With reference to
equations (9.14) and (9.16) we may write
×∇p = e
n
×
{
∇p
}
= 0,dr ·
{
∇p
}
= 0(9.45)
where dr lies in the DS. Equation (9.45) shows that, in a frictionless fluid, the jump
of the pressure gradient at a first-order DS relative to p must be perpendicular to the
DS. The pressure itself, however, is continuous as stated by (9.44b). The situation
is demonstrated in Figure 9.11.
Finally, we may combine the kinematic and the dynamic boundary-surface con-
ditions to give the so-called mixed boundary-surface condition for frictionless
fluids by setting in (9.30)
F (x,y,z, t) = p
(2)
(x,y, z,t) − p
(1)
(x,y, z,t) =
{
p
}
= 0(9.46)
The result is
∂p
∂t
+ v
(i)
·
{
∇p
}
= 0,i= 1, 2(9.47)

9.6 The zeroth-order discontinuity surface 259
On writing this expression down for both sides of the boundary surface and sub-
tracting one of the results from the other we obtain
{
v
}
·
{
∇p
}
= 0
(9.48)
Since
{
∇p
}
= 0 by assumption, we find that, in a frictionless fluid, the velocity
jump must be perpendicular to the jump of the pressure gradient.
9.6 The zeroth-order discontinuity surface
9.6.1 The inclination of the zeroth-order DS
We wish to treat briefly the inclination of a zeroth-order DS in a frictionless fluid
for various conditions. In our example we consider a boundary surface separating
two air masses of different densities. Using the ideal-gas law and recalling that
{
p
}
= 0 at the DS, it is easy to show that this corresponds to a zeroth-order DS of
the virtual temperature T
v
or
{
ρ
}
=−
{
T
v
}
p/(R
0
T
(1)
v
T
(2)
v
)(9.49)
It stands to reason that, for air masses at rest, the DS must be horizontal, with
the warmer lighter air on top of the colder denser air. There can be no equilibrium
between two air masses of different densities seperated by a vertical DS. If the air
masses are in motion the colder air will form a wedge under the warmer air. It
is important to realize that both the kinematic and the dynamic boundary-surface
conditions must be satisfied at the DS. We repeat the dynamic boundary condition
(9.45) and write
{
∇p
}
· dr =
{
∇
v
p
}
· dr =
{
∇
v
p
}
· i dx +
∂p
∂z
dz = 0
with ∇
v
= i
∂
∂x
+ k
∂
∂z
(9.50)
Again we have used the special arrangement of the coordinate system. From this
equation we obtain the inclination of the DS, which is given by
tan α =
dz
dx
DS
= i ·∇
v
z
DS
=−i ·
{
∇
v
p
}
∂p
∂z
−1
(9.51a)
or by
∇
v
z
DS
=
∇
v
p
(1)
−∇
v
p
(2)
∂p
(2)
∂z
−
∂p
(1)
∂z
−1
(9.51b)
260 Boundary surfaces and boundary conditions
Assuming the validity of the hydrostastic equation for the present situation, we
may rewrite (9.51b) and obtain an equivalent expression for the slope of the DS:
∇
v
z
DS
=
{
∇
v
p
}
g
{
ρ
}
=
∇
v
p
(2)
−∇
v
p
(1)
g(ρ
(2)
− ρ
(1)
)
or tan α =
i ·
{
∇
v
p
}
g
{
ρ
}
(9.52)
Owing to the choice of the coordinate system, see Figure 9.7, the slope is always
greater than zero, or tan α>0. Furthermore, we assume that we have stable atmos-
pheric conditions in the sense that the denser colder air is located below the lighter
warmer air. We note that the denominator in (9.52) is smaller than zero, so the
numerator must be negative in order to make the fraction positive. We will use this
information by considering the surface divergence of ∇p:
·∇p = e
n
·
{
∇p
}
= (−sin α i + cos α k) ·
∇
h
p + k
∂p
∂z
(9.53)
where we have replaced the unit normal e
n
by means of (9.20). On carrying out the
scalar multiplication, we obtain the equivalent expression
·∇p =−i ·
{
∇
h
p
}
sin α +
∂p
∂z
cos α>0
since i ·
{
∇
v
p
}
= i ·
{
∇
h
p
}
< 0and
∂p
∂z
= g
ρ
(1)
− ρ
(2)
> 0
(9.54)
See Figure 9.11. Since both the horizontal and the vertical parts of (9.54) are larger
than zero, we find for reasons of stability that the total surface divergence of the
pressure gradient must also be larger than zero. As shown in the left-hand panel of
Figure 9.12, in general this is possible only in case of a cyclonic pressure-gradient
jump (cyclonic air motion). Otherwise the horizontal part of the surface divergence
would not be positive. The anticyclonic pressure-gradient jump would violate the
requirement that the first term of (9.54) must be greater than zero; see the right-hand
panel of Figure 9.12.
We are now ready to find an expression for the inclination of the DS in the
presence of a geostrophic wind field.
9.6.2 A discontinuity surface of zeroth-order in the geostrophic wind field
This type of discontinuity surface is also known as the Margules boundary surface.
To obtain a suitable expression for the pressure-gradient jump at the DS, we use
the approximate form of the equation of motion
ρ
dv
h
dt
+ ρf k × v
h
+ ρgk =−∇
h
p −
∂p
∂z
k =−∇p (9.55)
