Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

10.4 Frictionless baroclinic ﬂow 281

will be discussed in some detail in connection with the so-called quasi-geostrophic

theory (the second term on the right-hand side).

(iii) The solenoidal effect, i.e. the number of solenoids per unit area (the last term on the

right-hand side).

It is of some advantage to express the vorticity equation in the p system, in

which pressure is the vertical coordinate. In this system the solenoidal term does

not appear explicitly. Again, the starting point is Ertel’s vortex theorem (10.61), to

which we apply the following simpliﬁcations.

(i) We omit the vertical component w of the relative velocity from the term ∇×v

(ii) We omit the horizontal component l in 2Ω.

(iii) We apply the metric simpliﬁcation u/r = v/r = 0 as in (10.69).

(iv) We apply the hydrostatic approximation.

These simpliﬁcations are summarized next, together with the resulting approx-

imation of the curl of the absolute velocity in the geographical coordinate system

(λ, ϕ, r). The deformation velocity is approximated as a one-component vector. It

is also assumed that W

depends only on p so that the curl of v

vanishes:

= v + v

+ v

= v

+ Ω × r + q

∇×v

= 2Ω = f e

, ∇×v

= 0,

= 0

∇×v

=∇×v

+ f e

=−e

∂v

∂r

+ e

∂u

∂r

+ e

(ζ + f )

= e

∂v

∂r

+ e

η =−gρ e

∂v

∂p

+ e

where ζ =

cos ϕ



∂

∂λ

(rv) −

∂

∂ϕ

(rucos ϕ)



(10.72)

The hydrostatic approximation was introduced as the last step. Next the general

ﬁeld function ψ will be replaced in (10.61) by the pressure coordinate p.By

splitting the gradient of p into its horizontal (∇

p) and vertical (e

∂p/∂r )parts,

observing (10.72) and the hydrostatic relation, we easily ﬁnd from vector-analytic

operations the expression

α ∇p ·∇×v

=−g ∇

p · e

∂v

∂p

− gη (10.73)

Therefore, Ertel’s theorem can be written as



η +∇

p · e

∂v

∂p



=∇

˙p · e

∂v

∂p

+ η

∂ ˙p

∂p

(10.74)

282 Circulation and vorticity theorems

To complete the transformation to the (λ, ϕ, p) system we replace the horizontal

gradient by the horizontal gradient in the p system:

∇

=∇

h,p

+ ρ(∇

h,p

φ)

∂

∂p

(10.75)

The proof of this equation is left as an exercise. Now we use (10.75) to establish

a relation between the absolute vorticities in these two systems. On applying the

operators in the form e

·∇×v

, we ﬁnd by splitting v and ∇ into their horizontal

and vertical parts, for ζ

ζ = e

·∇×v = e

·∇

× v

= e

·∇

h,p

× v

+ ρe

·∇

h,p

φ ×

∂v

∂p

= ζ

− ρ ∇

h,p

φ ·



∂v

∂p



or η = η

− ρ ∇

h,p

φ ·



∂v

∂p



with ζ

= e

·∇

h,p

× v

(10.76)

On replacing ∇

(···) in (10.74) by (10.75) and recognizing that the horizontal

pressure gradient in the p system vanishes, we ﬁnd

dη



∂v

∂p



·∇

h,p

ω + η

∂ω

∂p

(10.77)

The change in pressure dp/dt = ˙p has been replaced by the vertical velocity ω

in the p system and in the absolute vorticity η

. This very useful equation and

its application will be discussed in some detail in conjunction with the quasi-

geostrophic theory. Once again it is pointed out that the solenoidal term does

not appear explicitly since we have replaced ψ by p in (10.61). Since a coordinate

transformation cannot change the physical content of the vorticity equation (10.70),

the solenoidal effect must then be hidden in the remaining terms.

10.4.5 Rossby’s formulation of the potential vorticity

Originally Rossby (1940) used the metrically simpliﬁed horizontal equations of

motionintheθ system to obtain a very useful conservative quantity known as the

Rossby potential vorticity. To demonstrate once again the central role of Ertel’s

vortex theorem we will not follow the original derivation but proceed differently.

Since Rossby assumed frictionless isentropic dry air motion (

θ = 0), we put ψ = θ

10.4 Frictionless baroclinic ﬂow 283

in (10.61). As a ﬁrst step in the derivation we combine the equation of potential

temperature with the ideal-gas law and ﬁnd

∇θ

∇α

∇p

(10.78)

where c

and c

are the speciﬁc heats at constant pressure and volume, respectively.

In view of (10.78) we recognize that the entire right-hand side of (10.61) vanishes.

The resulting conservation law

(α ∇×v

·∇θ) = 0

(10.79)

will now be rewritten in the form proposed by Rossby. As before, we decompose

the gradient operator of the scalar function into its horizontal and vertical parts.

The conserved quantity, using (10.72), assumes the form

(α ∇×v

·∇θ) = α



∂v

∂r

+ e





∇

θ + e

∂θ

∂r



=−g



∇

θ · e

∂v

∂p

+ η

∂θ

∂p



(10.80)

where, once again, we have used the hydrostatic approximation.

Next, we wish to introduce pressure as the vertical coordinate. Using the trans-

formation rules of partial derivatives as discussed in Section M4.2, we readily

ﬁnd

∇

h,q

3 =∇

h,ξ

− (∇

h,ξ

)

∂

∂q

(10.81)

When we apply this equation to the potential temperature we obtain the relation

of the horizontal gradients in the two systems using r = q

and p = ξ as vertical

coordinates:

∇

h,r

θ =∇

h,p

θ + ρ

∂θ

∂p

∇

h,p

φ (10.82)

Now we replace the horizontal gradients in (10.79) by means of (10.82), using

(10.76), and ﬁnd



∇

h,p

θ ·



∂v

∂p



+ η

∂θ

∂p



= 0(10.83)

Here the conserved quantity P

=∇

h,p

θ ·



∂v

∂p



+ η

∂θ

∂p

(10.84)

is Rossby’s formulation of the potential vorticity in the p system.

284 Circulation and vorticity theorems

Before we discuss this very useful concept in some detail, we wish to transform

(10.83) so that the potential temperature rather than the pressure appears as the

vertical coordinate. We accomplish this by ﬁrst setting q

= θ and ξ = p in

(10.81). With the help of the hydrostatic equation we ﬁnd

∇

h,θ

=∇

h,p

−

∂p

∂θ

∇

h,p

∂

∂p

(10.85)

In order to introduce the vorticity with respect to an isentropic surface, we take the

vector product of the operators appearing in (10.85) with the horizontal velocity

and then use scalar multiplication by the vertical unit vector of the geographical

coordinates. The result is

·∇

h,θ

× v

= ζ

= e

·∇

h,p

× v

−

∂p

∂θ

·∇

h,p

θ ×

∂v

∂p

(10.86)

= ζ

−

∂p

∂θ

·∇

h,p

θ ×

∂v

∂p

= η

−

∂p

∂θ

·∇

h,p

θ ×

∂v

∂p

(10.87)

The equation for the absolute vorticity has been found by adding f to both sides of

the ﬁrst equation. Equation (10.87) relates the two systems with potential temper-

ature and pressure as vertical coordinates. As the ﬁnal step we eliminate η

from

(10.83) with the help of (10.87) and ﬁnd the desired expression



∂θ

∂p



= 0

(10.88)

If the assumptions leading to this equation are satisﬁed then the potential vorticity

is invariant or a conservative quantity along the trajectory of an air parcel. The term

∂θ/∂p is a measure of hydrostatc stability.

Before applying this conservation rule to a problem of large-scale motion we

will obtain from (10.88) an approximate but useful formula. From thermodynamics

and atmospheric statics the following expression can be easily derived:

∂θ

∂p

=−

− γ

gρ

(10.89)

where γ

= g/c

p,0

and γ

represent the dry adiabatic and the observed lapse rates.

Next, we approximate the actual wind shear by the thermal wind in the (x, y,p)-

coordinates, see (9.69),

∂v

∂p

≈−

×∇

h,p

T (10.90)

10.4 Frictionless baroclinic ﬂow 285

Logarithmic differentiation of the deﬁning relation for the potential temperature

on isobaric surfaces yields

∇

h,p

θ =

∇

h,p

T (10.91)

With these relations (10.84) can be written as

=−(ζ

+ f )

− γ

(∇

h,p

T )

(10.92)

In a last step, expressing the velocity gradients in the Cartesian system on a

constant-pressure surface, we ﬁnally get





p,0



−





∂v

∂x



−



∂u

∂y



+ f



(γ

− γ





∂T

∂x





∂T

∂y





(10.93)

All quantities apprearing in this approximate relation can now be obtained from a

single map, provided that γ

is known.

Equation (10.88) is a powerful constraint on the large-scale motion of the atmo-

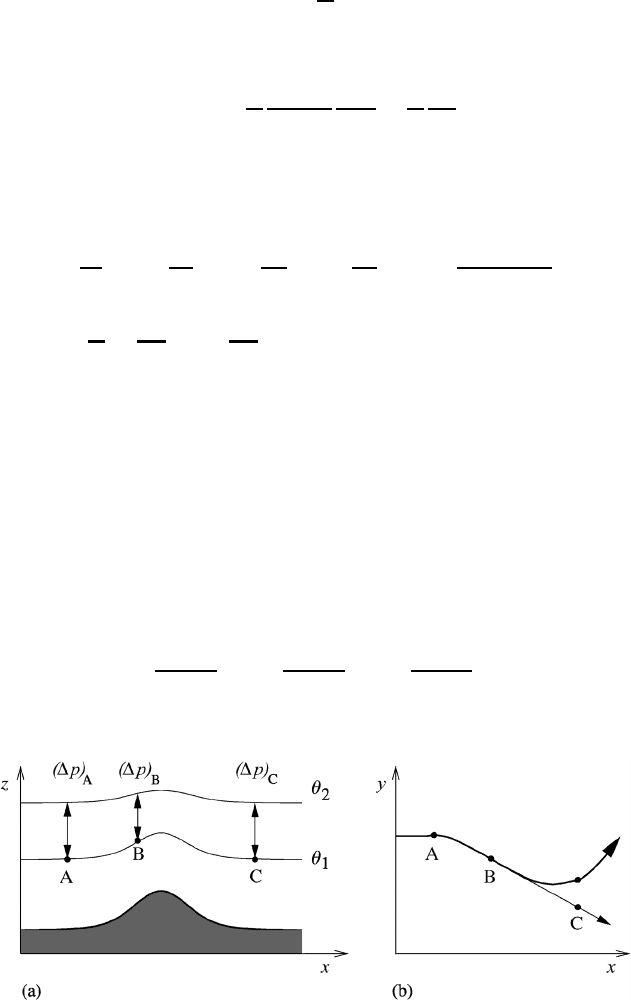
sphere, as will be illustrated by considering air ﬂow over a symmetric mountain

barrier oriented south–north; see Figure 10.2. Since the ﬂow is assumed to be isen-

tropic some distance above the ground where frictional effects are small, the air is

constrained to move between two isentropic surfaces that more or less follow the

contour of the ground. On writing (10.88) in ﬁnite differences for a ﬁxed value of

2θ,weﬁnd



+ f





+ f





+ f



(10.94)

Fig. 10.2 Westerly ﬂow over a south–north mountain barrier.

286 Circulation and vorticity theorems

since the potential vorticity is conserved. From this relation we my explain qual-

itatively the behavior of the trajectory of an air parcel as it crosses the mountain

barrier. Suppose that at position A there is straight-line ﬂow in the eastward di-

rection without any shear of the horizontal wind vector. We write the potential

vorticity in Cartesian coordinates



∂v

∂x



−



∂u

∂y



(10.95)

where the partial derivatives are evaluated along the θ-surface. Thus we immedi-

ately recognize that ζ

(A) = 0. When the air parcel begins to cross the mountain

range, the difference in pressure between the isentropic surfaces decreases so that

the relative vorticity over the mountain range must be negative in order to conserve

absolute vorticity; see part (b) of Figure 10.2. This results in anticyclonic curva-

ture of the trajectory in the northern hemisphere. After the air parcel has crossed

the mountain the difference in pressure between the two isentropic surfaces has

returned to its original value. Without the effect of the changing Coriolis parameter

the air parcel would have reached the position C, where straight line ﬂow would

result due to the assumed symmetry of the mountain barrier. This means that the

straight westerly ﬂow has changed to a ﬂow from the north-west. So far we have

assumed that the Coriolis parameter f remains constant. However, as the air parcel

is moving south, the Coriolis parameter is decreasing, thus causing the relative

vorticity to become positive so that the resulting trajectory would have a positive

curvature at C due to the conservation principle. The formation of the lee-side

trough is observed quite regularly to the east of the Rocky Mountains; see Bolin

(1950). Further details are given, for example, by Holton (1972) and Pichler (1997).

10.4.6 Helmholtz’s baroclinic vortex theorem

The general vortex theorem in the absolute system (10.54) can be used to deduce

Helmholtz’s famous vortex theorem, which is the starting point for the derivation

of some circulation laws to be discussed in detail. On replacing ψ by (x, y,z)

successively in (10.54) with (∇x = i, ∇y = j, ∇z = k)and(˙x = u

, ˙y = v

, ˙z =

) we obtain

(α ∇×B

· i) −α ∇×B

·∇u

= 0

(α ∇×B

· j) −α ∇×B

·∇v

= 0

(α ∇×B

· k) −α ∇×B

·∇w

= 0

(10.96)

10.4 Frictionless baroclinic ﬂow 287

On performing dyadic multiplication of these equations by the unit vectors i, j, k

and adding the resulting equations the vector α ∇×B

is obtained since scalar

multiplication of a vector by the unit dyadic gives the vector itself. Hence we obtain

(α ∇×B

) − α ∇×B

·∇v

= 0(10.97)

Carrying out the differentiation and using the continuity equation immediately

leads to the baroclinic version of the Helmholtz vortex theorem:

(∇×B

) =∇×B

·∇v

−∇·v

(∇×B

)

(10.98)

This theorem states, for example, that ∇×B

remains zero at all times if it is

zero at time t = 0. This statement is not immediately obvious but requires a brief

mathematical discussion.

First of all we expand ∇×B

in a Taylor series about the time t = 0:

∇×B

= (∇×B

)

t=0

+ t



(∇×B

)



t=0



(∇×B

)



t=0

+···

(10.99)

If ∇×B

= 0att = 0 then (10.98) shows that



(∇×B

)



t=0

= 0(10.100)

On differentiating (10.98) with respect to time we ﬁnd without difﬁculty, using

(10.100), that



(∇×B

)



t=0

= 0(10.101)

Continuing this procedure veriﬁes the assertion that, if ∇×B

= 0att = 0, it

remains zero at all times, as now follows from (10.99).

Finally, we wish to state the Helmholtz theorem in a more practical form for the

rotating earth. This is accomplished by substituting (10.43b) into (10.98) in order

to replace the Weber transformation. The result is



∇×(v + v

) −∇β ×∇s





∇×(v + v

) −∇β ×∇s



·∇(v + v

)

−



∇×(v + v

) −∇β ×∇s



∇·(v + v

)

(10.102)

For the relative system with rigid rotation we may use the following identities:

= Ω × r, ∇×v

= 2Ω, ∇v

=−E × Ω, ∇·v

= 0

(∇×B

) =

(∇×B

)



=q

(t)

+∇×B

·∇v

∇×B

·∇v

=−(∇×B

) × Ω

(10.103)

288 Circulation and vorticity theorems

By substituting (10.103) into (10.102) we ﬁnally ﬁnd

(∇×v + 2Ω −∇β ×∇s)



=q

(t)

= (∇×v + 2Ω −∇β ×∇s) · (∇v −∇·vE)

(10.104)

In this form Helmholtz’s theorem is not so easily interpreted in meteorological

terms. However, this theorem is the starting point for the derivation of circulation

theorems that give much physical insight.

10.4.7 Thomson’s and Bjerkness’ baroclinic circulation theorems

Helmholtz’s baroclinic vortex law (10.98) can be transformed into an integral state-

ment by using a theorem for the motion of material surfaces S, see Section M6.5.2:





A · dS







+ A ∇·v

− A ·∇v



·dS =



·dS (10.105)

First we set A =∇×B

in (10.105). Next we integrate (10.98) over the surface

S. Comparison of these two equations gives





∇×B

· dS







(∇×B

) + (∇×B

)∇·v



· dS

−



(∇×B

) ·∇v

· dS = 0

(10.106)

Application of Stokes’ integral theorem results in the so-called baroclinic version

of Thomson’s circulation theorem in the absolute system,





∇×B

· dS







· dr



= 0 (10.107)

This is not a very explicit form. Therefore, we replace the Weber transformation

(10.43a) in this equation and ﬁnd





· dr







· dr



−







−





β ∇s · dr







· dr



−





β ∇s · dr



= 0

(10.108)

10.4 Frictionless baroclinic ﬂow 289

since the closed line integral of d

vanishes. Next we deﬁne the absolute and

the relative circulation:



· dr,C=



v · dr

(10.109)

Using the deﬁnition of the absolute circulation gives a second version of Thomson’s

circulation theorem:





β ∇s · dr







βd



(10.110)

On replacing the absolute velocity in (10.108), assuming rigid rotation of the

coordinate system, we obtain Bjerkness’ circulation theorem,





(v + v

− β ∇s) · dr



= 0or





(−v

+ β ∇s) · dr



(10.111)

This very useful version of the circulation theorem is easily interpreted and will be

discussed in detail in the next section.

10.4.8 Interpretation of Bjerkness’ circulation theorem

The interpretation of this theorem is facilitated by rewriting (10.111). With the help

of (10.65) we ﬁnd





· dr







∇×v

· dS



= 2Ω ·

(10.112)

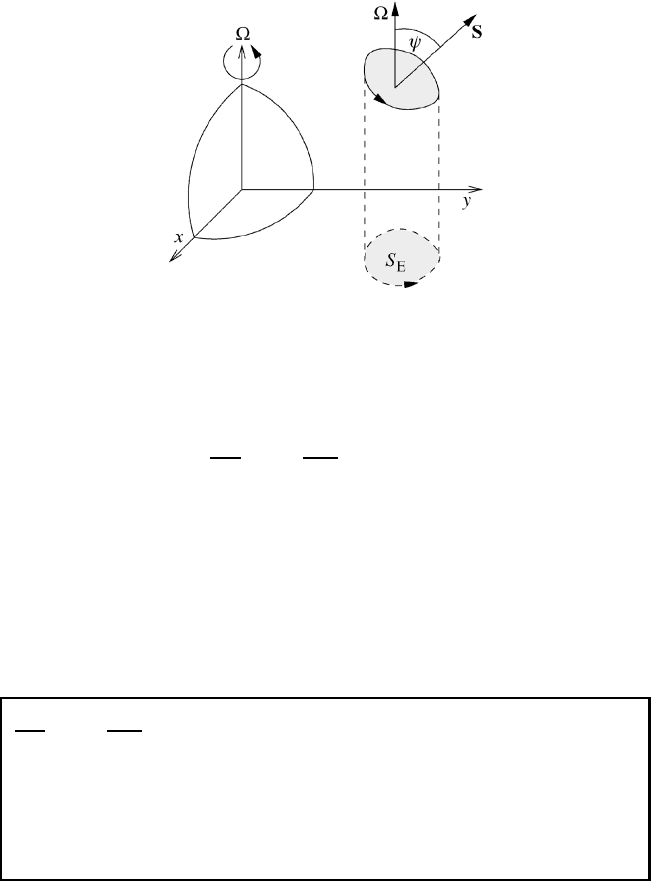
where use of the Stokes integration theorem has been made. We recognize from

Figure 10.3 that

= S ·

Ω

(10.113)

is the projection of the integration surface onto the equatorial plane. By using the

differentiation rule for the closed line integral we ﬁnd (see problem 10.5)





β ∇s · dr







dβ

s −



(10.114)

290 Circulation and vorticity theorems

Fig. 10.3 Projection of the surface of integratio

S onto the equatorial plane.

Since isentropic processes were assumed in all derivations leading to the circu-

lation laws, we have to set ds/dt = 0. Furthermore, recalling that dβ/dt = T ,we

ﬁnd from (10.111)

+ 2$



s (10.115)

By integrating equation (10.18) over the closed curve 6 we ﬁnd



s =



h −



αd

p =−



(αp) +



α =



α (10.116)

since closed line integrals of the exact differentials must vanish. With the help of

Stokes’ integral theorem we ﬁnally ﬁnd the following three versions of Bjerkness’

circulation theorem:

+ 2$



s =



T ∇s · dr =



∇T ×∇s · dS

=−



αd

p =−



α ∇p · dr =−



∇α ×∇p · dS



α =



p ∇α · dr =



∇p ×∇α · dS

(10.117)

Whenever the acceleration of the circulation dC/dt > 0 we speak of the direct

circulation;whendC/dt < 0 it is called the indirect circulation. The vector

∇α ×∇p describing the baroclinicity of the system is called the baroclinicity

vector N. As can be seen from Figure 10.4, two sets of intersecting surfaces

α = constant and p = constant divide a particular volume into a continuous

family of isosteric–isobaric tubes. These tubes are called solenoids. In the vertical

cross-section depicted in Figure 10.4 they appear as parallelogram-type ﬁgures.