Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

11.5 Budget equations of the turbulent system 311
be called the turbulent system. This is done by averaging the molecular form
(M6.66) of the budget equation. By steps that are now well known we find
∂
∂t
(ρ
ψ) +∇·(
v
A
ρ
ψ) +∇·(v
ρψ
) +∇·F
ψ
= Q
ψ
(11.32)
since v
A
ρψ =
v
A
ρ
ψ + v
ρψ
. Instead of one term describing the molecu-
lar convective flux or molecular transport term, we have two terms, i.e.
v
A
ρ
ψ
representing the mean convective flux in the turbulent system plus the turbulent
flux F
ψ,t
= v
ρψ
. Using the operator (11.23) we obtain the budget equation of the
turbulent system in the form
D
Dt
(ρ
ψ) +∇·(F
ψ
+ F
ψ,t
) = Q
ψ
(11.33)
Next we are going to apply this equation to various state variables. For reasons
of clarity we first collect the prognostic equations of the molecular system. These
are the continuity equation for the total mass (M6.67), the continuity for the partial
masses or concentrations (M6.72), the first law of thermodynamics (M6.73), and
the equation of motion (1.71):
Dρ
Dt
= 0
D
Dt
(ρm
k
) =−∇·J
k
+ I
k
D
Dt
(ρe) =−∇·(J
h
+ F
R
) − p ∇·v
A
+ !
D
Dt
(ρv) =−∇p − ρ ∇φ − 2ρΩ × v +∇·
J
(11.34)
where ! =
J ··∇v
A
is the dissipation of energy. These equations will then be
averaged using the averaging procedures we have discussed so thoroughly above.
The results are
(a)
Dρ
Dt
=0
(b)
D
Dt
ρ m
k
=−∇·J
k
−∇·J
k
t
+ I
k
(c)
D
Dt
(
ρ e ) =−∇·J
h
−∇·F
R
−∇·J
h
t
− p ∇·
v
A
+ v
·∇p + !
(d)
D
Dt
(
ρ
v ) =−∇p +∇·J −∇·J
t
− ρ ∇φ + 2ρ ×
v
(11.35)

312 Turbulent systems
One essential part, in contrast to the molecular system, is the appearance of the
turbulent flux terms F
ψ,t
. These are given by
J
k
t
= v
ρm
k
, J
h
t
= v
ρh, J
t
= v
ρv
A
(11.36)
where h = e + pα is the enthalpy. The reason why the term J
e
t
= v
ρe does
not appear is left as a problem. For the turbulent diffusion flux J
k
t
and the mean
molecular phase transitions
I
k
the following summation conditions hold:
3
k=0
J
k
t
= v
ρ
3
k=0
m
k
= ρv
= ρ
v
= 0
I
0
= 0,
3
k=1
I
k
= 0
(11.37)
The turbulent momentum flux tensor
J
t
and the Reynolds tensor R, which is fre-
quently used in the literature, are related by
R =−v
ρv
A
=−v
ρv
=−J
t
(11.38)
A few remarks about the meaning of the turbulent fluxes may be helpful. Consider
a test volume V moving approximately with the average velocity
v
A
so that during
time step t the volume is displaced the distance
v
A
t. Fluid elements, however,
are moving with the velocity
v
A
+v
. During this time step the velocity fluctuations
cause some fluid to enter the test volume at some parts of the imagined volume
boundary while at other sections of the boundary some fluid leaves the test volume.
While the total mass is conserved on average, as is guaranteed by the continuity
equation, there is no reason to believe that the quantity #
V
=
V
ρψ dV
is
conserved also. In fact #
V
may be viewed as the total content of the property ψ
within the volume V at a particular time. Since #
V
changes with time, there must
exist a flux that is penetrating the volume surface of the fluid volume. It now stands
to reason that F
ψ,t
= v
ρψ, as listed in (11.36), may be interpreted as the turbulent
flux which is the mean ψ stream through the surface of V which is moving with
the velocity
v
A
. In a later chapter it will be shown that, within the framework of
this discussion, the turbulent flux is directed from regions of higher to lower ψ
values so that this flux causes an equalization of the ψ field. Occasionally, there are
situations in which the transport appears to flow against the gradient. This is known
as the counter-gradient flow, which is really not well understood at this time and
will be left out of our discussion.
We close this section with a remark on the Hesselberg average. Only specific val-
ues of extensive variables (
v,e,
h,α) and their derivatives with respect to intensive
coordinates p and T carry the roof symbol
.
11.6 The energy budget of the turbulent system 313
11.6 The energy budget of the turbulent system
Our next step is to show that the total energy budget of the turbulent system is
balanced or source-free. In order to proceed efficiently, we again take the energy
budget of the molecular system in the absence of deformational effects (v
D
= 0).
The system consists of the budget equation for the potential energy as expressed
by the geopotential, the budget equation for the kinetic energy, and the first law of
thermodynamics:
(a)
D
Dt
(ρφ) = ρv ·∇φ
(b)
D
Dt
ρv
2
2
+∇·
v · (p
E − J)
=−ρv ·∇φ + p ∇·v − !
(c)
D
Dt
(ρe) +∇·(J
h
+ F
R
) =−p ∇·v + !
(11.39)
For later convenience we add the enthalpy equation
D
Dt
(ρh) +∇·(J
h
+ F
R
) =
dp
dt
+ ! (11.40)
This equation may be easily obtained by substituting into (11.39c) e = h −pα and
∇·v = ρdα/dt with α = 1/ρ. We recall that quantities depending explicitly on
r and t are not averaged in the microphysical sense. This includes the geopotential
φ = gz.
First of all we direct our attention to averaging (11.39b) by using (11.23). The
result is
D
Dt
ρ
v
2
2
+∇·
v · (pE − J) + v
ρv
2
2
=−ρ
v ·∇φ +p ∇·v − ! (11.41)
By using the expressions
v
ρv
2
2
= k
t
−
v · R, k
t
= v
ρv
2
2
p ∇·v = p ∇·
v +∇·(v
p) − v
·∇p
v · (pE − J) =
v · (pE − J) + v
p − v
· J
(11.42)
we obtain for (11.41) the budget equation for the total kinetic energy:
D
Dt
ρ
v
2
2
+∇·
v · (
pE − J − R) − v
· J + k
t
=−
ρ
v ·∇φ + p ∇·
v − v
·∇p − !
(11.43)
314 Turbulent systems
The vector k
t
describes the turbulent flux of turbulent kinetic energy. Note that the
effect of the earth’s rotation does not appear in the equation of the kinetic energy
(molecular or turbulent) since the Coriolis force does not perform any work.
Our next goal is to find an expression for the turbulent kinetic energy
k which is
defined by means of
k =
v
2
2
=
v
2
2
−
v
2
2
(11.44)
In order to proceed we must derive an expression for the kinetic energy
v
2
/2ofthe
mean motion. Scalar multiplication of the equation of mean motion (11.35d) by
v
yields
D
Dt
ρ
v
2
2
+∇·
v · (
pE − J − R)
=−ρ
v ·∇φ + p ∇·
v −∇
v··(J + R)
(11.45)
Now we subtract this expression from (11.43) and obtain the prognostic equation
for the turbulent kinetic energy:
D
Dt
(
ρ
k) +∇·(k
t
− v
· J) =∇
v··(J + R) − ! − v
·∇p
(11.46)
The turbulent budget system is completed by stating the prognostic equations for
the potential energy,
D
Dt
(
ρφ) = ρ
v ·∇φ
(11.47)
and the internal energy,
D
Dt
(
ρ e ) +∇·(J
h
+ F
R
+ J
h
t
) =−p ∇·
v + v
·∇p + !
(11.48)
The fact that we have introduced J
h
t
instead of J
e
t
is responsible for the appearance
of the term v
·∇p. By adding equations (11.45)–(11.48) we find that the sum
of all source terms vanishes. Thus, we conclude that the energy budget of the
turbulent system is balanced. The reader may wish to display graphically the
energy transformations by repeating the procedure used for the molecular system.
Of special interest in the energy transformations is the interaction of the turbulent
kinetic energy and the internal energy by means of the advection-type term
v
·∇p.
If this term is positive a loss of turbulent kinetic energy occurs in favor of the internal
energy. A loss of turbulent kinetic energy represents a damping effect that occurs
11.7 Diagnostic and prognostic equations of turbulent systems 315
for stable atmospheric stratification. If this source term is negative, turbulence will
increase, which is indicative of unstable atmospheric stratification. It should be
noted that the representation (11.45)–(11.48) is not unique. By some mathematical
manipulations it is possible to separate the source terms in a different way but the
sum of the sources still adds up to zero.
For later convenience we will also average the enthalpy equation (11.40) of the
molecular system, resulting in
D
Dt
(
ρ
h) +∇·(J
h
+ J
h
t
+ F
R
) =
d
p
dt
+
v
·∇p + ! (11.49)
11.7 Diagnostic and prognostic equations of turbulent systems
We begin with a simple example by considering the ideal-gas law of the molecular
system as given by
p = R
0
ρT
v
(11.50)
where T
v
is the virtual temperature and R
0
the gas constant of dry air. Taking the
Reynolds average to simulate a turbulent system, we find
p
R
0
= ρT
v
+ ρ
T
v
(11.51)
The final term of this equation containing the fluctuations is usually much smaller
in magnitude than the remaining terms. Ignoring the fluctuation term, the ideal-gas
law in the mean retains the molecular form (11.50),
p = R
0
ρT
v
(11.52)
Another approach is to postulate a general diagnostic formula in order to avoid
the appearance of correlations to begin with. Proceeding in this manner, a par-
ticular diagnostic equation of the turbulent system is identical in form with the
corresponding molecular equation. To set the pattern, we make use of the general
diagnostic equation which is discussed more thoroughly in TH:
(a) ψ = ψ
n
m
n
,ψ
k
= ψ
k
(p,T,m
0
,m
1
,m
2
,m
3
)
(b) dψ =
∂ψ
∂p
T,m
k
dp +
∂ψ
∂T
p,m
k
dT + ψ
n
dm
n
(11.53)
Here we make use of the Einstein summation convention which omits the summa-
tion sign in the expression ψ
n
m
n
.Thetermψ represents various thermodynamic
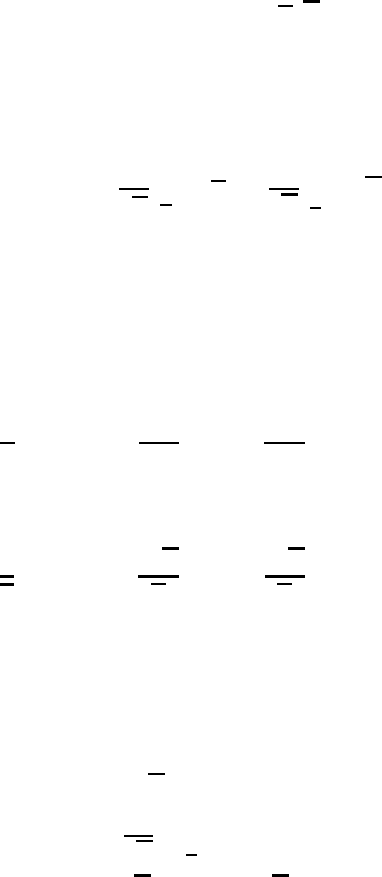
316 Turbulent systems
functions, such as internal energy, enthalpy, entropy, specific volume, and others.
ψ
k
is known as the specific partial quantity of #. Next we define the function
ψ =
ψ
n
m
n
,
ψ
k
= ψ
k
(p, T,m
0
, m
1
, m
2
, m
3
)(11.54)
which applies to the turbulent system. The tilde above ψ
k
does not represent an
average value itself but rather represents a function depending on the average state
variables. Analogously to (11.53) we obtain for the turbulent system
d
ψ =
∂
ψ
∂p
T,m
k
d
p +
∂
ψ
∂T
p,m
k
d
T +
ψ
n
dm
n
(11.55)
The operator
d is defined in (11.21). A few examples will clarify the meaning of
(11.55).
Example 1 In the first example we give the equation of state consisting of dry air,
water vapor, liquid water, and ice
α =
1
ρ
= α
n
m
n
=
R
0
T
p
m
0
+
R
1
T
p
m
1
+ α
2
m
2
+ α
3
m
3
(11.56)
The corresponding statement for the turbulent system is
α =
1
ρ
= α
n
m
n
=
R
0
T
p
m
0
+
R
1
T
p
m
1
+ α
2
m
2
+ α
3
m
3
(11.57)
since α
2
,α
3
= constant.
Example 2 The differential of the enthalpy of the turbulent system is obtained by
setting ψ = h in (11.55) so that
d
h =c
p
d
T +
h
n
dm
n
with c
p
=
∂
h
∂T
m
k
,p
= c
p,n
m
n
,c
p,k
= constant
h
k
=
h
k
(T = T
0
) + c
p,k
(T − T
0
)
(11.58)
Here we have assumed that the pressure dependency of the enthalpy can be ignored.
This assumption is rigorously true for any ideal gas.
Equation (11.58) can be used to obtain the prognostic equation for the temper-
ature of the turbulent system. First we multiply (11.58) by the density and then
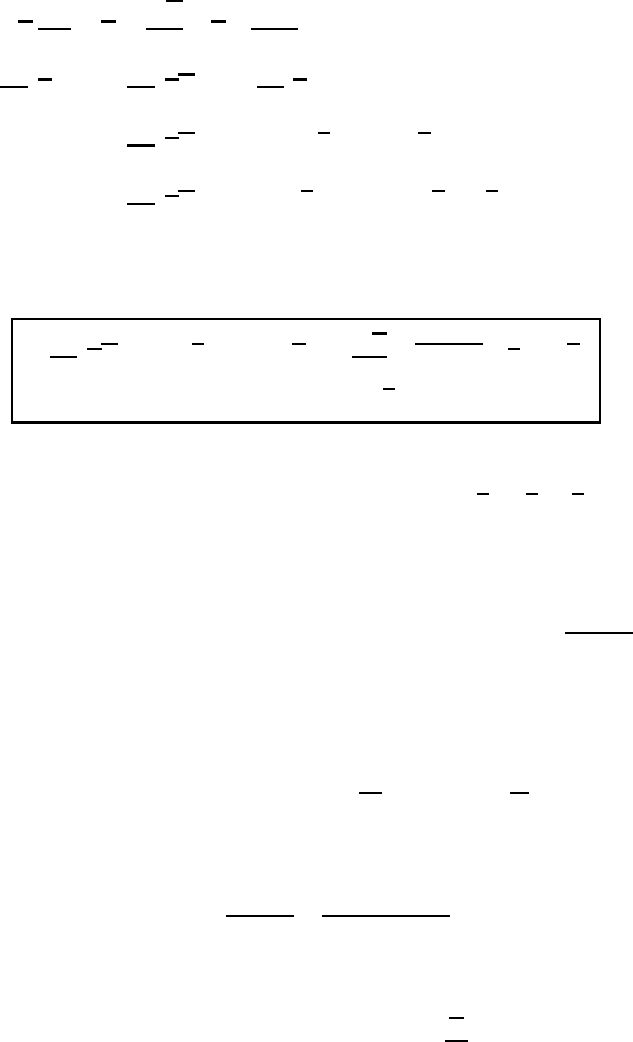
11.7 Diagnostic and prognostic equations of turbulent systems 317
divide the result by dt.Nextweeliminate
dm
k
/dt with the help of (11.35b), to find
ρ
d
h
dt
=
ρ c
p
d
T
dt
+
ρ
h
n
d m
n
dt
=⇒
D
Dt
ρ
h
=c
p
D
Dt
ρT
+
h
n
D
Dt
(
ρm
n
)
=c
p
D
Dt
ρT
+
h
n
−∇ · (
J
n
+ J
n
t
) + I
n
=c
p
D
Dt
ρT
−∇·
h
n
(J
n
+ J
n
t
)
+
h
n
I
n
+ (J
n
+ J
n
t
) ·∇
h
n
(11.59)
By substituting this equation into (11.49) we obtain the prognostic equation for the
temperature:
c
p
D
Dt
ρT
+∇·(J
h
s
+ J
h
s,t
+ F
R
) =
d p
dt
+
v
·∇p + ! −
h
n
I
n
− (J
n
+ J
n
t
) ·∇
h
n
(11.60)
In this equation the following fluxes appear:
the mean molecular sensible enthalpy flux:
J
h
s
= J
h
− J
n
h
n
the turbulent sensible enthalpy flux: J
h
s,t
= J
h
t
− J
n
t
h
n
the turbulent latent enthalpy flux: J
h
l,t
= J
n
t
h
n
(11.61)
In several equations, e.g. (11.35), (11.43), and (11.60), the term
v
·∇p,which
is very awkward to handle, appears. Since there is no reason to ignore this term, we
will try to replace it by a reasonable approximation. To simplify the mathematical
treatment we begin with the molecular system of dry air which is described by
p = R
0
ρT, ( =
p
p
0
k
0
,θ=
T
(
(11.62)
where ( is the Exner function, k
0
= R
0
/c
p,0
,andθ is the potential temperature.
With the help of these expressions we easily obtain
v
·∇p = ρc
p,0
θv
·∇( (11.63)
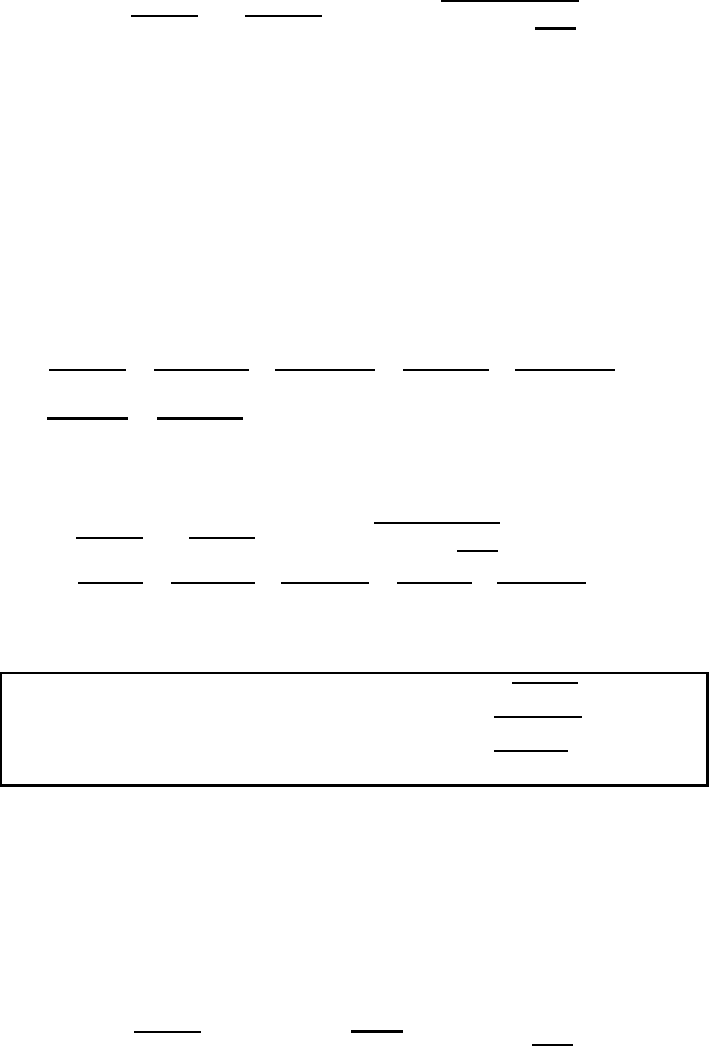
We decompose the Exner function as shown in
( =
( + (
with
( =
p
p
0
k
0
(11.64)
318 Turbulent systems
Substituting (11.64) into (11.63) gives
v
·∇p =
(ρc
p,0
θv
·∇ln
( +
(ρc
p,0
θv
·
∇(
(
(11.65)
Before proceeding we wish to remark that, with the help of the entropy-production
equation and the so-called linear Onsager theory, it is possible to obtain proper
parameterized expressions for various fluxes. This subject is thoroughly discussed
in various textbooks on thermodynamics. Often one speaks of the phenomenolog-
ical theory. We refer to TH.
The first term on the right-hand side of (11.65) has the desired form required by
the linear Onsager theory which will be used later to find proper expressions for
various turbulent fluxes. The first factor in each of the expressions on the right-hand
side is a flux while the second factor is the thermodynamic force. For reasons that
will become apparent later we split the flux:
(
ρc
p,0
θv
= ρc
p,0
θ(v
− ρc
p,0
θ(
v
= ρc
p,0
T
v
− ρc
p,0
θ(
v
(11.66)
since
ρc
p,0
T v
= ρc
p,0
T
v
. In a simplified manner we now extrapolate from the
system of dry air to the general multicomponent system by replacing c
p,0
in (11.66)
by c
p
= c
p,n
m
n
. We proceed analogously with (11.65). The result is
v
·∇p =
(ρc
p
θv
·∇ln
( +
(ρc
p
θv
·
∇(
(
(ρc
p
θv
= ρc
p
θ(v
− ρc
p
θ(
v
= ρc
p
T
v
− ρc
p
θ(
v
(11.67)
The heat fluxes appearing in the above equations are given the following names:
the turbulent heat flux: J
θ
t
=
(ρc
p
θv
the turbulent Exner flux: J
(
t
= ρc
p
θ(
v
the turbulent sensible enthalpy flux: J
h
s,t
= ρc
p
T
v
(11.68)
They are related by
J
θ
t
= J
h
s,t
− J
(
t
(11.69)
Note that neglecting the pressure fluctuation term (
results in an identity of
the heat flux J
θ
t
and the sensible enthalpy flux J
h
s,t
. Very often we do not distinguish
between these two fluxes since
J
(
t
is usually very small in comparison with
J
θ
t
.
Utilizing the expressions derived above, equation (11.65) can finally be written
as
v
·∇p = J
θ
t
·∇ln
( + J
θ
t
· A with A =
∇(
(
(11.70)
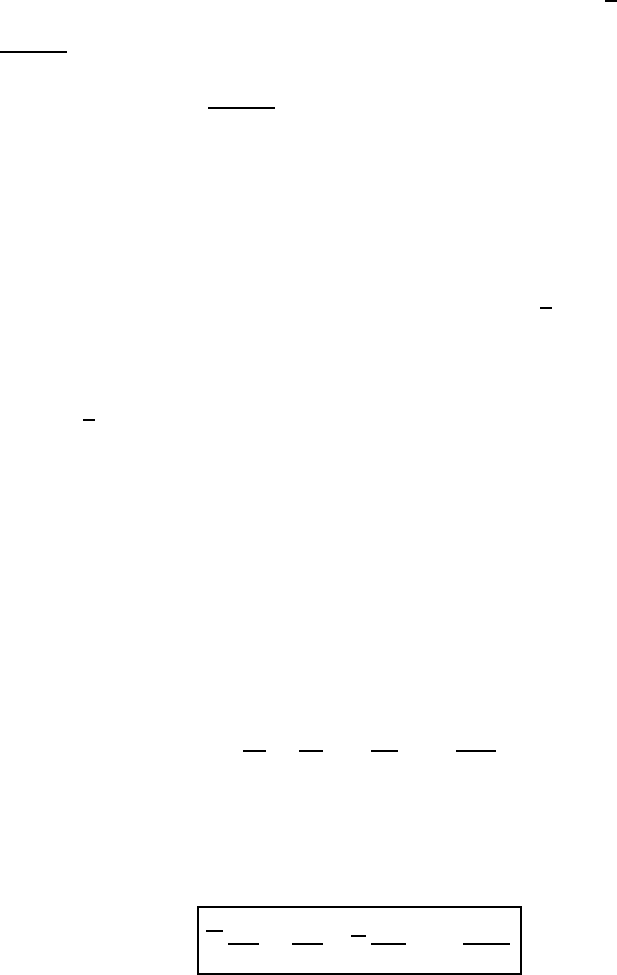
11.8 Production of entropy in the microturbulent system 319
It should be noted that the second term on the right-hand side of (11.70) cannot be
evaluated in terms of the phenomenological equations by using the theory in the
form presented here. The same is also true for the energy dissipation
!.
In this section we have obtained an approximate parameterization of the term
v
·∇p, but we have failed to derive an expression for the dissipation of energy. A
different approach in the treatment of the thermodynamics of turbulent systems is to
avoid the appearance of
v
·∇p altogether. This can be done by identifying some of
the variables of the turbulent system with average values of the molecular system.
The remaining variables must be defined in a suitable manner. One possible way to
proceed is described by the so-called exclusive system. The curious name derives
from the treatment of the internal energy of the system which excludes, or, which
amounts to the same thing, does not include, the turbulent kinetic energy. While
this system offers various advantages, it does not provide a method by which one
can find the Reynolds tensor
R and the dissipation of energy ! without additional
assumptions. The least desirable property of the exclusive system is that energy is
not strictly conserved. In the more refined inclusive system the turbulent kinetic
energy is included as part of the internal energy. In this system it is still not possible
to obtain
! but the system does provide access to R. The theory is difficult and not
yet complete. For more details see the papers by Sievers (1982, 1984).
11.8 Production of entropy in the microturbulent system
In order to derive the proper forms of the various turbulent fluxes we employ the
entropy-production equation. This equation will now be derived for the microturbu-
lent system. The starting point in the derivation is Gibbs’ fundamental equation for
the molecular system. Again we refer to TH. If s is the entropy and µ
k
= h
k
−Ts
k
the chemical potential, then we have
T
ds
dt
=
de
dt
+ p
dα
dt
− µ
n
dm
n
dt
(11.71)
We assume that the Gibbs equation is also valid for the microturbulent system.
We proceed by introducing the proper variables and differential operators of the
microturbulent system in the form
T
d s
dt
=
d e
dt
+
p
d α
dt
−µ
n
d m
n
dt
(11.72)
We want to point out that this equation does not arise simply from averaging
(11.71), but rather must be introduced in the sense of an axiomatic statement. The
320 Turbulent systems
quantitities s and µ
k
are functions of the averaged state variables (p,T,m
k
). First
we introduce into (11.72) the continuity equation
d α
dt
= α ∇·
v
A
(11.73)
which follows from (11.35a). On multiplying (11.72) by the air density we find
T
D
Dt
(
ρ s) =
D
Dt
(
ρ e) + p ∇·
v
A
−µ
n
D
Dt
(
ρm
n
)(11.74)
Inspection of this equation shows that there are three derivative expressions. Two
of these will be eliminated by substituting the budget equations for the partial
concentrations (11.35b) and for the internal energy (11.35c) into (11.74), yielding,
after some slight rearrangement
s,
T
D
Dt
(
ρ s) =−∇·(J
h
+J
h
t
) +J
θ
t
·∇ln
( +!−µ
n
I
n
−∇·(J
n
+ J
n
t
)
(11.75)
We have omitted the radiative flux, which is obtained by solving the radiative-
transfer equation. Moreover, we have used (11.70) to replace
v
·∇p, assuming
that the second term on the right-hand side of this equation may be ignored. Now
we divide (11.75) by
T and write the resulting expression in budget form. We thus
obtain
D
Dt
(
ρ s) +∇·
1
T
J
h
+ J
h
t
−µ
n
(J
n
+ J
n
t
)
=
Q
s
(11.76)
with
Q
s
=−
µ
n
I
n
T
+
J
θ
t
T
·∇ln
( +
!
T
− (J
h
+ J
h
t
) ·
∇
T
T
2
− (J
n
+ J
n
t
) ·∇
µ
n
T
≥ 0
(11.77)
The inequality results from the fact that, according to the second law of thermody-
namics, the entropy production is positive definite.
To obtain convenient flux representations we are going to rewrite the entropy pro-
duction
Q
s
by using a well-known thermodynamic relation. For the microturbulent
system this identity may be written as
∇
µ
k
T
=
1
T
(∇µ
k
)
T
−
h
k
T
2
∇T (11.78)
For the molecular system the averaging symbols must be omitted. The subscript
T
indicates that the derivative is taken at constant
T . Substitution of this expression
