Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

The material and the local description of ﬂow

The kinematics of the atmosphere is the mathematical description of atmospheric

ﬂow ﬁelds without regarding the cause of the motion. Therefore, kinematics stands

in contrast to dynamics, in which the governing equations are derived from consid-

erations of forces acting on the ﬂuid particles. There exist two methods describing

the atmospheric motion. These are the methods of Lagrange and Euler. We shall

begin our discussion with the so-called material description of Lagrange, in which

the velocity ﬁeld is represented as a function of time at the position of the moving

particle.

3.1 The description of Lagrange

Suppose that x

are the initial coordinates of a ﬂuid particle at time t

and

the coordinates at some later time t.Ifx

,i= 1, 2, 3, can be expressed

as a function of the initial coordinates and the time, we know the history or the

trajectory of the particle. Formally, this can be stated as

= x





,i= 1, 2, 3(3.1)

so that, in the Lagrangian system, x

and t are the independent and x

the dependent

variables. Equation (3.1) is the formal parameter representation of the trajectory of

a particle whose initial position is x

. Changing the initial coordinates simply means

that we have selected a different ﬂuid particle. It is evident that (3.1) is the solution

of a system of prognostic equations for the trajectory of a particle as given by

= f

,t),i= 1, 2, 3(3.2)

A very simple example is dx

/dt = u = constant =⇒ x

,t) = x

+u(t −t

Lagrange’s method is characterized by the introduction of the so-called enumer-

ation coordinates a

,i= 1, 2, 3, which are simply the coordinates of the particle

at the initial time t = t

,i.e.a

= x

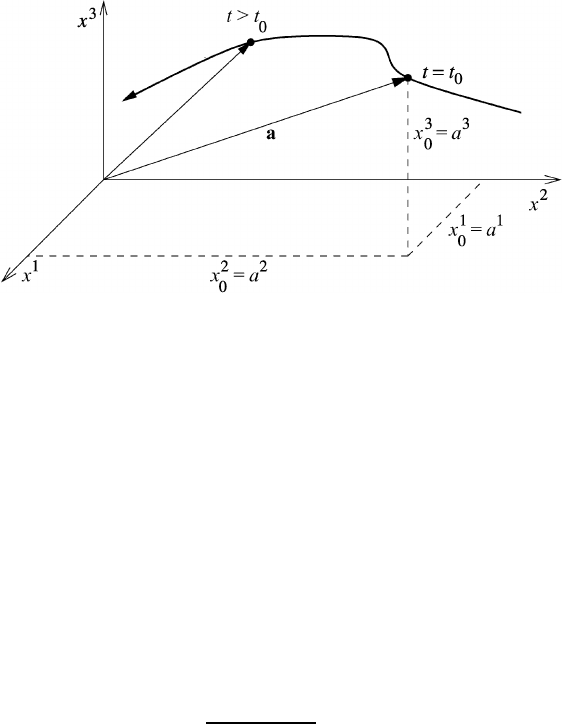
, as depicted in Figure 3.1.

171

172 The material and the local description of ﬂow

r(a, t)

Fig. 3.1 The position vector r of the trajectory of a particle. Initially the particle is at

position a.

For simplicity the selected initial coordinates are assumed to be Cartesian, but,

in general, any coordinate system could be used. The formal representation of the

trajectory may then be written as

= x

,t)orr = r(a,t)(3.3)

This representation also serves as the transformation equation between the coordi-

nates x

and a

= a

,t)ora = a(r,t)(3.4)

A unique transformation is possible only if the functional determinant of the

transformation differs from zero, i.e.



∂(x

)

∂(a

)



= 0(3.5)

In general, the a

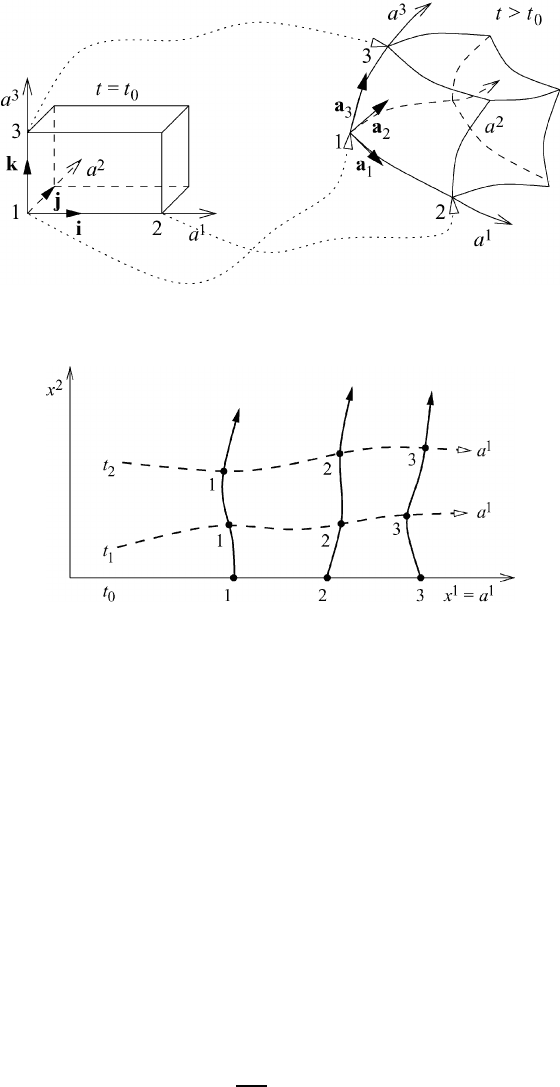
-coordinate system, as stated in (3.4), is curvilinear, nonortho-

gonal, and time-dependent, as displayed in Figure 3.2, where the initial coordinate

system is assumed to be the rectangular Cartesian system. For t>t

the original

orthogonal unit vectors will transform into nonorthogonal non-normalized basis

vectors.

It should be kept in mind that, in general, the displacement of individual particles

along their trajectories results in a deformation of the surfaces a

= constant.

Whereas in the original coordinate system the distance between any two particles,

for example two particles on the x

-axis with the distance δx

between them,

changes continually with time, the increment δa

between two arbitrary particles

remains unchanged since the enumeration coordinates of the particles are ﬁxed at

all times.

3.2 Lagrange’s version of the continuity equation 173

Fig. 3.2 Conceptional displacement of a material volume.

Fig. 3.3 Displacement of three particles aligned on the x

-axis at t = t

To clarify the idea, consider the following simpliﬁed two-dimensional coordinate

system of Figure 3.3, where three particles in their original positions are shown.

At time t = t

the coordinate axes x

and a

are identical and the distance between

the particles is δa

= 1. The distance δx

of the three particles moving along their

individual trajectories changes with time. Since the particles have ﬁxed enumeration

coordinates they remain neighboring particles on the a

-axis at all times so that the

-coordinate line must be drawn as shown.

3.2 Lagrange’s version of the continuity equation

3.2.1 Preliminaries

Consider an increment ds

along the coordinate line a

as given by

∂r

∂a

= a

(3.6)

174 The material and the local description of ﬂow

r(a, t

)

r(a, t

)

δσ

δr

Fig. 3.4 The tangential unit vector along the trajectory.

where the basis vector a

is shown in Figure 3.2. If the unit tangential vector

= a

√

to the coordinate line a

is introduced as well as the physical

coordinate a

= e

√

= e

(3.7)

then ds



becomes the arclength which is identical to an increment on the

physical coordinate line a

. The unit vector along the trajectory of a particular

particle is given by

t =



∂r

∂σ



(3.8)

where

δσ represents the arclength. On the trajectory the enumeration coordinates

,i= 1, 2, 3, are constant; see Figure 3.3.

For the velocity vector of the particle we may write

v =

dσ

(3.9)

The acceleration of an individual particle in the a

-coordinate system can be ob-

tained from the Eulerian development



∂v

∂t



+ ˙a

∂v

∂a

(3.10)

The important point is that the enumeration coordinates do not change with time,

so da

/dt = 0. Therefore, the acceleration in the Lagrangian system is given by



∂v

∂t



(3.11)

Since the Euler expansion is valid for any ﬁeld function ψ, Ψ,,wehave,in

general, for the Lagrangian system







∂

∂t







(3.12)

3.3 An example of the use of Lagrangian coordinates 175

3.2.2 The mass-conservation equation in the Lagrangian form

We are now ready to formulate the mass-conservation or the continuity equation

in the Lagrangian form. Starting with the general coordinate-free form of the

continuity equation (M6.67) it is easy to show that, in the q

system, this equation

may be written as



√



+ ρ

√

∂ ˙q

∂q

= 0(3.13)

Setting here q

= a

, we obtain



√





∂

∂t



√





= 0(3.14)

since da

/dt = ˙a

= 0. This conservative condition is analogous, for example, to

isentropic motion dθ/dt = 0, where θ is constant along the trajectory. Integration

of (3.14) yields the Lagrangian form of the continuity equation



√





√



t=t

= constant (3.15)

This equation can be easily interpreted by realizing that the density ρ and

√

generally change with time. The quantity

√

corresponds to the scalar triple

product [a

, a

] which represents the volume of a parallelepiped. If the volume

expands (contracts) the density must decrease (increase), which is the principle of

conservation of mass.

Finally, we consider the special but interesting case that, at t = t

, the Lagrangian

and the Cartesian system are identical so that

√



= 1. In this case (3.15)

reduces to



√



= ρ(t = t

) = constant (3.16)

In case of incompressibility we have ρ = ρ(t = t

) and we obtain

√

= 1.

3.3 An example of the use of Lagrangian coordinates

3.3.1 General remarks

In order to appreciate more fully the method of Lagrangian coordinates, we will

work out an example and show how to ﬁnd the approximate numerical solution to a

176 The material and the local description of ﬂow

one-dimensional hyperbolic system involving the thermo-hydrodynamic differen-

tial equations. We refer to Chapter 12 of Richtmeyer and Morton (1967). The ﬂuid

system is assumed to be frictionless, and Coriolis effects are ignored. For simplic-

ity we disregard any subgrid heat and mass ﬂuxes as well as heat sources and the

gravitational force. The thermodynamic properties of the ﬂuid will be expressed in

the form

p = p(e, α)(3.17)

where p is the air pressure, e the speciﬁc internal energy, and α = 1/ρ the speciﬁc

volume.

If we consider an ideal gas, for which the internal energy depends on temperature

only, then (3.17) reduces to the ideal-gas law. Later the Courant–Friedrichs–Lewy

stability criterion of the numerical solution, which involves the isentropic speed of

sound c, will be discussed brieﬂy. This quantity is deﬁned by

dρ

or c = α



−

dα

(3.18)

On expanding (3.17) and replacing de with the help of the ﬁrst law of thermody-

namics, we obtain

dp =



∂p

∂e



de +



∂p

∂α



dα, de =−pdα (3.19)

and

dα

=−p



∂p

∂e





∂p

∂α



(3.20)

Therefore, the speed of sound is

c = α





∂p

∂e



−



∂p

∂α



(3.21)

We use the following notation for the ﬁnite-difference equations of the numer-

ical scheme. Let ψ(x, t) represent an arbitrary function of the spatial variable x

and time t,thenψ

stands for the ﬁnite-difference approximation ψ(jx,nt)

with x, t the discrete distances in the space-time grid. Since central-difference

approximations will be used, j and n will assume integer as well as half-integer

values.

3.3 An example of the use of Lagrangian coordinates 177

3.3.2 The thermo-hydrodynamic equations

In our ﬂow problem the Lagrangian coordinates a

of a ﬂuid particle will be

represented by the Cartesian coordinates x

at time t = t

. In the one-dimensional

case, which is considered here, we have

a = x(t

)(3.22)

Therefore, the transformation equation between the Cartesian and the Lagrangian

coordinates at the arbitrary time t is given by

x = x(a, t)(3.23)

This is the formal one-dimensional parameter representation of the trajectory where

the value of a, i.e. the Cartesian coordinate at t = t

, is constant along the trajec-

tory. Using the assumptions stated above, we obtain in Cartesian coordinates the

following thermo-hydrodynamic system:

Equation of motion:

=−α

∂p

∂x

Trajectory:

= u

Continuity equation:

dα

= α

∂u

∂x

Energy equation:

=−p

dα

Equation of state: p = p(e, α)

(3.24)

The ﬁrst equation is identical with (2.38a) if we set f = 0. Therefore, the equation

of motion refers to the absolute coordinate system.

The equations (3.24) must now be transformed into the Lagrangian coordinates.

First of all we adapt (3.15) to the present problem. From the general deﬁnition (see

(M4.21))

√



∂(x

)

∂(a

)



(3.25a)

we ﬁnd

√

∂x

∂a

∂x

∂a

with

√

= 1(3.25b)

Using (3.11) and multiplying both sides of the equation of motion by ∂x/∂a,we

obtain ﬁrst

∂x

∂a



∂u

∂t



=−α

∂p

∂a

(3.26)

178 The material and the local description of ﬂow

From (3.12) we ﬁnd the equation of the trajectory as



∂x

∂t



= u (3.27)

The continuity equation is given by (3.16), which in our case simpliﬁes to

α = α

∂x

∂a

(3.28)

With the help of the continuity equation in Lagrangian coordinates, (3.26) may be

written in the form



∂u

∂t



=−α

∂p

∂a

(3.29)

The quantity α

= α(a,t

) represents the speciﬁc volume at time t = t

of the

medium being considered. In this example we take α

= constant, for simplicity.

The energy equation transforms likewise. With the help of (3.12) we get from

the fourth equation of (3.24)



∂e

∂t



=−p



∂α

∂t



(3.30)

For ease of reference the system of equations to be solved will be collected in

(3.31):

Equation of motion:



∂u

∂t



=−α

∂p

∂a

Trajectory:



∂x

∂t



= u

Continuity equation: α = α

∂x

∂a

Energy equation:



∂e

∂t



=−p



∂α

∂t



Equation of state: p = p(e, α)

(3.31)

3.3.3 Difference approximations

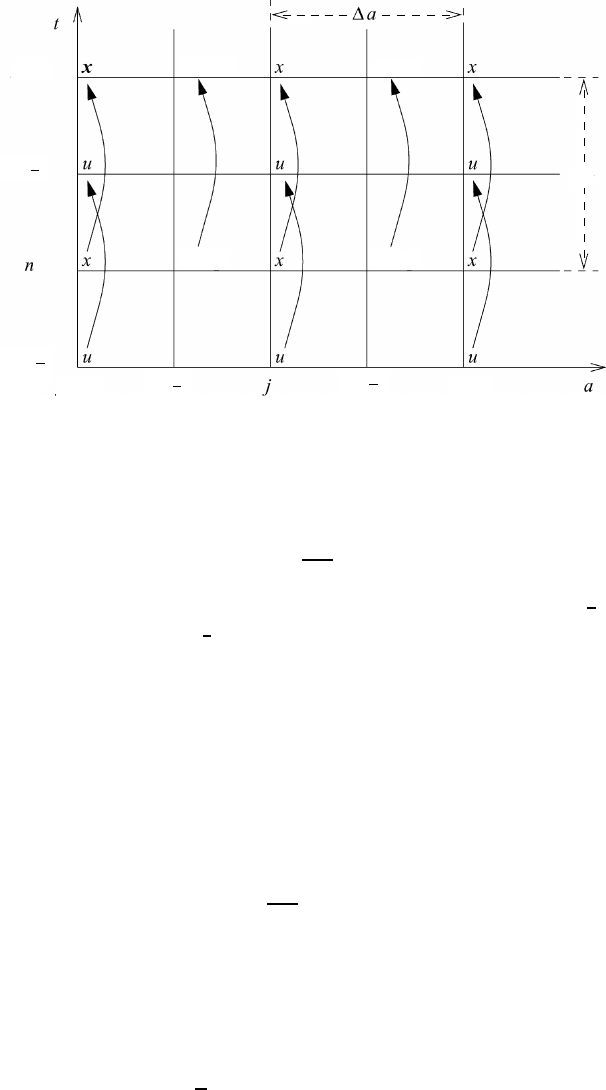
The central-difference scheme that we wish to use for the numerical approximation

of equation (3.31) is shown in Figure 3.5 together with the various quantities to be

calculated.

The arrows show the time step. If we succeed in calculating the various state

quantities at times (n +

) t and (n + 1) t from (n −

) t and nt, then the

method can be used for an arbitrary time integration using Lagrangian coordinates.

We will now discretize the equations (3.31).

3.3 An example of the use of Lagrangian coordinates 179

n + 1

j − 1 j + 1

n +

n −

j −

j +

α, e, pα, e, p

α, e, p α, e, p

∆t

Fig. 3.5 The rectangular network of grid points and discretization scheme.

Equation of motion:

n+1/2

= u

n−1/2

− α

t

a



j+1/2

− p

j−1/2



(3.32a)

Equation (3.32a) is of the explicit form. The quantity u

n+1/2

= u(a

, (n +

) t)is

the velocity at time t = (n +

) t of the trajectory T

Trajectory:

n+1

= x

+ t u

n+1/2

(3.32b)

Since u

n+1/2

is known from (3.32a), this equation is explicit also. The calculated

quantity x

n+1

represents the moving ﬂuid particle at time t = (n + 1) t of the

trajectory T

Continuity equation:

n+1

j+1/2

a



n+1

j+1

− x

n+1



(3.32c)

The values of x

n+1

and x

n+1

j+1

are considered known so that (3.32c) is explicit also.

The quantity α

n+1

j+1/2

is the speciﬁc volume at time t = (n + 1) t of the trajectory

j+1/2

Energy equation:

n+1

j+1/2

= e

j+1/2

−



j+1/2

+ p

n+1

j+1/2



n+1

j+1/2

− α

j+1/2



(3.32d)

180 The material and the local description of ﬂow

Using the equation of state

n+1

j+1/2

= p



n+1

j+1/2

,α

n+1

j+1/2



(3.32e)

and replacing the term p

n+1

j+1/2

results in the only implicit difference equation

n+1

j+1/2

= e

j+1/2

−



j+1/2

+ p



n+1

j+1/2

,α

n+1

j+1/2



n+1

j+1/2

− α

j+1/2



(3.32f )

Since α

n+1

j+1/2

is known from (3.32c), only e

n+1

j+1/2

needs to be determined, but it

also occurs on the right-hand side of the equation. Therefore, we must proceed

iteratively to ﬁnd e

n+1

j+1/2

, which is the speciﬁc internal energy at time t = (n +1) t

of the trajectory T

j+1/2

It should be noted that the difference equations must be solved in the given

order. The required state quantities can be determined explicitly, except for the

speciﬁc internal energy, which must be found iteratively for each nt and at

each grid point (j +

). Instead of (3.32f) we could also use a simpler explicit

version of the difference equation, but this would decrease the numerical reliability

of the scheme. In the ﬁnite-difference scheme adopted all other ﬁnite-difference

equations use central differences so that, for each point in the (a, t)-plane, the partial

derivatives are approximated to second-

order accuracy

O(t

)andO(a

Some schematic model results are shown in Figure 3.6 for a section of the space-

time grid beginning with time t = t

. The trajectories of the various particles are

labelled according to their positions at time t = t

. Therefore, the trajectory T

traces the path of the particle whose Lagrangian coordinate is a

as described by

= x(a

,t), where a

is the value x

of the trajectory at time t = t

3.3.4 Initial values and boundary conditions

The initial time t = t

is taken at n = 0. At this time, at all gridpoints j the

initial values of the trajectories x

= a

must be known according to (3.22).

At all points between j − 1,j,j + 1, i.e. at j −

,j +

etc., initial values of

α, e, p must be available also. Additionally, for time t =−t/2 all velocities

u(x

, −t/2),j = 0, 1,...,J must be given.

An interpolation scheme can be used to ﬁnd the still-missing initial values

−1/2

= u(a

, −t/2) = u(x

, −t/2) on the trajectory T

to start the calculations.

3.3.4.1 Approximate determination of u

1/2

and x

Using (3.32a) and (3.32b) and the given gridpoint value u(x

, −t/2) we initially

estimate the values (indicated by the tilde)

u

1/2

= u(x

, −t/2) − α

t

a



j+1/2

− p

j−1/2



x

= x

+ t u

1/2

(3.33)