Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

1.6 The decomposition of the equation of motion 151
Next we need to specifiy the general gradient operator:
∇=q
n
∂
∂q
n
= e
1
g
11
∂
∂q
1
+ e
2
g
22
∂
∂q
2
+ e
3
g
33
∂
∂q
3
(1.74)
which, in the coordinate system being considered, is easily converted to the form
∇=e
λ
1
r cos ϕ
∂
∂λ
+ e
ϕ
1
r
∂
∂ϕ
+ e
r
∂
∂r
= e
λ
∂
∂λ
*
+ e
ϕ
∂
∂ϕ
*
+ e
r
∂
∂z
with
∂
∂λ
*
=
1
r cos ϕ
∂
∂λ
,
∂
∂ϕ
*
=
1
r
∂
∂ϕ
,
∂
∂z
=
∂
∂r
(1.75)
The relative velocity is simply found by dividing (1.72b) by dt, which results in
v =
dr
dt
= r cos ϕ
˙
λe
λ
+ r ˙ϕe
ϕ
+ ˙re
r
= ue
λ
+ ve
ϕ
+ we
r
with u
*
i
=
√
g
ii
˙q
i
,u
*
1
= u, u
*
2
= v, u
*
3
= w
(1.76)
In (1.76) the contravariant velocities
˙
λ, ˙ϕ, ˙r have been converted into physical
measure numbers u
*
i
.Thelocal velocity dyadic is then given by
∇v =
e
λ
1
r cos ϕ
∂
∂λ
+ e
ϕ
1
r
∂
∂ϕ
+ e
r
∂
∂r
(ue
λ
+ ve
ϕ
+ we
r
)(1.77)
By employing the formulas (M4.45) for the partial derivatives of the unit vectors
in the spherical system, we find the following relationships:
∂v
∂λ
=
∂u
∂λ
e
λ
+ u(sin ϕ e
ϕ
− cos ϕ e
r
) +
∂v
∂λ
e
ϕ
− v sin ϕ e
λ
+
∂w
∂λ
e
r
+ w cos ϕ e
λ
∂v
∂ϕ
=
∂u
∂ϕ
e
λ
+
∂v
∂ϕ
e
ϕ
− ve
r
+
∂w
∂ϕ
e
r
+ we
ϕ
∂v
∂r
=
∂u
∂r
e
λ
+
∂v
∂r
e
ϕ
+
∂w
∂r
e
r
(1.78)
Using the above formulas it is almost trivial to find the three components of the
advection term. The results are
e
λ
· (v ·∇v) =
u
r cos ϕ
∂u
∂λ
+
v
r
∂u
∂ϕ
+ w
∂u
∂r
+
uw
r
−
uv
r
tan ϕ
e
ϕ
· (v ·∇v) =
u
r cos ϕ
∂v
∂λ
+
v
r
∂v
∂ϕ
+ w
∂v
∂r
+
vw
r
+
u
2
r
tan ϕ
e
r
· (v ·∇v) =
u
r cos ϕ
∂w
∂λ
+
v
r
∂w
∂ϕ
+ w
∂w
∂r
−
1
r
(u
2
+ v
2
)
(1.79)
152 The laws of atmospheric motion
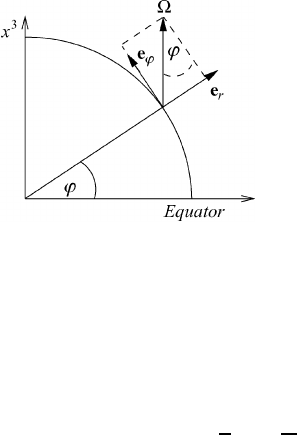
Fig. 1.4 Decomposition of the angular velocity vector.
In order to find the components of the Coriolis force, we need to decompose
the angular velocity vector which is oriented perpendicular to the equatorial plane;
see Figure 1.2. Therefore, the angular velocity has no component parallel to the
equatorial plane, as is shown in Figure 1.4. The result is
Ω = cos ϕ e
ϕ
+ sin ϕ e
r
=
l
2
e
ϕ
+
f
2
e
r
(1.80)
with
l = 2 cos ϕ, f = 2 sin ϕ (1.81)
so that
2Ω × v = (lw − fv)e
λ
+ fue
ϕ
− lue
r
(1.82)
The terms f and l are the so-called Coriolis parameters.
According to our previous discussion, the relation between the acceleration of
gravity and the geopotential is given by
g =−∇φ =−∇(φ
a
+ φ
z
)(1.83a)
Approximating surfaces of φ = constant by spherical surfaces, this equation
reduces to
∇φ = e
r
g (1.83b)
According to (1.43) the centrifugal potential depends on the distance R from the
earth’s axis. Therefore, g depends on the geographical latitude as well as on the
vertical distance from the earth’s surface; see Figure 1.2. For most meteorological
purposes the height dependence of g may be safely ignored so that g = g(ϕ).
However, the latitudinal dependence of g is also relatively weak, yielding values
in the range of 9.780 m s
−2
≤ g ≤ 9.832 m s
−2
at the equator and the North pole,
respectively. Therefore, the ϕ-dependence of g is usually not explicitly consid-
ered in the equation of motion. Instead of this, g is assigned a constant value of
9.81 m s
−2
. A more complete discussion of this subject may be found, for example,
in TH.
1.6 The decomposition of the equation of motion 153
Above the planetary boundary layer, which extends to about 1 km in height,
frictional effects may often be ignored. For this situation the component form of
the equation of motion in spherical coordinates is easily obtained from (1.71) by
utilizing (1.79), (1.82), and (1.83) and is given by
∂u
∂t
+
u
∂u
∂λ
*
+ v
∂u
∂ϕ
*
+ w
∂u
∂z
+
uw
r
−
uv
r
tan ϕ + lw − fv+
1
ρ
∂p
∂λ
*
= 0
12 345678
∂v
∂t
+
u
∂v
∂λ
*
+ v
∂v
∂ϕ
*
+ w
∂v
∂z
+
vw
r
+
u
2
r
tan ϕ + fu+
1
ρ
∂p
∂ϕ
*
= 0
12 34578
∂w
∂t
+
u
∂w
∂λ
*
+ v
∂w
∂ϕ
*
+ w
∂w
∂z
−
1
r
(u
2
+ v
2
) −lu +
1
ρ
∂p
∂z
+ g = 0
12 34689
(1.84)
Let us briefly discuss the various terms appearing in (1.84), which are numbered
for ease of reference. These terms represent either real or fictitious forces. In each
equation term 1 is the local rate of change with time of the velocity component.
Terms 2 and 3 denote horizontal and vertical advection, respectively. Fictitious or
apparent forces do not result from the interaction of an air parcel with other bodies,
but stem from the choice of the rotating coordinate system. Terms 4 and 5 are such
apparent forces per unit mass. They are also known as metric accelerations,which
result from the curvature of the coordinate lines. The metric acceleration or metric
force per unit mass is perpendicular to the relative velocity as follows from
uw
r
−
uv
r
tan ϕ
e
λ
+
vw
r
+
u
2
r
tan ϕ
e
ϕ
−
u
2
+ v
2
r
e
r
·(ue
λ
+ve
ϕ
+we
r
) = 0
(1.85)
so these forces do not perform any work. Terms 6 and 7 are the Coriolis terms
which result from the rotation of the coordinate system. By proceeding as in (1.85)
we can again verify that the Coriolis force does not perform any work either.
Term 8 is the pressure-gradient force and term 9 denotes the acceleration due to
gravity.
Equations (1.84) are so general that they describe all scales of motion including
local circulations as well as large-scale synoptic systems. For the present, let us
consider the motion of dry air only for simplicity. Whenever we introduce moisture
with associated phase changes, the situation becomes very involved.
154 The laws of atmospheric motion
Let us now count the number of dependent variables of the atmospheric system.
These are the three velocity components u, v, w, the temperature T , the air density
ρ, and pressure p. In order to evaluate these, we must have six equations at our
disposal. These are the three component equations of motion for u, v, w,thefirst
law of thermodynamics for T , the continuity equation for ρ, and the ideal-gas law
for p. We have just as many equations as unknowns, so we say that this system
is closed. We call this system the molecular system or the nonturbulent system.In
contrast, the so-called microturbulent system, which we have not yet discussed, is
not closed, so there are more unknown quantities than equations. This necessitates
the introduction of closure assumptions.
If we compare the numerical values of the various terms appearing in the system
(1.84), we find that they may differ by various orders of magnitude. For a particular
situation to be studied, it seems reasonable to omit the insignificant terms. There
exists a systematic method for deciding how to eliminate these. This method is
known as scale analysis and will be described in the next chapter.
1.7 Problems
1.1: Show that
D
Dt
(ρv
) = ρΩ × v − ρ ∇
v
2
2
d
dt
(∇ψ) =∇
dψ
dt
−∇v·∇ψ
where ψ is an arbitrary scalar field function.
1.2:
(a) Show that
dr·(Ω × v) =
d
dt
S
dS·Ω
(b) By utilizing this equation, show that, for frictionless motion, equation (1.62)
can be written in the form
dC
dt
=−2
dS
dt
−
1
ρ
d
g
p with C =
dr·v
where S
is the projection of the material surface S(t) on the equatorial plane.
1.3: In the absolute system the frictional tensor
J(v
A
) is given by (1.12).

1.7 Problems 155
(a) Show in a coordinate-free manner that, for the rigidly rotating earth, we may
write
∇·
J(v
A
) =∇·J(v)
(b) Calculate the influence of the frictional force on the velocity profiles
v
1
(z) = C
1
ln
z
z
0
i and v
2
(z) = C
2
zi
where C
1
,C
2
,andz
0
are constants.
1.4: An incompressible fluid is streaming through a pipe of arbitrary but constant
cross-section. Along the axis of the cylinder which is pointing in the x-direction,
the fluid velocity is u =
|
v
|
everywhere so that u depends on the coordinates y and
z only.
(a) Show that the continuity equation is satisfied.
(b) Find the Navier–Stokes equation for u. Ignore gravity and any convective
motion.
(c) Find a solution for u if the pipe is a circular cylinder of radius R
0
. The boundary
condition is u = 0atR = R
0
. Use cylindrical coordinates.
(d) Find the amount Q of fluid streaming through the cross-section of the cylinder
per unit time.
1.5: The continuity equation for relative motion can be written in the form
d
dt
ρ
√
g
q
+ ρ
√
g
q
∂ ˙q
n
∂q
n
= 0
Show that this equation is identical with (1.50).
1.6: Draw and discuss the energy-transformation diagram corresponding to (1.69).
1.7: Show the validity of the following equation:
D
Dt
(ρφ) =
∂ρφ
∂t
x
i
+∇·(ρv
A
φ) =
1
√
g
q
∂
∂t
√
g
q
ρφ
q
i
+
∂
∂q
n
√
g
q
ρφ ˙q
n

156 The laws of atmospheric motion
1.8: Use equations (M4.42) and (M4.45) to verify the following relations for the
unit vectors (e
λ
, e
ϕ
, e
r
) of the geographical coordinate system:
∂e
λ
∂λ
= e
ϕ
sin ϕ − e
r
cos ϕ,
∂e
λ
∂ϕ
= 0,
∂e
λ
∂r
= 0
∂e
ϕ
∂λ
=−e
λ
sin ϕ,
∂e
ϕ
∂ϕ
=−e
r
,
∂e
ϕ
∂r
= 0
∂e
r
∂λ
= e
λ
cos ϕ,
∂e
r
∂ϕ
= e
ϕ
,
∂e
r
∂r
= 0
∂e
λ
∂t
= Ω × e
λ
=
∂e
λ
∂λ
,
∂e
ϕ
∂t
= Ω × e
ϕ
=
∂e
ϕ
∂λ
,
∂e
r
∂t
= Ω × e
r
=
∂e
r
∂λ
where Ω = (cos ϕ e
ϕ
+ sin ϕ e
r
).

2
Scale analysis
Scale analysis is a systematic method of comparing the magnitudes of the various
terms in the hydrodynamical equations describing the atmospheric motion. This
theory is instrumental in the design of consistent dynamic–mathematical models
for dynamic analysis and numerical weather prediction. Charney (1948) introduced
this technique to large-scale dynamics and showed that it is not necessary to
use the complete scalar set of Navier–Stokes equations to describe the synoptic
and planetary-scale motion. Among others, mainly Burger (1958) and Phillips
(1963) used and extended this method. For additional details and a more complete
bibliography see Haltiner and Williams (1980). In this chapter we follow Pichler’s
(1997) excellent introduction to scale analysis.
2.1 An outline of the method
Scale analysis makes it possible to objectively estimate the magnitudes of the
various terms in an equation describing a physical system. The basic idea is to
formulate a simplified equation by ignoring certain terms in a consistent manner
without changing the basic physics. Let us consider an equation of the form
ψ
1
+ ψ
2
+···+ψ
i
+···+ψ
n
= 0(2.1)
which may be a part of a more general system. The task ahead is to estimate the
magnitudes of the individual terms in (2.1). Let us define the magnitude of each
term by the symbol
ψ
i
m
= magnitude of ψ
i
(2.2)
From (2.1) and (2.2) we form a dimensionless expression
ψ
i
=
ψ
i
ψ
i
m
(2.3)
157

158 Scale analysis
which by necessity is of magnitude 1. In order to avoid confusion in the notation
we have added the suffix m within the bracket in (2.2) to remind the reader that
this bracket refers to the magnitude of the term. With (2.3) equation (2.1) can be
written as
ψ
1
m
ψ
1
+
ψ
2
m
ψ
2
+···+
ψ
i
m
ψ
i
+···+
ψ
n
m
ψ
n
= 0(2.4)
In order to consistently compare the magnitude of the various terms we introduce
dimensionless characteristic numbers defined by
ψ
r,i
=
ψ
r
m
ψ
i
m
(2.5)
The importance of one particular term, say term i in (2.1), will now be investigated.
We divide equation (2.4) by the magnitude of term i and find, using the definition
of the characteristic numbers, the expression
ψ
1,i
ψ
1
+ ψ
2,i
ψ
2
+···+
ψ
i
···+ψ
n,i
ψ
n
= 0(2.6)
If, for example, all characteristic numbers are much larger than 1, which is the
number multiplying term i,thentermi has no significance in relation to the
remaining terms and may be ignored. If, on the other hand, all characteristic
numbers are much smaller than 1, then term i plays a dominant role and must be
considered in the physical treatment under all circumstances.
We will now apply this method to the Navier–Stokes equation (1.71) which
excludes the deformational velocity v
D
. In the form (2.4) the Navier–Stokes equa-
tion can then be written as
∂v
∂t
q
i
m
∂v
∂t
q
i
+ [ v ·∇v ]
m
v ·∇v
+
1
ρ
∇p
m
1
ρ
∇p
+ [ ∇φ ]
m
∇φ
+ 2[ Ω × v ]
m
Ω × v
−
1
ρ
∇·
J
m
1
ρ
∇·
J
= 0
(2.7)
This is a very convenient form in which to introduce various characteristic numbers
that have proven to be very useful in the study of fluids and gases. Of particular
interest is the relation of the magnitude of the individual terms to the inertial force
per unit mass [ v ·∇v ]
m
. We proceed by dividing the inertial force by the magnitudes

2.2 Practical formulation of the dimensionless flow numbers 159
of each of the remaining terms. Thus, we obtain five dimensionless numbers:
the Strouhal number: St =
[ v ·∇v ]
m
∂v
∂t
q
i
m
the Euler number: Eu =
[ v ·∇v ]
m
1
ρ
∇p
m
the Froude number: Fr =
[ v ·∇v ]
m
[ ∇φ ]
m
the Rossby number: Ro =
[ v ·∇v ]
m
2[ Ω × v ]
m
the Reynolds number: Re =
[ v ·∇v ]
m
1
ρ
∇·
J
m
(2.8)
Each of these numbers expresses the ratio of the magnitude of the inertial force
to one of the remaining forces appearing in the Navier–Stokes equation. These
numbers are the reciprocals of the characteristic numbers defined by (2.5). By
inserting the numbers in (2.8) into (2.7) we obtain the dimensionless form of the
Navier–Stokes equation:
1
St
∂v
∂t
q
i
+
v ·∇v
+
1
Eu
1
ρ
∇p
+
1
Fr
∇φ
+
1
Ro
Ω × v
−
1
Re
1
ρ
∇·
J
= 0
(2.9)
The characteristic number of the second term in (2.9) equals 1. If, for example,
the remaining characteristic numbers are much larger than 1, then the inertial force
may be ignored in comparison with the other forces appearing in (2.9). This means
that the nonlinear equation (2.9) in this special case reduces to a linear partial
differential equation. Inspection of (2.9) shows that the frictional term is important
only if the Reynolds number is very small.
2.2 Practical formulation of the dimensionless flow numbers
Equation (2.8) is a collection of various important flow numbers. For practical
applications these flow numbers must be expressed in terms of easily accessible
160 Scale analysis
variables characterizing the flow field. The basic variables required are time, the
wind speed, the angular velocity of the earth, the acceleration due to gravity,
pressure, density, and temperature. The scale of motion is characterized by the
horizontal (L
1
,L
2
) and vertical (L
3
) length scales of the phenomena to be
investigated. The synoptic scale of motion refers to long waves, low- and high-
pressure systems so that L
1
,L
2
≥ 10
6
m. The vertical scale L
3
includes the
weather-effective part of the atmosphere and may be approximated by L
3
≈ 10
4
m.
According to equation (2.3) we introduce the length scale x by means of
x = [ x ]
m
x
= S
x
(2.10)
Utilizing this expression, the nabla operator may be written as
∇=[ ∇ ]
m
∇
=
1
S
∇
(2.11)
The time scale will be expressed in terms of the local characteristic time interval T
l
describing the nonstationary motion. If the magnitude of the phase velocity of the
wave (pressure system) is denoted by C, then we replace the time t by means of
t = [ t ]
m
t
= T
l
t
=
S
C
t
(2.12)
Likewise, we write for the remaining variables
1
ρ
=
1
ρ
m
1
ρ
= A
1
ρ
,p=
p
m
p
= P
p
,T= [ T ]
m
T
= T
0
T
v = [ v ]
m
v
= V
v
, Ω =
Ω
, ∇φ = G
∇φ
, [
J ]
m
=
µ
0
V
S
(2.13)
The characteristic magnitudes of pressure, density, and temperature are related by
the ideal-gas law
AP = R
0
T
0
(2.14)
where R
0
is the gas constant of dry air. Effects of moisture on temperature are
considered unimportant and are omitted. With the help of the definitions (2.13)
the magnitudes of all terms occurring in the Navier–Stokes equation (2.7) can now
be written as
∂v
∂t
q
i
m
=
V
T
l
, [ v ·∇v ]
m
=
V
2
S
,
1
ρ
∇p
m
=
AP
S
=
R
0
T
0
S
[ ∇φ ]
m
= G, [2Ω × v ]
m
= 2V ,
1
ρ
∇·J
m
=
Aµ
0
V
S
2
(2.15)
