Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

M7.2 Two-dimensional ﬂow 121

Fig. M7.12 Phase portraits for the stable and the unstable spiral.

From the previous examples we recognize that the type of the eigenvalue de-

termines the stabililty behavior of the ﬁxed point. The essential information is

collected in the table of Figure M7.13. This table can be used to construct the

stability diagram shown in the ﬁgure. In this diagram the ordinate is the trace τ

and the abscissa is the determinant  of the matrix A of the two-dimensional

linear system. Saddle points, nodes, and spirals occur in the large open regions

of the (,τ)-plane. They are the most important ﬁxed points. Inspection of

Figure M7.13 shows that centers, stars, and degenerate nodes are borderline cases.

Of these special cases, centers are by far the most important since they occur in

energy-conserving frictionless mechanical systems.

M7.2.3 Two-dimensional nonlinear systems

Before proceeding we state without proof that different trajectories do not intersect.

This information may be extracted from the existence and uniqueness theorem of

differential equations. If trajectories were to intersect, then there would be two

solutions starting from the same point, the crossing point. This would violate the

uniqueness part of the theorem. Because of the fact that trajectories do not intersect,

we may expect that phase portraits have a “well-groomed” look to them.

By linearizing two-dimensional systems, it is often possible to obtain an approx-

imate phase portrait near the ﬁxed points. The general form of the nonlinear system

is given by

˙x = f

(x,y), ˙y = f

(x,y)or

x = f(x)(M7.16)

We assume the existence of a ﬁxed point (x

∗

)sothatf

∗

) = 0and

∗

) = 0. Let u = x − x

∗

and v = y − y

∗

represent the components of a

small perturbation from the ﬁxed point. To see whether the perturbation grows or

is damped out, we need to obtain differential equations for ˙u = ˙x and ˙v = ˙y.

122 Introduction to the concepts of nonlinear dynamics

centers

saddle

oints

stable spirals

stars, degenerate nodes

unstable spirals

stable nodes

unstable nodes

− 4∆ = 0

∆

1,2

ττ

− 4 Fixed points

Real, distinct, opposite signs <00 >0 (Unstable) saddle points

Real, distinct, >0 >0 >0 >0 Unstable nodes

Real, distinct, <0 >0 <0 >0 Stable nodes

Complex conjugate,

real parts

>0 <0 <0

Stable spirals

Complex conjugate,

real parts

>0 >0 <0

Unstable spirals

Purely imaginary

>00 <0 (Stable) centers

Real, λ

= λ

< 0 >0 <00Stable nodes

, star-shaped

Real,

= λ

> 0 >0 >00Unstable nodes, star-shaped

Fig. M7.13 General classiﬁcation of ﬁxed points of the two-dimensional linear system

 = λ

, τ = λ

+ λ

Expanding f

and f

in a two-dimensional Taylor series we ﬁnd

∗

+ u, y

∗

+ v) = f

∗

) + u

∂f

∂x



∗

+ v

∂f

∂y



∗

+O(u

,uv),

i = 1, 2

(M7.17)

The series will be discontinued after the linear terms since the quadratic terms

O(u

,uv) are very small and will be ignored. Because f

∗

)andf

∗

)

are zero, the linearized system may be written as





˙u

˙v





= A









,A=







∂f

∂x

∂f

∂y

∂f

∂x

∂f

∂y







∗

(M7.18)

where A is the Jacobian matrix at the ﬁxed point. The dynamics can now be

analyzed by means of the procedures discussed above.

M7.2 Two-dimensional ﬂow 123

The question of whether the linearization of the nonlinear system gives the

correct qualitative picture of the phase portrait near the ﬁxed point (x

∗

) arises.

This is indeed the case as long as the ﬁxed point is not located on one of the border

lines shown in Figure M7.13.

We will demonstrate the linearization procedure by ﬁnding and classifying the

ﬁxed points of the following example

˙x =−x + x

, ˙y =−2y (M7.19)

The ﬁxed points occur where ˙x = 0, ˙y = 0 simultaneously. The system is

uncoupled so that the ﬁxed points are easily found: (x

∗

) = (0, 0), (1, 0), (−1, 0).

The Jacobian matrix is given by

A =





− 1 + 3x

0 − 2





∗

(M7.20)

Thus, for the three ﬁxed points we ﬁnd

∗

= 0,y

∗

= 0): A =





− 10

0 − 2





,τ=−3,= 2

∗

=±1,y

∗

= 0): A =





0 − 2





,τ= 0,=−4

(M7.21)

They are shown in Figure M7.14. On consulting the stability diagram of

Figure M7.13 we may conclude that the ﬁxed points represent the stable node

at the origin and two unstable saddle points P

. Since we are not treating

borderline cases we can be sure that our result is correct.

Fig. M7.14 The stability diagram for the ﬁxed points of the example (M7.19).

124 Introduction to the concepts of nonlinear dynamics

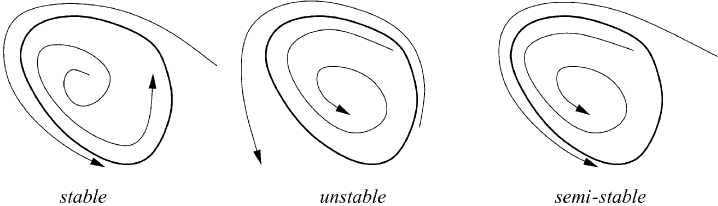
Fig. M7.15 Stable, unstable, and semi-stable limit cycle.

M7.2.4 Limit cycles

Let us now consider a limit cycle, which is a different type of a ﬁxed point. By

deﬁnition, a limit cycle is an isolated closed trajectory. In this context isolated

implies that neighboring trajectories are not closed. They spiral either toward or

away from the limit cycle, as shown in Figure M7.15. In the stable case the

limit cycle is approached by all neighboring trajectories. Thus, the limit cycle is

attracting. In the unstable situation the neighboring trajectories are repelled by the

limit cycle. Finally, the rare case of a semi-stable limit cycle is a combination of

the ﬁrst two possibilities.

Let us consider the simple example

˙r = r(1 − r

θ = 1(M7.22)

where the dynamic system refers to polar coordinates (r, θ )withr>0. The radial

and angular equations are uncoupled so they may be handled independently. We

treat the ﬂow as a vector ﬁeld on the line r. The ﬁxed points are r

∗

= 0and

∗

= 1. They are, respectively, unstable and stable. We observe that the equation of

a unit circle r

= x

= 1 represents a closed trajectory in the phase plane; see

Figure M7.16. Since we are dealing with constant angular motion, we should expect

that all trajectories spiral toward the limit cycle r = 1. We will soon return to this

problem.

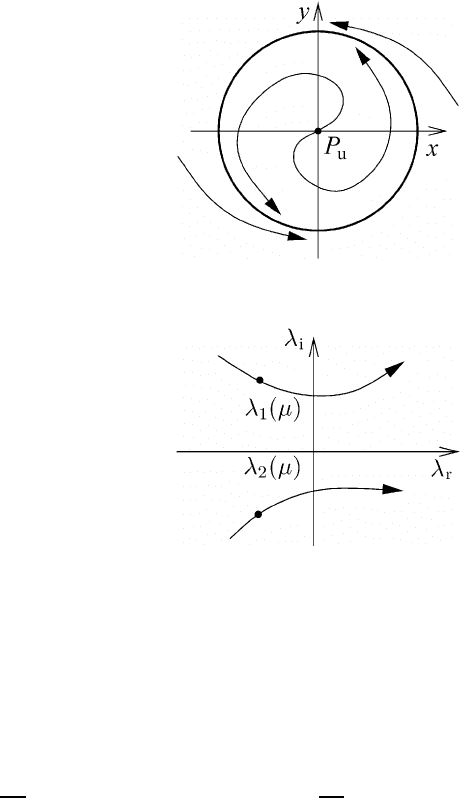
M7.2.5 Hopf bifurcation

Some bifurcations generate limit cycles or other periodic solutions. One such type

is known as the Hopf bifurcation. Let us assume that a two-dimensional system has

a stable ﬁxed point. Now the question of in which ways the ﬁxed point could lose

stability if the stability parameter µ is varied arises. The position of the eigenvalues

of the Jacobian matrix in the complex plane will provide the answer. Since the ﬁxed

point is stable by assumption, the two eigenvalues λ

1,2

= λ

± iλ

have negative

M7.2 Two-dimensional ﬂow 125

Fig. M7.16 The limit cycle corresponding to

equation (M7.22).

Fig. M7.17 Stability behaviors of the eigenvalues λ

1,2

as functions of the stability param-

eter µ.

real parts and must therefore lie in the left-hand half of the complex plane. In order

to destabilize the ﬁxed point, one or both of the eigenvalues must move into the

right-hand half of the complex plane as µ varies; see Figure M7.17.

As an example let us consider the second-order nonlinear system

=−ωy + (µ − x

− y

)x,

= ωx + (µ − x

− y

)y (M7.23)

where µ and ω are real constants. The only ﬁxed point is (x

∗

) = (0, 0) so that

the Jacobian matrix at the ﬁxed point is expressed by

A =





− 3x

+ µ − y

− ω − 2xy

ω − 2xy − 3y

+ µ





∗

=0,y

∗





µ − ω

ωµ





(M7.24)

The eigenvalues to this matrix are complex:

1,2

= µ ± iω (M7.25)

126 Introduction to the concepts of nonlinear dynamics

Thus we ﬁnd

τ = λ

+ λ

= 2µ,  = λ

= µ

+ ω

> 0,τ

− 4<0(M7.26)

From the stability diagram of Figure M7.13 we recognize that the ﬁxed points are

spirals. If µ<0 the spiral (often also called a focus) is stable, whereas for µ>0

the spiral is unstable.

We are going to conﬁrm this conclusion since the system (M7.23) can be solved

analytically by employing polar coordinates

x = r cos θ, y = r sin θ =⇒ x + iy = r exp(iθ)(M7.27)

from which it follows that



r exp(iθ)



+ i



+ ir

dθ



exp(iθ)



ωri + (µ − r



exp(iθ)

(M7.28)

Here use of (M7.23) and (M7.27) has been made. On separating the real and

imaginary parts we ﬁnd

= r(µ − r

dθ

= ω (M7.29)

where ω is the frequency of the inﬁnitesimal oscillations. By setting ω = 1and

µ = 1 we revert to the problem (M7.22) of the previous section which led to the

introduction of the limit cycle.

The system (M7.29) is decoupled so that it is not so difﬁcult to obtain an

analytic solution. In general, it is impossible to ﬁnd analytic solutions to nonlinear

differential equations. Dividing (M7.29) by r

and setting n = r

−2

yields

+ 2µn = 2(M7.30)

Multiplication of this equation by the integrating factor exp(2µt) and integration

gives





exp(2µt) n(t)



dt = 2



exp(2µt) dt (M7.31)

from which it follows that

n(t) =

+ C exp(−2µt) with C = n(0) −

,n(0) =

(M7.32)

M7.2 Two-dimensional ﬂow 127

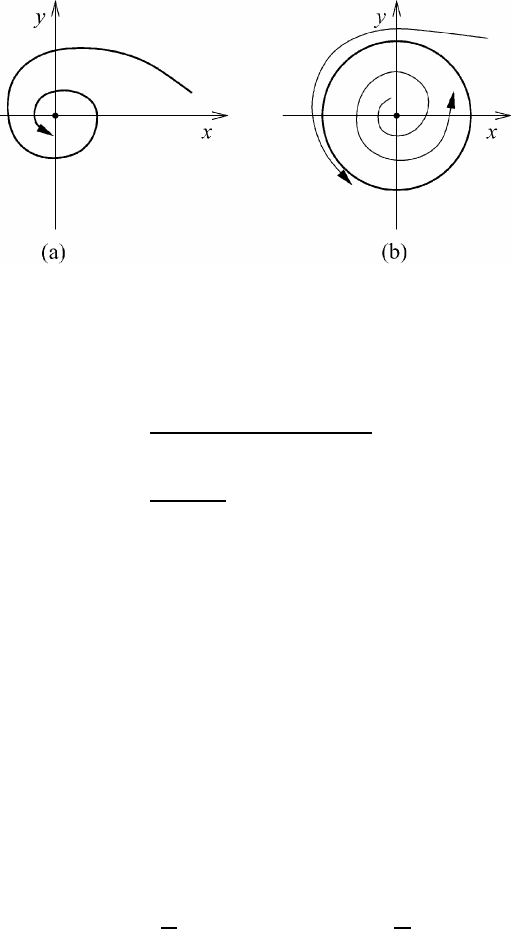
Fig. M7.18 Hopf bifurcation. (a) For µ ≤ 0 the origin is a stable spiral. (b) For µ>0

the origin is an unstable spiral. Th

e circular limit cycle at

= µ is stable.

Replacing n by r

−2

and n(0) by r

−2

gives the solution of the differential system

(M7.29):

(t) =











µr

+ (µ − r

)exp(−2µt)

µ = 0

1 + 2r

µ = 0

θ(t) = ωt + θ

(M7.33)

We will now present the phase portrait in the (x,y)-plane. As t increases from

zero to inﬁnity, we ﬁnd that, for µ ≤ 0, a stable spiral is generated, as shown in

Figure M7.18(a). This veriﬁes our previous conclusion, which was derived from

the linear stability analysis. In other words, all solutions x = [x(t),y(t)] tend to

zero as t approaches inﬁnity. Thus, each trajectory or orbit spirals into the origin.

The sense of the rotation depends on the sign of ω. We observe that, for µ = 0, the

linear stability analysis wrongly predicts a center at the origin.

For µ>0 the origin becomes an unstable focus, see Figure M7.18(b). A new

stable periodic solution arises as µ increases through zero and becomes positive.

This is the limit cycle r

= µ. Two trajectories starting inside and outside of the

limit cycle are shown in Figure M7.18(b). Since x

= µ, the solution is given

+ y

= µ or x =

√

µ cos(t + θ

),y=

√

µ sin(t + θ

)(M7.34)

This is an example of a Hopf bifurcation. Hopf (1942) showed that this type of

bifurcation occurs quite generally for systems (n>2) of nonlinear differential

equations. For further details see, for example, Drazin (1992). In the previous

idealized example the limit cycle turned out to be circular. Hopf bifurcations

encountered in practice usually result in limit cycles of elliptic shape.

128 Introduction to the concepts of nonlinear dynamics

In this example, a stable spiral has changed into an unstable spiral, which is

surrounded by a limit cycle since the real part µ of the eigenvalue has crossed the

imaginary axis from left to right as µ increased from negative to positive values.

This particular type of bifurcation is called the supercritical Hopf bifurcation.

The so-called subcritical Hopf bifurcation has an entirely different character.

After the bifurcation has occurred, the trajectories must jump to a distant attractor,

which may be a ﬁxed point, a limit cycle, inﬁnity, or a chaotic attractor if three and

higher dimensions are considered. We will study this situation in connection with

the Lorenz equations.

M7.2.6 The Liapunov function

Let us consider a system

x = f(x) having a ﬁxed point at x

∗

. Suppose that we

can ﬁnd a continuously differentiable real-valued function V (x) with the following

properties:

V (x) > 0,

V (x) < 0 ∀ x = x

∗

,V(x

∗

) = 0(M7.35)

This positive deﬁnite function is known as the Liapunov function. If this function

exists, then the system does not admit closed orbits. The condition

V (x) < 0

implies that all trajectories ﬂow “downhill” toward x

∗

. Unfortunately, there is no

systematic way to construct such functions.

M7.2.7 Fractal dimensions

Fractal dimensions are characteristic of strange attractors. Therefore, it will be

necessary to brieﬂy introduce this concept. A one-dimensional ﬁgure, such as a

straight line or a curve, can be covered by N one-dimensional boxes of side length

#.IfL is the length of the line then N# = L,sowemaywrite

N(#) =





(M7.36)

Similarly, a square and a three-dimensional cube of side lengths L can be covered

N(#) =





,N(#) =





(M7.37)

Generalizing, for a d-dimensional box we obtain

N(#) =





(M7.38)

M7.2 Two-dimensional ﬂow 129

On taking logarithms we ﬁnd

d =

ln[N(#)]

ln L − ln #

(M7.39)

In the limit of small #, the term ln L can be ignored in comparison with the

second term in the denominator of (M7.39). This results in the so-called capacity

dimension d

, which is given by

=−lim

#→0

ln[N(#)]

ln #

(M7.40)

It is easy to see that the capacity dimension of a point is zero.

There are other deﬁnitions of fractional dimensions. The most important of these

is the Hausdorff dimension HD, which permits the d-dimensional boxes to vary

in size. Thus, the capacity dimension is a special case of the Hausdorff dimension.

The inequality

HD ≤ d

(M7.41)

is valid.

In large parts this chapter follows the excellent textbook on nonlinear dynamics

and chaos by Strogatz (1994).