Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


M6.3 Integral theorems 91
In the following we present some important applications of the Stokes integral
theorem. In the first example we apply (M6.21) to a very small surface element
S = S e
3
so that ∇×A may be viewed as a constant vector and the integral
on the left-hand side of (M6.21) may be replaced by ∇×A·e
3
S. This yields the
coordinate-free definition of the rotation,
∇×A · e
3
=
1
S
dr · A
(M6.23)
In the next application we consider the horizontal flow in the Cartesian coordinate
system. In this case we write the differentials dS = k dx dy and dr = i dx + j dy.
Replacing the vector A in (M6.21) by the horizontal velocity v
h
= iu + jv yields
S
∇
h
× v
h
· k dx dy =
v
h
· dr (M6.24)
or
S
∂v
∂x
−
∂u
∂y
dx dy =
S
ζdxdy=
(udx + vdy) (M6.25)
The term ζ is known as the vorticity, which turns out to be a very useful quantity in
dynamic meteorology. Equation (M6.25) relates an integral over the vorticity with
the circulation integral.
Let us close this section by giving another important example involving the
Stokes theorem. Setting in (M6.21) A = λ ∇µ,whereλ and µ are scalar field
variables such as pressure and density, the left-hand side of this equation can be
written as
S
dS ×∇·(λ ∇µ) =
S
dS ·∇×(λ ∇µ) =
S
dS ·∇λ ×∇µ (M6.26)
Next we replace the directed surface element dS by means of (M6.4). By interpret-
ing the functions λ and µ as the coordinate lines on the surface S, surrounded by
the line , we obtain
S
dS ·∇λ ×∇µ =
S
√
gq
3
·∇λ ×∇µdλdµ
=
S
√
g[q
3
, q
1
, q
2
] dλdµ =
S
dλdµ
(M6.27)
with ∇λ = q
1
, ∇µ = q
2
. The right-hand side of (M6.21) may now be written as
dr · λ ∇µ =
λd
g
µ or
dr · λ ∇µ =
dr · [∇(λµ) − µ ∇λ] =
d
g
(λµ) −
µd
g
λ =−
µd
g
λ
(M6.28)
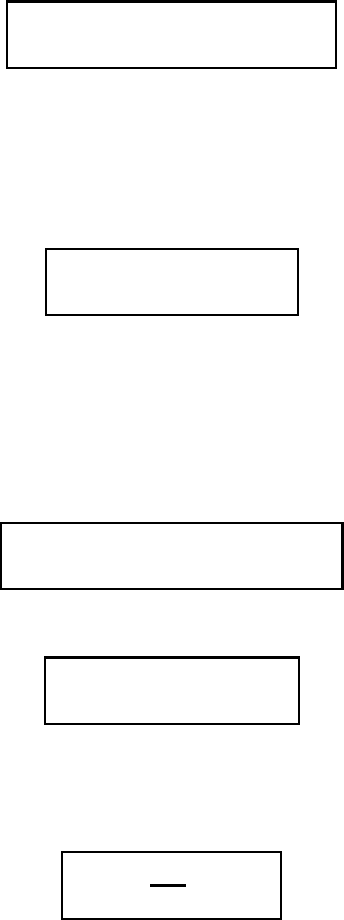
92 Integral operations
Since in general λ and µ are time-dependent functions, we have employed the geo-
metric differential d
g
defined in (M3.7), indicating that the operations are performed
at t = constant. From (M6.27) and (M6.28) we obtain the final result
S
dλdµ =
λd
g
µ =−
µd
g
λ
(M6.29)
M6.3.2 Gauss’ divergence theorem
Let us consider a closed surface S enclosing a volume V . Without proof we accept
the general integral theorem
V
dτ ∇(···) =
S
dS (···)
(M6.30)
relating a volume integral and an integral over a closed surface. In the following
we will consider various applications of equation (M6.30).
The divergence theorem due to Gauss is derived in many textbooks by employing
the Cartesian coordinate system. It is of great importance in fluid dynamics and in
many other branches of physics. The theorem is obtained by applying (M6.30) to
the field vector A and by taking the first scalar
V
dτ ∇·A =
S
dS · A =
S
A
N
dS
(M6.31)
where A
N
is the projection of A in the direction of dS. The vector of (M6.30) yields
V
dτ ∇×A =
S
dS × A
(M6.32)
Let us briefly consider some important examples. On shrinking the volume V
in (M6.31) to the differential volume element V in which ∇·A is considered
constant, this equation reduces to the coordinate-free definition of the divergence
of the vector A,
∇·A =
1
V
S
dS · A
(M6.33)
In our later studies we will often investigate two-dimensional flow fields in the
Cartesian coordinate system. In these studies we will require the application of the
two-dimensional version of the Gauss divergence theorem. Instead of deriving this
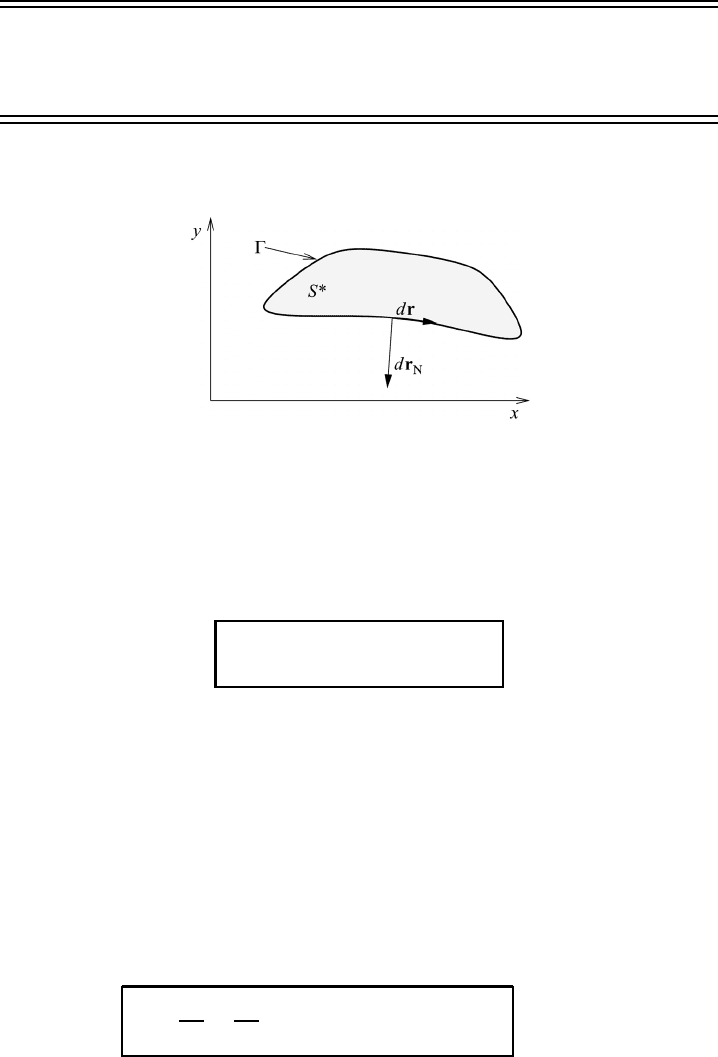
M6.3 Integral theorems 93
Table M6.1. From the three-dimensional divergence theorem of Gauss to the
two-dimensional version in Cartesian coordinates
Vo l u m e V =⇒ area S
∗
within
Volume element dτ =⇒ area element dx dy
Closed surface S =⇒ closed line
Surface element dS =⇒ line element dr
N
perpendicular to
Fig. M6.7 Explanation of the variables of the two-dimensional Gauss divergence theorem
(M6.34). dr
N
is a directed line element perpendicular to the curve .
theorem we simply employ the replacements summarized in Table M6.1. With the
help of this table we recognize that equation (M6.31) reduces to
S
∗
∇
h
· A
h
dx dy =
dr
N
· A
(M6.34)
which is the two-dimensional divergence theorem of Gauss. The terms appearing
in this equation are displayed in Figure M6.7.
In a simple but important application of (M6.34) we replace the horizontal field
vector A
h
by the horizontal velocity v
h
. We immediately obtain with dr
N
= dr ×k
S
∗
∇
h
· v
h
dx dy =
(iu + jv) · (i dy − j dx) (M6.35a)
or
S
∗
∂u
∂x
+
∂v
∂y
dx dy =
(udy − vdx) (M6.35b)
94 Integral operations
M6.4 Fluid lines, surfaces, and volumes
Let us consider a fluid in three-dimensional space whose motion is controlled by the
velocity field v(r,t)
1
.AvolumeV (t) is called a fluid volume if all surface elements
dS of the surface S enclosing V (t) are moving with the momentary velocity v(r,t)
existing at dS. Since the velocity depends on the position r and on time t,the
volume is bound to deform, thus changing size and shape.
In a first application of the concept of fluid volumes let us replace the field vector
A in (M6.31) by the velocity vector v so that this equation now reads
V
∇·v(r,t) dτ =
S
dS · v(r,t) (M6.36)
During the time increment t each surface element dS(r,t) of the volume is
covering the distance r = v(r,t) t. Thus the volume element of the difference
volume is given by
V = V (t + t) − V (t) =
S
dS · r (M6.37)
Using the mean-value theorem for integrals, (M6.36) can now be written as
∇·v =
1
V
lim
t→ 0
1
t
S
dS · r =
1
V
lim
t→0
V
t
=
1
V
dV
dt
(M6.38a)
If the volume is small enough that ∇·v is constant within V we obtain
∇·v =
1
V
dV
dt
(M6.38b)
This important expression will be applied soon.
Now we assume that V (t) consists of particles that are also moving with v(r,t).
Obviously, at all times all particles that are located on the surface of the volume
remain on the surface because their velocity and the velocity of the corresponding
surface element dS are identical. Thus no particle can leave the surface of the
volume, so the number of particles within V (t) remains constant.
Suppose that it would be possible to dye a small volume of a moving fluid
without changing its density. As we follow the motion of the dyed fluid we observe
a change of the colored part of the medium. While the original volume has changed
its shape, it is always made up of the same particles. Therefore, a fluid volume is
also called a material volume.
1
Here and in the following the velocity refers to the absolute system, that is v =v
A
. For simplicity the suffix A
has been omitted.

M6.4 Fluid lines, surfaces, and volumes 95
In analogy to the fluid or material volume we define the fluid or material surface
and the fluid or material line. As in the case of the material volume, a material
surface and a material line always consist of the same particles.
In order to efficiently describe the properties of a fluid system, we distinguish
between intensive and extensive variables. An intensive variable is a quantity
whose value is independent of the mass of the system. Examples are pressure and
temperature. The volume, on the other hand, is proportional to its mass M and is,
therefore, an example of an extensive variable. Additional examples are the kinetic
and the internal energy of the system. External variables will be denoted by .The
density of is defined by
ψ = /V .Thespecific value of is ψ = /M so
that
ψ = ρψ,whereρ = M/V is the mass density of the fluid.
Of particular interest is not the property itself but rather the change with time
of this quantity, which will now be considered. In general, any extended part of
the atmospheric continuum will be inhomogeneous so that the property of a
sizable volume V (t) must be expressed by an integral over the density
ψ = ρψ.
Since the total mass of the fluid volume is constant, the change with time of may
be easily calculated as
d
dt
=
d
dt
V (t)
ρψ dτ =
d
dt
M=constant
ψ dM
=
M=constant
dψ
dt
dM =
V (t)
ρ
dψ
dt
dτ
(M6.39)
Let us now consider a multicomponent system in which the component k has
mass M
k
and is moving with the velocity v
k
(r,t). Hence the total mass of the
system is given by
M =
N
k=0
M
k
(M6.40)
where N is the number of components. Each volume element is assumed to move
with the momentary barycentric velocity v(r,t) existing at its position r.Ifρ
k
=
M
k
/V is the density of the particle group k and ρ(r,t) is the total density, the
barycentric velocity is defined by
ρ(r,t)v(r,t) =
N
k=0
ρ
k
(r,t)v
k
(r,t) with ρ(r,t) =
N
k=0
ρ
k
(r,t) (M6.41)
Since each surface element dS of the volume is moving with the barycentric
velocity v(r,t), for the particle group k we observe a mass flux J
k
through dS,
which is known as the diffusion flux:
J
k
= ρ
k
(v
k
− v) (M6.42)

96 Integral operations
The difference between the partial velocity v
k
and the barycentric velocity v is
known as the diffusion velocity v
k,dif
= v
k
− v.
From (M6.41) and (M6.42) it is easily seen that the total mass flux through dS,
that is the sum of all diffusion fluxes, vanishes since
N
k=0
J
k
= 0(M6.43)
We conclude that the diffusion of the partial masses M
k
through the surface of the
fluid volume may change the mass composition. However, due to (M6.43), at all
times the volume conserves the total mass M.
M6.5 Time differentiation of fluid integrals
Often the analytic treatment of fluid-dynamic problems requires the time differen-
tiation of so-called fluid integrals. A fluid integral is expressed as an integral over
a fluid line, surface, or volume.
M6.5.1 Time differentiation of fluid line integrals
First we derive a formula for the total time differentiation of the fluid line integral:
d
dt
L(t)
dr · A
=
L(t)
dr ·
∂A
∂t
+
d
dt
L(t)
dr · A (M6.44)
According to the general differentiation rules for products, the total change of the
expression within the parentheses is composed of two terms. The first integral on
the right-hand side refers to the change with time of the field vector A for a line
fixed in space at time t while the second integral refers to the displacement and the
deformation of the line during the time increment t while the vector field A itself
is considered fixed in time.
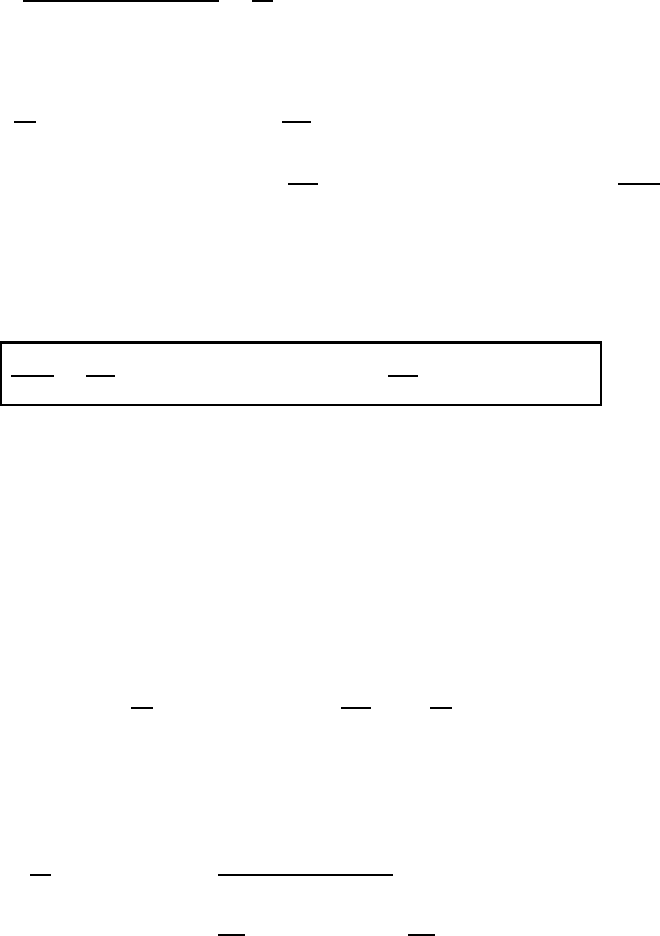
In order to evaluate the latter integral, let us consider the section (1, 2) of a line of
fluid particles at time t as shown in Figure M6.8. After the small time increment t
the particle at position 1 will have moved to 1
while the particle at position 2 has
moved to 2
. During the time increment each particle on the line increment (1, 2)
is moving the distance v t. Now we apply Stokes’ integral theorem (M6.21) to
the second integral on the right-hand side of (M6.44). According to Figure M6.8
we integrate over the area dS = dr × v t which is surrounded by the closed
curve connecting the points (1, 2, 2
, 1
, 1). Substitution of these expressions into

M6.5 Time differentiation of fluid integrals 97
Fig. M6.8 Description of the time differentiation of a fluid line integral using Stokes’
integral theorem.
(M6.21) yields
t
2
1
(dr × v) ·∇×A =
2
1
dr · A + t (v · A)
2
−
2
1
dr
· A − t (v · A)
1
=
2
1
dr · A −
2
1
dr
· A + t
2
1
d
g
(v · A)
=
2
1
dr · A −
2
1
dr
· A + t
2
1
dr ·∇(v · A)
(M6.45)
where d
g
is defined by (M3.22). On dividing this equation by t and rearranging
terms, we find in the limit t → 0
lim
t→ 0
2
1
dr
· A −
2
1
dr · A
t
=
d
dt
L(t)
dr ·A =
2
1
dr ·[(∇×A) ×v +∇(v · A)]
(M6.46)
where we have employed the rules associated with the scalar triple product. Sub-
stituting this result into (M6.44) yields for the total change with time of the fluid
line integral
d
dt
L(t)
dr · A
=
L(t)
dr ·
∂A
∂t
+ (∇×A) × v +∇(v · A)
=
L(t)
dr ·
D
1
A
Dt
(M6.47)
Here we have introduced the following differential operator for the time differen-
tiation of fluid line integrals:
D
1
A
Dt
=
∂A
∂t
+ (∇×A) × v +∇(v · A) =
dA
dt
+ (∇v) · A
(M6.48)
A special situation occurs for a closed path L(t). In this case the geometric
differential d
g
(v · A) vanishes upon integration so that (M6.47) reduces to
d
dt
L(t)
dr · A
=
L(t)
dr ·
dA
dt
−∇A · v
(M6.49)

98 Integral operations
Fig. M6.9 Time differentiation of a fluid surface integral by applying the divergence
theorem of Gauss.
M6.5.2 Time differentiation of fluid surface integrals
As in the case of the line integral, the total change of the surface integral consists
of two parts,
d
dt
S(t)
dS · A
=
S(t)
dS ·
∂A
∂t
+
d
dt
S(t)
dS · A (M6.50)
The first integral on the right-hand side describes the change with time of the field
vector A if the surface remains fixed in space at time t while the second integral
describes the displacement and the deformation of the surface while the vector field
A remains fixed in time.
In order to evaluate the latter integral we consider Figure M6.9. We first evaluate
the integral over the closed surface of the small volume and then apply the Gauss
divergence theorem (M6.31). The surface integral consists of three terms. The first
two terms are the contributions of the upper and lower surfaces while the third part
is the integration over the side surface element which is directed towards t dr×v.
Thus, we obtain
S
dS
· A −
S
dS ·A + t
(dr × v) · A =
V
∇·A dτ = t
S
(∇·A)v · dS
(M6.51)
The integration over the surface requires that all surface-element vectors must
point to the outside of the volume, which explains the negative sign of the integral
over S. The closed line integral on the left-hand side gives the contribution of
the complete side surface. This integral will be evaluated by applying the Stokes
integral theorem. On the right-hand side of (M6.51) we have replaced the volume
element dτ by t v · dS.
M6.5 Time differentiation of fluid integrals 99
Dividing (M6.51) by t and rearranging terms, in the limit t → 0 we readily
find
lim
t→ 0
S
dS
· A −
S
dS · A
t
=
d
dt
S(t)
dS · A =
S
dS ·[∇×(A × v) + v(∇·A)]
(M6.52)
Hence, equation (M6.50) may be written as
d
dt
S(t)
dS · A
=
S(t)
dS ·
∂A
∂t
+∇×(A × v) + v(∇·A)
=
S(t)
dS ·
dA
dt
+ A∇·v − v
∇·A
=
S(t)
dS ·
D
2
A
Dt
(M6.53)
Some care must be taken to evaluate the term ∇×(A×v). First we must differentiate
this expression and then we apply Grassmann’s rule. In (M6.53) we have introduced
the differential operator for the time differentiation of a fluid surface,
D
2
A
Dt
=
∂A
∂t
+∇×(A × v) +v(∇·A) =
dA
dt
+ A∇·v − v
∇·A
(M6.54)
It should be noted that (M6.48) and (M6.54) may be applied to all extensive
quantities of degree 1 and more. The last term of (M6.54) may also be written as
A ·∇v. However, for extensive functions of degree 2 and higher the corresponding
replacement is not possible since for the scalar product the commutative law is no
longer valid.
M6.5.3 Time differentiation of fluid volume integrals
Finally we consider the volume integral over the scalar field function ψ:
d
dt
V (t)
ψ dτ
=
V (t)
∂ψ
∂t
dτ +
d
dt
V (t)
ψ dτ (M6.55)
As in the previous two situations we obtain two integrals due to the differentiation
of a product. The second integral on the right-hand side will now be evaluated
according to
d
dt
V (t)
ψ dτ = lim
t→ 0
V
ψ dτ −
V
ψ dτ
t
= lim
t→ 0
1
t
V
ψ dτ = lim
t→0
1
t
S(t)
dS·v t ψ
=
S(t)
dS · (vψ) =
V (t)
∇·(vψ) dτ
(M6.56)
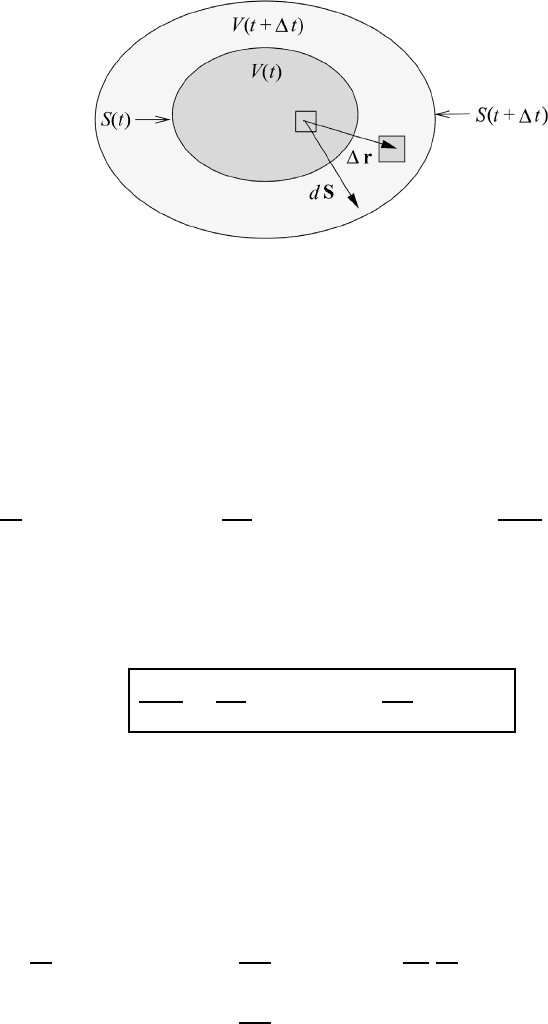
100 Integral operations
Fig. M6.10 Time differentiation of a fluid volume integral.
where V is equal to the difference volume V
− V = V (t + t) − V (t).Some
details pertaining to these formulas are shown in Figure M6.10. Inspection of this
figure shows that the volume element dτ can be replaced by dS · v t. The final
step in the derivation makes use of the Gauss divergence theorem. Thus, the total
change with time of the fluid volume integral is given by
d
dt
V (t)
ψ dτ
=
V (t)
∂ψ
∂t
dτ +∇·(vψ)
dτ =
V (t)
D
3
ψ
Dt
dτ (M6.57)
Whenever a fluid volume integral needs to be differentiated with respect to time,
we must apply the operator
D
3
ψ
Dt
=
∂ψ
∂t
+∇·(vψ) =
dψ
dt
+ ψ ∇·v
(M6.58)
This operator will be used numerous times in our studies. For reasons of simplicity
most of the time we omit the suffix 3. Similarly to the operators D
1
/Dt and D
2
/Dt,
the operator D
3
/Dt may be applied to extensive functions of any degree.
There is a shorter way to obtain equation (M6.58), which is attributed to
Lagrange:
d
dt
V (t)
ψ dτ
=
V (t)
dψ
dt
dτ +
V (t)
ψ
1
dτ
d
dt
(dτ)
dτ
=
V (t)
dψ
dt
dτ +
V (t)
ψ ∇·v dτ
(M6.59)
where use has been made of (M6.38b) by setting V = dτ.
