Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

Introduction to the concepts of nonlinear dynamics

By necessity, this introduction is brief and far from complete and may, therefore,

be reviewed in a relatively short time.

M7.1 One-dimensional ﬂow

M7.1.1 Fixed points and stability

It is very instructive to discuss a one-dimensional or ﬁrst-order dynamic system

described by the equation ˙x = f (x). Since x(t) is a real-valued function of time

t, we may consider ˙x to be a velocity repesenting the ﬂow along the x-axis. The

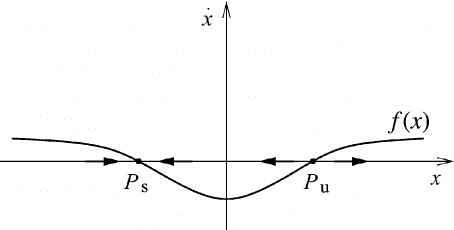
function f (x) is assumed to be smooth and real-valued. A plot of f (x) may look as

shown in Figure M7.1. We imagine a ﬂuid ﬂowing along the x-axis. This imaginary

ﬂuidiscalledthephase ﬂuid while the x-axis represents the one-dimensional phase

space.

The sign of f (x) determines the sign of the one-dimensional velocity ˙x.The

ﬂow is to the right where f (x) > 0 and to the left where f (x) < 0. The solution

of ˙x = f (x) is found by considering an imaginary ﬂuid particle, the phase

point, whose initial position is at x(t

) = x

. We now observe how this particle is

carried along by the ﬂow. As time increases, the phase point moves along the x-axis

according to some function x(t), which is called the trajectory of the ﬂuid particle.

The phase portrait is controlled by the ﬁxed points x

∗

, also known as equilibrium

or critical points, which are found from f (x

∗

) = 0. Fixed points correspond to

stagnation points of the ﬂow.

In Figure M7.1 the point P

is a stable ﬁxed point since the local ﬂow is directed

from two sides toward this point. The point P

is an unstable ﬁxed point since the

ﬂow is away from it. Interpreting the original differential equation, ﬁxed points

are equilibrium solutions. Sometimes they are also called steady, constant, or rest

solutions (the ﬂuid is stagnant or at rest). The reason for this terminology is that, if

x = x

∗

initially, then x(t) = x

∗

for all times. The deﬁnition of stable equilibrium

111

112 Introduction to the concepts of nonlinear dynamics

Fig. M7.1 A phase portrait of one-dimensional ﬂow along the x-axis.

is based on considering small perturbations. In Figure M7.1 all small disturbances

to P

will decay. Large disturbances that send the phase point x to the right of P

will not decay but will be repelled out to +∞. Thus, we say that the ﬁxed point P

is locally stable only. The concept of global stability will be discussed later.

It should be noted that f does not explicitly depend on time. In this case one

speaks of an autonomous system.Iff depends explicitly on t then the equation is

nonautonomous and usually much more difﬁcult to handle.

Now we practice this way of geometric thinking with a simple example: Find

the ﬁxed points for ˙x = x

− 4 and classify their stability. Solution: In this case

f (x) = x

− 4. Setting f (x

∗

) = 0andsolvingforx

∗

yields x

∗

= 2,x

∗

=−2. To

determine the stability we plot f (x) similarly to Figure M7.1 and obtain a parabola.

Thus, we easily see that x

∗

= 2 is unstable whereas x

∗

=−2isstable.

Now we discuss the concept of linear stability.Letη(t) represent a small per-

turbation away from the ﬁxed point x

∗

η(t) = x(t) − x

∗

(M7.1)

To recognize whether a disturbance grows or decays we need to derive a differential

equation for η(t). Differentiation of η with respect to time results in

˙η = ˙x = f (x) = f (x

∗

+ η)(M7.2)

Now we carry out a Taylor expansion of f (x) and discontinue the series after the

linear term since only small perturbations are admitted:

f (x

∗

+ η) = f (x

∗

) + ηf



∗

) + O(η

)(M7.3)

Suppose that f



∗

) = 0, then the O(η

) terms may be ignored. Since f (x

∗

) = 0

we obtain

˙η = ηf



∗

)(M7.4)

M7.1 One-dimensional ﬂow 113

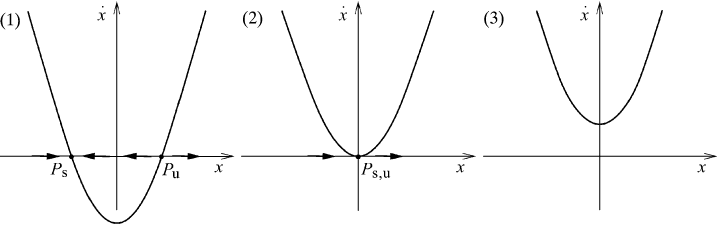
Fig. M7.2 Saddle-node bifurcation. Curve (1): r<0, stable ﬁxed point P

, unstable ﬁxed

point P

. Curve (2): r = 0, half-stable ﬁxed point P

s,u

. Curve (3): r>0, no ﬁxed point.

The linearization about x

∗

shows that η(t) grows exponentially in time if



∗

) > 0 and decays if f



∗

) < 0. If f



∗

) = 0, the O(η

) terms cannot

be neglected and a nonlinear analysis is needed in order to determine the stability.

In the previous example f



∗

= 2) = 4 so that the ﬁxed point x

∗

= 2 is unstable.

Since f



∗

=−2) =−4, the ﬁxed point x

∗

=−2isstable.

Consider now the problem ˙x = x

. The ﬁxed point is x

∗

= 0. In this example

the linear stability analysis fails since f



∗

= 0) = 0. A plot of f (x) = x

shows,

however, that the origin is an unstable ﬁxed point.

M7.1.2 Bifurcation

More instructive than the above examples is the dependence of x on a parameter

since now qualitative changes in the dynamics of systems may occur as the param-

eter is varied. Whenever this change occurs we speak of bifurcation. The parameter

values at which bifurcations occur are called bifurcation points. We will now brieﬂy

discuss various types of bifurcations.

M7.1.2.1 Saddle-node bifurcation

A saddle-node bifurcation is the basic mechanism by which ﬁxed points are created

or destroyed. Consider the equation ˙x = r +x

,wherer is a parameter. Examples

of this type may be found in various textbooks or may be constructed. The result of

the analysis is shown in Figure M7.2. If r<0 we have one stable and one unstable

ﬁxed point (curve 1). As the parameter r approaches 0 from below, the parabola

moves up and the two ﬁxed points move toward each other until they collide into a

half-stable ﬁxed point P

s,u

at x

∗

= 0 (curve 2). The half-stable ﬁxed point vanishes

with r>0 as shown by curve 3.

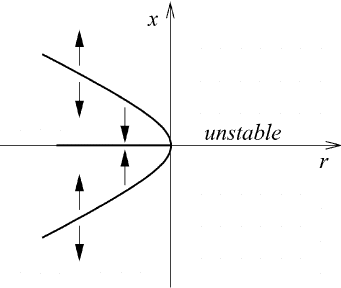
There are other possibilities for depicting bifurcations. A popular way is to select

r as the abscissa and x as the ordinate. Setting ˙x = 0, the curve r =−x

consists

114 Introduction to the concepts of nonlinear dynamics

Fig. M7.3 An alternate bifurcation diagram for the saddle-node bifurcation.

of all ﬁxed points of the system; see Figure M7.3. In agreement with Figure M7.2,

there is no ﬁxed point for r>0. The arrows in Figure M7.3 indicate the direction

of movement toward the ﬁxed-point curve or away from it, thus describing regions

of stability and instability, respectively. The origin itself is called a turning point.

M7.1.2.2 Transcritical bifurcation

There are situations in which a ﬁxed point must exist for all parameter values of

r and cannot be destroyed. However, such a ﬁxed point may change its stability

characteristics as r is varied. The transcritical bifurcation provides the standard

example. The normal form of this type of bifurcation is ˙x = x(r − x). There

exists a ﬁxed point x

∗

= 0 that is independent of r. Various situations are shown

in Figure M7.4. For r<0, x

∗

= r is an unstable ﬁxed point P

whereas x

∗

= 0is

a stable ﬁxed point P

.Asr → 0, the unstable ﬁxed point approaches the origin,

colliding with it when r = 0. Now x

∗

= 0 is a half-stable ﬁxed point P

s,u

. Finally,

for r>0 the origin becomes unstable whereas x

∗

= r is a stable ﬁxed point.

In this case of transcritical bifurcation the two ﬁxed points have not disappeared

after the collision with the origin. In fact, an exchange of stability has taken place

between the two ﬁxed points. This kind of behavior is in contrast to the saddle-node

bifurcation, whereby ﬁxed points are created and destroyed.

M7.1.2.3 Pitchfork bifurcation

This type of bifurcation results from physical problems having symmetry proper-

ties. There are two types of pitchfork bifurcations.

M7.1.2.3.1. Supercritical pitchfork bifurcation The normal form is given by ˙x =

rx −x

. This equation is invariant if the variables x and −x are interchanged. The

plot of this function is shown in Figure M7.5. If r ≤ 0 the origin is the only ﬁxed

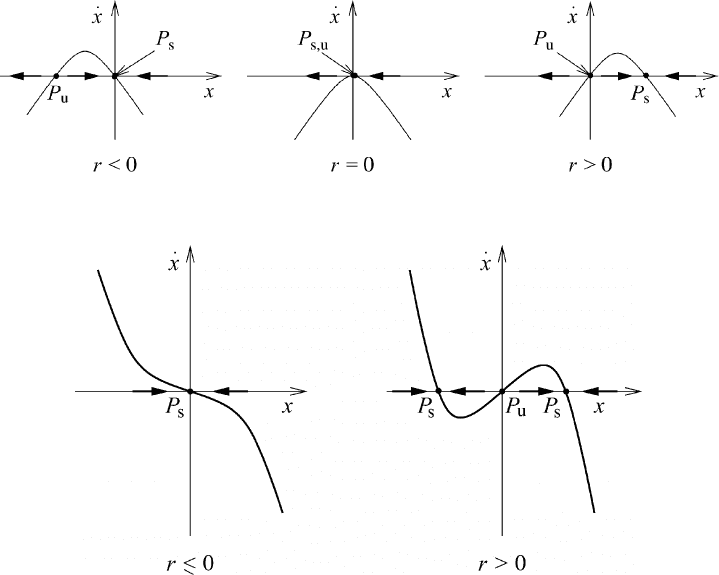
M7.1 One-dimensional ﬂow 115

Fig. M7.4 Transcritical bifurcation.

Fig. M7.5 Supercritical pitchfork bifurcation for ˙x = rx − x

point which is stable. The two curves are quite similar, so only one curve is shown.

The stability decreases as r approaches zero. For r = 0 the origin is still stable but

more weakly so. If r>0 there are three ﬁxed points. The ﬁxed point at the origin

is unstable; the remaining two ﬁxed points are stable.

The curious name pitchfork derives from the bifurcation diagram shown in

Figure M7.6. We set ˙x = 0 and plot x

= r, yielding a parabola for r>0. From

the corresponding curve of Figure M7.5 we recognize that the upper and lower

branches refer to stability. If x = 0butr>0, we ﬁnd instability along the positive

part of the abscissa. For x = 0butr<0, from curve 1 of Figure M7.5 we ﬁnd

stability along the negative part of the abscissa.

M7.1.2.3.2 Subcritical pitchfork bifurcation A simple example is given by ˙x = rx+x

see Figure M7.7. For r ≥ 0 the origin is the only ﬁxed point and it is unstable.

Nonzero ﬁxed points exist only for r<0, which are unstable while now the

origin is stable. The corresponding bifurcation diagram is depicted in Figure M7.8.

Comparison with Figure M7.6 shows that the bifurcation diagrams of the subcritical

and supercritical pitchforks are inverted with respect to each other.

116 Introduction to the concepts of nonlinear dynamics

Fig. M7.6 A bifurcation diagram for ˙x = rx − x

Fig. M7.7 Subcritical pitchfork bifurcation ˙x = rx + x

M7.2 Two-dimensional ﬂow

M7.2.1 Linear stability analysis

Let us consider the two-dimensional linear system

˙x = ax + by

˙y = cx + dy

x = Ax with x =









,A=









(M7.5)

where a, b,c, d are constants. The solutions to (M7.5) can be viewed as trajectories

moving on the (x,y)-phase plane. Much can be learned from a very simple example,

˙x = ax, ˙y =−y (M7.6)

M7.2 Two-dimensional ﬂow 117

Fig. M7.8 A bifurcation diagram for ˙x = rx + x

Here the system is uncoupled so that the solution can be found separately for each

equation:

x(t) = x

exp(at),y(t) = y

exp(−t)(M7.7)

The initial values are (x

). The sign of the constant a determines the type of

ﬂow, which in this case can easily be depicted; see Figure M7.9. For a<0every

point (x

) approaches the origin as t →∞. The direction of approach depends

on the size of a relative to −1. Figure M7.9(a) shows the situation for a<−1. The

ﬁxed point (x

∗

= 0,y

∗

= 0) is known as a stable node.Ifa =−1 the approaches

on the abscissa and the ordinate are equally fast so that all trajectories are straight

lines through the origin as shown in part (b) of the ﬁgure. This also follows from

(M7.7), which in this case may be written as y(t)/x(t) = y

= constant. This

arrangement is called a symmetric node or a star.

When a = 0 a dramatic change in the ﬂow pattern takes place. Now x(t) = x

so that there is an inﬁnite line of ﬁxed points (x

∗

= 0) along the x-axis

(Figure M7.9(c)). These stable ﬁxed points are approached from above and below

by vertical trajectories depending on the sign of y

. Finally, for a>0, we obtain

a situation in which (x

∗

) = (0, 0). This is known as a saddle point. With the

exception of the trajectories on the y-axis all trajectories are heading out for +∞

or −∞ along the x-axis. In forward time, these trajectories are asymptotic to the

x-axis; in backward time (t →−∞) they are asymptotic to the y-axis. The y-axis

is known as the stable manifold of the saddle point. More precisely, this is the set of

initial conditions (x

) such that [x(t),y(t)] → (0, 0) as t →∞. Analogously,

the unstable manifold of the saddle point is the set of initial conditions (x

)such

that [x(t),y(t)] → (0, 0) as t →−∞. In this example the unstable manifold is

the x-axis. It is seen that a typical trajectory approaches the unstable manifold for

t →∞and the stable manifold for t →−∞.

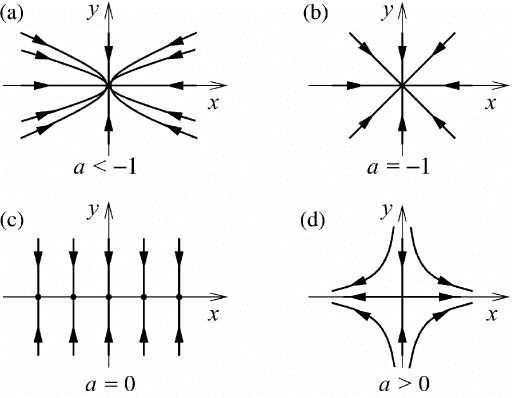
118 Introduction to the concepts of nonlinear dynamics

Fig. M7.9 Flow patterns of the differential-equation system (M7.7) for various values of

the parameter a.

At this point it is opportune to introduce some important terminologies. Referring

to Figures M7.9(a) and (b), (x

∗

) = (0, 0) is classiﬁed as an attracting ﬁxed point

since all trajectories starting near this point approach the origin, i.e. [x(t),y(t)] →

(0, 0) as t →∞. If all path directions are reversed this point is known as a repellor.

If all trajectories that start sufﬁciently close to (0, 0) remain close to it for all time,

not just as t →∞, then the ﬁxed point is called Liapunov stable. In parts (a),

(b), and (c) of Figure M7.9 the origin is Liapunov stable. From Figure M7.9(c) it

can be seen that a ﬁxed point can be Liapunov stable but not attracting. Here the

ﬁxed point is called neutrally stable. In Figure M7.9(d) the ﬁxed point is neither

attracting nor Liapunov stable, so (x

∗

) = (0, 0) is unstable.

M7.2.2 Classiﬁcation of linear systems

We will now consider the general solution to the linear system by seeking trajecto-

ries of the form

x(t) = exp(λt) b (M7.8)

where the time-independent vector b = 0 must be determined. Substitution of

(M7.8) into (M7.5) yields

Ab = λb or (A − Eλ)b = 0(M7.9)

Here matrix notation has been utilized and E is the identity matrix. As usual, the

eigenvalues λ

1,2

can be found by solving the equation for the determinant of the

M7.2 Two-dimensional ﬂow 119

matrix (A − λE):



a − λb

cd− λ



= 0 =⇒ λ

1,2



τ ±



− 4



(M7.10)

where τ = a +d is the trace and  = ad −bc is the determinant of A. The solution

to (M7.5) may now be written as

x(t) = C

exp(λ

t) b

+ C

exp(λ

t) b

(M7.11)

In general, the constants C

and the eigenvectors b

, b

of the eigenvalues λ

,λ

are complex quantities.

As an example, let us consider the phase-plane analysis of the simple harmonic

oscillator

m¨x + kx = 0(M7.12)

where m is the mass and k is Hooke’s constant. By setting ˙x = y, this second-

order differential equation may be written as a system of two ﬁrst-order differential

equations:

˙x = y, ˙y =−ω

x with ω

= k/m (M7.13)

From this system we immediately recognize that the ﬁxed point is located at

∗

) = (0, 0). On dividing ˙y by ˙x, we ﬁnd the equation of the trajectory which

upon integration gives the equation of an ellipse:

=−ω

=⇒ y

+ ω

= C (M7.14)

The situation is depicted in Figure M7.10. The trajectories form closed lines around

the origin, which is therefore known as a center. The direction of ﬂow around

the center is best recognized by placing an imaginary particle or phase point at a

convenient point such as (x = 0,y > 0). Thus, from (M7.13) it follows that ˙x>0,

so the ﬂow is clockwise. Finally, with the help of (M7.5), the eigenvalues of the

system may be easily found as λ

1,2

=±iω, showing that a center is characterized

by purely imaginary eigenvalues.

Fig. M7.10 The center for the simple harmonic oscillator.

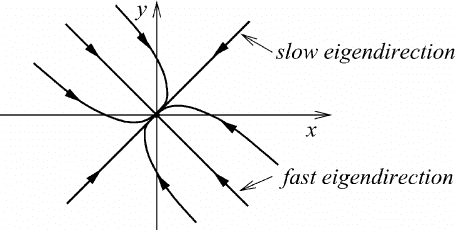
120 Introduction to the concepts of nonlinear dynamics

Fig. M7.11 A phase portrait of slow and fast eigendirections.

Before we summarize all important results, let us consider two more simple but

important examples. Suppose that, for a given problem, the two eigenvalues are

negative, say λ

<λ

< 0. Thus, both eigensolutions decrease exponentially so

that the ﬁxed point is a stable node. The eigenvector resulting from the smaller

eigenvalue

is known as the slow eigendirection, while the eigenvector due to

the larger value

is called the fast eigendirection. Trajectories typically approach

the origin tangentially to the slow eigendirection for t →∞. In backward time,

t →−∞, the trajectories become parallel to the fast eigendirection. The phase

portrait may have the appearance of Figure M7.11 representing a stable node.

Reversing the directions of the trajectories results in a typical portrait of an unstable

node.

Let us brieﬂy return to the phase portrait of the harmonic oscillator; see

Figure M7.10. Since nearby trajectories are neither attracted to nor repelled from

the ﬁxed point, the center is classiﬁed as neutrally stable. If the harmonic oscillator

were slightly damped, the equation of motion (M7.12) would be modiﬁed to read

m¨x + dm ˙x + kx = 0(M7.15)

where d>0 is the damping constant. Now the trajectories cannot close because the

oscillator loses some energy during each cycle. Weak damping is characterized by

− 4<0. The resulting phase portrait is a stable spiral.Sinceτ =−d<0the

eigenvalues are complex conjugates with a negative real part τ/2 =−d/2. Owing

to Euler’s formula the solution contains the term exp(−τt/2) yielding exponentially

decaying oscillations. Thus the ﬁxed point is a stable spiral. If d<0 in (M7.15),

the ﬁxed point is an unstable spiral; see Figure M7.12.

It may happen that the eigenvalues of the matrix A are degenerate, i.e. λ

= λ

.In

this case there exist two possibilities: Either there are two independent eigenvectors

spanning the two-dimensional phase plane or only one eigenvector exists, so that

the eigenspace is one-dimensional, and the ﬁxed point is a degenerate node.