Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

M5.2 Time differentiation of vectors and dyadics 81
The covariant spatial operators appearing in this equation have previously been
defined by using the ordinary spatial derivatives so that (M5.32) can be evaluated
entirely in terms of ordinary derivatives. Scalar multiplication of both sides by
q
i
results in the definition of the covariant time differentiation of the covariant
measure number A
i
:
∂A
i
∂t
=
∂A
i
∂t
− A
n
∇
i
(W
n
+ W
n
D
)
(M5.33)
By precisely the same procedure we find
∂A
i
∂t
=
∂A
i
∂t
+ A
n
∇
n
(W
i
+ W
i
D
)
(M5.34)
giving the equation for the covariant time differentiation of the contravariant mea-
sure number A
i
.
Of particular importance is the covariant time differentiation of the metric fun-
damental quantities g
ij
and g
ij
. The starting point of the analysis, as might be
expected by now, is the time-invariant unit dyadic E. The mathematical operation
is given by
∂
E
∂t
= 0 =⇒
∂
∂t
(q
n
q
n
) =
∂
∂t
(g
nr
q
r
q
n
) = q
r
q
n
∂g
nr
∂t
= 0(M5.35)
showing that the metric fundamental quantity g
ij
is a constant in covariant time
differentiation. Proceeding analogously we find the same result for g
ij
so that
∂g
ij
∂t
= 0,
∂
g
ij
∂t
= 0
(M5.36)
From these expressions follow the important relations
∂A
i
∂t
=
∂
∂t
(g
in
A
n
) = g
in
∂A
n
∂t
∂
A
i
∂t
=
∂
∂t
(g
in
A
n
) = g
in
∂A
n
∂t
(M5.37)
By now it should be apparent that operations with covariant derivatives are easy and
very convenient. Otherwise, the many differential relations involving basis vectors
would be very tedious to apply.
Now we need to introduce an expression for the individual covariant differential
time operator. This expression is very simply obtained since we have already
82 The method of covariant differentiation
provided the necessary ingredients. In analogy to the definition of the individual
time derivative
d
dt
=
∂
∂t
+ ˙q
n
∂
∂q
n
=
∂
∂t
+ v
n
∂
∂q
n
=
∂
∂t
+ v
n
∇
n
(M5.38)
we may define the individual covariant time derivative by
d
dt
=
∂
∂t
+ v
n
∇
n
(M5.39)
Using (M5.6) and (M5.33) we immediately obtain
d
A
k
dt
=
∂
A
k
∂t
+ v
n
∇
n
A
k
=
∂A
k
∂t
− A
n
∇
k
(W
n
+ W
n
D
) + v
n
∇
n
A
k
− A
m
m
nk
(M5.40)
which is the desired expression. Finally, replacing the covariant spatial derivative,
using (M5.4), gives
dA
k
dt
=
∂A
k
∂t
− A
n
∇
k
(W
n
+ W
n
D
) + (W
m
+ W
m
D
)
n
mk
+ v
n
∇
n
A
k
− A
m
m
nk
(M5.41)
The involvement of the measure numbers of v
P
should not be surprising in view of
(M5.33). Similarly, the application of (M5.39) to the contravariant measure number
A
k
leads to
dA
k
dt
=
∂A
k
∂t
+ A
n
∇
n
(W
k
+ W
k
D
) + (W
m
+ W
m
D
)
k
nm
+ v
n
∇
n
A
k
+ A
m
k
nm
(M5.42)
M5.3 The local dyadic of v
P
The representation of the motion in general coordinate systems requires a suitable
description of the local dyadic of v
P
= v
+ v
D
. First, we split the local dyadic
of v
P
into its symmetric and antisymmetric parts. Utilizing the conjugated dyadic
∇v
P
of ∇v
P
, we may write according to (M2.27)
∇v
P
=
1
2
(∇v
P
+
∇v
P
) +
1
2
(∇v
P
−
∇v
P
) = D
P
+
P
(M5.43)
M5.4 Problems 83
The symmetric part D
P
of (M5.43) is given by
D
P
=
1
2
(∇v
+
∇v
) +
1
2
(∇v
D
+
∇v
D
) =
1
2
(∇v
D
+
∇v
D
)
=
1
2
q
m
∇
m
(W
n
D
q
n
) +
1
2
q
n
∇
n
(W
m
D
q
m
) =
1
2
(q
m
q
n
∇
m
W
n
D
+
q
n
q
m
∇
n
W
m
D
)
=
1
2
(q
m
q
n
∇
m
W
n
D
+ q
m
q
n
∇
n
W
m
D
) =
1
2
q
m
q
n
(∇
m
W
n
D
+∇
n
W
m
D
) = d
mn
q
m
q
n
(M5.44)
The term ∇v
+
∇v
vanishes because ∇v
is an antisymmetric tensor. The
measure number d
ij
is best obtained from (M5.44) by scalar multiplication first by
q
i
andthenbyq
j
.Theresultis
d
ij
=
1
2
(∇
i
W
j
D
+∇
j
W
i
D
)(M5.45)
Using scalar multiplication to obtain d
ij
insures against errors, while by comparison
the suffices i and j might easily be misplaced.
The antisymmetric dyadic
P
is given by
P
=
1
2
(∇v
−
∇v
) +
1
2
(∇v
D
−
∇v
D
) = ω
mn
q
m
q
n
(M5.46)
Analogously to d
ij
we find the measure numbers ω
ij
:
ω
ij
=
1
2
(∇
i
W
j
−∇
j
W
i
) +
1
2
(∇
i
W
j
D
−∇
j
W
i
D
)
=
1
2
(∇
i
W
j
−∇
j
W
i
) +
1
2
(∇
i
W
j
D
−∇
j
W
i
D
) = ω
ij
+ ω
ij
D
(M5.47)
The covariant derivatives in (M5.47) have been replaced with the help of (M5.6).
The abbreviations ω
ij
and ω
ij
D
, which have been introduced in (M5.47), are given
by
ω
ij
=
1
2
(∇
i
W
j
−∇
j
W
i
) =
1
2
(∇
i
W
j
−∇
j
W
i
)
ω
ij
D
=
1
2
(∇
i
W
j
D
−∇
j
W
i
D
) =
1
2
(∇
i
W
j
D
−∇
j
W
i
D
)
(M5.48)
Furthermore, from (M5.47) we obtain the useful relations
∇
i
W
j
= 2ω
ij
+∇
j
W
i
or ∇
i
W
j
= 2ω
ij
+∇
j
W
i
∇
i
W
j
D
= 2ω
ij
D
+∇
j
W
i
D
or ∇
i
W
j
D
= 2ω
ij
D
+∇
j
W
i
D
(M5.49)
M5.4 Problems
M5.1: In (M5.14) only the first expression has been derived. Verify the remaining
expressions.

M6
Integral operations
M6.1 Curves, surfaces, and volumes in the general q
i
system
An arbitrary curve in space may be viewed as a coordinate line q
1
of a curvilinear
coordinate system. Therefore, the differential increment dr along this curve can be
written in the form
dr = dq
1
q
1
= dq
1
√
g
11
e
1
= dq
*
1
e
1
= dr e
1
(M6.1)
where the basis vector q
1
is tangential to the coordinate line q
1
at a given point P
as shown in Figure M6.1. Instead of using the arbitrary basis vector q
1
,wemay
also employ the unit vector e
1
which is identical to the unit tangent vector at P .
This leads to the introduction of the physical measure number dq
*
1
of the vector dr
which is equivalent to the differential arclength dr.
Now we wish to discuss very briefly the geometrical meaning of a coordinate line.
For simplicity let us first consider the Cartesian coordinate system. It is immediately
apparent that the intersection of the surfaces y = constant and z = constant
produces a straight line that may be chosen as the x-axis. The y-andz-axes
are found by intersecting the surfaces x = constant,z= constant and x =
constant,y= constant, respectively. Analogously, in the curvilinear coordinate
system the intersection of two surfaces q
i
= constant,q
j
= constant yields the
coordinate line of the corresponding third coordinate q
k
.
An arbitrary surface in three-dimensional space may be defined by two coor-
dinate lines q
1
and q
2
with q
3
= constant; see Figure M6.2. Since q
1
and q
2
are
tangent vectors to the coordinate lines q
1
and q
2
, they span a tangential plane to
the surface q
3
= constant. The vector q
3
is a tangent vector to the q
3
-coordinate
line and e
3
= q
3
/
√
g
33
is the corresponding unit vector. In our investigation we
set the unit vector e
3
equal to the unit normal e
N
of the surface q
3
= constant.
Hence, we are dealing with a semi-orthogonal coordinate system. In this system
e
3
is perpendicular to the basis vectors q
1
and q
2
so that e
3
is also parallel to the
84

M6.1 Curves, surfaces, and volumes in the general q
i
system 85
-coordinate line
1
Fig. M6.1 The q
1
-coordinate line in space, corresponding basis vector q
1
, and position
vector dr.
Fig. M6.2 The coordinate surface q
3
= constant in three-dimensional space. The coor-
dinate lines drawn on the surface are q
1
and q
2
. The corresponding basis vectors are q
1
and q
2
, respectively. The unit vector of the q
3
-coordinate line e
3
is the normal vector to
the surface.
direction defined by the cross product q
1
×q
2
. In summary, we may write the unit
normal vector e
3
in the following forms:
e
3
=
q
3
√
g
33
=
q
3
|
q
3
|
=
q
1
× q
2
|
q
1
× q
2
|
=
q
3
√
g
q
3
√
g
=
q
3
|
q
3
|
=
q
3
g
33
= e
3
(M6.2)
where we have used the properties of the reciprocal systems (M1.55). Hence,
in the semi-orthogonal system we have e
3
= e
3
and g
33
g
33
= 1. It should not
be concluded, however, that g
ii
g
ii
= 1,i= 1, 2, since we are dealing with
a semi-orthogonal coordinate system only, so that the general formula (M1.88)
for orthogonal systems does not apply. Moreover, from the general expressions
(M1.37) and (M1.57) of the scalar triple product we obtain for the semi-orthogonal
system
[q
1
, q
2
, q
3
][q
1
, q
2
, q
3
] =
q
1
, q
2
,
q
3
√
g
33
q
1
, q
2
,
q
3
g
33
= [q
1
, q
2
, e
3
][q
1
, q
2
, e
3
] = 1
(M6.3)
We will now consider a directed surface area element dS that is spanned by the
two vectors q
1
dq
1
and q
2
dq
2
having the direction q
1
× q
2
. Utilizing (M6.2) we

86 Integral operations
may write
dS = q
1
× q
2
dq
1
dq
2
= q
3
√
gdq
1
dq
2
= e
3
g
33
√
gdq
1
dq
2
=
|
dS
|
e
3
with
|
dS
|
=
g
33
√
gdq
1
dq
2
=
q
1
, q
2
,
q
3
√
g
33
dq
1
dq
2
= [q
1
, q
2
, e
3
] dq
1
dq
2
(M6.4)
Of some importance is the metric fundamental form for the given surface q
3
=
constant. Since an arbitrary line element on this surface is defined by dr = q
1
dq
1
+
q
2
dq
2
, the metric fundamental form in the two-dimensional case is given by
dr · dr = (q
1
dq
1
+ q
2
dq
2
) · (q
1
dq
1
+ q
2
dq
2
)
= g
11
(dq
1
)
2
+ 2g
12
dq
1
dq
2
+ g
22
(dq
2
)
2
(M6.5)
If the coordinate lines on the surface are orthogonal, the quantity g
12
vanishes.
In general, the metric fundamental form is given by
dr · dr = g
mn
dq
m
dq
n
with dr = q
n
dq
n
(M6.6)
In the Cartesian system this form reduces to
dr · dr = dx
m
dx
m
(M6.7)
At this point it is opportune to present a few remarks on the Riemannian space
and the Euclidian space. In order not to disrupt our train of thought, we present
some basic ideas to the interested reader in the appendix to this chapter. On the
surface q
3
= constant the two-dimensional Hamilton operator may be written as
∇
2
= q
1
∂
∂q
1
+ q
2
∂
∂q
2
(M6.8)
The contravariant and the covariant basis vectors are related in the following forms:
q
1
=
q
2
× e
3
[q
1
, q
2
, e
3
]
, q
2
=
e
3
× q
1
[q
1
, q
2
, e
3
]
q
1
=
q
2
× e
3
[q
1
, q
2
, e
3
]
, q
2
=
e
3
× q
1
[q
1
, q
2
, e
3
]
(M6.9)
with e
3
= e
3
. Finally, the relationship between the three- and the two-dimensional
Hamilton operators is given by
∇=∇
2
+ q
3
∂
∂q
3
(M6.10)
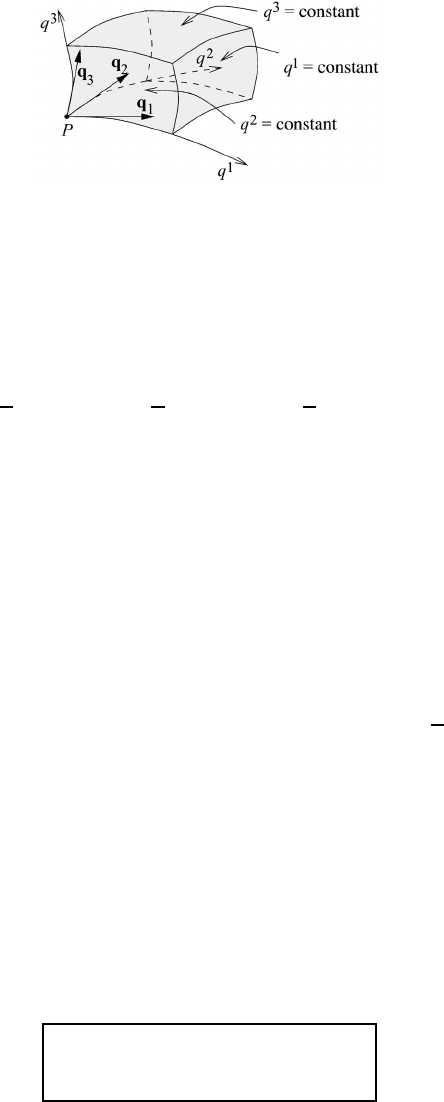
M6.2 Line integrals, surface integrals, and volume integrals 87
Fig. M6.3 A volume element dτ in the general curvilinear nonorthogonal coordinate
system defined by the three coordinate surfaces q
i
= constant.
Now we consider an arbitrary surface area element dS in the q
i
-space, which
may be decomposed as
dS = q
2
× q
3
dq
2
dq
3
+ q
3
× q
1
dq
3
dq
1
+ q
1
× q
2
dq
1
dq
2
= q
1
√
gdq
2
dq
3
+ q
2
√
gdq
3
dq
1
+ q
3
√
gdq
1
dq
2
= q
1
dS
1
+ q
2
dS
2
+ q
3
dS
3
= (dS)
1
+ (dS)
2
+ (dS)
3
(M6.11)
Reference to (M6.4) shows that this expression is a special case of (M6.11). Clearly,
the surface area elements q
i
dS
i
are projections of dS in the directions q
i
parallel
to the planes spanned by (q
j
× q
k
).
In order to define a volume element in the generalized q
i
-coordinate system we
draw three coordinate surfaces as shown in Figure M6.3. The intersection of these
surfaces results in the three coordinate lines. The differential volume element dτ
is now given by
dτ = [q
1
dq
1
, q
2
dq
2
, q
3
dq
3
] = q
1
dq
1
· (q
2
dq
2
× q
3
dq
3
) =
√
gdq
1
dq
2
dq
3
(M6.12)
M6.2 Line integrals, surface integrals, and volume integrals
As before we consider a curve k in space, which is formed by the coordinate line
q
1
. Along this curve a field vector A may be written as A(q
1
) while a vectorial line
element dr is given by (M6.1). The line integral of A along the curve k between
the points (q
1
)
1
and (q
1
)
2
is defined by
L =
(q
1
)
2
(q
1
)
1
drA=
(q
1
)
2
(q
1
)
1
dq
1
(q
1
A)
(M6.13)
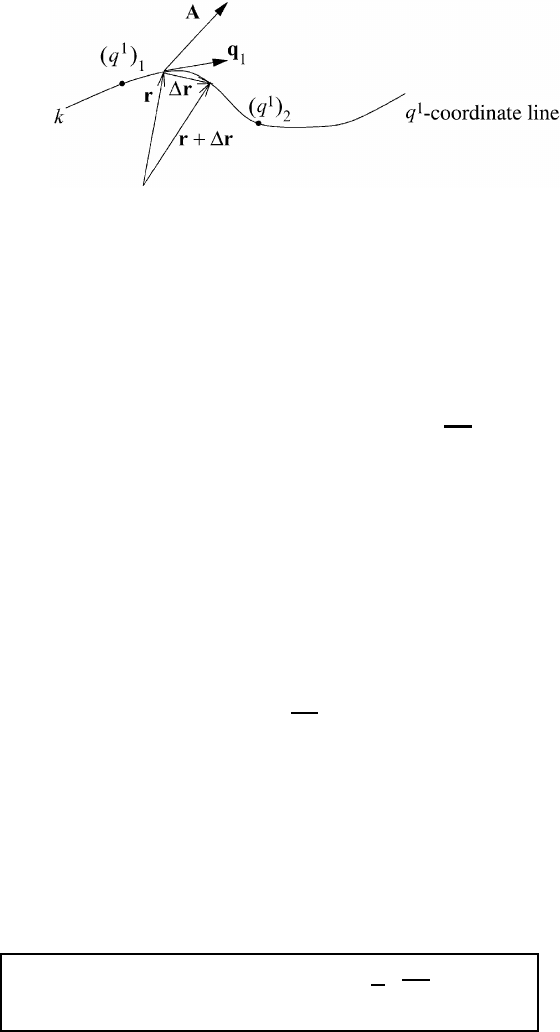
88 Integral operations
Fig. M6.4 An illustration of the curve k in space, showing the parameters used in the
definition of the line integral (M6.13).
This situation is illustrated in Figure M6.4. In general A is a three-dimensional
field vector and the line integral a dyadic.
The line integral over the tangential component A
T
= A
1
of A along k is given
by the first scalar of the dyadic
L:
L
I
=
(q
1
)
2
(q
1
)
1
dr · A =
(q
1
)
2
(q
1
)
1
dq
1
(q
1
· A) =
(q
1
)
2
(q
1
)
1
dq
1
(
√
g
11
e
1
·A) =
(q
1
)
2
(q
1
)
1
dr A
1
(M6.14)
This integral is known as the flow integral whenever the field vector A represents
the velocity vector v of the flow field along the curve k.Ifthecurvek is closed
then we speak of the circulation integral. This important concept will be discussed
in some detail later.
If it is required to compute the normal component of the vector A along k then
we have to take the vector of
L, which is easily obtained from (M6.13) as
L
×
=
(q
1
)
2
(q
1
)
1
dr × A =
(q
1
)
2
(q
1
)
1
dq
1
(
√
g
11
e
1
× A) =
(q
1
)
2
(q
1
)
1
dr (e
1
× A) (M6.15)
Let us reconsider a surface in space such as the surface q
3
= constant. The vec-
torial surface element (dS)
3
was defined previously by equation (M6.4). According
to (M6.11) we have added the number 3 to indicate the direction of the surface
normal vector. On this surface we draw the coordinate lines q
1
and q
2
as depicted
in Figure M6.5. We assume that a field vector A(q
1
,q
2
) is defined at every point
on the surface. The surface integral which is a dyadic is defined by
S =
S
(dS)
3
A =
(q
1
)
2
(q
1
)
1
dq
1
(q
2
)
2
(q
2
)
1
dq
2
√
g
g
33
e
3
A(q
1
,q
2
)
(M6.16)
While (q
1
)
1
and (q
1
)
2
are fixed boundary coordinates, the boundary coordinates
(q
2
)
1
and (q
2
)
2
of the second integral are functions of q
1
; see Figure M6.5.
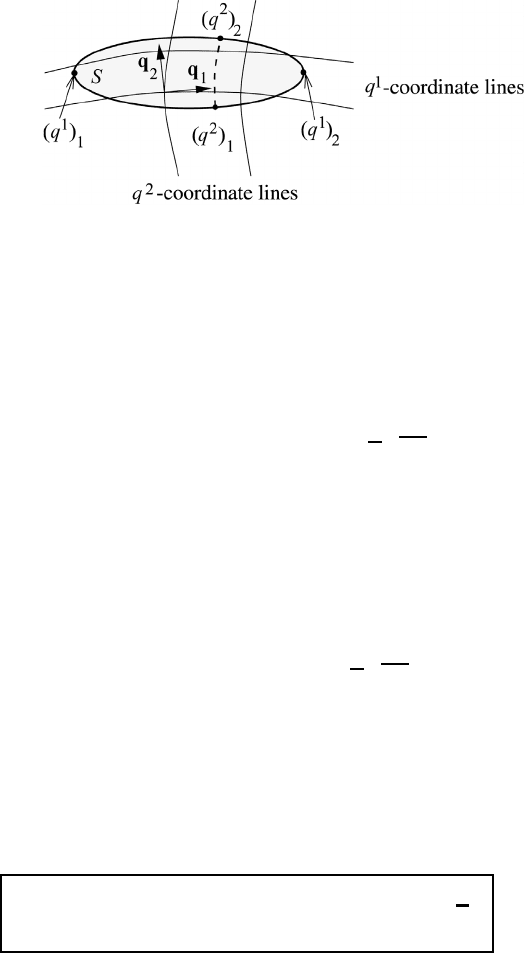
M6.2 Line integrals, surface integrals, and volume integrals 89
Fig. M6.5 An illustration of a surface S in space, showing the basic parameters needed
to define the surface integral (M6.16).
The surface integral over the normal component of A is found by taking the first
scalar of the dyadic S:
S
I
=
(q
1
)
2
(q
1
)
1
dq
1
(q
2
)
2
(q
2
)
1
dq
2
√
g
g
33
A
3
(M6.17)
where A
3
= e
3
·A is the normal component of the vector A with respect to the
surface element. The integral over the tangential component of A is found by taking
the vector of the dyadic S
S
×
=
(q
1
)
2
(q
1
)
1
dq
1
(q
2
)
2
(q
2
)
1
dq
2
√
g
g
33
e
3
× A (M6.18)
Let us consider a surface in space that is enclosing the volume V . By assuming
that the field vector A is known everywhere within the entire domain of integration,
with the help of (M6.12) we obtain the volume integral as
V =
V
dτ A =
(q
1
)
2
(q
1
)
1
dq
1
(q
2
)
2
(q
2
)
1
dq
2
(q
3
)
2
(q
3
)
1
dq
3
√
gA
(M6.19)
As before, the boundary coordinates (q
1
)
1
, (q
1
)
2
are fixed. The boundary coordi-
nates (q
3
)
1
, (q
3
)
2
must be given functions of q
1
and q
2
and the boundary coordinates
(q
2
)
1
, (q
2
)
2
must be given functions of q
1
. The integration proceeds analogously to
the volume integration in the Cartesian coordinate system.

90 Integral operations
Fig. M6.6 Explanation of the terms occurring in equation (M6.20). dS is a directed
surface element on the spatial surface S which is bordered by the line ; dr is a line
element on .
M6.3 Integral theorems
M6.3.1 Stokes’ integral theorem
The Stokes integral theorem relating a surface and a line integral is based on the
following general expression:
S
dS ×∇(···) =
dr(···)
(M6.20)
where the term (···) indicates that this formula may be applied to tensors of arbitrary
rank, that is scalars, vectors, dyadics etc. The derivation of this important equation
will be omitted here since it is given in many mathematical textbooks on vector
analysis. Figure M6.6 depicts the parameters occurring in (M6.20). If the surface
S is closed then the border line vanishes and the right hand side of (M6.20) is zero.
Of great importance are the first scalar and the vector of (M6.20). The first scalar
results in the Stokes integral theorem
S
dS ×∇·A =
S
∇×A · dS =
dr · A =
A
T
dr
(M6.21)
where A
T
is the tangential component of A along the border line . (M6.21) is a
fundamental formula not only in fluid dynamics but also in many other branches
of science. Using Grassmann’s rule (M1.44), we find for the vector of the dyadic
S
(dS ×∇) × A =
S
[∇A − (∇·A)E] ·dS =
dr × A
(M6.22)
where we have used the property of the conjugate dyadics.
