Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

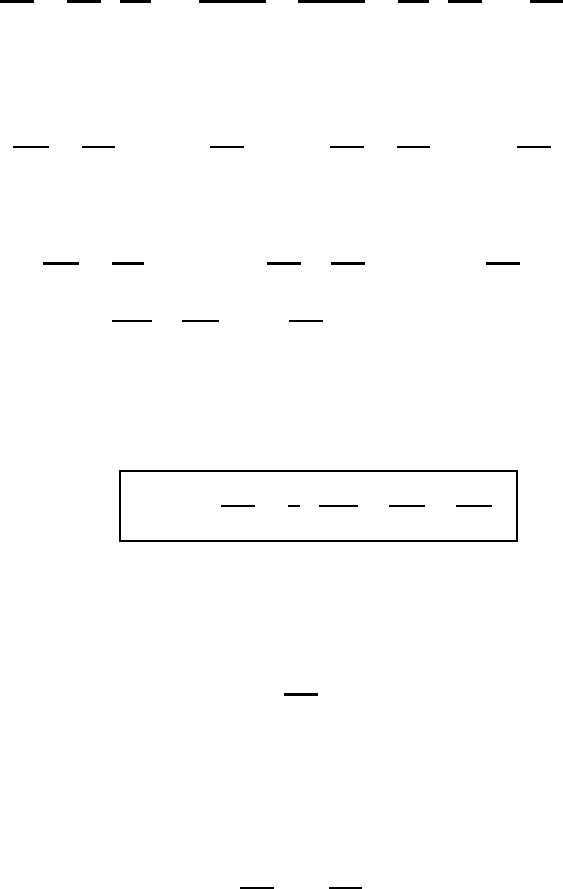
M3.3 The spatial derivative of the basis vectors 51

M3.3 The spatial derivative of the basis vectors

To begin with, we perform the partial differentiation of the covariant basis

vector q

with respect to the contravariant measure number q

. Since the order

of the differentiation may be interchanged, see (M3.18), we obtain the important

identity

∂q

∂

∂q



∂r

∂q



∂

∂q

∂

∂q

∂

∂q



∂r

∂q



∂q

(M3.37)

Differentiation of the covariant metric fundamental quantity g

, using (M3.37),

yields

∂g

∂q

∂

∂q

·q

) =

∂q

·q

+ q

∂q

·q

+ q

∂q

(M3.38)

By obvious steps this equation can be rewritten in the form

∂g

∂q

∂

∂q

·q

) − q

∂q

∂

∂q

·q

) − q

∂q

∂g

∂q

∂g

∂q

− 2q

∂q

(M3.39)

In order to obtain compact and concise differentiation formulas we will introduce

the so-called Christoffel symbols. The Christoffel symbol of the ﬁrst kind is denoted

by 

ij k

and is deﬁned by



ij k

= q

∂q



∂g

∂q

∂g

∂q

−

∂g

∂q



(M3.40)

From this expression it is easily seen that the indices i and j of the Christoffel

symbol may be interchanged, that is 

ij k

= 

jik

Next we perform a dyadic multiplication of (M3.40) with the contravariant basis

vector q

, yielding

∂q

= 

ij k

(M3.41)

It is now possible to introduce the unit dyadic by a very useful mathematical

manipulation called contraction. First we set the covariant index k equal to the

contravariant index l andthenwesumoverk. However, according to the Einstein

summation convention, we introduce the summation index n by setting k = l = n

and obtain

∂q

= E·

∂q

= 

ij n

(M3.42)

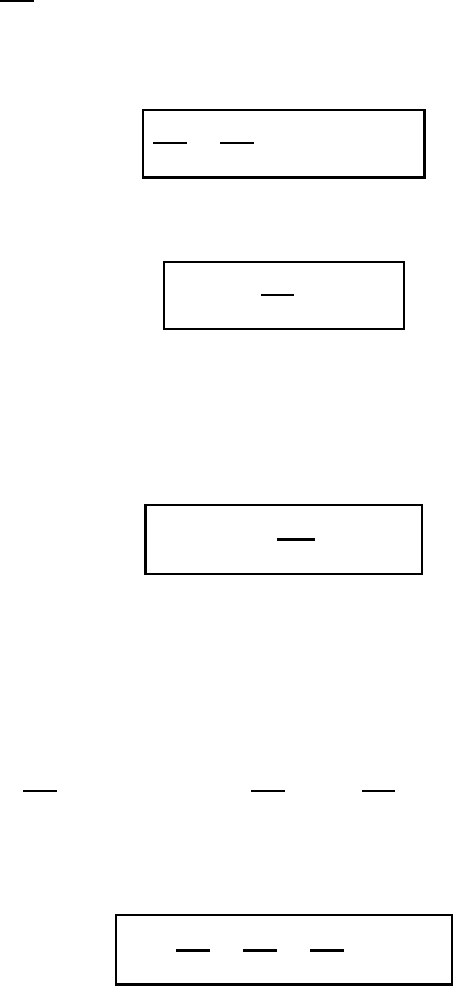
52 Differential relations

Often it is convenient to use the Christoffel symbol of the second kind, 

.This

symbol is obtained from the Christoffel symbol of the ﬁrst kind by lowering the

index of the contravariant basis vectors. Observing (M2.103), we ﬁnd

∂q

= 

ij n

= 

ij n

= 

=⇒ 

= 

ij n

(M3.43)

From (M3.42) and (M3.43) we obtain the desired expression for the spatial deriva-

tive of the covariant basis vector q

∂q

= 

ij n

= 

(M3.44)

With the help of this equation, the gradient of the covariant basis vector q

can be

written in the following concise form:

∇q

= q

∂q

= q



(M3.45)

At ﬁrst glance, the Christoffel symbols have the appearance of tensors. However,

they are not tensors since they do not transform according to the tensor transfor-

mation laws which will be discussed later.

Using equations (M3.36) and (M3.45), the gradient of the vector A, expressed

with the help of the contravariant measure numbers A

, can now be written in the

form

∇A = q



∂A

∂q

+ A





(M3.46)

which required the renaming of the indices in order to extract the dyadic factor

If we wish to express the gradient of the vector A with the help of covariant

measure numbers A

, we must proceed similarly. Differentiation of the scalar

product of the reciprocal basis vectors with respect to q

yields, together with

(M3.44),

∂

∂q

·q

) = 0 =⇒ q

∂q

=−q

∂q

=−

(M3.47)

Dyadic multiplication of the latter equation by the contravariant basis vector q

and

contraction of the mixed tensor (setting k = l and summing, i.e. setting k = l = n)

gives

∂q

=−

(M3.48)

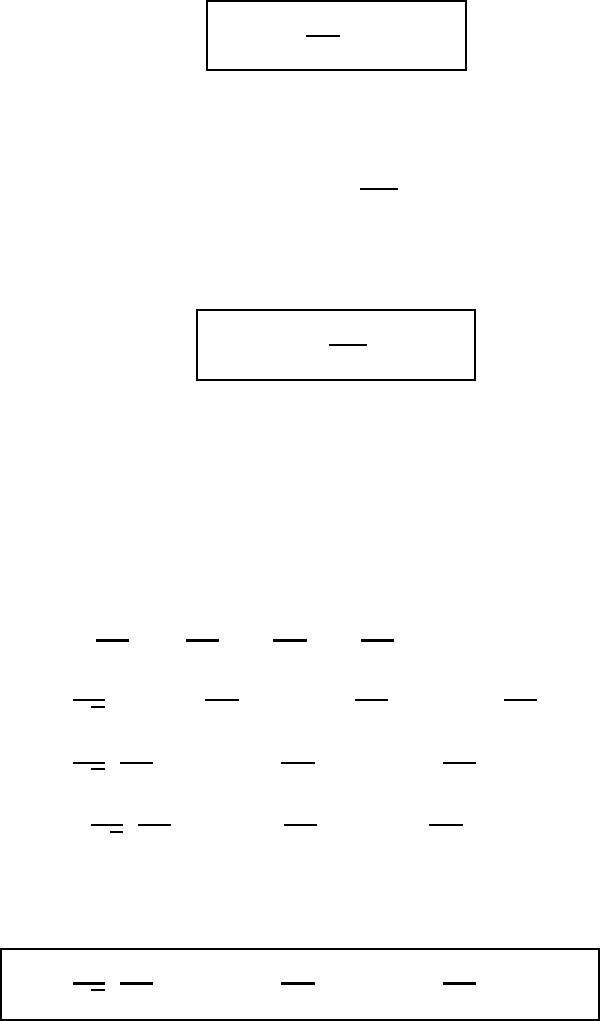
M3.4 Differential invariants in generalized coordinate systems 53

Utilizing this expression, it is a simple matter to ﬁnd the gradient of q

∇q

= q

∂q

=−q



(M3.49)

Finally, we wish to ﬁnd the gradient of the vector A if this vector is expressed in

terms of covariant measure numbers A

. This leads to

∇A =∇(A

) = q

∂A

∂q

− A



(M3.50)

Again, by interchanging the summation indices we can extract the factor q

obtain the more compact form

∇A = q



∂A

∂q

− A





(M3.51)

which should be compared with (M3.46).

M3.4 Differential invariants in generalized coordinate systems

In order to obtain the required invariants, we expand the general form of the local

dyadic ∇A and replace the contravariant basis vectors q

of the gradient operator

by means of formula (M1.55). The result is

∇A = q

∂A

∂q

= q

∂A

∂q

+ q

∂A

∂q

+ q

∂A

∂q

√



× q

)

∂A

∂q

+ (q

× q

)

∂A

∂q

+ (q

× q

)

∂A

∂q



√



∂

∂q

× q

A) +

∂

∂q

× q

A) +

∂

∂q

× q



−

√



∂

∂q

× q

) +

∂

∂q

× q

) +

∂

∂q

× q

)



(M3.52)

It is a little tedious to show that the sum of the three terms within the last set of

large parentheses vanishes. Thus, equation (M3.52) reduces to

∇A =

√



∂

∂q

× q

A) +

∂

∂q

× q

A) +

∂

∂q

× q



(M3.53)

This is the form which will be used to obtain the invariants.

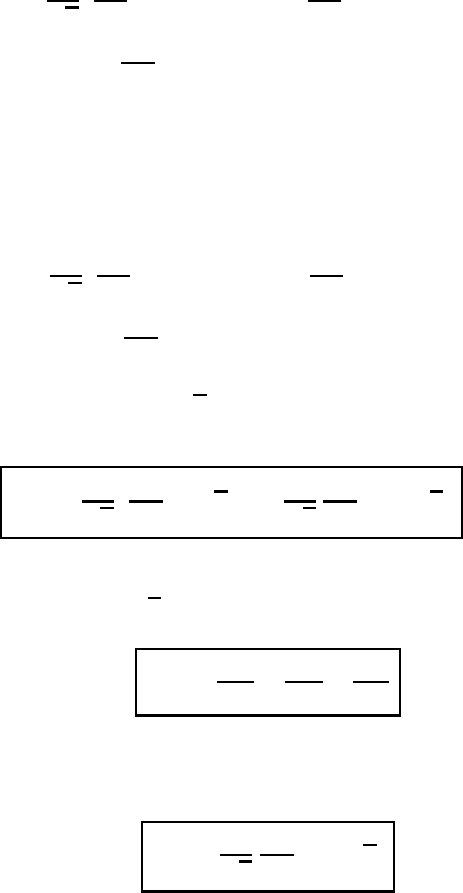
54 Differential relations

M3.4.1 The ﬁrst scalar or the divergence of the local dyadic ∇A

By expressing the vector A with the help of the covariant basis vectors q

and then

taking the scalar product, we ﬁnd

∇·A =

√



∂

∂q

[(q

× q

)·A

] +

∂

∂q

[(q

× q

)·A

]

∂

∂q

[(q

× q

)·A

]



(M3.54)

Let us consider the ﬁrst term in expanded form. Only the term involving q

makes a

contribution; the remaining terms involving q

and q

must vanish since the scalar

triple products are zero. The same arguments hold for the remaining two terms in

(M3.54), so that

∇·A =

√



∂

∂q

[(q

× q

)·A

] +

∂

∂q

[(q

× q

)·A

]

∂

∂q

[(q

× q

)·A

]



(M3.55)

By observing the deﬁnition of

√

g and the rules of the scalar triple product we ﬁnd

the desired relation:

∇·A =

√



∂

∂q

√

g )



√

∂

∂q

·A

√

g )

(M3.56)

with A

= q

·A. In the orthogonal Cartesian system, the divergence expression is

particularly simple since

√

g = 1 so that (M3.56) reduces to

∇·A =

∂A

∂x

∂A

∂y

∂A

∂z

(M3.57)

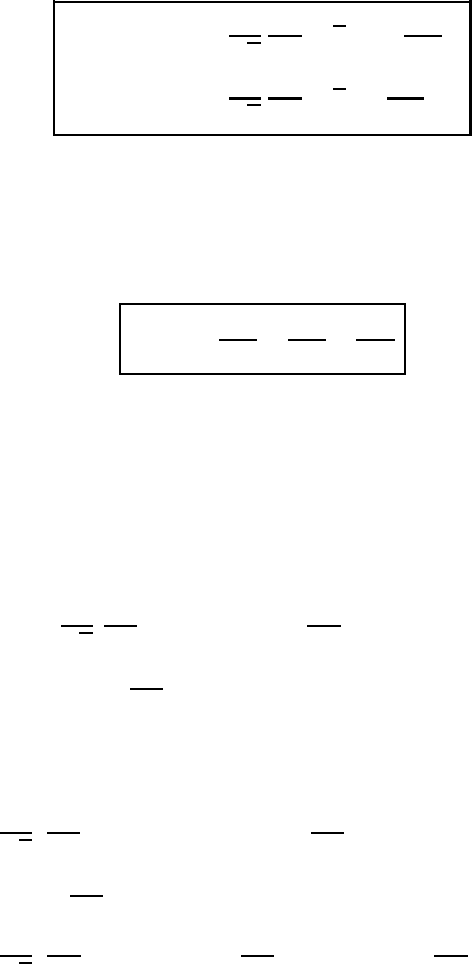
The ﬁrst scalar of the dyadic ∇

B has the same form as (M3.56). In this case,

however, we have to watch the position of the dyadic as stated in

∇·B =

√

∂

∂q

·B

√

g )

(M3.58)

The reader is invited to verify this formula. This is an easy but somewhat tedious

task since it involves the spatial differentiation of the basis vectors.

M3.4 Differential invariants in generalized coordinate systems 55

M3.4.2 The Laplacian of a scalar ﬁeld function

Deﬁning the vector A =∇ψ, we ﬁnd with the help of (M3.56) the desired

expression

∇·∇ψ =∇

ψ =

√

∂

∂q



√

·q

∂ψ

∂q



√

∂

∂q



√

∂ψ

∂q



(M3.59)

where ∇

is the so-called Laplace operator. Some authors denote the Laplacian

operator by the symbol . We shall reserve the symbol  for representing the

difference operator. Only in the Cartesian system does (M3.59) reduce to the

following very simple form:

∇·∇ψ =

∂

∂x

∂

∂y

∂

∂z

(M3.60)

M3.4.3 The vector of the local dyadic ∇A

Taking the cross product of the gradient operator with the vector A in equation

(M3.53), we ﬁrst obtain three vectorial triple cross products:

∇×A =

√



∂

∂q

[(q

× q

) × A] +

∂

∂q

[(q

× q

) × A]

∂

∂q

[(q

× q

) × A]



(M3.61)

Application of the Grassmann rule (M1.44) immediately results in

∇×A =

√



∂

∂q

[(A·q

− (A·q

] +

∂

∂q

[(A·q

− (A·q

]

∂

∂q

[(A·q

− (A·q

]



√



∂

∂q

− A

) +

∂

∂q

− A

) +

∂

∂q

− A

)



(M3.62)

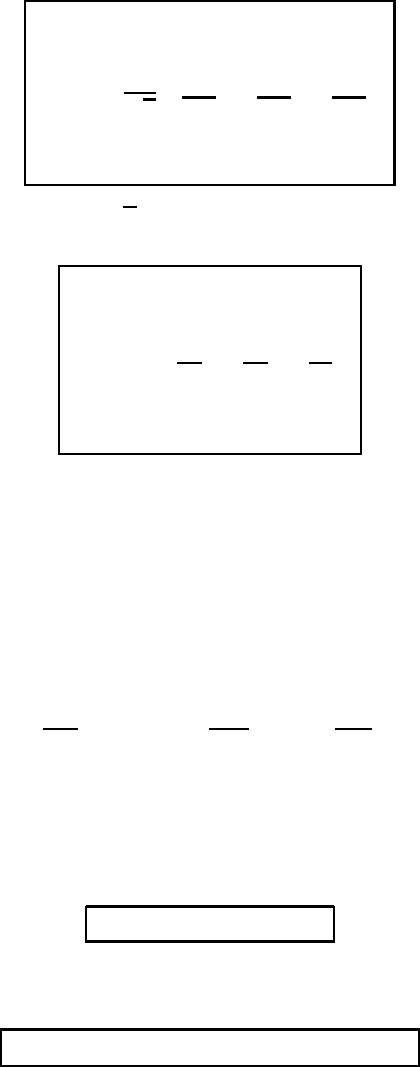
56 Differential relations

which can be written in the convenient determinant form

∇×A =

√



∂

∂q

∂

∂q

∂

∂q



(M3.63)

Since in the Cartesian system

√

g = 1, in this special case we obtain the well-known

formula

∇×A =



ijk

∂

∂x

∂

∂y

∂

∂z



(M3.64)

The vector ∇×A is commonly known as the curl of A or rot A.

M3.5 Additional applications

Of particular interest are the invariants of the unit dyadic and of the gradient of

the position vector. Utilizing the expressions (M3.44) and (M3.48) for the spatial

derivatives of the covariant and the contravariant basis vectors, respectively, we

may write

∇

E = q

∂

∂q

) = q



∂ q

∂q

+ q

∂q



= q



−q



+ q





= 0

(M3.65)

The two terms involving the Christoffel symbols are identical since in the last term

the summation indices m and r may be interchanged without changing the value

of this term. Thus, the gradient of the unit dyadic vanishes and we have

∇·E = 0, ∇×E = 0

(M3.66)

Recalling that according to (M3.30) the gradient of the position vector r is the unit

dyadic, that is ∇r =

E = q

, we immediately obtain

∇·r = q

·q

= 3, ∇×r = q

× q

= 0 (M3.67)

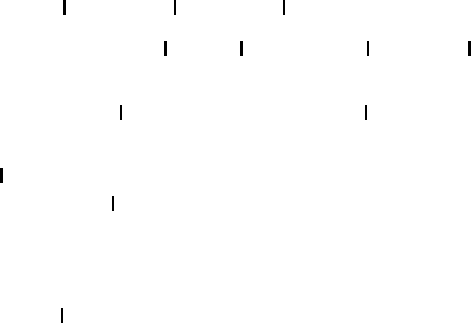
M3.5 Additional applications 57

It will very often be necessary to apply the Hamilton operator to products of

various types of extensive functions. Sometimes this can be very complex. To avoid

errors we must apply the following rules:

(I) As the ﬁrst step we must apply the well-known product rules of differential calculus.

(II) As the second step we must apply the rules of vector algebra with the goal in mind to

obtain a unique and an unmistakeable arrangement of operations.

The following rule helps us to accomplish this task: An arrow placed above any

vector in a product implies that only this vector need be differentiated while the

remaining vectors in the product are treated as constants. As an example consider

the operation

∇(A·

↓

B) =∇(

↓

B·A) = (∇B)·A (M3.68)

The arrow placed above the vector B indicates that the gradient operator is applied

to this vector only. Since we are dealing with a scalar product, the operation is very

simple. When the proper order of the operations is clear we omit the arrow. The

following example implies that only vector A ahead of the gradient symbol is to

be differentiated:

↓

A(∇·B) = (B·∇ )

↓

A = B·∇ A (M3.69)

We must be careful that the dot between the gradient operator and the vector B

does not change its position, otherwise the value of the entire expression will be

changed. When the operation is ﬁnished, the arrow is no longer needed and may

be omitted.

A somewhat more complex example is given by

∇·(A·

) =∇·(

↓

A·) +∇·(A·

↓

)

=∇A··

+ (A·)·



∇=∇A·· + A·(∇·



)

(M3.70)

Note that the term A·

↓

 is a vector so that ∇·(A·

↓

) is a scalar product. Thus we

may rewrite this expression by interchanging the positions of the two vectors ∇

and (A ·

↓

). The curved backward arrow occurring in (M3.70) indicates that the

gradient operates on 

only. Finally, in order to obtain the usual notation without

the backward arrow, in the last expression of (M3.70) we have used the rule (M2.18)

for the multiplication of a vector by a dyadic. Later it will become apparent that

this equation is particularly interesting if A is identiﬁed as the velocity vector v

and the dyadic 

as ∇v. This results in

∇·(v·∇v) =∇v··∇v + v·[∇·(v



∇)] =∇v··∇v + v·∇ (∇·v)(M3.71)

58 Differential relations

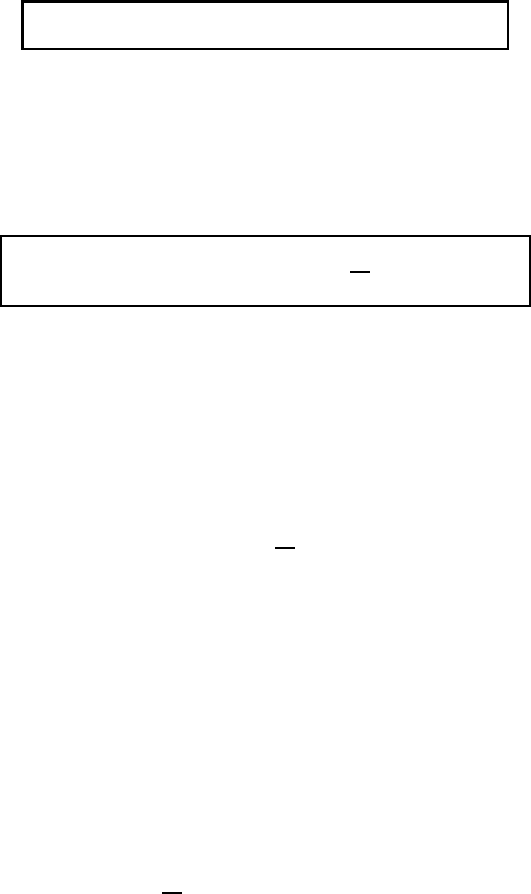
Now consider the expression A ×(∇×B). First of all it should be observed that

the differentiation refers to the vector B. By using Grassmann’s rule (M1.44) we

ﬁnd

A × (∇×B) = (A·B)



∇−A·∇B = (∇B)·A − A·∇B (M3.72)

Replacing A in this equation by the nabla operator yields

∇×(∇×B) =∇(B·



∇) −∇·∇B =∇(∇·B) −∇

(M3.73)

This particular form is often needed.

Equation (M3.72) may be rearranged as

A·∇B = (∇B)·A + (∇×B) × A (M3.74)

Replacing now A and B by v, we ﬁnd the so-called Lamb transformation

v·∇v = (∇v)·v + (∇×v) × v =∇





+ (∇×v) × v

(M3.75)

which is of great importance in dynamic meteorology.

Now we will derive another important formula that will be used in dynamic

meteorology. We start by rearranging (M3.71) into the form

∇v··∇v =∇·(v·∇ v) − v·∇(∇·v)(M3.76)

Utilizing (M3.75), the ﬁrst term on the right-hand side may be rewritten as

∇·(v·∇v) =∇





−∇·[v × (∇×v)] (M3.77)

In this equation the last term on the right-hand side will be evaluated:

∇·[v × (∇×v)] =∇·[

↓

v × (∇×v)] −∇·[

↓

(∇×v) × v]

= (∇×v)·(∇×v) − [∇×(∇×v)]·v

= (∇×v)

− v·[∇×(∇×v)]

= (∇×v)

− v·[∇(∇·v) −∇

(M3.78)

The last equation has been obtained by making use of (M3.73) with B = v. Hence,

(M3.77) may be written as

∇·(v·∇v) =∇





− (∇×v)

+ v·[∇(∇·v)] − v·∇

v (M3.79)

M3.5 Additional applications 59

Substituting this expression into (M3.76) yields the ﬁnal result

∇v··∇v =∇





− (∇×v)

− v·∇

(M3.80)

Finally, we consider an arbitrary ﬁeld vector A, which is assumed to depend on

some scalar functions ψ and χ , whereby these functions depend on the position

and on time, as shown in

A = A[ψ(q

,t),χ(q

,t)] (M3.81)

Now the gradient of A is given by

∇A = q

∂A

∂q

= q



∂A

∂ψ

∂q

∂A

∂χ

∂q



=∇ψ

∂A

∂ψ

+∇χ

∂A

∂χ

(M3.82)

It is important to observe the positions of the vectors forming the dyadics.

In the simple case that A = A[ψ(q

,t)], the gradient of A, the ﬁrst scalar,

and the vector of ∇A are given by

∇A =∇ψ

dψ

, ∇·A =∇ψ ·

dψ

, ∇×A =∇ψ ×

dψ

(M3.83)

The Laplacian of A is obtained from

∇

A =∇·



∇ψ

dψ



=∇

dψ

+∇ψ ·∇



dψ



=∇

dψ

+∇ψ ·



∇ψ

dψ



=∇

dψ

+ (∇ψ)

dψ

(M3.84)

In the ﬁnal step use of the ﬁrst equation of (M3.83) has been made by replacing A

there by the derivative dA/dψ.

60 Differential relations

M3.6 Problems

M3.1: Use generalized coordinates to show that

∇r =

E, ∇(r·r) = 2r, ∇r = e

, ∇





=−

∇·r = 3, ∇×r = 0, ∇·e

, ∇·





= 0, ∇





= 0

M3.2: The potential temperature of dry air is given by θ = T/ where  =

(p/p

)

p,0

is the so-called Exner function. p is the pressure, p

= 1000 hPa, T

the temperature, R

the individual gas constant, and c

p,0

the speciﬁc heat at constant

pressure. Find the gradient of the potential temperature.

M3.3: Assume that a vector W is given by W = r

Ω,whereΩ is a constant

rotational vector. Use generalized coordinates to ﬁnd expressions for

(a) ∇·W, (b) ∇×W, (c) ∇

W, (d) v·∇ W

M3.4: According to a theorem of potential theory, the velocity vector can be split

according to v =−∇×Ψ +∇χ with the additional condition ∇·Ψ = 0. Here

Ψ is a vector (the stream-function vector) and χ is a scalar function (the velocity

potential). You do not need to know the meaning of Ψ and χ to perform the

following differential operations:

(a) ∇·v, (b) ∇×v, (c) ∇

(d) ∇(∇·v), (e) ∇·[

(∇v + v



∇−

∇·vE]

Hint: The Laplace operator and the gradient operator can be interchanged. In

generalized coordinates the validity of this operation is difﬁcult to show, so the

proof will be omitted.

M3.5: Use generalized coordinates to show that ∇·

E = 0.

M3.6: The frictional stress tensor can be written in the form

J =



∇v + v



∇−

∇·v



where η is a scalar coefﬁcient. Use Cartesian coordinates to solve the following

problems.

(a) Show that the trace of

J is zero.

(b) By assuming that w = 0,∂u/∂x= 0,∂u/∂y= 0,∂v/∂x= 0,∂v/∂y= 0,

write

J in matrix form.