Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

M2.2 Special dyadics 31
M2.2.5 The reciprocal dyadic
The unit dyadic
E may be expressed with the help of any three noncoplanar
reciprocal basis vectors. Thus, we may choose the form
E = B
m
B
m
(M2.37)
The reciprocal dyadic
−1
of is defined by
·
−1
= E (M2.38)
If is given in the form = B
m
q
m
then the reciprocal dyadic
−1
must be
−1
= q
m
B
m
(M2.39)
since
·
−1
= B
m
q
m
·q
n
B
n
= B
m
δ
n
m
B
n
= B
m
B
m
= E (M2.40)
In analogy to (M1.55) we may express B
i
as
B
i
=
B
j
× B
k
[B
1
, B
2
, B
3
]
(M2.41)
On substituting (M1.53) and (M2.41) into (M2.39) we immediately recognize that
the reciprocal dyadic
−1
may be formulated in terms of the adjoint dyadic:
−1
=
1
2
(q
m
× q
n
)(B
m
× B
n
)
[q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]
=
a
[q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]
(M2.42)
Without proof we give the following expressions:
(B·D·F)
−1
= F
−1
·D
−1
·B
−1
B
−1
α
= B
−α
B
α
·B
β
= B
α+β
B
0
= E
(M2.43)
which may be generalized to include additional factors. Since dyadics are tensors
of rank two, they can be treated as square matrices, for which the inversion formulas
are derived in any textbook on the subject.
32 Vector functions
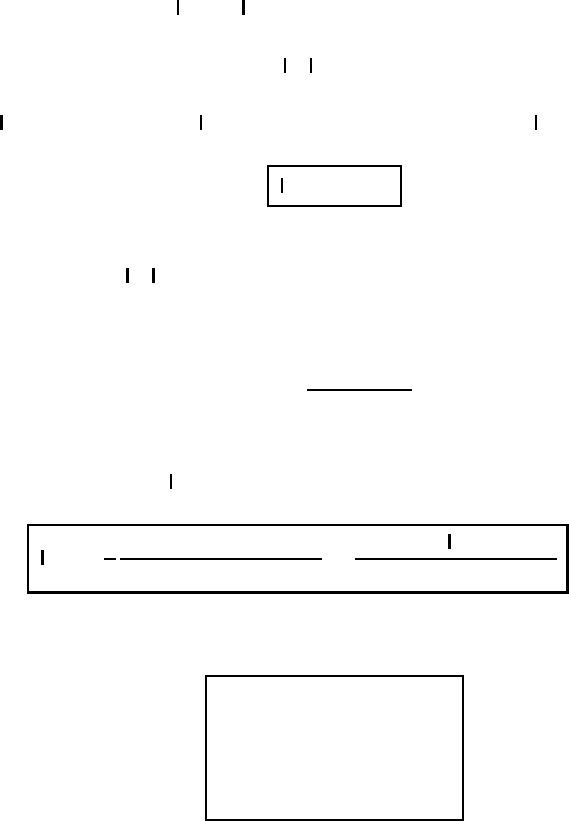
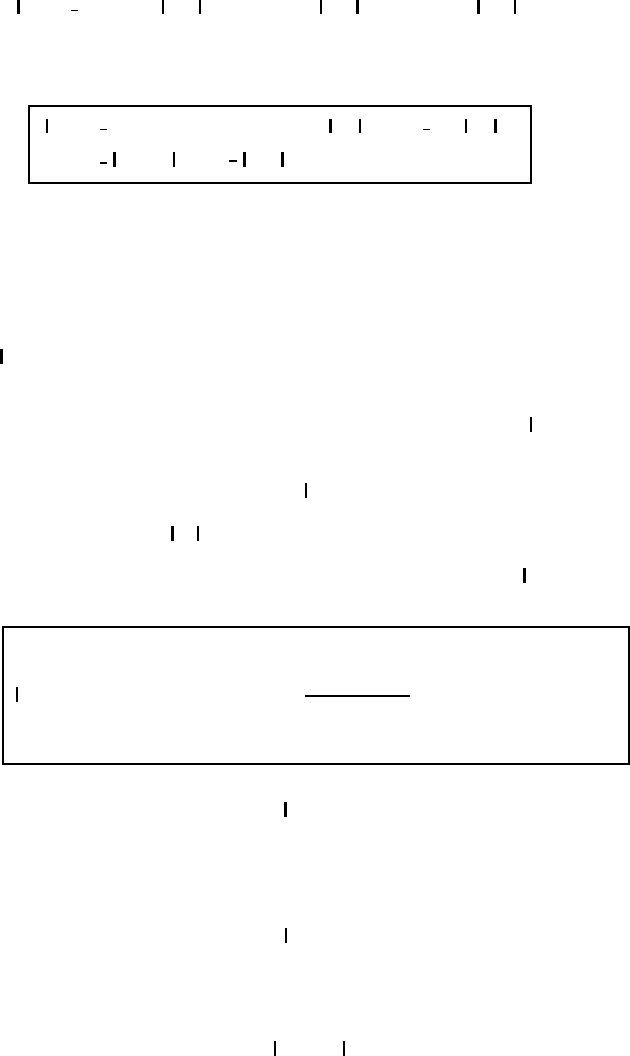
Fig. M2.1 The tensor ellipsoid r·
·r = 1. r
=
·r is perpendicular to the tangentia
l
plane at P .
M2.3 Principal-axis transformation of symmetric tensors
Premultiplication and postmultiplication of the general dyadic by the position
vector r = x
m
i
m
yields
r·
·r = r·
·r + r·
·r = r·
·r (M2.44)
The term r·
·r of this expression vanishes since the scalar premultiplication and
postmultiplication of an antisymmetric dyadic by an arbitrary vector must vanish
in order to avoid the following contradiction:
A·
·A = (A·
)·A = A·(A·
) = A·(
·A) =−A·
·A = 0(M2.45)
On substituting (M2.22) into (M2.44) we obtain the quadratic form
F = r·
·r = x
r
i
r
·B
mn
i
m
i
n
·x
s
i
s
= x
r
x
s
B
mn
δ
m
r
δ
n
s
= x
m
x
n
B
mn
= B
11
x
2
1
+ B
22
x
2
2
+ B
33
x
2
3
+ 2B
12
x
1
x
2
+ 2B
23
x
2
x
3
+ 2B
13
x
1
x
3
(M2.46)
It can be seen that the constant coefficients B
ij
of the symmetric dyadic determine
the type of the quadratic surface. The tensor surface F may be an ellipsoid, a
hyperboloid, or a paraboloid. Most applications from physics deal with ellipsoids
so that collectively we speak of tensor ellipsoids of the symmetric tensor. As
a representative of the tensor ellipsoid we select F = 1. The position vector r
extends from the origin of the ellipsoid to some point P on the ellipsoidal surface;
see Figure M2.1. Since the point −r is also located on the tensor surface, we speak
of a midpoint surface.
Let us now investigate the transformation r
=
·r. There exist special directions
of r for which r and r
are parallel vectors. These directions are known as the
M2.3 Principal-axis transformation of symmetric tensors 33
principal-axis directions. The corresponding mathematical statement is given by
r
=
· r = λr or (
− λE)·r = 0(M2.47)
where the scalar λ is the eigenvalue of the operator
. An equation of this form is
known as an eigenvalue equation or characteristic equation. In coordinate notation
this eigenvalue equation can be written as
(B
mn
− λδ
mn
)x
n
= 0(M2.48)
For the variables x
j
this is a linear homogeneous system that has nontrivial solutions
only if the determinant of the system vanishes, namely
B
11
− λB
12
B
13
B
21
B
22
− λB
23
B
13
B
23
B
33
− λ
= 0(M2.49)
This results in an eigenvalue equation of third order, where the λ
i
are the eigenvalues
of the operator
. Every solution vector r
i
of
(
− λ
i
E)·r
i
= 0(M2.50)
that differs from the zero vector is an eigenvector corresponding to the eigenvalue
λ
i
. From linear algebra we know that the eigenvalues of a symmetric matrix are
real and that the eigenvectors of such a matrix can always be chosen to be real.
Furthermore, a real symmetric matrix is diagonalizable. Moreover, eigenvectors of
such a matrix corresponding to distinct eigenvalues are orthogonal.
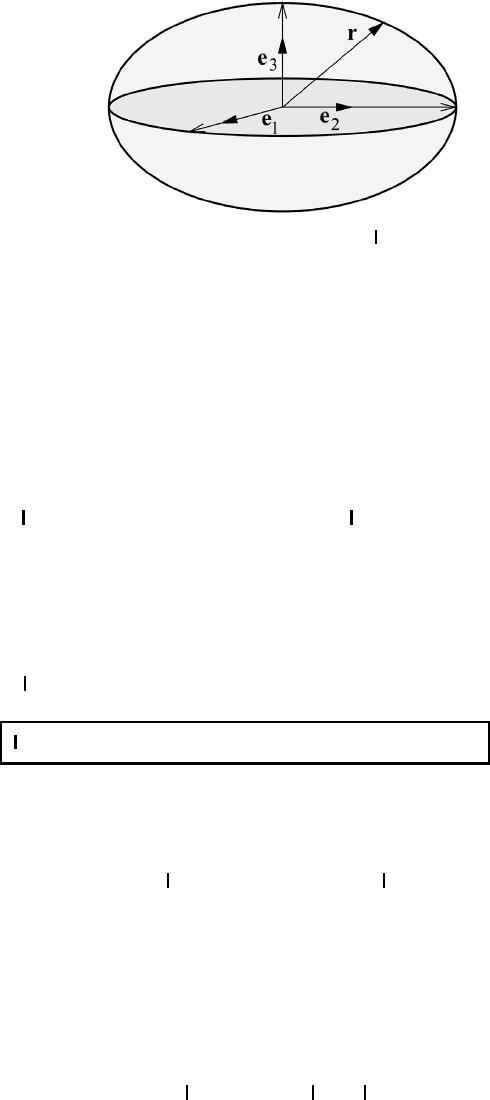
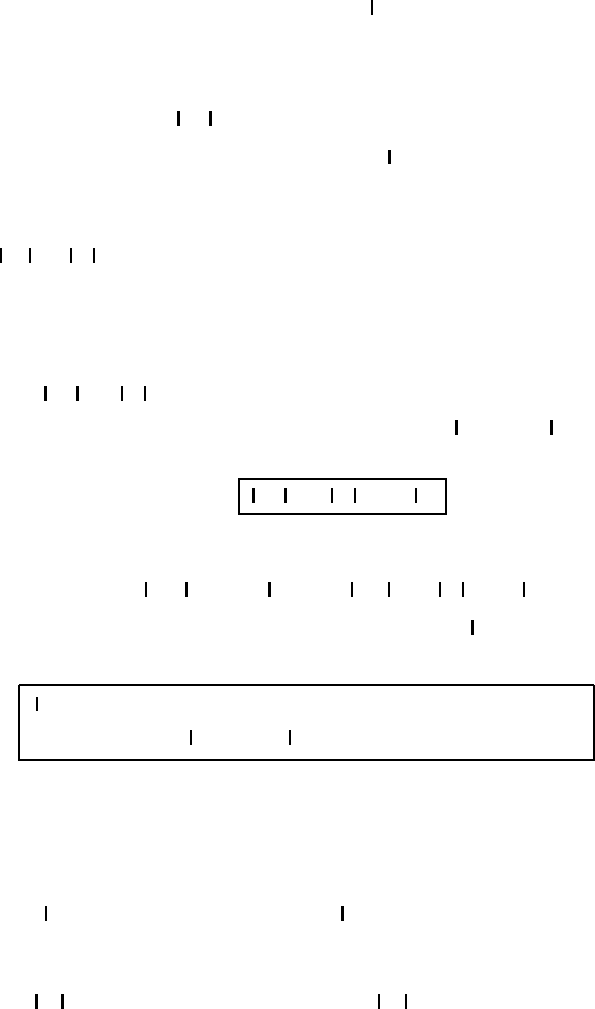
Let us now briefly consider the principal-axis directions. The symmetric dyadic
= B
mn
i
m
i
n
can be reduced to the simple form
= λ
1
e
1
e
1
+ λ
2
e
2
e
2
+ λ
3
e
3
e
3
(M2.51)
since symmetric matrices can be diagonalized. The basis vectors e
i
appearing in
(M2.51) are directed along the principal axes of the tensor ellipsoid as shown in
Figure M2.2. By expressing the position vector r as
r = e
1
ξ
1
+ e
2
ξ
2
+ e
3
ξ
3
(M2.52)
we obtain the principal-axes form of the tensor ellipsoid
F = r·
·r = λ
1
ξ
2
1
+ λ
2
ξ
2
2
+ λ
3
ξ
2
3
= 1(M2.53)
The particular tensor ellipsoid of interest to our future studies is the stress tensor or
the stress dyadic. We will return to this section later when we discuss the viscous
forces acting on a surface element.
34 Vector functions
Fig. M2.2 Eigenvectors e
i
of the tensor ellipsoid r ·
·r = 1 corresponding to the
eigenvalues λ
i
.
M2.4 Invariants of a dyadic
Dyadics are extensive quantities that are independent of a coordinate system. If
the general multiplication is changed to scalar or vectorial multiplication, we find
expressions that again are independent of the coordinate system. Such coordinate-
independent expressions are called invariants of a dyadic. The starting point of our
discussion is the complete dyadic
= B
n
q
n
= B
m
n
q
m
q
n
with B
i
= ·q
i
= B
m
i
q
m
(M2.54)
M2.4.1 The first scalar of a dyadic
On taking the scalar product of the vectors appearing in the dyadic we obtain the
first scalar
I
of the dyadic,
I
= B
n
·q
n
= B
m
n
q
m
·q
n
= B
m
n
δ
n
m
= B
1
1
+ B
2
2
+ B
3
3
(M2.55)
This is the trace of the coefficient matrix (B
i
j
). Owing to the validity of the
commutative law for the scalar product (M1.14), we obtain
I
= B
n
·q
n
= q
n
·B
n
=
I
(M2.56)
Application of (M2.55) to the unit dyadic yields the interesting result
E
I
= q
n
·q
n
= q
1
·q
1
+ q
2
·q
2
+ q
3
·q
3
= 3(M2.57)
According to (M2.28) the diagonal elements of an antisymmetric dyadic vanish so
that
I
= 0 =⇒
I
=
I
(M2.58)
M2.4 Invariants of a dyadic 35
In thermodynamics and elsewhere it is customary to decompose the symmetric
dyadic
into an isotropic symmetric part
iso
and an anisotropic symmetric part
aniso
:
=
iso
+
aniso
requiring that (
iso
)
I
=
I
=⇒ (
aniso
)
I
= 0(M2.59)
We now rewrite
in the form
= αE + (
− αE)(M2.60)
where α is a scalar that needs to be determined. The first term on the right-hand side
of (M2.60) represents the isotropic part while the second term is the anisotropic
part. Hence, α is found from
(
− αE)
I
=
I
− 3α = 0 =⇒ α =
I
/3(M2.61)
and the isotropic and anisotropic parts of
are given by
iso
=
I
3
E,
aniso
=
−
I
3
E (M2.62)
Utilizing (M2.27), (M2.59), and (M2.62) we may express any complete dyadic in
the form
=
+
=
iso
+
aniso
+
=
I
3
E +
−
I
3
E
+
(M2.63)
M2.4.2 The vector of a dyadic
The vector of a dyadic is defined by placing the cross, denoting vectorial multipli-
cation, between the members of each pair of vectors. Application of (M1.53) and
observing (M1.57) results in
×
= B
n
× q
n
= B
mn
q
m
× q
n
=
1
√
g
(B
23
− B
32
)q
1
+ (B
31
− B
13
)q
2
+ (B
12
− B
21
)q
3
(M2.64)
It is immediately obvious that
×
= B
n
× q
n
=−q
n
× B
n
=−
×
(M2.65)
36 Vector functions
From (M2.64) it follows immediately that the vector of a symmetric dyadic must
vanish:
×
= 0 =⇒
×
=
×
(M2.66)
Of particular interest is the following equation:
E × B = B × E
(M2.67)
indicating that vectorial multiplication of the unit dyadic
E by an arbitrary vector
B is commutative. In order to give a very brief proof, we assume that B = q
1
,
yielding
E × q
1
= q
n
q
n
× q
1
= q
2
(q
2
× q
1
) + q
3
(q
3
× q
1
) =−q
2
q
3
√
g + q
3
q
2
√
g
q
1
× E = q
1
× q
n
q
n
= (q
1
× q
2
)q
2
+ (q
1
× q
3
)q
3
= q
3
q
2
√
g − q
2
q
3
√
g
=⇒
E × q
1
= q
1
× E
(M2.68)
In the general case the vector B consists of three components so that the proof is
more lengthy but not more difficult.
Of some interest to our future studies is the cross product of the unit dyadic with
the vector of the dyadic
. By employing the Grassmann rule (M1.44) we can
easily carry out the operations
E ×
×
= E × (B
n
× q
n
) = q
m
q
m
× (B
n
× q
n
)
= q
m
(q
m
·q
n
)B
n
− q
m
(q
m
·B
n
)q
n
= q
n
B
n
− E·B
n
q
n
= q
n
B
n
− B
n
q
n
=−2
(M2.69)
This provides a new way to express an antisymmetric dyadic in the form
= −
1
2
E ×
×
=−
1
2
×
× E (M2.70)
Taking the scalar product of an antisymmetric dyadic with a vector B gives an
interesting and useful relation that may be helpful if complicated expressions have
to be manipulated:
·B = −
1
2
(
×
× E)·B =−
1
2
×
× B =
1
2
B ×
×
(M2.71)
M2.4.3 The second scalar of a dyadic
Another invariant is the second scalar of a dyadic, which by definition is the first
scalar of the adjoint dyadic. By employing equation (M2.31) we find
II
=(
a
)
I
= (q
1
× q
2
) · (B
1
× B
2
) + (q
2
× q
3
) · (B
2
× B
3
)
+ (q
3
× q
1
) · (B
3
× B
1
)
(M2.72)
M2.4 Invariants of a dyadic 37
The cross products of the contravariant basis vectors appearing in this equation can
be removed with the help of equation (M1.53). By obvious steps we obtain
II
=
1
[q
1
, q
2
, q
3
]
q
3
·(B
1
× B
2
) + q
1
·(B
2
× B
3
) + q
2
·(B
3
× B
1
)
=
1
[q
1
, q
2
, q
3
]
([q
1
, B
2
, B
3
] + [B
1
, q
2
, B
3
] + [B
1
, B
2
, q
3
])
(M2.73)
where the rules associated with the scalar triple product have been applied to
obtain the second equation. Since according to (M2.9) B
i
= B
n
i
q
n
, with the help
of (M1.38) we find for the first scalar triple product of (M2.73)
[q
1
, B
2
, B
3
] = [q
1
, q
2
, q
3
]
100
B
1
2
B
2
2
B
3
2
B
1
3
B
2
3
B
3
3
= [q
1
, q
2
, q
3
]
B
2
2
B
3
2
B
2
3
B
3
3
(M2.74)
Expressing the remaining terms in (M2.73) in the same way yields
II
=
B
1
1
B
2
1
B
1
2
B
2
2
+
B
1
1
B
3
1
B
1
3
B
3
3
+
B
2
2
B
3
2
B
2
3
B
3
3
(M2.75)
showing that the second scalar of the dyadic
is the sum of three second-order
determinants.
Let us now consider the determinant of the matrix (B
i
j
). From (M2.75) we easily
recognize that the second scalar of the dyadic
is the sum of the cofactors of the
elements forming the main diagonal of B:
II
= M
3
3
+ M
2
2
+ M
1
1
(M2.76)
Since the reversal of factors in (M2.72) cannot yield a different result, we recognize
that the second scalar of the conjugate dyadic is identical with the second scalar of
the dyadic
itself:
II
=
II
(M2.77)
Without verification we accept
II
=
II
+
II
(M2.78)
The proof is somewhat lengthy but not particularly instructive.
38 Vector functions
Before continuing with additional operations involving the second scalar, it will
be profitable to introduce the so-called double scalar product, which is also known
as the double-dot product. To begin with, consider the scalar multiplications A··B.
Since the scalar product of a vector with a dyadic results in a new vector, the product
can be formed in two ways:
A·
·B = A·(·B) = (·B)·A
A·
·B = (A·)·B = B·(A·)
(M2.79)
Obviously, the scalar product of vectors A and B is meaningless in these two
expressions. Thus, it is customary to introduce the double-dot or double scalar
product
(
·B)·A = ··BA, B·(A·) = BA·· (M2.80)
On combining (M2.79) and (M2.80) we obtain the defining equation of the double
scalar product:
A··B = BA·· = ··BA
(M2.81)
Some authors place the two dots vertically so that the double-dot product looks
like a ratio symbol.
Of considerable interest to our studies is the second scalar of an antisymmetric
dyadic. From (M2.8) we have B
i
= ·q
i
.If =
we find from (M2.66) and
(M2.71) the relations
·q
i
= B
i
=
1
2
q
i
×
×
=
1
2
q
i
×
×
(M2.82)
Substituting this expression into (M2.73) yields
II
=
1
4[q
1
, q
2
, q
3
]
{
q
3
·[(q
1
×
×
) × (q
2
×
×
)] + q
2
·[(q
3
×
×
) × (q
1
×
×
)]
+ q
1
·[(q
2
×
×
) × (q
3
×
×
)]
}
(M2.83)
Application of (M1.50) to each term within the braces of (M2.83) results in a total
of six terms. Three terms vanish since in these terms the same vector appears twice
in the scalar triple product. For the first term, this is explicitly shown in
(q
1
×
×
) × (q
2
×
×
) = [q
1
,
×
,
×
]q
2
− [q
1
,
×
, q
2
]
×
=−[q
1
,
×
, q
2
]
×
(M2.84)
Performing the same operation with the other two terms in (M2.83) and using the
rules of the scalar triple product, we find
II
=
1
4[q
1
, q
2
, q
3
]
(q
3
·[q
1
, q
2
,
×
]
×
+ q
2
·[q
3
, q
1
,
×
]
×
+ q
1
·[q
2
, q
3
,
×
]
×
)
(M2.85)
M2.4 Invariants of a dyadic 39
Utilizing the defining relation (M1.55) for the contravariant basis vectors results in
II
=
1
4
q
3
·(q
3
·
×
)
×
+ q
2
·(q
2
·
×
)
×
+ q
1
·(q
1
·
×
)
×
(M2.86)
In this equation we introduce the double scalar product according to (M2.81) as
well as the definition of the unit dyadic (M1.80), thus obtaining the final result
II
=
1
4
(q
1
q
1
+ q
2
q
2
+ q
3
q
3
)··
×
×
=
1
4
E··
×
×
=
1
4
×
·E·
×
=
1
4
×
·
×
(M2.87)
M2.4.4 The third scalar of a dyadic
By introducing the reciprocal systems (M1.53) and (M2.41) into the definition of
the adjoint dyadic (M2.31), we obtain
a
= q
3
B
3
[q
1
, q
2
, q
3
][B
1
, B
2
, B
3
] + q
1
B
1
[q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]
+ q
2
B
2
[q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]
= [q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]q
n
B
n
= [q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]
−1
(M2.88)
where the reciprocal dyadic has been used according to (M2.39). Scalar multipli-
cation of this expression by the dyadic
yields
·
a
= [q
1
, q
2
, q
3
][B
1
, B
2
, B
3
]E (M2.89)
This is the defining equation for the third scalar of the dyadic ,whichmaybe
written as
III
= [q
1
, q
2
, q
3
][B
1
, B
2
, B
3
] =
[B
1
, B
2
, B
3
]
[q
1
, q
2
, q
3
]
=
B
1
1
B
1
2
B
1
3
B
2
1
B
2
2
B
2
3
B
3
1
B
3
2
B
3
3
(M2.90)
Hence, the third scalar of the dyadic is the determinant of the coefficient matrix
(B
i
j
).
We conclude this section by stating two important special cases. From equation
(M2.26) for the antisymmetric dyadic we immediately see that
III
= 0(M2.91)
since the determinants of q
n
B
n
and B
n
q
n
are equal. Finally, owing to the fact that
Det(B
i
j
) = Det(B
j
i
), we obtain
(
)
III
=
III
(M2.92)
40 Vector functions
M2.5 Tensor algebra
We conclude this chapter by presenting some interesting and useful tensor opera-
tions. Let us consider a dyadic in the form
= B
n
q
n
. The double scalar product
involving the same dyadic twice is of some interest to our studies. By connecting
the exterior and interior vectors by the dots representing the scalar multiplication
we find
·· = B
r
q
r
··B
n
q
n
= (q
n
·B
r
)(q
r
·B
n
)(M2.93)
Using this result together with the first scalar
I
= B
n
·q
n
= q
n
·B
n
we may easily
obtain the following determinant:
·· −
I
I
= (q
n
·B
r
)(q
r
·B
n
) −(q
n
·B
n
)(q
r
·B
r
) =
q
n
·B
r
q
n
·B
n
q
r
·B
r
q
r
·B
n
(M2.94)
Applying equation (M1.48) and utilizing the definitions of the adjoint dyadic
(M2.30) and of the second scalar (M2.72) yields
·· −
I
I
= (q
n
× q
r
)·(B
r
× B
n
)
=−(q
n
× q
r
)·(B
n
× B
r
) =−2(
a
)
I
=−2
II
(M2.95)
so that
·· =
I
I
− 2
II
(M2.96)
Recall that the first scalar of an antisymmetric dyadic is zero; see (M2.58). Hence,
we find
··
=−2
II
,
··
=
I
I
− 2
II
(M2.97)
Next let us consider the vector product of the dyadic
with the vector (C ×D).
By applying the Grassmann rule we find
× (C × D) = B
n
[q
n
× (C × D)] = B
n
[(q
n
·D)C − (q
n
·C)D]
= (
·D)C − (·C)D
(M2.98)
Changing the position of the parentheses will also change the result.
Operations involving dyadics require some care, as the following examples show.
While the scalar product of two vectors is commutative, the scalar product of a
vector and a dyadic is not commutative:
C·
= C·(B
n
q
n
) = (C·B
n
)q
n
,·C= (B
n
q
n
)·C = (q
n
·C)B
n
(M2.99)
Moreover, the scalar product of two dyadics is not commutative either:
· = (AB)·(CD) = (B·C)AD,·= (CD)·(AB) = (D·A)CB
(M2.100)
