Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

M2.5 Tensor algebra 41

Often it may be desirable to involve the scalar measure numbers in the scalar

product of two dyadics. Usually it is of advantage to use the reciprocal system of

basis vectors:



· = A

·q

= A

= C

(M2.101)

The two scalar quantities are summed over n to give C

= A

. This result

corresponds to the rules of matrix multiplication. The elements of the ith row are

multiplied by the elements of the j th column.

Next we wish to point out that the conjugate of the scalar product of two dyadics

is equal to the scalar product of the individual conjugate dyadics:





· =



·



 (M2.102)

Of great importance is the following equation:

E· = ·E =  (M2.103)

showing that the scalar product of a dyadic with the unit dyadic results in the dyadic

itself. Therefore, taking the scalar product of an abitrary dyadic with the unit dyadic

is commutative. The proofs of (M2.102) and (M2.103) are straightforward and are,

therefore, omitted.

Consider the double-dot product of 

= B

and  = D

. The double-dot

product of the two dyadics involves the scalar product of reciprocal basis vectors:



·· = B

··D

= B

··D

= B

·q

)(q

·q

) = B

= C

(M2.104)

Hence, it can be seen that the double-dot product simply gives the trace of the

matrix (C

). From (M2.81) and (M2.104) we see that

·· =  ·· = (·)

= C

(M2.105)

On substituting into this expression 

= E we obtain the important result

··E = E·· = (·E)

= 

(M2.106)

The validity of





··



 = ·· (M2.107)

may easily be veriﬁed and is left as a simple excercise.

Of particular interest, as we shall see in our study of thermodynamics, is the

double scalar product of a symmetric and an antisymmetric dyadic. Using equation

(M2.107) and applying the deﬁnitions of the symmetric and antisymmetric dyadics

leads us to conclude that the double scalar product must vanish for consistency, as

shown in





··









··







=−



··



= 0

(M2.108)

42 Vector functions

M2.6 Problems

M2.1: Show that

A × r = r·



where 



is an antisymmetric dyadic. Find 



M2.2: By utilizing (M2.97) show that 



··



is positive deﬁnite.

M2.3: Show the validity of the following expressions:

(a) 

· = ·

, (b)



(

)

= 

·

M2.4: Find the eigenvalues and eigenvectors of the eigenvalue problem

(

− λE)·r = 0, (

) =







2 −10

−12−1

0 −12







where







is the matrix corresponding to . Hint: One eigenvalue is λ

= 2.

Differential relations

Many mathematical statements of the laws of physics involve differential or integral

expressions. Therefore, we must be able to differentiate and integrate expressions

involving vectors and dyadics. While in the Cartesian nonrotating coordinate sys-

tem the basis vectors i, j,andk may be treated as constants, basis vectors in

generalized coordinate systems depend on spatial coordinates and may depend on

time.

M3.1 Differentiation of extensive functions

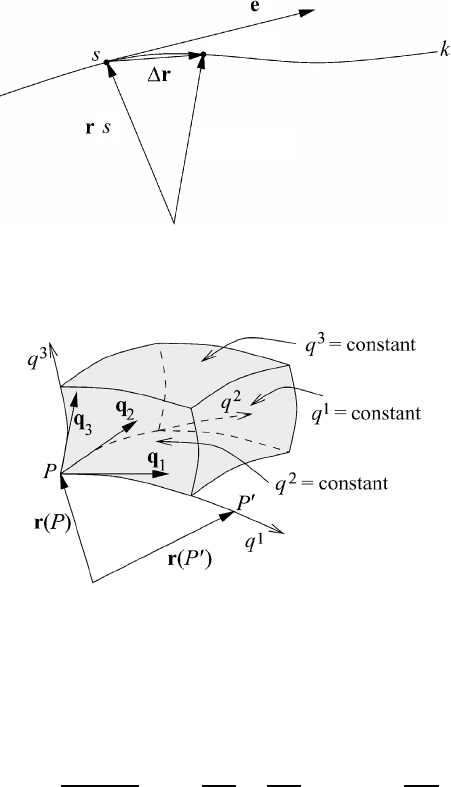
Let us consider a curve k in space as shown in Figure M3.1. From some origin

we draw the position vector r(s) to the point s on the curve. Upon advancing the

arclength s along the curve, the new position vector will be r(s +s). Applying

the deﬁnition of the derivative

= lim

s→0

r

s

= lim

s→0

s e

r

s

= e

r

= e

(M3.1)

we obtain the unit tangent vector e

on the curve at point s.

When we are differentiating products involving vectors and dyadics we must

observe the sequence of the factors. An example is given by

(A·

·B) =

·

·B + A·

d

·B + A·

(M3.2)

Suppose that we wish to differentiate the vector A with respect to the parameter s.

In this case we must differentiate not only the scalar measure number A

but also

the basis vector q

, since this vector varies in space:

) =

+ A

(M3.3)

44 Differential relations

)(

( )

r(s+∆s)

s+∆ s

Fig. M3.1 The unit tangent vector e

along a curve k in space.

Fig. M3.2 A volume element of the generalized q

system.

An important example is the scalar product of the unit vectors, e

·e

. Differentiation

of this expression with respect to s shows that the derivative de

/ds is perpendicular

to e

·e

= 1 =⇒

d(e

·e

)

= e

·e

= 2e

= 0(M3.4)

Let us now consider a volume element deﬁned by sections of the contravariant

curvilinear coordinate lines q

as shown in Figure M3.2. Note that the coordinate

line q

is formed by the intersection of the coordinate surfaces q

= constant

and q

= constant in the same way as that in which the x-axis of the orthogonal

Cartesian system is formed by the intersection of the surfaces y = constant and

z = constant. Analogously, the coordinate lines q

and q

areformedbythein-

tersection of the two other coordinate surfaces. The covariant basis vectors q

are

tangent vectors along the respective coordinate lines. The orientation of the basis

vectors q

at a given point P differs from the orientation of the basis vectors at

another point P



. All vectors existing at point P have to be deﬁned with respect

M3.1 Differentiation of extensive functions 45

to the basis existing at that point. In general, every point P



that is separated by a

ﬁnite distance from point P has a different basis so that all vectors deﬁned at point



must be expressed in terms of the basis existing at P



In the general q

-coordinate system all quantities depend on the spatial coordi-

nates q

(i = 1, 2, 3) and on time t. Hence, we write

ψ = ψ(q

,t) = ψ(q

,t)

A = A

= A

,t)q

,t)



= φ

,t)q

,t)

(M3.5)

showing the explicit dependency of ψ, A

, φ

and of the basis vectors q

, q

(i = 1, 2, 3) and t.

According to the rules of differential calculus, we may write the individual total

differentials of ψ, A,

in the forms

dψ =

∂ψ

∂t

dt +

∂ψ

∂q

dA =

∂A

∂t

dt +

∂A

∂q

d =

∂

∂t

dt +

∂

∂q

(M3.6)

We often call these expressions the total differentials or sometimes the individual

differentials of the corresponding variables. It can be seen that the total differential

consists of two parts. The ﬁrst term represents the change with time of the variable

at a ﬁxed point in space. Usually the partial derivative with respect to time ∂/∂t

is called the local time derivative. The second terms on the right-hand sides of

(M3.6) are the so-called geometric differentials of the variables, which are usually

abbreviated as follows:

ψ =

∂ψ

∂q

A =

∂A

∂q

 =

∂

∂q

(M3.7)

Now we wish to investigate the relationship between the position vector r and

the basis vectors. Let us begin with the simple orthogonal Cartesian coordinate

system. For a ﬁxed time the differential dr of the position vector r = r(x

)

46 Differential relations

can be written as

dr = i

= i

+ i

∂r

∂x

∂r

∂x

∂r

∂x

∂r

∂x

(M3.8)

By comparing the differentials dx

of this equation we obtain the basic deﬁnition

of the unit vectors in the Cartesian system:

∂r

∂x

, i

∂r

∂x

, i

∂r

∂x

(M3.9)

Similarly, by expressing the position vector in the general curvilinear coordinate

system, we ﬁnd for a ﬁxed time t

dr = q

∂r

∂q

(M3.10)

and the basic deﬁnition of the covariant basis vector q

∂r

∂q

(M3.11)

The unit vector e

is given as

√

∂r

∂q

(M3.12)

Using the deﬁnition (M3.11), the scalar triple product formed by the covariant basis

vectors may be written as

√

= [q

, q

] =



∂r

∂q

∂r

∂q

∂r

∂q



(M3.13)

and, by means of equation (M1.40), in the explicit form

√



∂x

∂q

∂x

∂q

∂x

∂q

∂x

∂q

∂x

∂q

∂x

∂q

∂x

∂q

∂x

∂q

∂x

∂q



∂(x

)

∂(q

)



(M3.14)

Here and in the following, subscripts q or x (or others) denote the particular coordinate system in which the

corresponding variable has to be evaluated. They will, however, be used only if confusion is likely.

M3.1 Differentiation of extensive functions 47

The determinant of this expression is known as the functional determinant of the

transformation from the initial Cartesian x

-coordinate system to the general q

system. The term

√

is the functional determinant of the Cartesian system with

√

= [i

, i

] = 1. The g

of the square of the functional determinant are

= q

·q

∂r

∂q

∂r

∂q

∂i

∂q

∂i

∂q

∂x

∂q

∂x

∂q

(M3.15)

Whenever the relationship between the Cartesian x

-coordinate system and the q

system is given, it is a simple matter to evaluate this equation.

In analogy to the deﬁnition of the covariant basis vector q

we deﬁne the con-

travariant basis vector q

. From the basic deﬁnition

dr =

∂r

∂q

= q

(M3.16)

and comparing the coefﬁcients of the differential dq

, we easily ﬁnd

∂r

∂q

= g

(M3.17)

where the second equality is the lowering rule according to (M1.84). If the three

covariant basis vectors q

are known as well as the contravariant metric fundamental

quantities g

, then the basis vectors q

may be computed.

There is a very important point that needs to be mentioned. The contravariant

coordinate lines of the curvilinear system are continuous coordinate lines so that

∂

∂q

∂

∂q

(M3.18)

applies. In this case the order of the partial derivatives is immaterial. Owing to the

properties of the reciprocal coordinate systems, the covariant coordinate lines can

be deﬁned only piecewise. Therefore, as is shown in textbooks on analysis, the

order of the differentiation cannot be interchanged:

∂

∂q

=

∂

∂q

(M3.19)

For this reason we prefer partial derivatives with respect to the contravariant co-

ordinates q

. In a later chapter we will encounter this situation involving (M3.19)

when we are dealing with natural coordinates.

48 Differential relations

Fig. M3.3 The geometric meaning of the gradient operator.

M3.2 The Hamilton operator in generalized coordinate systems

Let us reconsider the geometric differential of a scalar ﬁeld function as given in

(M3.7). By inserting the scalar product q

·q

, which does not change the meaning

of d

ψ, we obtain

ψ =

∂ψ

∂q



i=1

∂ψ

∂q



i=1



∂ψ

∂q







=∇ψ ·dr (M3.20)

Here we have introduced the Hamilton operator ∇, which is also known as the

gradient operator,thedel operator,andthenabla operator. Thus, in general

coordinates we deﬁne ∇ by

∇=q

∂

∂q

= q

∇

, ∇

∂

∂q

(M3.21)

where we have also introduced the symbol ∇

to remind the reader that the partial

derivative ∂/∂q

is a covariant expression while q

itself is a contravariant coordi-

nate. The meaning of the nabla operator is twofold: First, it is a vector; and second,

it is a differential operator.

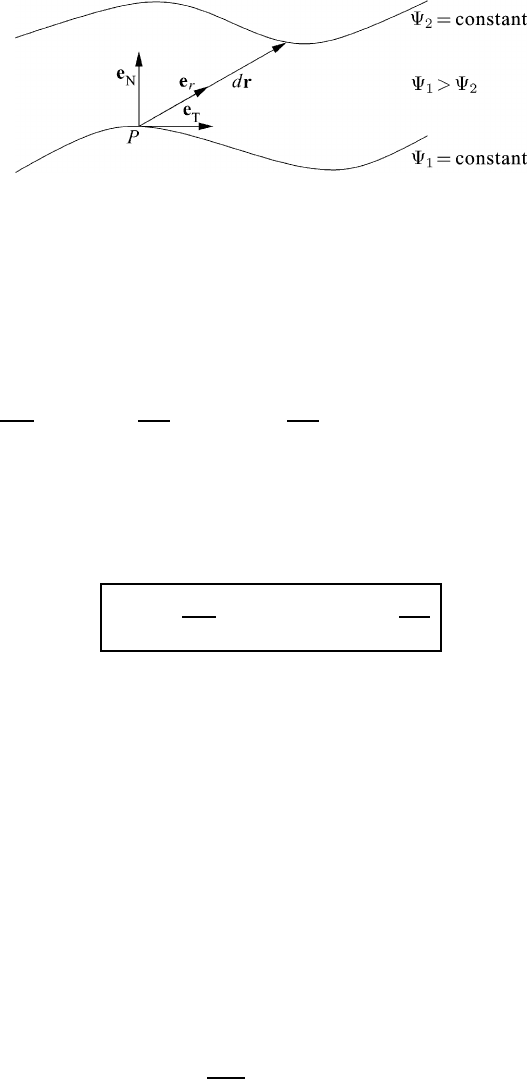
Now we consider the two scalar surfaces shown in Figure M3.3. At the point P

we construct the displacement vector dr = e

dr as well as the unit normal vector

and a unit tangent vector e

along the surface ψ

= constant. These two unit

vectors are perpendicular to each other.

We slightly rewrite equation (M3.20) in the form

ψ = dr·∇ψ = e

dr·∇ψ (M3.22)

so that the geometric change d

ψ/dr is expressed by

= e

·∇ψ (M3.23)

M3.2 The Hamilton operator in generalized coordinate systems 49

If we select the displacement vector dr at P along the surface ψ

= constant, i.e.

= e

, then the geometric change vanishes:

·∇ψ = 0(M3.24)

Therefore, the vectors ∇ψ and e

are perpendicular to each other and ∇ψ is parallel

to the unit normal vector e

∇ψ = e

∇ψ

(M3.25)

that is ∇ψ is perpendicular to the surface ψ = constant. Moreover, choosing

dr = e

means that the magnitude of ∇ψ corresponds to the geometric change

ψ along e

= e

·∇ψ =

∇ψ

(M3.26)

If the ψ-surfaces are closely spaced, then the ψ-gradient is strong and vice versa.

Let us return to the contravariant basis vectors q

, whose directions are known if

the directions of the covariant basis vectors q

are known, as follows from (M1.55)

for the reciprocal systems. By utilizing the deﬁnition of the nabla operator we

have another way to obtain the direction of the contravariant basis vectors. From

(M3.21) it follows immediately that

∇q

= q

∂q

= q

(M3.27)

Often it is desirable to express the gradient operator in terms of the unit vectors

instead of employing the general basis vectors q

. By obvious steps we introduce

the unit vector e

, which automatically leads to the introduction of the covariant

physical measure numbers ∇

of the Hamilton operator:

∇



∇

= e

∇

= e

∂

∂q

with ∇



∇

(M3.28)

Whenever we are dealing with orthogonal systems, it is advantageous to employ

the gradient operator in the form

∇=e

∂

∂q

= e

∇

(M3.29)

Application of the gradient operator to the position vector r yields the unit

dyadic

∇r = q

∂r

∂q

= q

= E

(M3.30)

50 Differential relations

where use of (M3.11) has been made. In the special case of the orthogonal Cartesian

system we obtain

∇r =



∂

∂x

+ j

∂

∂y

+ k

∂

∂z



(ix + jy + kz) = ii + jj + kk =

E (M3.31)

Let us now return to the total derivatives (M3.6). Introducing the velocity

vector v,

v =

= ˙q

(M3.32)

we may write

∂ψ

∂q







∂ψ

∂q



= v·∇ψ (M3.33)

The scalar product v·∇ψ is known as the advection term. Substituting (M3.33) and

corresponding expressions for A and 

into (M3.6) yields

dψ

∂ψ

∂t

+ v·∇ψ

∂A

∂t

+ v·∇A

d

∂

∂t

+ v·∇

(M3.34)

These equations are known as the Euler development of the corresponding variables.

The Euler development applies not only to scalar ﬁeld functions, vectors, and

dyadics, but also to higher-order tensors.

Before concluding this section let us brieﬂy apply Euler’s development to the

vector A:



∂A

∂t



+ ˙q

∂A

∂q



∂A

∂t



+ ˙q

∂A

∂q

(M3.35)

As will be realized by now, in contrast to the Cartesian coordinate system, the basis

vectors q

of the general q

system are functions of the spatial coordinates q

and

of time. Thus, in the general case the gradient of the vector A, which is also known

as the local dyadic of A, must be written as

∇A =∇(A

) = (∇A

+ A

(∇q

)

= q

∂A

∂q

= q

∂A

∂q

+ A

∂q

(M3.36)