Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

M6.6 The general form of the budget equation 101
M6.6 The general form of the budget equation
Theoretical considerations often require the use of budget equations to study the
behavior of certain physical quantities such as mass, momentum, and energy in its
various forms. The purpose of this section is to derive the general form of a balance
or budget equation for these quantities.
Usually any extended part of the atmospheric continuum will be inhomogeneous.
To handle an inhomogeneous section of the atmosphere we mentally isolate a
sizable fluid volume V that is surrounded by an imaginary surface S. Anything
within S belongs to the system; the surroundings or the outside world is found
exterior to S. Processes taking place at the surface S itself represent the exchange
of the system with the surroundings. These processes are
(i) mass fluxes penetrating the surface,
(ii)
work contributions by or on the system resulting from surface fo
rces, and
(iii) heat and radiative fluxes through the surface.
The amount of contained in the volume V is given by
(r,t) =
V
ψ(r, r
,t) dτ =
V
ρ(r, r
,t)ψ(r, r
,t) dτ (M6.60)
where r is the position vector from a suitable reference point to the volume V .The
vector r
is directed from the endpoint of r to the volume element dτ. Changes in
caused by the interaction of the system with the exterior will be denoted by d
e
/dt
while interior changes of will be written as d
i
/dt. The budget equation for
is then given by
d
dt
=
d
e
dt
+
d
i
dt
(M6.61)
The change with time d
e
/dt may be expressed by an integral over the surface S
bounding V :
d
e
dt
=−
S
F
ψ
(r, r
,t) · dS =−
V
∇·F
ψ
(r, r
,t) dτ (M6.62)
F
ψ
is a flux vector giving the amount of per unit surface area and unit time
streaming into V or out of it. The negative sign is chosen so that d
e
/dt is positive
when F
ψ
is directed into V . The conversion from the surface to the volume integral
is done with the help of the divergence theorem.
If Q
ψ
represents the production of per unit volume and time within V ,which
is also known as the source strength, then we may write
d
i
dt
=
V
Q
ψ
dτ (M6.63)
102 Integral operations
Q
ψ
is positive in cases of production of (sources) and negative in cases of
destruction (sinks).
Utilizing the budget operator (M6.57), the time differentiation of (M6.60) yields
d
dt
=
d
dt
V
ρψ dτ
=
V
D
3
Dt
(ρψ) dτ (M6.64)
Combination of (M6.61)–(M6.64) then results in the integral form of the budget
equation
V
D
3
Dt
(ρψ) dτ =
V
∂
∂t
(ρψ) +∇·(ρψv)
dτ =
V
−∇ · F
ψ
+ Q
ψ
dτ
(M6.65)
This expression describes the following physical processes.
(i) Local time change of :
V
∂
∂t
(ρψ) dτ
(ii) Convective flux of through S:
V
∇·(ρψv) dτ =
S
ρψv · dS
(iii) Nonconvective flux of through S: −
V
∇·F
ψ
dτ =−
S
F
ψ
· dS
(iv) Production or destruction of :
V
Q
ψ
dτ
Since equation (M6.65) is valid for an arbitrary volume V , we immediately obtain
the general differential form of the budget equation as
D
3
Dt
(ρψ) =
∂
∂t
(ρψ) +∇·(ρψv) =−∇·F
ψ
+ Q
ψ
(M6.66)
A very simple but extremely important example of a budget equation is the
continuity equation describing the conservation of mass of the material volume.
Identifying = M = constant in (M6.60), we have ψ = 1andQ
ψ
= 0since
mass cannot be created or destroyed. Furthermore, according to (M6.43) the total
mass flux through each surface element dS vanishes so that (M6.66) reduces to
D
3
ρ
Dt
=
∂ρ
∂t
+∇·(ρv) =
dρ
dt
+ ρ ∇·v = 0
(M6.67)
The continuity equation is a fundamental part of all prognostic meteorological
systems.
By expanding the budget operator and utilizing the continuity equation, we
obtain
D
3
Dt
(ρψ) = ψ
∂ρ
∂t
+∇·(ρv)
+ ρ
∂ψ
∂t
+ v ·∇ψ
= ρ
dψ
dt
(M6.68)

M6.6 The general form of the budget equation 103
This identity is called the interchange rule. Thus, the budget equation (M6.66) may
be written in the form
D
3
Dt
(ρψ) = ρ
dψ
dt
=−∇·F
ψ
+ Q
ψ
(M6.69)
Division of (M6.61) by the constant total mass M gives
dψ
dt
=
d
e
ψ
dt
+
d
i
ψ
dt
(M6.70)
Substitution of this equation into (M6.69) yields expressions for the external and
internal changes of ψ:
ρ
d
e
ψ
dt
=−∇·F
ψ
,ρ
d
i
ψ
dt
= Q
ψ
(M6.71)
These two equations are of great importance in thermodynamics.
It is worthwhile to reconsider equation (M6.69) using an argument due to Van
Mieghem (1973). Suppose we add the arbitrary vector X to F
ψ
so that ∇·X = β
and add β to the production term Q
ψ
on the right-hand side of this equation.
This mathematical operation does not change the budget equation in any way.
Consequently, there is no unique definition of either F
ψ
or Q
ψ
.
Finally we wish to give two applications of (M6.69) from thermodynamics that
will also be useful in our studies.
M6.6.1 The budget equation for the partial masses of atmospheric air
For meteorological applications discussed in this book we denote the partial masses
M
k
of atmospheric air in the following way: k = 0: dry air, k = 1: water vapor, k =
2: liquid water, and k = 3: ice. Hence the summation index N occurring in equations
(M6.40)–(M6.43) is restricted to N = 3. The index k appears sometimes as a
subscript and sometimes as a superscript. Liquid water and ice are treated as bulk
water phases; microphysical drop or ice-particle distributions are not considered in
this context.
Let ψ represent the mass concentration m
k
= M
k
/M. In this case the term F
ψ
represents the diffusion flux J
k
while the source term Q
ψ
is realized by the phase-
transition rate I
k
describing condensation and evaporation processes of liquid water
and ice. Thus (M6.69) assumes the form
D
3
Dt
(ρm
k
) = ρ
dm
k
dt
=−∇·J
k
+ I
k
(M6.72)
This is the budget equation for the mass concentrations. For dry air no phase
transitions are possible, so I
0
= 0. Moreover, since
3
k=0
m
k
= 1, it can be shown
that
3
k=0
I
k
= 0.

104 Integral operations
M6.6.2 The first law of thermodynamics
If ψ stands for the internal energy e, then equation (M6.69) represents a form of
the first law of thermodynamics. In this case we have F
ψ
= J
h
+ F
R
,whereJ
h
is
the heat flux (enthalpy flux) and F
R
is the radiative flux. The source term is given
by Q
ψ
=−p ∇·v + *,where* = J··∇v is the energy dissipation and J is the
viscous stress tensor. Hence we may write
D
3
Dt
(ρe) = ρ
de
dt
=−∇·(J
h
+ F
R
) − p ∇·v + *
(M6.73)
M6.7 Gauss’ theorem and the Dirac delta function
Let r, as usual, represent the position vector and apply the Gauss divergence
theorem to the function
r
r
3
=−∇
1
r
with r =
x
2
+ y
2
+ z
2
=
|
r
|
(M6.74)
The result is
V
∇·
r
r
3
dτ =
S
r
r
3
· dS = 0
since ∇·
r
r
3
=
3
r
3
+ r · e
r
∂
∂r
1
r
3
= 0
(M6.75)
provided that r differs from zero at all points on and within the surface S.This
means that (M6.75) is valid only if the origin from which r is drawn does not lie
within the volume V or on its boundary. Since the divergence theorem requires
that the functions to which it is applied have continuous first partial derivatives
throughout the volume of integration, it cannot be applied to r/r
3
if the origin
of r is within S. To handle this situation, we modify the region of integration by
constructing a sphere of radius * having the origin as its center; see Figure M6.11.
Within the region V
between S and S
the function r/r
3
satisfies the condition
of the divergence theorem so that (M6.75) is valid, so that
S
r
r
3
· dS +
S
r
r
3
· dS = 0(M6.76)
According to Figure M6.11, in the last integral of (M6.76) we may make the
replacements r = *, r =−*n so that r · dS =−*n · n dS
=−*dS
and we
obtain
S
r
r
3
· dS =
1
*
2
S
dS
= 4π (M6.77)

M6.7 Gauss’ theorem and the Dirac delta function 105
Fig. M6.11 Exclusion of a singular point from a three-dimensional region by an auxiliary
spherical surface S
.
If S is a closed regular two-sided surface, then combining (M6.75) and (M6.77)
yields
S
r
r
3
· dS =
4π if O is inside S
0ifO is outside S
(M6.78)
This is known as Gauss’ theorem. We refer to Wylie (1966), where further details
may be found.
The one-dimensional Dirac delta function has the properties that
δ(x − a) = 0forx = a
x
δ(x − a) dx =
1ifa ∈ x
0ifa/∈ x
x
f (x)δ(x − a) dx = f (a)
(M6.79)
where f (x) is any well-behaved function and a is included in the region of inte-
gration. Generalizing, we have
δ(r − r
) = 0ifr = r
δ(r − r
) = δ(r
− r) = δ(x − x
)δ(y − y
)δ(z − z
)
V
δ(r − r
) dτ =
1ifr
∈ V
0ifr
/∈ V
V
f (r)δ(r − r
) dτ =
f (r
) if r
∈ V
0ifr
/∈ V
(M6.80)
An excellent reference, for example, is Arfken (1970).
106 Integral operations
M6.8 Solution of Poisson’s differential equation
One of the most important differential equations in mathematical physics is Pois-
son’s equation,
∇
2
φ = Cf (r) (M6.81)
with C = constant and where f (r) is some function to be specified later. We will
show that this equation is satisfied by the integral
φ(r) =−
C
4π
V
f (r
)
|
r − r
|
dτ
(M6.82)
To verify the validity of this integral we substitute (M6.82) into (M6.81) and carry
out the differentiation with respect to r. Formally we may write
∇
2
φ(r) =−
C
4π
V
f (r
) ∇
2
1
|
r − r
|
dτ
(M6.83)
It is convenient and permissible to translate the origin to r
and consider
∇
2
|
1/r
|
=∇
2
(1/r). Now we have exactly the situation leading to the devel-
opment of Gauss’ theorem (M6.78). Using this theorem together with (M6.74) and
(M6.75), we obtain
−
V
∇
2
1
r
dτ =
V
∇·
r
r
3
dτ =
4π if the origin of r ∈ V
0 if the origin of r /∈ V
(M6.84)
This may be conveniently expressed by means of the Dirac delta function as
∇
2
1
r
=−4πδ(r − 0) (M6.85)
We must modify (M6.85) since we have displaced the origin to r
.Theterm4π in
Gauss’ theorem appears if and only if the volume includes the point r
. Therefore,
we replace (M6.85) by
∇
2
1
|
r − r
|
=−4πδ(r − r
) with r
= 0(M6.86)
Substitution of (M6.86) into (M6.83) leads to the original differential equation
(M6.81)
∇
2
φ(r) =−
C
4π
V
f (r
)
−4πδ(r − r
)
dτ
= Cf (r) (M6.87)
M6.9 Appendix: Remarks on Euclidian and Riemannian spaces 107
M6.9 Appendix: Remarks on Euclidian and Riemannian spaces
A point in a generalized n-dimensional space is specified by the coordinates
q
1
,q
2
,..., q
n
. The coordinates of any two neighboring points in this space differ
by the differentials dq
1
,dq
2
,..., dq
n
. One speaks of a Riemannian space if the
distance between these two points is defined by the metric fundamental form
dr
2
= g
mn
dq
m
dq
n
(M6.88)
If it is possible to transform the entire space so that dr
2
can be expressed by the
Cartesian coordinates x
1
,x
2
,..., x
n
with
dr
2
= δ
mn
dx
m
dx
n
(M6.89)
then the space is called a Euclidian space. For the common three-dimensional
Euclidian space we may write
dr
2
= dx
2
+ dy
2
+ dz
2
(M6.90)
The basic difference between the Riemannian and the Euclidian space is that
the Euclidian space is considered flat whereas the Riemannian space is curved.
A curved surface embedded in a three-dimensional Euclidian space is the only
Riemannian space which is perceptible to us. In general, the transformation from
(M6.88) to the form (M6.89) is not possible.
The metric fundamental quantities of a certain space contain all the required
information that is necessary in order to find out whether we are dealing with a
flat or a curved space. If it turns out that the g
ij
are constant then the space is
flat. Necessarily, in a curved space the g
ij
are not constants, but depend on the
coordinates q
i
. However, from the simple fact that the g
ij
are functions of the
coordinates q
i
it cannot be concluded that the space is curved. For example, let us
consider polar coordinates, in which the distance in space is defined by the metric
fundamental form
dr
2
= dr
2
+ r
2
dα
2
with g
11
= 1,g
22
= r
2
(M6.91)
so that one of the g
ij
is a function of the generalized coordinate q
2
= r.Weleave
it to the reader to show that (M6.91) can be transformed into the Cartesian form
(M6.89). In this particular case it is quite obvious that the space is flat. Another
example is provided by constructing on a plane sheet of paper a Cartesian grid.
Rolling the paper to form a cylinder of radius R does not change the distances on
the surface, showing that it is possible to transform the fundamental form
dr
2
= dR
2
+ R
2
dα
2
+ dz
2
with g
11
= 1,g
22
= R
2
,g
33
= 1(M6.92)
108 Integral operations
into the Cartesian form (M6.89). A very inportant curved space is the surface of a
sphere, which is characterized by the radius r, the latitude ϕ, the longitude λ,and
the metric fundamental form
dr
2
= r
2
cos
2
ϕdλ
2
+ r
2
dϕ
2
+ dr
2
with g
11
= r
2
cos
2
ϕ, g
22
= r
2
,g
33
= 1
(M6.93)
By inspection or trial-and-error analysis it is very difficult to determine whether
a given coordinate-dependent metric tensor g
ij
(q
k
) can be transformed into Carte-
sian coordinates. Fortunately, there is a systematic method to determine whether
the space is flat or curved by calculating the Riemann–Christoffel tensor or the
curvature tensor.
Let us consider the expression (∇
i
∇
j
−∇
j
∇
i
)A
k
,where∇
i
is the covariant
derivative. By using the methods we have studied previously, omitting details, we
can show that
∇
i
(∇
j
A
k
) −∇
j
(∇
i
A
k
) = A
n
R
n
kij
with R
l
kij
=
m
ki
l
mj
−
∂
∂q
i
l
kj
−
m
kj
l
mi
+
∂
∂q
j
l
ki
(M6.94)
If the curvature tensor R
l
kij
= 0 then the space is flat or uncurved. If R
l
kij
= 0then
the space is curved as in the case of a spherical surface. This fact shows that no
Cartesian coordinates exist for the sphere.
In atmospheric dynamics we often simplify the metric tensor by assuming that
the radius extending from the center of the earth does not change with height
throughout the meteorologically relevant part of the atmosphere. The simplification
applies only to those terms of dr
2
for which the radius appears in undifferentiated
form. This type of Riemannian space is no longer perceptible to us.
Let us briefly consider the parallel transport of a vector since this concept can
be used to determine the curvature tensor. By definition, a vector is transported
parallelly if its direction and length do not change. Thus in the plane or, more
generally, in the Euclidian space the parallel transport does not change the vector.
The reason for this is that the basis vectors of the Euclidian space are constant and
do not have to be differentiated whenever the vector is differentiated. The parallel
displacement of a vector can be used to define the Euclidian space. For such a space
the pararallel displacement along an arbitrary closed curve transports the vector to
its original position without changing its length and direction.
As an illustration we consider polar coordinates as shown in Figure M6.12. In
this two-dimensional space we transport the vector parallelly from point P to Q.
While the vector itself remains constant the components (x = r cos α, y = r sin α)
of the vector change. If we transport the vector around the circle back to P we
obtain the original vector.
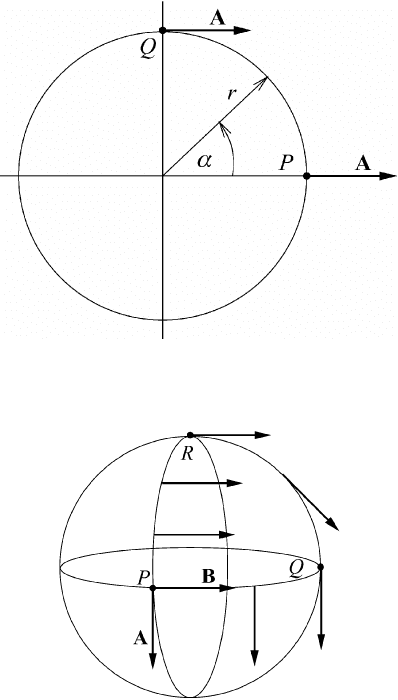
M6.9 Appendix: Remarks on Euclidian and Riemannian spaces 109
Fig. M6.12 Parallel transport of a vector in the two-dimensional Euclidian space.
Fig. M6.13 The path dependence of surface parallelism.
A different situation occurs if the vector is transported along a curved surface
since surface parallelism depends on the path. The definition “parallel transport
of the surface vectors” implies two operations, namely a parallel shift in space,
followed by a projection onto the tangent plane. We will demonstrate this situation
in Figure M6.13 for a sphere. Let us transport the vector A along a great circle from
point P to Q. Both points are located on the equator. From point Q the vector is
displaced to the pole, point R, and then back to point P . During the transport the
angle between the vector and the great circles (geodesic circles) remains constant.
The displacement of the vector along the closed path results in a vector B,which
is perpendicular to the original vector A. Thus surface parallelism depends on the
path. Had we transported A from P to Q and then back to P , of course, we would
have obtained the original vector.

110 Integral operations
M6.10 Problems
M6.1: Show that the integral
S
dS = 0.
M6.2: In equation (M6.49) set A = (1/ρ) ∇p to verify the following statement:
d
dt
L(t)
dr·
1
ρ
∇p
=
L(t)
(d
g
p)
d
dt
1
ρ
− (d
g
ρ)
dp
dt
where ρ and p are scalar field functions.
M6.3: Use the integral theorems to verify the following statements:
∇×
dv
dt
=
d
dt
(∇×v) + (∇×v) ∇·v − (∇×v) ·∇v
∇·
dv
dt
=
d
dt
(∇·v) +∇v ··∇ v
M6.4: Consider the vector field A = A
x
(x,y)i + A
y
(x,y)j in the (x,y)-plane.
(a) Find the closed line integral
dr ×A. The closed line is a rectangle defined
by the corner points (0, 0), (L, 0), (L, M), (0,M).
(b) Apply the result of (a) to the following situation:
A
x
(x = 0,y) = cos y, A
x
(x = L, y) = sin y
A
y
(x,y = 0) = x, A
y
(x,y = M) =−1/L
M6.5: The vector field A = Cr/r, with C = constant and r =
|
r
|
,isgiven.
(a) Calculate the line integral
(2)
(1)
dr · A for an arbitrary path from (1) → (2).
(b) Calculate the surface integral
S
dS ·A for a spherical surface of radius a about
the origin.
M6.6: For the vector field v
6
= Ω × r, Ω = constant, calculate the line integral
v
6
· dr
(a) for a circle of radius a about the axis of rotation, and
(b) for an arbitrary closed curve.
Use Stokes’ integral theorem.
M6.7: Show that
V
∇ψ ·∇×(A ·∇A) dτ = 0
On the surface of the volume the vector A is of the form A = B × n,wheren is
the unit vector normal to the surface. In addition to this, assume that A ·∇ψ = 0,
where ψ is a scalar field function. Hint: Use Lamb’s transformation (M3.75).
