Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

Part 2

Dynamics of the atmosphere

The laws of atmospheric motion

1.1 The equation of absolute motion

The foundation to all of atmospheric dynamics is the description of motion in the

absolute reference frame. This is a Cartesian coordinate system that is ﬁxed with

respect to the “ﬁxed” stars. For all practical purposes we may regard this system as

an inertial coordinate system for an earthbound observer. In this reference frame

we may apply Newton’s second law of motion stating that the change of momentum

M with time of an arbitrary body equals the sum of the real forces acting on the

body. Real forces must be distinguished from ﬁctitious forces, which are not due

to interactions of a particle with other bodies. Fictitious forces result from the

particular type of the coordinate system which is used to describe the motion of

the particle.

For a volume V (t) in the absolute frame we may then write



V (t)

ρv

dτ =



(1.1)

where dτ is a volume element, ρ is the density of the medium, and v

is the absolute

velocity. The forces appearing on the right-hand side of this equation include mass

or volume forces F

and surface forces P

of the system. We do not need to include

molecular-type forces between mass elements occurring in the interior part of the

system since their net effect adds up to zero. If the f

represent the forces per unit

mass and p

the surface forces per unit surface area, we may write





V (t)



ρf

dτ,





S(t)



dS (1.2)

Here, S(t) is the surface enclosing the volume V (t)anddS is a surface element.

Combination of these two formulas gives



V (t)

ρv

dτ =



V (t)

(ρv

) dτ =



V (t)



ρf

dτ +



S(t)



dS (1.3)

133

134 The laws of atmospheric motion

The left-hand side of this equation refers to the rate of change with time of a ﬂuid

volume whose surface elements move with the respective absolute velocity v

.The

budget operator D

/Dt is given by (M6.58). In the following the index 3 will be

omitted for brevity.

The only mass force we need to consider is the gravitational attraction of the

earth. We are not going to deal with tidal forces so that we are justiﬁed in ignoring

the gravitational pull resulting from celestial bodies. To keep things simple, we

consider the entire mass of the earth M

to be concentrated at its center. According

to Newton’s law of attraction,thegravitational force f

= f

acting on unit mass is

given by

=−

γM

=−

γM

r (1.4)

where γ is the gravitational constant and r = rr

the position vector extending

from the center of the earth to the ﬂuid volume element of unit mass. The force f

may also be expressed in terms of a potential. To recognize this, we take the curl

of f

and obtain

∇×f

=−γM



∇×r −

× r



= 0(1.5)

By the rules of vector analysis, f

may now be replaced by the gradient of a scalar

function,

=−∇φ

,φ

=−

γM

+ constant (1.6)

The minus sign is conventional. The term φ

is called the gravitational potential.

We will subsequently assume that φ

depends on position only and not on time so

that

= φ

(r),



∂φ

∂t



= 0(1.7)

Next, we consider the surface forces acting on a surface element. These result

from the pressure force p

=−pn acting in the opposite direction −n of dS,and

from the normal and tangential viscous forces p

= n ·J which depend on the state

of motion of the medium. The quantity J is known as the viscous stress tensor,

which is assumed to be symmetric. At this point the stress tensor is introduced only

formally, but it will be discussed in more detail in Chapter 5. The surface forces

are then given by



dS = n dS · (−pE + J) = dS · (−pE + J)(1.8)

where

E is the unit dyadic.

1.1 The equation of absolute motion 135

Substituting (1.8) and (1.6) into (1.3) we obtain



V (t)



(ρv

) + ρ ∇φ



dτ +



S(t)

dS · (pE − J) = 0(1.9)

Application of Gauss’ divergence theorem (M6.31) and use of the interchange rule

(M6.68) gives



V (t)



+ ρ ∇φ

+∇p −∇·J



dτ = 0(1.10)

Since the volume of integration is completely arbitrary, we obtain the differential

form

=−ρ ∇φ

−∇p +∇·J

(1.11)

This important equation is known as the equation of absolute motion. It is funda-

mental to all of atmospheric dynamics.

In order to formulate the last term of (1.11) we use the following analytic

expression for the stress tensor

J = µ(∇v

+ v



∇) −λ ∇·v

E,λ=

µ − l

(1.12)

A detailed derivation of this equation may be found, for example, in TH. In (1.12)

we have neglected the effects of transitions between the different phases of water

on the stress tensor. We have also used Lam

e’s coefﬁcients of viscosity λ and µ,

which will be treated as constants. Substitution of (1.12) into (1.11) results in the

famous Navier–Stokes equation

=−ρ ∇φ

−∇p + µ ∇

+ (µ − λ) ∇(∇·v

)

(1.13)

If we ignore the last two terms involving Lam

e’s viscosity coefﬁcients then we

obtain the Euler equation

=−ρ ∇φ

−∇p

(1.14)

136 The laws of atmospheric motion

1.2 The energy budget in the absolute reference system

In the absolute reference system the attractive potential represents the potential

energy of unit mass. Application of the budget operator yields

(ρφ

) = ρ

dφ

= ρ

∂φ

∂t

+ ρv

·∇φ

(1.15)

Owing to the condition of stationarity (1.7) the budget equation for the gravitational

attraction reduces to

(ρφ

) = ρv

·∇φ

(1.16)

Next we need to derive the budget equation for the kinetic energy K

= ρv

/2in

the absolute reference frame. Scalar multiplication of (1.11) by v

and application

of the identities

∇·(v

· J) = J··∇v

+ v

· (∇·J)

∇·(pv

) = p ∇·v

+ v

·∇p =∇·(pv

· E)

(1.17)

yields the desired budget equation





+∇·[v

· (pE − J)] =−ρv

·∇φ

+ p ∇·v

− J··∇v

(1.18)

Equations (1.16) and (1.18), together with the budget equation for the internal

energy e (M6.73), constitute the energy budget for the absolute system:

(ρφ

) = ρv

·∇φ





+∇·[v

· (pE − J)] =−ρv

·∇φ

+ p ∇·v

− J··∇v

(ρe) +∇·(J

+ F

) =−p ∇·v

+ J··∇v

(1.19)

The term J

occurring in the budget equation for e describes the sensible heat

ﬂux and F

is the radiative ﬂux. This equation is derived in various textbook on

thermodynamics; see for example TH.

It can be seen that the sum of the source terms on the right-hand side of (1.19)

of the entire system vanishes. This simply means that energy is transformed and

exchanged between various parts of the system, but it is neither created nor de-

stroyed. In other words, each source occurring in one equation is compensated by

a sink (minus sign) in one of the other equations.

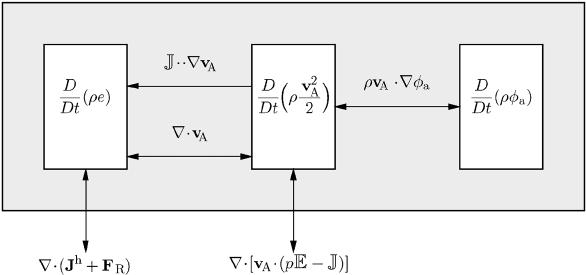
1.3 The geographical coordinate system 137

Fig. 1.1 The energy-ﬂux diagram in the absolute reference frame.

For visual purposes it is customary to arrange the energy ﬂuxes (1.19) in the

form of a circuit diagram as shown in Figure 1.1. The expressions above the arrows

between the three energy boxes describe the energy transitions. These transitions

may have either a positive or a negative sign with the exception of the positive

deﬁnite energy dissipation

J ··∇v

which ﬂows in one direction only. This term

is also known as the Rayleigh dissipation function. The arrows connecting the

system with its surroundings are the divergence terms of the budget equations. If

the system is closed energetically then all divergence terms vanish. In this case the

total energy 

= (

+ v

/2 + e) is conserved.

1.3 The geographical coordinate system

All meteorological observations are performed on the rotating earth. Therefore, our

goal must be to describe the motion of the air from the point of view of an observer

participating in the rotational motion. Any motion viewed from a station on the

rotating earth is known as relative motion. Since the equation of absolute motion

(1.13) refers to an inertial system, we must ﬁnd a relation between the accelerations

of absolute and relative motion.

Let us consider a rotating coordinate system whose origin is placed at the earth’s

center. The vertical axis of this system coincides with the earth’s axis so that the

coordinate system is rotating with the constant angular velocity Ω of the earth

from west to east. Moreover, we assume that the center of the earth and the center

of the inertial coordinate system coincide and that the vertical axis of the inertial

system is also along the rotational axis of the earth and is pointing to the pole-star.

If a point P in this rotating coordinate system remains ﬁxed in the sense that its

longitude λ, latitude ϕ, and the distance r extending from the center of the earth to

the point do not change with time, we speak of rigid rotation and a rigidly rotating

coordinate system. This situation is depicted in Figure 1.2.

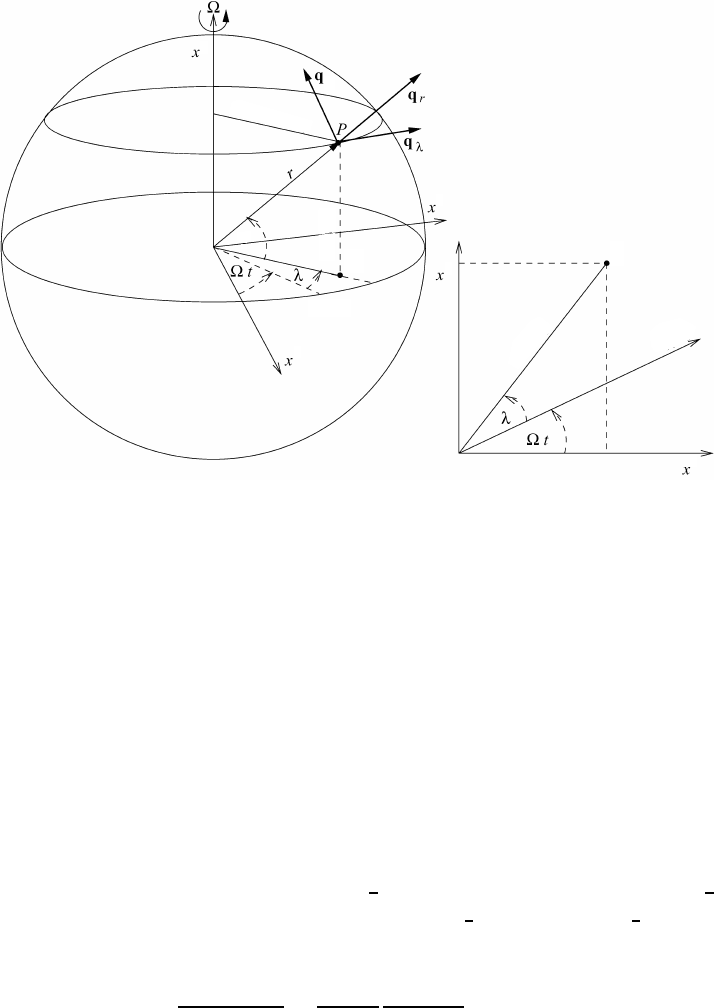
138 The laws of atmospheric motion

R = r cos ϕ

r sin ϕ

λ = 0

r cos ϕ

λ = 0

Fig. 1.2 The geographical coordinate system with generalized coordinates q

= λ, ϕ, r

representing the longitude λ, the latitude ϕ, and the distance r of a point P .Alsoshown

are t

he corresponding basis vectors

, q

. The axes x

and x

of the inertial system

lie in the equatorial plane of

the earth.

We can see immediately that the rotational velocity v



of this point is directed

along the basis vector q

and is given by



= Ω × r (1.20)

The formal derivation of (1.20) will be given later. The angular velocity Ω is

determined by the period of rotation of the earth with respect to the ﬁxed stars.

This period of rotation is called the sidereal day (sidereal is an adjective derived

from the Latin word for star). Since the earth moves around the sun, the sidereal

day differs in length from the solar day which is the period of rotation with respect

to the sun. In one year the earth rotates 365

times with respect to the sun, but 366

times with respect to the stars so that one year = 365

solar days = 366

sidereal

days. Therefore, we have

Ω

=  =

2π

sidereal day

366.25

365.25

2π

solar day

= 7.292 × 10

−5

−1

(1.21)

In our later studies it will be of advantage to introduce pressure or some other

suitable variable of state as the vertical coordinate instead of height in order to

1.3 The geographical coordinate system 139

effectively describe the motion of the air. Let us consider, for example, a point

of ﬁxed longitude and latitude on a pressure surface. Owing to heating processes,

pressure surfaces will deform so that this point will experience a change in height

with respect to the ground and, therefore, with respect to the center of the absolute

coordinate system. Of course, this displacement is extremely small relative to the

total distance from the center of the earth to the point. The vertical motion of the

point, however, cannot be ignored in all situations. Summing it up, this point is not

only moving with the rotational velocity of the earth, but also participating in the

deformational motion of the pressure surface. This deformation velocity v

must be

added to v



to give the velocity of the point v

with respect to the absolute system,

= v



+ v

(1.22)

As the next step in our investigation it will be necessary to represent the individual

time derivative both in the absolute and in the relative coordinate systems. The

individual time derivative itself describes the change of an air parcel in such a way

that it is independent of any coordinate system. Therefore, the individual derivative

d/dt is called an invariant operator. However, the constituent parts of this operator

depend on the coordinate system used to describe the motion and, therefore, they

are not invariants. A detailed derivation of the individual time derivative is given

in Section M4.2.

It will be recalled that, in general curvilinear coordinates, the position vector is

deﬁned only inﬁnitesimally. Exceptions are curvilinear systems for which ∂e

/∂r =

0. An example of this exception is the geographical coordinate system. It should

be recalled that, in rotating coordinate systems, the basis vectors are functions of

time also. The position vector r in the Cartesian system may also be expressed in

terms of the generalized coordinates q

using the transformation x

= x

,t).

Thus, we may write

r = x

, r = r(q

,t)(1.23)

In the absolute system we use Cartesian coordinates to represent dr/dt, whereas

for the relative system we are going to employ contravariant measure numbers.

Application of the invariant operator d/dt to the position vector in the two coordi-

nate systems then gives

system:



∂r

∂t



∂r

∂x



∂x

∂t



+ ˙x

= ˙x

= v

system:



∂r

∂t



∂r

∂q



∂r

∂t



+ ˙q

with

∂r

∂x

= i

∂r

∂q

= q

(1.24)

140 The laws of atmospheric motion

In the absolute or the Cartesian system the individual derivative of the position

vector is equivalent to the absolute velocity. The local time derivative vanishes

since x

is held constant. In the relative system the partial derivative of r with

respect to time, holding q

constant, describes the velocity v

of the point P as

registered in the absolute system. The components of v

in the absolute or inertial

system are denoted by W

. The vector v describes the velocity of a parcel of air

relative to the earth. Therefore, we have

v = ˙q

, v



∂r

∂t





∂x

∂t



= W

(1.25)

From (1.24) and (1.25) we now obtain

= v

+ v

(1.26)

which is known as the addition theorem of the velocities, see also Section M4.2.

Hence, the absolute velocity v

of a parcel of air is the sum of the velocity v

the point relative to the absolute system plus the relative velocity of the parcel at

the point as registered in the moving system. Taking the individual time derivative

of (1.26) results in the relation between the accelerations of absolute and relative

motion, as was mentioned at the beginning of this section.

1.3.1 Operations involving the rotational velocity v



In this section we will present some important relations that will be useful for our

later studies.

1.3.1.1 The divergence of v



in the geographical coordinate system

We will now introduce the coordinates of the geographical system spoken of with

the help of Figure 1.2. This system is performing a rigid rotation so that v

= 0.

The system is rotating with constant angular velocity about the x

-axis so that

Ω = i

 (1.27)

We wish to specify the coordinates of the point P whose projection onto the

equatorial plane is denoted by P



. During time t, the longitude λ = 0 passing

through Greenwich moves the angular distance t as measured from the x

-axis of

the absolute system. The angular distance of the point P



then is given by t + λ

so that the coordinates of the point P in the absolute system may be expressed in