Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

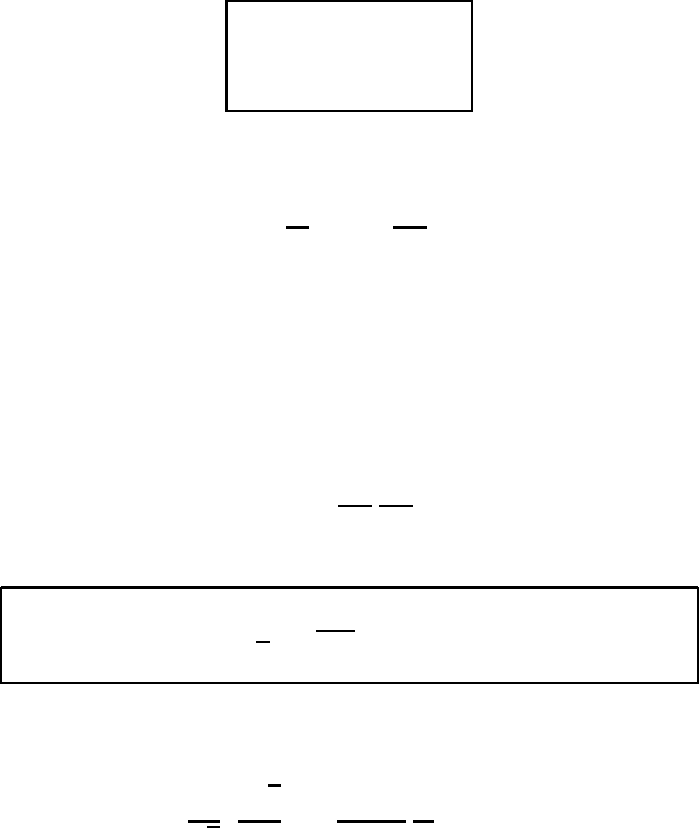
1.3 The geographical coordinate system 141

terms of the geographical coordinates (λ, ϕ, r) by means of

= r cos ϕ cos(λ + t)

= r cos ϕ sin(λ + t)

= r sin ϕ

(1.28)

We now apply (1.25) to ﬁnd the rotational velocity v



. In the present situation

= 0sothat

= v





∂r

∂t



= i



∂x

∂t



= W

=−x

+ x

= Ω × r

with W

= W

=−x

= W

= x

(1.29)

This veriﬁes the validity of (1.20). Recall that in the Cartesian system there is no

difference between covariant and contravariant coordinates.

We now wish to ﬁnd the metric fundamental quantities g

of the orthogonal

geographical coordinate system. For such a system we may apply the relation

(M3.15):

∂x

∂q

∂x

∂q

(1.30)

On substituting (1.28) into this expression, after a few easy steps we ﬁnd

= r

cos

ϕ, g

= r

= 1,g

= 0fori = j =⇒

√





= r

cos ϕ

(1.31)

The divergence of the velocity of the point v

= v



is expressed by the general

relation (M4.36)

∇·v

√





∂

√

∂t





cos ϕ

∂

∂t



cos ϕ



λ,ϕ,r

= 0(1.32)

Since the coordinates ϕ and r are held constant in the time differentiation, it is

found that the divergence of v



in the rigidly rotating geographical system is

zero, as expected. If the deformation velocity differs from zero, we ﬁnd that the

divergence of v

does not vanish. This situation will be treated later. The validity

of (1.32) can also be veriﬁed by using the deﬁnition (1.20), i.e.

∇·v



=∇·(Ω × r) =−Ω · (∇×r) = 0(1.33)

142 The laws of atmospheric motion

1.3.1.2 Rotation and the vector gradient of v



Using the Grassmann rule (M1.44) we ﬁnd immediately

∇×v



=∇×(Ω × r) = (∇·r)Ω − Ω · (∇r) = 3Ω − Ω · E = 2Ω

(1.34)

showing that the rotation of v



is a constant vector whose direction is parallel to

the rotational axis of the earth.

We will now take the gradient of v



. Recalling that ∇r = E is a symmetric

tensor, that is ∇r = r



∇, we ﬁnd immediately

∇v



=∇(Ω × r) =−∇(r × Ω ) =−E × Ω =−Ω × E





∇=(Ω × r)



∇=Ω × E =−∇v



(1.35)

where use of (M2.67) has been made. Therefore, the gradient of v



is an anti-

symmetric tensor. By taking the scalar product of an arbitrary vector A with the

gradient of v



, we obtain the very useful expressions

A ·∇v



=−A · (E × Ω) = Ω × A

∇v



· A =−(Ω × E) ·A = A × Ω

(1.36)

If A represents the velocities v



and v we ﬁnd

(a) v



·∇v



= Ω × v



= Ω × (Ω × r)

(b) v ·∇v



= Ω × v

(1.37)

These expressions will be needed later.

1.3.2 The centrifugal potential

For meteorological purposes the rotational vector of the earth may be treated as a

constant vector. On applying the Grassmann rule to the curl of the vector product

Ω × v



we ﬁnd with the help of (1.33) and (1.36)

∇×(Ω × v



) = (∇·v



)Ω − Ω ·∇v



= 0(1.38)

From vector analysis we know that an arbitrary vector whose curl is vanishing can

be replaced by the gradient of a scalar ﬁeld function. Therefore, we may write

∇φ

= Ω × v



(1.39)

Since we are dealing with a rotating coordinate system, it is customary to call the

scalar ﬁeld function φ

the centrifugal potential, which will be determined soon.

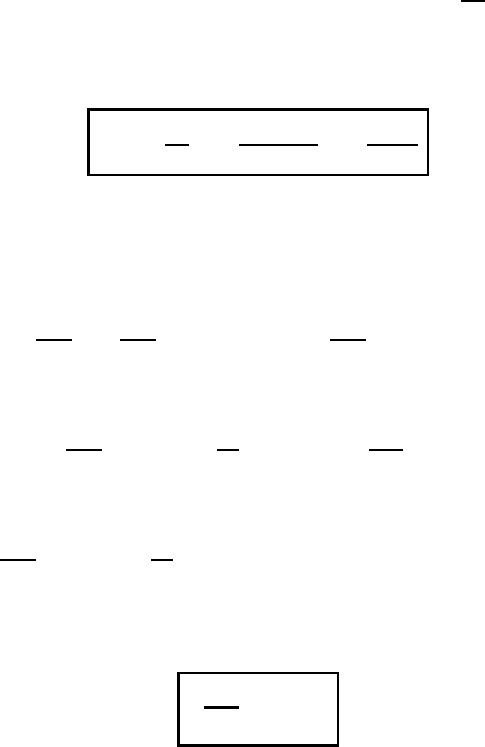
1.3 The geographical coordinate system 143

By taking the scalar product of v



and ∇φ

we ﬁnd that the angle between these

two vectors is 90

◦



·∇φ

= v



· (Ω × v



) = 0(1.40)

Owing to the gravitational attraction, equipotential surfaces φ

= constant are of

spherical shape. Therefore, we must also have



·∇φ

= 0(1.41)

showing that v



and ∇φ

are also orthogonal to each other. This may also be easily

veriﬁed with the help of (1.20).

In order to ﬁnd the centrifugal potential itself, we apply (1.37) to (1.39) and

utilize the fact that the tensor ∇v



is antisymmetric. Thus we obtain

∇φ

= Ω × v



= v



·∇v



=−v



· v





∇=−∇







(1.42)

By comparison we ﬁnd, to within an abitrary additive constant, which we set equal

to zero, the required expression for the centrifugal potential:

=−



=−

(Ω × r)

=−



(1.43)

R is the distance from the point under consideration to the earth’s axis; see

Figure 1.2.

Finally, the invariant individual time derivative of v



can be written either in the

absolute or in the relative system:





∂v



∂t



+ v

·∇v





∂v



∂t



+ v ·∇v



(1.44)

In the Cartesian system the local time derivative of v



vanishes because



∂v



∂t



= Ω ×



∂r

∂t



= Ω × i



∂x

∂t



= 0(1.45)

In the general q

system we obain



∂v



∂t



= Ω ×



∂r

∂t



= Ω × (v



+ v

) =∇φ

+ Ω × v

(1.46)

where we have used (1.25) and (1.39). For the rigidly rotating coordinate system

with v

= 0 this expression reduces to



∂v



∂t



=∇φ

(1.47)

144 The laws of atmospheric motion

1.3.3 The budget operator

Before we apply the budget operator to the velocity v of the rigidly rotating system,

we will give a general expression for an abitrary system including deformation. We

refer to Section M6.5. According to (M6.66), omitting the index 3 for brevity, the

budget operator is given by

(ρψ) =

∂

∂t

(ρψ)

+∇·(ρψ v

)

∂

∂t

(ρψ)

+ v

·∇(ρψ) + ρψ ∇·v

(ρψ) + ρψ ∇·v + ρψ ∇·v

(1.48)

since v

= v + v



+ v

and ∇·v



= 0. Now we write the total time derivative in

the q

-coordinate system and ﬁnd

(ρψ) =

∂

∂t

(ρψ)

+∇·(ρvψ) +ρψ ∇·v

(1.49)

Setting in (1.48) ψ = 1 yields the general form of the continuity equation:

dρ

+ ρ ∇·v + ρ ∇·v

= 0

(1.50)

If the deformation velocity v

is zero, (1.50) reduces to the continuity equation for

the rigidly rotating coordinate system.

Before we derive the equation of motion for the relative system, we will intro-

duce a special notation to avoid notational ambiguities. Suppose that we wish to

differentiate locally the vector A = A

with respect to time, yielding



∂A

∂t





∂A

∂t



+ A



∂q

∂t



(1.51)

The ﬁrst part of the product differentiation on the right-hand side of (1.51) describes

the differentiation of the measure numbers A

with the basis vector q

held constant.

It might be more convenient to put the vector A itself into the ﬁrst operator on the

right-hand side instead of its measure numbers. This can be done quite validly

since q

is held constant. However, in order to avoid an ambiguity in our notation,

we place a vertical line



on the local time-derivative operator to indicate that

is not to be differentiated with respect to time. Thus, the following notation is

introduced:

∂A

∂t





∂A

∂t



(1.52)

1.3 The geographical coordinate system 145

The second part of the time differentiation in (1.51) involves the basis vector itself:



∂q

∂t



∂

∂t



∂r

∂q



∂

∂q



∂r

∂t



∂v

∂q

(1.53)

where we have substituted the velocity v

as deﬁned in (1.25). The local time

derivative of A is then given by



∂A

∂t



∂A

∂t



∂v

∂q

∂A

∂t



·q

∂v

∂q

∂A

∂t



+A ·∇v

(1.54)

With this expression we obtain for the individual time derivative of A



+ A ·∇v

with



∂A

∂t



+ v ·∇A

(1.55)

While the vertical line excludes the differentiation of the basis vector q

with

respect to time, it does not exclude the differentiation with respect to the spatial

coordinates. Moreover, it should be clearly recognized that the time dependency of

the basis vectors is not lost by any means since it is included in the gradient of v

We proceed similarly with the budget operator. Application of (1.48) to the

vector A results in

(ρA) =

(ρA)



+ ρA ·∇v

with

(ρA)



= ρ



∂

∂t

(ρA)



+∇·(ρvA) + ρA ∇·v

(1.56)

We would like to point out that equations (1.54)–(1.56) are general and include the

deformation velocity.

In the special case of rigid rotation, the deformation velocity is zero so that (1.36)

may be applied. Whenever the expression A ·∇v

appears it may then be replaced

A ·∇v

= A ·∇v



= Ω × A for v

= 0(1.57)

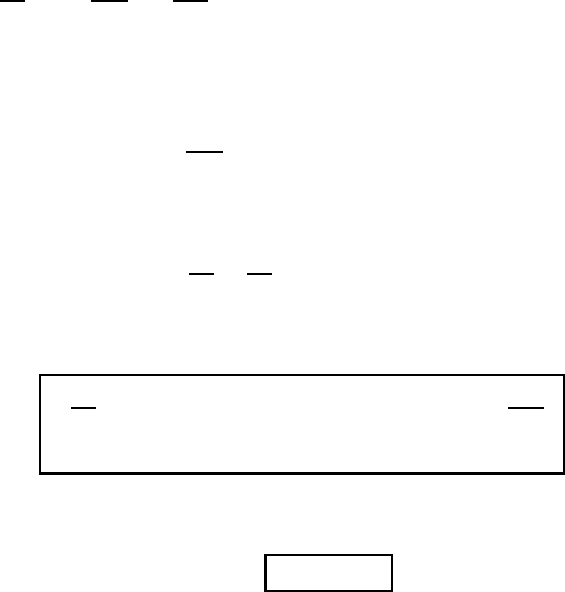
146 The laws of atmospheric motion

1.4 The equation of relative motion

The starting point of the derivation is the equation of absolute motion (1.13).

Introducing the addition theorem (1.26), (1.13) may be written as

=−ρ



−ρ

−ρ ∇φ

−∇p +µ ∇

+(µ −λ) ∇(∇·v

)(1.58)

We now replace two of the individual derivatives. Application of (1.46) to (1.44)

and using (1.37b) gives



=∇φ

+ Ω × v

+ Ω × v (1.59a)

With the help of (1.55) and (1.37b) we obtain



+ Ω × v + v ·∇v

(1.59b)

Substitution of (1.59a) and (1.59b) into (1.58) gives the equation of relative motion:



=−2ρΩ × v − ρΩ × v

− ρv ·∇v

− ρ

− ρ ∇φ −∇p + µ ∇

+ (µ − λ) ∇(∇·v

)

(1.60)

where the centrifugal and the attractive potential have been combined to give the

geopotential,thatis

φ = φ

+ φ

(1.61)

From (1.6) we know that surfaces of constant gravitational potential are spherical

surfaces. The gravitational potential increases with increasing distance from the

center of the earth so that −∇φ

is pointing toward the center of the earth. According

to (1.43) the centrifugal potential φ

= constant is represented by cylindrical

surfaces whose negative gradient −∇ φ

is pointing away from the earth’s axis.

Owing to the rotational symmetry, the two surfaces may be easily added graphically

in a cross-section containing the earth’s axis. The resulting surfaces of geopotential

φ = constant are shown in Figure 1.3.

Near the earth’s surface, i.e. in the part of the atmosphere relevant to weather,

surfaces of constant geopotential may be viewed as rotational ellipsoids. In most

of our studies we will even assume that the ellipsoidal surfaces may be replaced

by spherical surfaces. Moreover, we assume that the geopotential is a function of

position only and set ∂φ/∂t = 0.

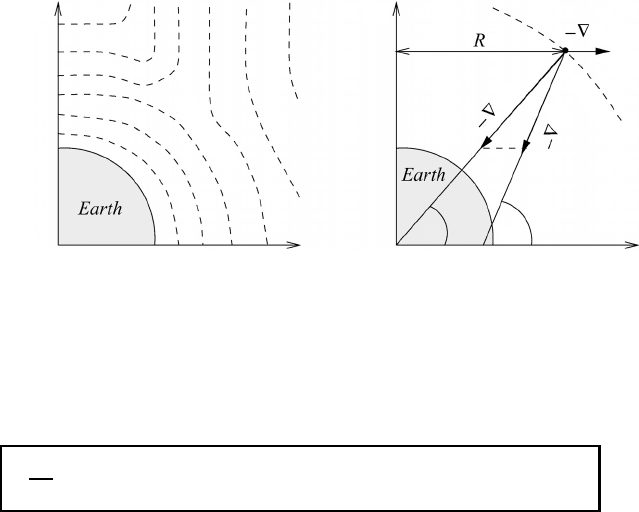
1.5 The energy budget of the general relative system 147

φ = constant

(b)(a)

Fig. 1.3 (a) A cross-section of geopotential surfaces. (b) Directions of the negative gradi-

ents −∇φ

and −∇φ

. The angles ϕ and ψ represent the geographical and the geocentric

latitudes.

Equation (1.60) is the general form of the equation of motion in the rotating

geographical coordinate system. If the deformation velocity is zero we obtain



=−2ρΩ × v − ρ ∇φ −∇p + µ ∇

v + (µ − λ) ∇(∇·v)

(1.62)

since ∇



= 0. Equation (1.62) applies to the rigidly rotating geographical

coordinate system. This is the form of the equation of motion given in most

textbooks. It should be clearly understood that the left-hand side of (1.60) represents

an artiﬁcial acceleration. The vertical line, as discussed, implies that the basis

vectors in v are not to be differentiated with respect to time.

The term −2ρΩ × v is the Coriolis force, which is a ﬁctitious force resulting

from the rotation of the coordinate system. An air parcel moving with the relative

velocity v will be deﬂected to the right in the northern hemisphere and to the left in

the southern hemisphere. Of course, the Coriolis force does not perform any work.

1.5 The energy budget of the general relative system

At the end of Section 1.2 we considered the energy budget with reference to the

absolute system. Now we wish to derive the energy budget for the general relative

system which includes not only the effects of rotation but also that of deformation.

As stated before, the total energy is given as the sum of the potential energy due to

gravitational attraction, the kinetic energy, and the internal energy. In the relative

system the relevant variables will be the geopotential instead of the gravitational

potential and the relative velocity instead of the absolute velocity. The budget

equation for the internal energy e will be included again, with a minor change in

148 The laws of atmospheric motion

the mathematical form that does not change its physical content. With v

= v +v

and v

= v



+ v

we may write for the total energy



= φ

+ e = φ +

+ e +



−

− φ



= φ +

+ e + χ (1.63)

where we have introduced the centrifugal potential according to (1.61). The

expression in parentheses is abbreviated by χ and may be rewritten as

χ =

(v + v

)

−



= v · v



(1.64)

where we have replaced φ

by means of (1.43). To describe the energy budget

we must obtain budget equations for each term in (1.63). We begin by adding the

budget equation of the gravitational attraction

dφ

= ρv

·∇φ

= ρ(v + v

) ·∇φ

since v



·∇φ

= 0(1.65a)

to the budget equation of the centrifugal potential

dφ

= ρv

·∇φ

= ρ(v + v

) ·∇φ

since v



·∇φ

= 0(1.65b)

which must have the same mathematical structure as (1.65a). This gives the budget

equation for the geopotential:

dφ

= ρ(v + v

) ·∇φ (1.66)

The next step is the derivation of the budget equation for the kinetic energy of

the relative system. On substituting (1.59a) into (1.58) we ﬁrst obtain

=−ρ ∇φ − ρΩ × (v + v

) − ρ

−∇·(p

E − J)(1.67)

where we have used the deﬁnition of the viscous stress tensor

J according to (1.12)

to simplify the notation. Scalar multiplication of (1.67) by v gives the required

budget equation for the kinetic energy:





+∇·[v·(pE −J)] =−ρv·∇φ−ρv·



Ω × v



+(pE −J)··∇v

(1.68)

The budget equation for χ is simply found by subtracting equations (1.65b) and

1.5 The energy budget of the general relative system 149

(1.68) from the second equation of (1.19). The complete energy budget for the

general relative system is listed as

(a)

(ρφ) = ρ(v + v

) ·∇φ

(b)





+∇·



v · (p

E − J)



=−ρv ·∇φ + (pE − J)··∇v

− ρv ·



Ω × v



(c)

(ρe) +∇·(J

+ F

) =−(pE − J)··∇(v + v

)

(d)

(ρχ) +∇·[(v



+ v

) · (pE − J)] =−ρv

·∇φ + (pE − J)··∇ v

+ ρv ·



Ω × v



(1.69)

In obtaining (1.69c) and (1.69d) we have used the rule that the double scalar product

of the symmetric dyadic (p

E − J) and the antisymmetric dyadic ∇v



vanishes.

Inspection of (1.69) shows that the sum of source terms on the right-hand

sides vanishes as required. Had we considered the budget of the geopotential

together with the budget equations of the kinetic energy and the internal energy

by themselves, then the sum of the source terms would not have vanished. To

correct this deﬁciency the budget equation of the quantity χ had to be introduced.

If desired, an energy ﬂux diagram for the budget (1.69) in the form of Figure 1.1

could be constructed.

Finally, it is also noteworthy that, in the absence of deformational effects (v

0), the budget (1.69) assumes a simpliﬁed form describing energetic processes in

the relative frame of the rigidly rotating coordinate system. Moreover, the right-

hand side of (1.69d) vanishes completely so that the budget of χ is free from

sources. Therefore, (1.69d) is no longer a part of the budget system, and we obtain

the simpliﬁed version of (1.69):

(a)

(ρφ) = ρv ·∇φ

(b)





+∇·



v · (p

E − J)



=−ρv ·∇φ + (pE − J)··∇v

(c)

(ρe) +∇·(J

+ F

) =−(pE − J)··∇ v

(1.70)

By comparing (1.70) with the energy budget of the absolute system (1.19), the

150 The laws of atmospheric motion

similarity of the expressions becomes apparent. In (1.70) the attractive potential φ

has been replaced by the geopotential φ and the absolute velocity v

by the relative

velocity v. In passing we would like to remark that the complete system (1.69) is

needed in order to describe the energetic processes of the general circulation.

1.6 The decomposition of the equation of motion

Let us consider the equation of motion (1.62), which is repeated for convenience

using the expansion (1.55). For reasons of brevity the ﬁnal two terms in (1.62) have

been rewritten as the divergence of the stress dyadic:

∂v

∂t



+v ·∇v +

∇p +∇φ + 2Ω × v −

∇·

J = 0

12345 6

(1.71)

The physical meaning of each term will now brieﬂy be explained. Term 1 describes

the local change of the velocity whereas the nonlinear term 2 represents the advec-

tion of the velocity. Term 3 is most easily comprehended and is usually called the

pressure gradient force. Term 4 combines the absolute gravitational force and the

centrifugal force into a single force often called the apparent or relative gravity.It

is this gravity which is actually observed on the earth. Any surface on which φ is

constant is called a level surface or equipotential surface. There is no component

of the apparent gravity along such surfaces. Motion along level surfaces is usually

referred to as horizontal motion. Multiplying term 5 in (1.71) by −1resultsin

the Coriolis force, which has already been discussed, whereas term 6 represents

frictional effects.

For prognostic purposes it is necessary to decompose the vector equation (1.71)

into three equations for the components of the wind ﬁeld in each direction. There

are various ways to obtain the component equations. In order to resolve (1.71)

we assume that surfaces of constant geopotential are spherical. The ﬁrst step is to

obtain the metric fundamental quantities g

. It is best to employ the basic deﬁnition

(a) dr · dr = dq

· dq

= g

(b) dr = r cos ϕdλe

+ rdϕe

+ dr e

, q

= e

√

, e

= e

(1.72)

The increment dr stated in (1.72b) can be easily found from inspection of

Figure 1.2. The orthogonal system of the spherical earth is completely described

by only three fundamental quantities:

= r

cos

ϕ, g

= r

= 1,g

= 0fori = j (1.73)

in agreement with (1.31).