Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


2.3 Scale analysis of large-scale frictionless motion 161
The dimensionless flow numbers (2.8) assume the practical forms
St =
VT
l
S
=
V
C
,Ro=
V
2S
,Eu=
V
2
R
0
T
0
Fr =
V
2
GS
,Re=
VS
Aµ
0
=
VS
ν
0
(2.16)
The equation of motion (1.71) in scale-analytic form can now be written as
V
T
l
∂v
∂t
q
i
+
V
2
S
v ·∇v
+
AP
S
1
ρ
∇p
− G
∇φ
+ 2V
Ω × v
−
Aµ
0
V
S
2
1
ρ
∇·
J
= 0
(2.17)
Dividing this equation by the magnitude of the inertial force and using the practical
forms of the flow numbers (2.16) again yields (2.9).
The scale-analytic form of the Navier–Stokes equation may be used to estimate
the relative importance of each term. For many applications, however, it is of
advantage not to subject the vector equation (2.9) directly to a scale analysis but
to use the equivalent scalar equations. How to proceed for large-scale frictionless
flow will be explained in the next section. The effect of friction will be treated in
a later chapter when we have acquired the necessary background. In passing, we
would like to remark that the method of scale analysis is quite general and may be
applied not only to the equation of motion but also to other equations.
2.3 Scale analysis of large-scale frictionless motion
As stated before, we wish to apply the method of scale analysis to the scalar form
of the equation of motion. We describe the motion in spherical coordinates in the
form (1.84). In order to proceed efficiently, we apply equation (2.3) to the latitude
and longitude, height, time, and other pertinent variables, yielding
(a) λ
*
= L
λ
*
,ϕ
*
= L
ϕ
*
,z= D
z
(b) u = U
u
,v= U
v
,w= W
w
(c) t = T
l
t
=
L
C
t
(d) g = G
g
,p= P
p
(e) H
p
= H
0
H
p
,R
0
T = gH
p
= GH
0
gH
p
(f) f = f
0
f
,l= l
0
l
(g) r = a
(2.18)
162 Scale analysis
The stars labeling latitude and longitude, as defined by (1.75), are to remind us that
we are using physical measure numbers. From observations it is known that the
large scales of motion in longitudinal and latitudinal directions are of the same order
of magnitude L whereas the vertical scale D is quite different, see (2.18a). The
same is true for the magnitudes of the horizontal (U )andvertical(W ) components
of the wind velocity. Equations (2.18c) and (2.18d) give the scaled forms of time,
of the acceleration due to gravity, and of the pressure p. It is also customary to
introduce the pressure scale height H
p
as given by (2.18e). The Coriolis parameters
f and l are scaled in (2.18f) whereby the suffix 0 refers to the mean latitude of a
geographical latitude belt for which the motion is considered. Finally, the radius r
may be replaced by the mean radius a of the earth.
According to observations in the atmosphere the following typical numerical
values are used for the quantities occurring in (2.18)
1
U ∼ 10 m s
−1
,W≤ 0.1ms
−1
,C≤ U
L ∼ 10
6
m,D= H
0
∼ 10
4
m
G ∼ 10 m s
−2
,a∼ 10
7
m
l
0
∼ 10
−4
s
−1
,f
0
∼
10
−4
s
−1
for 25
◦
≤ ϕ
0
≤ 80
◦
10
−5
s
−1
for ϕ
0
< 25
◦
(2.19)
It is seen that the characteristic vertical velocity is much smaller than the
characteristic horizontal velocity so that W U. Furthermore, the phase velocity
C of synoptic systems such as ridges and troughs satisfies the inequality C ≤ U
so that, according to (2.16), the Strouhal number is St ≥ 1. Therefore, the local
time scale T
l
= S/C is larger than or equal to the so-called convective time scale
T
c
= S/U,i.e.T
l
≥ T
c
. The latitudinal dependence of the Coriolis parameter f
0
is accounted for by using different values for the two geographical latitude bands
25
◦
≤ ϕ
0
≤ 80
◦
representing the broad range of mid- and high latitudes and
ϕ
0
< 25
◦
for the low latitudes.
Using (2.18) the pressure-gradient force terms appearing in (1.84) may be written
as
1
ρ
∂p
∂λ
*
=
gH
p
p
∂p
∂λ
*
=
GH
0
L
,p
h
P
gH
p
p
∂p
∂λ
*
1
ρ
∂p
∂ϕ
*
=
gH
p
p
∂p
∂ϕ
*
=
GH
0
L
,p
h
P
gH
p
p
∂p
∂ϕ
*
1
ρ
∂p
∂z
=
gH
p
p
∂p
∂z
=
GH
0
D
,p
v
P
gH
p
p
∂p
∂z
(2.20)
1
If dynamic processes of the boundary layer, where friction cannot be ignored, are being investigated, then we
must use D = 10
3
m.
2.3 Scale analysis of large-scale frictionless motion 163
In these expressions the magnitudes of the spatial pressure changes ,p
h,v
have
been introduced, whereby the subscripts h and v have been added in order to
distinguish between horizontal and vertical pressure changes. However, as the
expressions suggest, it is profitable to approximate the magnitudes of the rela-
tive pressure changes ,p
h,v
/P . From observations we find the following typical
values:
,p
h
P
∼
10
−2
for 25
◦
≤ ϕ
0
≤ 80
◦
10
−3
for ϕ
0
< 25
◦
,
,p
v
P
∼ 1(2.21)
The vertical pressure change refers to the entire vertical extent H
0
of the atmosphere.
Observations indicate that the magnitudes of the changes in velocity along the
horizontal and vertical length scales are similar and equal to the order of magnitude
of the velocity:
,u
h
∼ U, ,u
v
∼ U, ,v
h
∼ U, ,v
v
∼ U (2.22)
Now we have finished all preparatory work for the scale analysis of the equation
of motion in the scalar form. By substituting (2.20) for the pressure-gradient terms
into (1.84) and using the scale-analytic expressions given in the previous equations,
we obtain without difficulty
CU
L
∂u
∂t
+
U
2
L
u
∂u
∂λ
*
+
v
∂u
∂ϕ
*
+
UW
H
0
w
∂u
∂z
+
UW
a
uw
(i) ∼10
−4
∼10
−4
∼10
−4
∼10
−7
(ii) ∼10
−4
∼10
−4
∼10
−4
∼10
−7
12 34
−
U
2
a
tan ϕ
uv
+ l
0
W
lw
−f
0
U
fv
+
GH
0
L
,p
h
P
gH
p
p
∂p
∂λ
*
= 0
(i) ∼10
−5
∼10
−5
∼10
−3
∼10
−3
(ii) ∼10
−5
∼10
−5
∼10
−4
∼10
−4
567 8
(2.23a)
164 Scale analysis
CU
L
∂v
∂t
+
U
2
L
u
∂v
∂λ
*
+
v
∂v
∂ϕ
*
+
UW
H
0
w
∂v
∂z
+
UW
a
vw
(i) ∼10
−4
∼10
−4
∼10
−4
∼10
−7
(ii) ∼10
−4
∼10
−4
∼10
−4
∼10
−7
12 34
+
U
2
a
u
2
tan ϕ +f
0
U
fu
+
GH
0
L
,p
h
P
gH
p
p
∂p
∂ϕ
*
= 0
(i) ∼10
−5
∼10
−3
∼10
−3
(ii) ∼10
−5
∼10
−4
∼10
−4
57 8
(2.23b)
CW
L
∂w
∂t
+
UW
L
u
∂w
∂λ
*
+
v
∂w
∂ϕ
*
+
W
2
H
0
w
∂w
∂z
(i) ∼10
−6
∼10
−6
∼10
−6
(ii) ∼10
−6
∼10
−6
∼10
−6
12 3
−
U
2
a
u
2
+
v
2
− l
0
U
lu
+ G
,p
v
P
gH
p
p
∂p
∂z
+ G
g
= 0
(i) ∼10
−5
∼10
−3
∼10
1
∼10
1
(ii) ∼10
−5
∼10
−3
∼10
1
∼10
1
4689
(2.23c)
Below each term we have written the approximate magnitudes for the two latitude
bands (i) 25
◦
≤ ϕ
0
≤ 80
◦
and (ii) ϕ
0
< 25
◦
. For ease of identification the
terms have also been numbered. Each term is the product of a dimensional factor
representing force per unit mass and of dimensionless quantities
···
of
magnitude 1. Comparison of individual terms then shows which terms may be
safely omitted in large-scale frictionless motion.
Let us first consider the prognostic equation (2.23a) for the u-component of the
wind field. Term 1 representing the local rate of change with time of the velocity
and terms 2 and 3 denoting horizontal and vertical advection are all of the same
order of magnitude 10
−4
. Terms 4 and 5 both involve the radius a of the earth.
Since term 4 is at least two orders of magnitude smaller than the remaining terms,
it may be safely ignored. Terms 6 and 7 are due to the earth’s rotation and represent
2.3 Scale analysis of large-scale frictionless motion 165
the Coriolis force. The main effect of the Coriolis force is included in term 7, so
term 6 may be omitted. One might be tempted to also ignore term 5, which is
of the same magnitude as term 6, but these two terms represent entirely different
forces. Term 5 is a metric acceleration and should be retained in comparison with
the metric acceleration term 4. Metric accelerations are apparent accelerations
resulting from the particular shape of the coordinate system being considered.
They do not perform any work. The estimated magnitude of the pressure-gradient
term shows that this term must be retained under all circumstances. The same type
of argument may be applied to equation (2.23b) describing the equation for the
v-component of the wind field. Only the metric term 4 will be ignored due to its
small magnitude.
A somewhat different situation arises in (2.23c). Inspection shows that the
vertical pressure gradient and the gravitational effect represented by terms 8 and 9
are of the same order of magnitude and seven orders of magnitude larger than the
individual acceleration represented by the terms 1–3. Moreover, terms 4 and 6 may
also be ignored in comparison with terms 8 and 9, so this equation degener
ates to
two terms only. Nevertheless, we will momentarily retain terms 1–3 adding up to
the individual vertical acceleration. The analysis of some small-scale circulations
can be carried out only if the vertical acceleration is accounted for.
The information gained by the above scale analysis may now be utilized to
obtain the approximate form of the equation of motion (1.84) for the components
u, v, w of the wind field in the geographical coordinate system for the description
of large-scale frictionless flow fields
∂u
∂t
+
u
a cos ϕ
∂u
∂λ
+
v
a
∂u
∂ϕ
+ w
∂u
∂z
−
uv
a
tan ϕ − fv =−
1
ρa cos ϕ
∂p
∂λ
∂v
∂t
+
u
a cos ϕ
∂v
∂λ
+
v
a
∂v
∂ϕ
+ w
∂v
∂z
+
u
2
a
tan ϕ + fu =−
1
ρa
∂p
∂ϕ
∂w
∂t
+
u
a cos ϕ
∂w
∂λ
+
v
a
∂w
∂ϕ
+ w
∂w
∂z
=−
1
ρ
∂p
∂z
− g
(2.24)
Recalling the definition of the individual derivative
d
dt
=
∂
∂t
+
u
a cos ϕ
∂
∂λ
+
v
a
∂
∂ϕ
+ w
∂
∂z
with u = a cos ϕ
˙
λ, v = a ˙ϕ, w = ˙r
(2.25)
the three components of the equation of motion in their approximate form may be
rewritten as
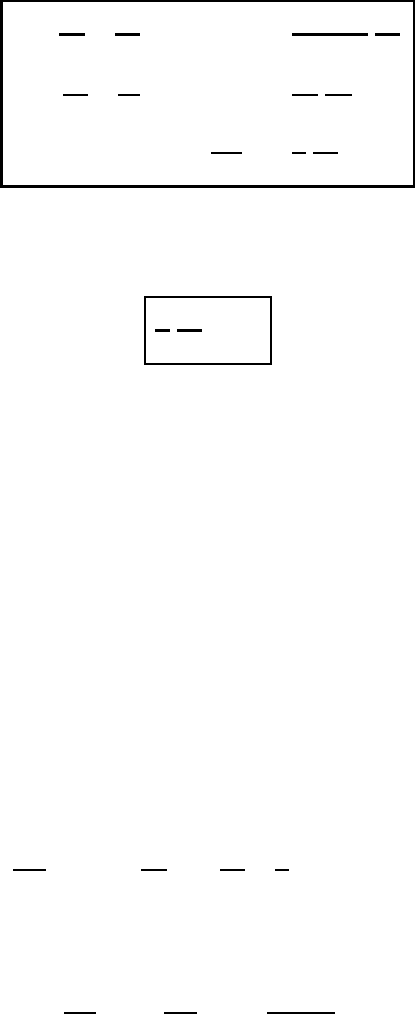
166 Scale analysis
(a)
du
dt
−
uv
a
tan ϕ − fv =−
1
ρa cos ϕ
∂p
∂λ
(b)
dv
dt
+
u
2
a
tan ϕ + fu=−
1
ρa
∂p
∂ϕ
(c)
dw
dt
=−
1
ρ
∂p
∂z
− g
(2.26)
Owing to the small magnitudes of terms 1 to 3 in (2.23c) for large-scale motion,
which combine to give the vertical acceleration, we need to retain only terms 8 and
9. For this reason (2.26c) degenerates to
1
ρ
∂p
∂z
=−g
(2.27)
This equation is known as the hydrostatic approximation. The large-scale or the
synoptic-scale motion is quasistatic even in the presence of horizontal gradients of
the thermodynamic variables (p, T , ρ). We must clearly understand that quasistatic
motion does not imply that there is no vertical motion since w is still contained in
the advection term of (2.24). In fact, we have not set dw/dt = 0 but used scale
analysis to show that the absolute value of dw/dt is much smaller than the absolute
values of the vertical pressure gradient and the acceleration due to gravity. If the
third equation of motion (2.26c) is replaced by (2.27) it is no longer available for
the prognostic determination of w, which must be obtained in some other way. The
large-scale motion is then characterized by equations (2.26a) and (2.26b) together
with equation (2.27).
We will now multiply (2.26a) and (2.26b) by the unit vectors e
λ
and e
ϕ
,
respectively, and then add these two equations representing the horizontal
motion. The two terms containing tan ϕ may be combined to give a vector
expression representing the metric acceleration. For brevity, we also combine the
two acceleration terms (du/dt,dv/dt) with the metric acceleration, yielding
dv
h
dt
e
i
h
= e
λ
du
dt
+ e
ϕ
dv
dt
+
u
a
tan ϕ (e
r
× v
h
)(2.28a)
with v
h
= e
λ
u + e
ϕ
v. This is the horizontal part of the total acceleration of the
horizontal wind given by
dv
h
dt
e
i
=
dv
h
dt
e
i
h
−
u
2
+ v
2
a
e
r
(2.28b)
The last term of this equation appears in (2.23c). Recall that the vertical line in
the differential operator on the left-hand side symbolizes that the unit vectors are
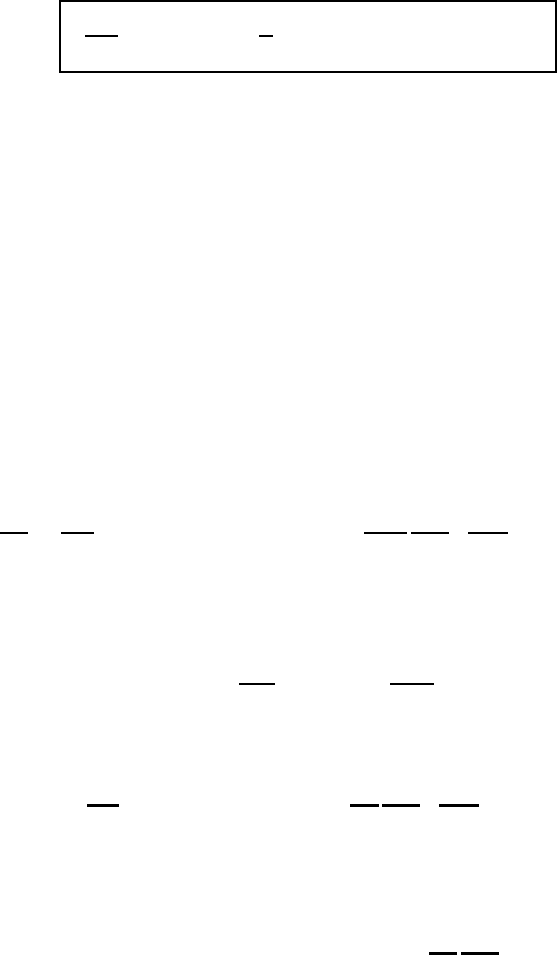
2.4 The geostrophic wind and the Euler wind 167
not to be differentiated with respect to time. Likewise, the two terms containing
the Coriolis parameter may be combined to give C
h
, which is an approximate
expression for the Coriolis force. Therefore, the equation of horizontal motion may
be written in simplified form as
dv
h
dt
e
i
h
− C
h
=−
1
ρ
∇
h
p with C
h
=−f e
r
× v
h
(2.29)
From (2.29) it can be seen that the Coriolis force C
h
is oriented normal to v
h
.Inthe
northern (southern) hemisphere the Coriolis force is pointing to the right (left) if
the observer is looking in the direction of the horizontal wind. This approximation
is also valid at low latitudes with the exception of the equatorial belt. Even at the
latitude of ϕ =±5
◦
the term lw appearing in (2.23a) is one order of magnitude
smaller than fv.
2.4 The geostrophic wind and the Euler wind
We wish to consider the magnitudes of the various terms of (2.29). Inspection of
(2.23a) and (2.23b) shows that, at mid- and high latitudes, the individual derivatives
du/dt,dv/dt and the metric acceleration are at least one order of magnitude
smaller than the components of C
h
and the horizontal pressure gradient. This is
also apparent from the scaling of (2.29):
U
2
L
dv
h
dt
e
i
h
+ f
0
U
f e
r
× v
h
=−
GH
0
L
,p
h
P
gH
p
p
∇
h
p
(2.30)
where the upper limit C = U has been used. By utilizing in (2.16) the magnitudes
listed in (2.19) we obtain for the Rossby and Froude numbers
Ro =
U
f
0
L
,Fr=
U
2
GH
0
(2.31)
Substitution of these expressions into (2.30) yields
Ro
dv
h
dt
e
i
h
+
f e
r
× v
h
=−
Ro
Fr
,p
h
P
gH
p
p
∇
h
p
(2.32)
For the large-scale synoptic flow regimes at the mid- and high latitudes we obtain
from (2.19) and (2.21)
25
◦
≤ ϕ
0
≤ 80
◦
: Ro ∼ 10
−1
,
Ro
Fr
,p
h
P
∼ 1(2.33)

168 Scale analysis
p − ∆ p
Fig. 2.1 The geostrophic wind in the northern hemisphere.
In the limiting case (L very large so that Ro → 0, but (u, v) = 0), we find from
(2.32) an exact balance between the Coriolis force and the pressure-gradient force.
The wind resulting from this balance is known as the geostrophic wind v
g
and may
be easily obtained from (2.29), which reduces to
f e
r
× v
g
=−
1
ρ
∇
h
p (2.34)
On solving for v
g
we find
v
g
=
1
ρf
e
r
×∇
h
p
(2.35)
The isobars run parallel to the geostrophic wind vector so that v
g
is normal to
the pressure-gradient force. According to (2.34) the directions of the Coriolis
force and the pressure-gradient force are opposite, as shown in Figure 2.1 for
the northern hemisphere. Above the atmospheric boundary layer where frictional
effects are very small, the geostrophic wind deviates very little from the actu-
ally observed wind. However, this small deviation is very important since it is
responsible for atmospheric developments. Owing to its smallness, the geostrophic
deviation in the free atmosphere can hardly be determined from routine measure-
ments.
Let us briefly consider the tropical latitudes. In this situation we obtain from
(2.19) and (2.21) (see also Charney (1963))
ϕ
0
< 25
◦
: Ro ∼ 1,
Ro
Fr
,p
h
P
∼ 1(2.36)
Approaching the equator either from the south or from the north, the Rossby number
becomes very large so that the Coriolis term in (2.32) may be ignored. This reduces

2.6 Problems 169
(2.29) to the horizontal form of the Euler equation:
dv
h
dt
e
i
h
=−
1
ρ
∇
h
p
(2.37)
which is the equilibrium condition at ϕ = 0
◦
and very near to the equator.
2.5 The equation of motion on a tangential plane
Let us briefly review the scale-analyzed equation of motion (2.26) of the rotating
spherical-coordinate system. The singularites at the poles (ϕ =±90
◦
)arising
from cos ϕ and tan φ are troublesome. Later, when we introduce the so-called
stereographic coordinate system, these singularities disappear. At this point it will
be very convenient for us to introduce a rotating rectangular coordinate system
in which the x-axis is pointing toward the east, the y-axis toward the north, and
the z-axis toward the local zenith. This type of coordinate system is sufficient for
the study of various meteorological problems. We will reduce equation (2.26) by
“brute strength” to obtain the desired result.
We imagine a plane that is tangential to the spherical earth at a selected point.
The rotational speed of the plane is sin ϕ = f/2, as follows from inspection of
Figure 1.4. By omitting from (2.26) the two terms containing tan ϕ and by replacing
the increments of the physical coordinates (see equation (1.75))
δλ
∗
= a cos ϕ δλ
and
δϕ
∗
= a δϕ in the pressure-gradient force by δx and δy, respectively, we obtain
the equation of motion for the tangential plane:
du
dt
− fv =−
1
ρ
∂p
∂x
dv
dt
+ fu=−
1
ρ
∂p
∂y
dw
dt
=−
1
ρ
∂p
∂z
− g
(2.38)
We shall use this form of the equation of motion from time to time.
2.6 Problems
2.1: Check whether the magnitudes in (2.23) are correct. Use the numerical values
stated in the text.
170 Scale analysis
2.2: Verify equation (2.28b).
2.3: Let M
λ
, M
ϕ
,andM
r
represent the metric accelerations.
(a) With the help of (2.23) write down proper expressions for M
λ
, M
ϕ
,andM
r
.
(b) Show that the metric acceleration does not perform any work.
2.4: The equation of motion can be written as
∂ρv
∂t
q
i
=−∇·(ρvv) −∇·(pE − J) − ρ ∇φ + 2ρv ×
with
J = µ(∇v + v
∇−
2
3
∇·vE)
2Ω = 2 cos ϕ i
2
+ 2 sin ϕ i
3
= f
2
i
2
+ f
3
i
3
Show that the component form of this equation in Cartesian coordinates is given
by
∂ρ u
i
∂t
=−
∂
∂x
n
(ρu
n
u
i
) + 2
imn
f
n
ρu
m
−
∂p
∂x
i
− δ
i3
ρg
+
∂
∂x
n
µ
∂u
i
∂x
n
+
∂u
n
∂x
i
−
2
3
δ
in
∂u
m
∂x
m
with i
1
·A × B = 2
imn
A
m
B
n
2
ij k
=
1for(i, j, k) = (1, 2, 3), (2, 3, 1), (3, 1, 2)
−1for(i, j, k) = (3, 2, 1), (2, 1, 3), (1, 3, 2)
0else
