Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.


Методи врівноваження багатьох виміряних величин
х. +
v.
(/ =
1,
п) як для величин X. (/ =
1,
гі), так
і
для врівноважених значень / (у
параметрів Т (j = l,k)
Х
І
+ V
,
=
Л*v
1
2>
О (' = Ь")'
звідки отримаємо систему рівнянь (5.7), які називаються параметри
1
рівняннями поправок
v, =/(*,, t
2
,..., t
k
)-x., і = \,п.
Для цього випадку умову (5.5) запишемо у вигляді
F = ip
i
[f
i
{ti,h,...,t
k
)-x
i
]
2
=[p-{f-x)
1
] = [p-v
2
]^ min.
і=і
Функція Fe функцією параметрів t (j = i,k), тобто задача на ум
екстремум звелася до задачі на абсолютний екстремум функції F
і
для тог
знайти мінімум функції F, потрібно мати її часткові похідні 1-го поря/
аргументами t (j = ІД). Продиференціюємо вираз (5.8) за змінними t. (j =
отримані співвідношення прирівняємо до нуля (необхідна умова екстр
функції). У результаті отримаємо систему к рівнянь із к невідомими t. (j =
8v
dF n dVj
Ц l^'dTj
pv
Tt
= 0, j = \,k.
Система рівнянь (5.9) називається системою нормальних рівнянь у загаї
вигляді. Розв'язавши її, одержимо врівноважені значення параметрів t (j
після чого із використанням параметричних рівнянь поправок (5.7) знг
поправки v. (і -1, гі) до результатів вимірювань х
1
(і -1 ,гі).
Однак у загальному випадку система рівнянь (5.9) є нелінійною і отри
розв'язок складно. Тому наведену систему нелінійних рівнянь слід лінеари:
Для цього якимось чином потрібно знайти наближені значення t°(j
параметрів t (j =
l.jfc)
і врівноважені значення подати так:
tj=t'j+TjU = Vc), (
де т. (j = ІД) - поправки до наближених значень t°(j -1 ,к) параметрів t
}
(j
Наближені значення t°(j-\,k) визначають якомога точніше, щоб поі
т. (j = 1 ,к) були достатньо малими.
Із використанням рівностей (5.10), систему рівнянь (5.7) перепишемо у і

294
Розділ V
У
і
=/
і
(Г
1
+г
1
,Ґ
2
+г
г
,...,Г
к
+т
к
)-х
і
, i = l,n. (5.11)
Припустимо, що функції(г' = 1,л) є такими, що їх можна розкласти в ряд
Тейлора в околі точки ,tl,...,t°
k
). Оскільки поправки т. (j = l,k) є малими, то
обмежившись лінійними членами розкладу одержимо
7=1
dt,
•т, -х,. (г' = 1,и),
або, ввівши позначення
=
a
i,
f
3/,
l
= b
t
, ...,
dt,
V
1
I
»
0
dt,
\
1
J
19
• • * >
0
w
= и.
(5.12)
отримаємо систему (5.13) параметричних рівнянь у лінійному вигляді
v. = а.т, +
Ь.т
2
+ ... +
и.т
к
+ /., / = 1 ,п . (5.13)
У цих рівняннях невідомими є поправки
v.
до виміряних значень х. (і =
1,
п) та
поправки т. до наближених значень параметрів t
°
(у =
1,
к). Тому наведена система
параметричних рівнянь (5.13) є недовизначеною, оскільки кількість невідомих
дорівнює п + к, а кількість рівнянь - п.
Для розв'язання системи рівнянь (5.13) застосуємо метод найменших квадратів,
поданий співвідношенням (5.8). Умова \pv
2
]—шіп із врахуванням співвідношень
(5.13) запишеться так:
[pv
2
] = tp
l
(a,T
l
+Ь
і
т
2
+ ... + u
i
r
k
+/,.)
2
=F(T
l
,T
2
,...T
k
)-*min.
/=і
Для знаходження мінімуму функції ^знайдемо її часткові похідні за змінними
т (j = 1,к) та прирівняємо їх до нуля. Із врахуванням виразів (5.13) у результаті
отримаємо систему к лінійних рівнянь із к невідомими т. (j = 1 ,к)
dF «
— = 2^р,а,
(а,т,
+
Ь,т
2
+... + и,т
к
+
/,•)
= 2 [pav] = 0
8т
dF
/=і
T^Pfb, (а,,т, +
Ь,т
2
+... + и
і
г
к
+/,.) = 2 [pbv] = 0
ОТ, /=1
(5.14)
dF
dt.
= 2Y
i
p
i
u
j
(a
j
T
x
+Ь
і
т
2
+ ... + и
і
т
к
+
lj)
= 2[puv] = 0.
i=i

Методи врівноваження багатьох виміряних величин
Скоротивши на 2 кожне з рівнянь системи (5.14) та розкривши
приходимо до нормальної системи лінійних алгебраїчних рівнянь для знахс
поправок т. (j = ІД)
[ра
2
]т, + [pab]
т
2
+... + [раи]т
к
+ [раї] = 0
[pab] т, + [pb
2
]т
2
+...+ [pbu] т
к
+ [pbl] = 0
[рай] т, +[pbu] т
2
+ ... + [ри
2
]т
к
+[pul] = 0.
Система рівнянь (5.15) є нормальною тому, що на головній її ді
знаходяться так звані квадратичні коефіцієнти [pa
2
], [pb
2
], ..., [ри
2
], які є
додатніми, а симетричні відносно головної діагоналі коефіцієнти є рівн*
Для рівноточних вимірювань нормальна система лінійних алгеб
рівнянь запишеться так:
[а
2
] т, + [ab] т
2
+... + [аи] т
к
+ [аі] = 0
[аЬ]т
х
+[Ь
2
] т
2
+... + [bu]x
k
+ [bl] = 0
[аи] т, +
[Ьи]т
2
+ ... + [и
2
]т
к
+[ul] = 0.
Розв'язавши систему рівнянь (5.15) або (5.16) довільним методом і
невідомих т. (j = 1,к) та підставивши їх знайдені значення у вирази (5.13), з
поправки v. та врівноважені значення х. + v. виміряних величин х
(
. (і =
1, п
перша частина задачі врівноваження параметричним методом є розв'
Другою частиною задачі врівноваження є знаходження оцінки точності
BV
величин. Щоб перейти до розгляду знаходження оцінки точності, розгляне
методи розв'язування нормальних систем лінійних алгебраїчних рівнянь,
цього спочатку подамо параметричний метод врівноваження у матричному
§ 5.3. Матричне подання параметричного методу врівноваж
Розглянемо систему параметричних рівнянь поправок у лінійному
(5.13). Введемо матрицю А коефіцієнтів даної системи розмірності пхк
/ і \
А,О, ...М,
296
Розділ V
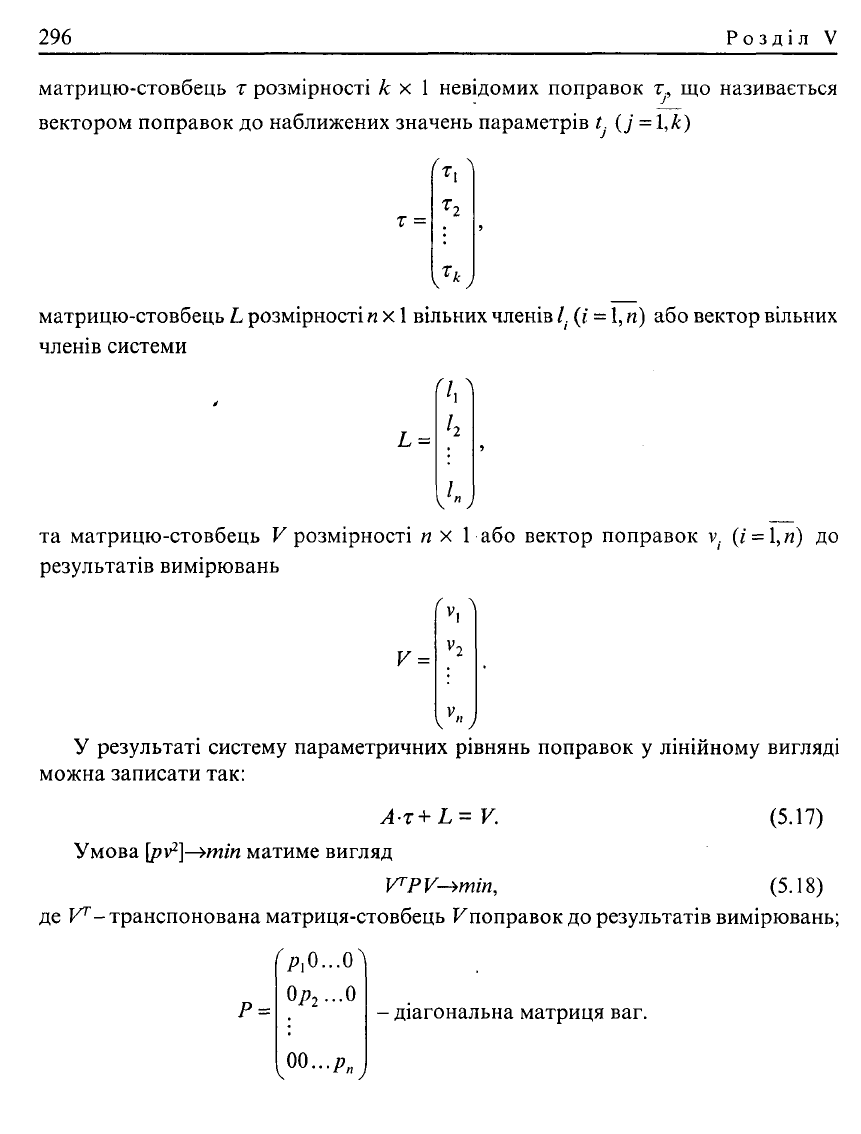
матрицю-стовбець т розмірності к х 1 невідомих поправок т., що називається
вектором поправок до наближених значень параметрів t (j = \,к)
т
=
с ~ \
V
А
/
матрицю-стовбець L розмірності
п
х
1
вільних членів /. (і =
1,
п) або вектор вільних
членів системи
Ґ1 \
L =
К
1
-
та матрицю-стовбець V розмірності п х 1 або вектор поправок v. (і = \,п) до
результатів вимірювань
V =
Ґ \
ч
V
\ " J
У результаті систему параметричних рівнянь поправок у лінійному вигляді
можна записати так:
А-т+ L= V. (5.17)
Умова [pv
2
]—>min матиме вигляд
VPV-bmin, (5.18)
де V-транспонована матриця-стовбець Кпоправок до результатів вимірювань;
Рі
0...0'
0р
2
...0
00 ...р„
- діагональна матриця ваг.

Методи врівноваження багатьох виміряних величин
Справді,
V
T
PV = (v
{
,v
2
,...,v
n
)
Рх
О...О
Ор
2
...о
v
V
'v
= (v
lP]
,v
2
p
2
,...,v
n
p
n
)-
•p
x
v
2
+p
2
v
2
2
+... + p
n
v
2
n
=[pv
2
}.
Функція F 'n використанням співвідношень (5.17) та (5.18) набуде вигля
F= (AT + L)
2
•
P
•
(Аг + L), (5
а необхідна умова мінімуму для функції
F,
виражена системою (5.14) запишетьс
A
T
PV = 0.
(5
Покажемо це.
А
•
Р-V =
а
х
а
2
...а
п
Ь
х
Ь
2
...Ь
п
VIj U*)
і!, W^j
до...о'
0 р
2
...о
0 0 ...р
п
Л, Л
\
V
"J
а
хРх
а
2
р
2
...а
п
р„
Ь
]Рх
Ь
2
р
2
...Ь
п
р
п
и
1
р
]
и
2
р
2
...и
п
р
п
v
A "J
a
\P\
v
\ +
a
2P2
v
2+--- + a
n
P„v
n
b
x
p
x
v
x
+b
2
p
2
v
2
+... + b„i>
n
v„
\
'[pav\
S
=
[pbv]
)
[puv]
/
= 0.
u
xPx
v
x
+u
2
p
2
v
2
+... + u
n
p
n
v„
Нами отримано умови, які є аналогічні умовам, вираженим системою (
Необхідну умову мінімуму (5.20) для функції F перепишемо, викорисі
матричне рівняння (5.17), тобто
A
t
PV=A
t
P-(AT+L) = A
t
PAz + A
t
PL = 0. (Ї
Рівняння (5.21) називається матричним нормальним рівнянням попр
Покажемо, що воно є еквівалентним системі рівнянь (5.15). Для цього розп*
доданки, які входять у рівність (5.21).
А
Т
РАт=
а
х
а
2
...а
п
Ь
х
Ь
2
...Ь
п
и
х
и
2
...и
п
Рх
0...0
0 р
2
...0
0 0 ...р
п
а
х
Ь
х
...и
х
а
2
Ь
2
...и
2
а
п
Ь
п
...и
п

298
Розділ V
ґа
\Р\ а
2
р
2
...а
п
р„
Л
b
lPl
b
2
p
2
...b
n
p„
ЩРх
и
гРі •••
и
пРп
...и,
а
2
Ь
2
...и
2
a b ...и
V
Л
/
[а
2
р] [abp]... [аир] (
[,abp][b
2
p]...[bup]
[аир] [Ьир]... [и
2
р]
т
2
т
к
V
К
/
/ ? \
[а р]т, + [а6р]т
2
+... + [ямріт*
+ [Ь
2
р] т
2
+... +
[Ьир]т
к
[аир] т, + [6ир]т
2
+ ... + [м
2
/?]Гд
А
т
PL =
а
2і
р
2
...л
и
/>
я
У/,
ь
іРі •••
Ь
пРп
U
\P\ U
2
P2---U
n
P
n
A
1
"
J
[арі]
[bpl]
[ирі]
А
Г
РАх + А
т
PL-
[а
2
р]
т,
+
[а6р]т
2
+... + [аир]т
к
+[apl]
[abp]
т,
+ [Ь
2
р] т
2
+... +
[Ьир]т
к
+ [bpl]
[аир]т, +[Ьир]г
2
+ ... + [и р]г
к
+[upl]
Як видно з отриманої рівності, права її частина є еквівалентною лівим
частинам рівнянь системи (5.15), що і треба було довести.
А тепер перейдемо до розгляду основних методів розв'язування нормальних
систем лінійних алгебраїчних рівнянь.
§ 5.4. Деякі методи розв'язування нормальних систем
лінійних алгебраїчних рівнянь.
5.4.1. Метод Ґаусса
Даний метод є точним. Він використовується для розв'язування довільної
системи лінійних алгебраїчних рівнянь та полягає у послідовному усуненні
невідомих. Наближений розв'язок із використанням даного методу отримується
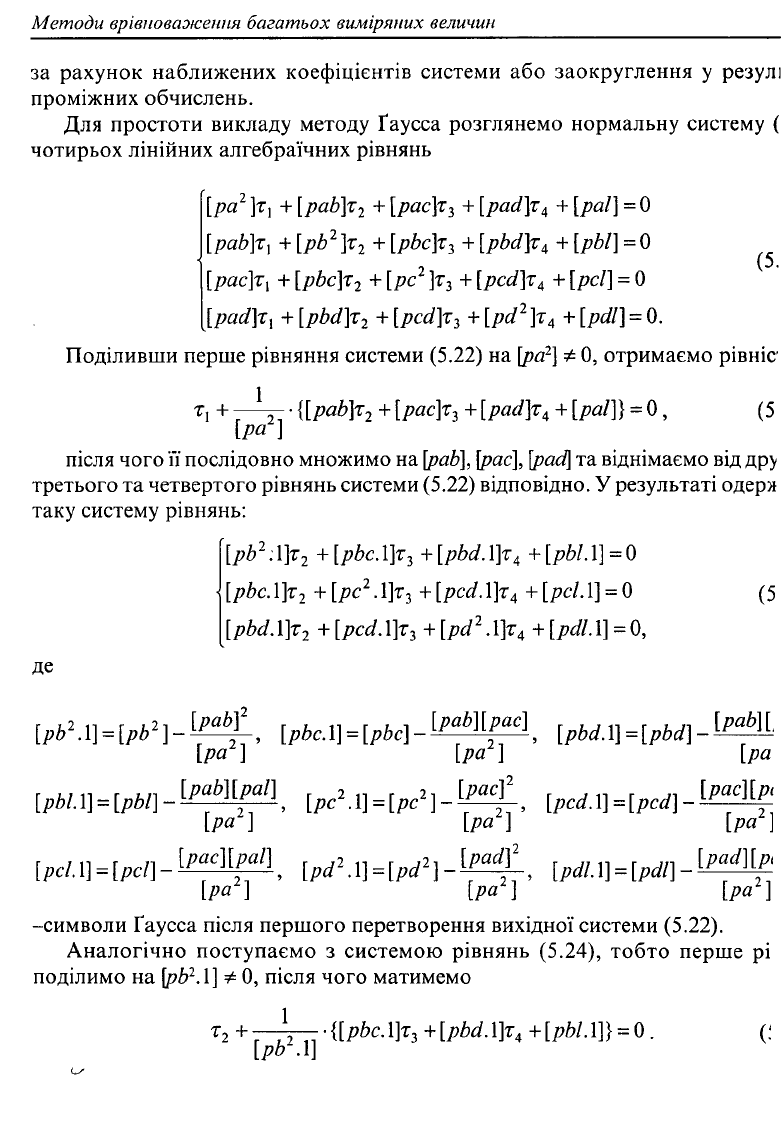
Методи врівноваження багатьох виміряних величин
за рахунок наближених коефіцієнтів системи або заокруглення у резулі
проміжних обчислень.
Для простоти викладу методу Ґаусса розглянемо нормальну систему (
чотирьох лінійних алгебраїчних рівнянь
[ра
2
]т, + [pab] г
г
+ [рас)т
г
+ [pad] т
4
+ [раї] = 0
[pab] т, + [pb
2
]т
2
+ [pbc]r з + [pbd]z
4
+ [pbl] = 0
[рас]т
[
+ [pbc] т
2
+ [рс
2
]т
3
+ [pcd] т
4
+ [реї] = 0
[pad] т, + [pbd]z
2
+ [pcd] т
3
+ [pd
2
]т
4
+ = 0.
Поділивши перше рівняння системи (5.22) на [ра
2
]
Ф
0, отримаємо рівніс
т, + -А—
•
{[/ю6]т
2
+ [рас]т
3
+ [/ки/]т
4
+ [ра/]} = 0, (5
[ра ]
після чого її послідовно множимо на
[pab],
[рас],
[pad]
та віднімаємо від дру
третього та четвертого рівнянь системи (5.22) відповідно. У результаті одеря
таку систему рівнянь:
[pb
2
:\]т
2
+ [pbc.l]T
3
+[pbdA]z
4
+[pblA] = 0
• [pbc. 1]т
2
+ [рс
2
.1]т
3
+ [pcd. 1]т
4
+ [pel.
1]
= 0 (5
[pbd. 1]т
2
+ [pcd.
1]т
3
+ [pd
2
.1]т
4
+ [pdl.
1]
= 0,
де
[рЬ
2
Л] = [рЬ
2
]-
[
>^%, [pbcA] = [pbc]-
[
-^M^, [pbdA] = [pbd]-lE^
[ра ] [ра ] [ра
[pblA] = [pbl]-MM, [рс
2
ЛМ
Р
с
2
]-
[
-^-, [pcdA] = [pcd]-\^M^
[pa] [pa
2
] [
P
a
2
]
[рсІЛМрсЦ-^Щ^, [
P
d
2
A
Mp
d
2
]-Ml,
[pd
lA
Mpdri
J-P^M
[pa ] [pa ] [pa
1
]
-символи Ґаусса після першого перетворення вихідної системи (5.22).
Аналогічно поступаємо з системою рівнянь (5.24), тобто перше рі
поділимо на [pb
2
A] Ф 0, після чого матимемо
т
2 + ГТГ7Г
•
&Р
Ьс
- Ч
т
з + [pbd.
1]т
4
+ [pbl.
1]}
= 0. (!
[pb .1]
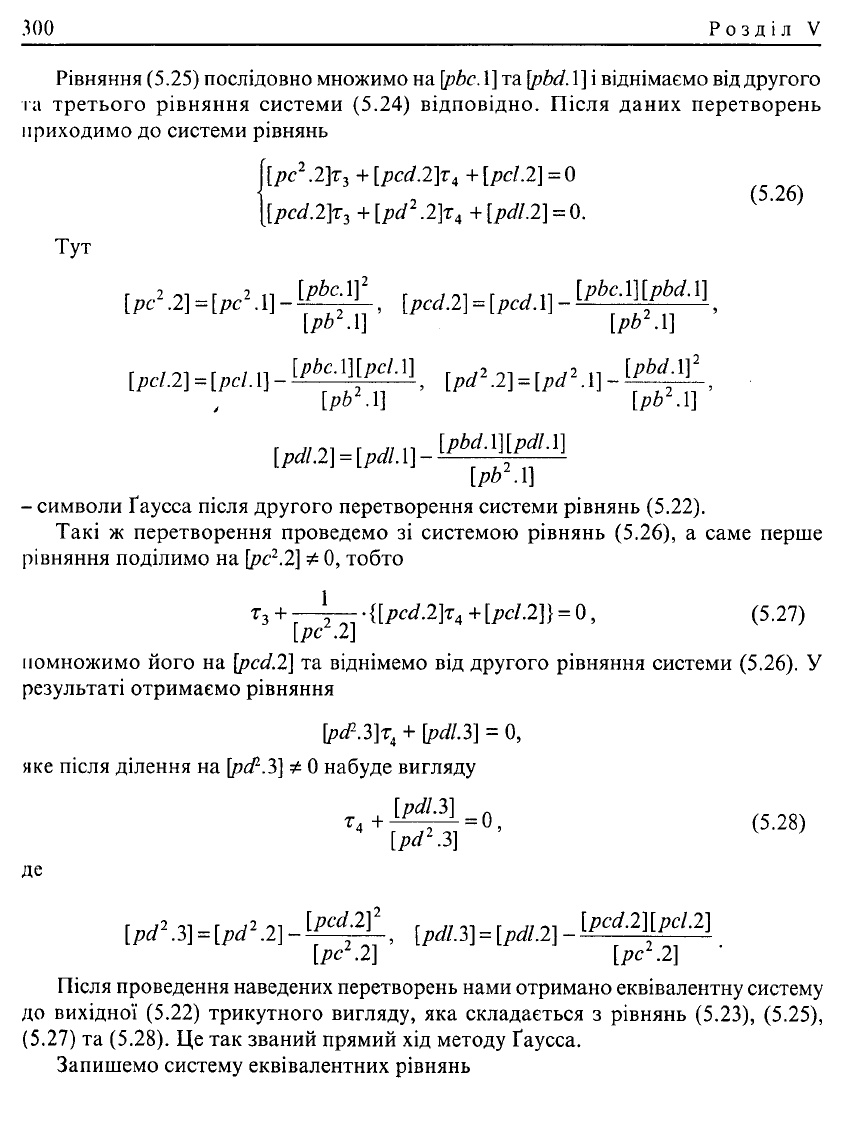
300
Розділ V
Рівняння (5.25) послідовно множимо на \pbc.
1]
та \pbdA] і віднімаємо від другого
та третього рівняння системи (5.24) відповідно. Після даних перетворень
приходимо до системи рівнянь
\[рс
2
,2]т
3
+ [pcd. 2]т
4
+ [реї.2] = 0
\[pcd.2]r
3
+ [pd
2
.2]т
4
+ [pdl.2] = 0.
Тут
IpS.2]-[рс>.1]-I^lll, [pcd.2].[pcrf.l]-І^У ,
[/76 .1] .1]
Г /П Г /11 [рЬс.ЩреІА] 2 г J2 11 [рМ.І]
2
[/»с/.2] = [/7с/.
1]
, [/>rf .2]-[pd .1]- ,
[pb .1] [pb .1]
[pdl.2] = [pdl.l}-
[pbdA]
l
pdlA]
[pb
2
.1]
- символи Ґаусса після другого перетворення системи рівнянь (5.22).
Такі ж перетворення проведемо зі системою рівнянь (5.26), а саме перше
рівняння поділимо на \рс
2
.2]
Ф
0, тобто
т
3
+ -4—
•
{[pcd.2]т
4
+ [реї.2]} = 0, (5.27)
[рс .2]
помножимо його на [pcd.2] та віднімемо від другого рівняння системи (5.26). У
результаті отримаємо рівняння
[рсР.З]г
4
+ [pdl. 3] = 0,
яке після ділення на [pd
1
.3]
Ф
0 набуде вигляду
[pd
2
.3]
де
[pd
2
.3] = [pd
2
.2] -
[pcd
;
2]2
, [pdl. 3] = [pdl.2] -
[pc
2
.2] [pc .2] •
Після проведення наведених перетворень нами отримано еквівалентну систему
до вихідної (5.22) трикутного вигляду, яка складається з рівнянь (5.23), (5.25),
(5.27) та (5.28). Це так званий прямий хід методу Ґаусса.
Запишемо систему еквівалентних рівнянь

Методи врівноваження багатьох виміряних величин
Т, +"
[ра
2
]
Т
2
+
•
{[pab]т
2
+ [рас]г
г
+ [pad]т
4
+ [раї]} -
О
•
{[pbc.
1]т
3
+ [pbd. 1]т
4
+ [pbl.
1]}
=
О
1
[pb
2
.1]
(5.2
т, +-
[рс
2
.2]
•{[/7^.2]т
4
+[рс/.2]} = 0
[^.з]
Проведемо зворотній хід методу Ґаусса, а саме, розв'яжемо систему рівь
(5.29), починаючи з останнього рівняння
7Г
3
=-
т
2
=-
[pdl. 3]
[pj
2
.3]
1
[р
С
2
.2]'
1
[Pb
2
.1]'
{[ра/.2]т
4
+ Lpc/.2]}
(5.:
Ті ="
[ра
•{[/?а&]т
2
+ [рас]т
і
+[pad]r
4
+[pal]}.
Рівняння (5.30) називаються елімінаційними, з яких визначаються попрг
т,.(у = Ї4).
5.4.2. Метод оберненої матриці
Розглянемо матричне нормальне рівняння поправок (5.21)
NT+ 5 = 0, (5.:
де N =
А
Т
РА, В = A
T
PL.
Припустимо, що визначник матриці N не дорівнює нулеві, тобто
|7V|
= detA
Тоді існує обернена матриця Q =
N~
]
до матриці N.
Рівняння (5.31) помножимо на матрицю Q, після чого отримаємо
QNr+ QB = 0.
Оскільки QN = NQ = Е - одинична матриця, то

302
Розділ V
т
+ QB
=
0, або т
=
—QB.
(5.32)
Таким чином, із виразу (5.32) можна визначити невідомий вектор поправок.
Обернена матриця Q до матриці TV знаходиться за відомим правилом, поданим
у розділі І. Але її можна знайти і за методом Ґаусса.
Запишемо матрицю N для чотирьох рівнянь. Це буде матриця коефіцієнтів
системи (5.22).
ґ ") \
[pa
]
[pab] [рас] [pad]
[pab][pb
2
][pbc][pbd]
[рас] [pbc] [pc
2
][pcd]
[pad] [pbd] [pcd] [pd
2
]
ч У
Для знаходження оберненої матриці Q використаємо тотожність N Q = Е, яку
запишемо у розгорнутому вигляді
N =
(5.33)
[pa
]
[pab] [рас] [pad]
[pab][pb
2
][pbc] [pbd]
[рас] [pbc] [pc
2
]
[pcd]
[pad] [pbd] [pcd] [pd
2
]
#11 #12 #13 #14
q2i
q22
Я
23
424
#31 #32 #33 #34
#41 #42 #43 #44
'1000"
0100
0010
0001
V У
Після проведення множення матриць N та Q одержимо чотири системи
лінійних алгебраїчних рівнянь для знаходження невідомих елементів q
tj
(і, j = 1,4)
матриці Q
N-
Розв'язавши наведені системи рівнянь, матриці коефіцієнтів яких є однаковими
(матриця N), отримаємо шукану матрицю Q. Слід відзначити, що вона, як і
матриця N, буде симетричною.
'#11"
гг
/ \
#12
f
0
l
'#14 "
0
#21
#31
=
0
0
, N-
#22
#32
-
1
0
, N-
#23
#33
=
0
1
, N
•
#24
#34
0
0
0
v У
,#42;
0
V У
ч
#43
J
0
V У
,#44 j
1
V У
5.4.3. Метод квадратних коренів
Одним із ефективних методів розв'язування нормальних систем лінійних
алгебраїчних рівнянь є метод квадратних коренів.
