Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи теорії похибок вимірювань 281

— = х

Pf М

дх,

1 « - 1 1

— = laf—,або p

=f~p\

о РІ <'

РІ

Якщо вагир.(і -\,п) виміряних величин х. є однаковими, тобтор.-р

= ...

•

1 [я

] « Р

— = і , або p

=—5".

Р W]

Слід зауважити, що для величин и = х + у та v = х-у вагир

ір

є однак

РхРу

Рг,

Px+Pv

Дана рівність випливає з результату підстановки виразів часткових по

ди ди , dv dv , , ,

для величин и IV, — = — = 1, — = — = -1 у формулу (4.65).

дх ду дх ду

3 1 2

Приклад 1. Обчислити вагу функції и =

—

х —у+ —z, якщо ваги арг>

4 6 5

х, у, z є такими: р

= 4; р

= 2;р. = 6.

Знайдемо часткові похідні функції и = и(х, у, z)

ди _ 3 ди 1 ди _ 2

4' ду 6 ' dz 5

Використавши формулу (4.65), отримаємо значення ваги для функції

= і

_1_

л2

• +

' г

1 (2^

1914

п,о,

•- = — + — + — = 0,181;

6 64 72 150

~ 5,519.

Приклад 2. Визначити вагуp

суми кутів трикутника, якщо виміряно двг

та

з однаковою точністю.

Третій кут у

трикутнику функціонально виражається через кути а т;

7= 180-а-Д

Приймаючи ваги кутів а та

такими, що дорівнюють одиниці, за фо{

(3,65) знайдемо вагу кута у, врахувавши, що — = — = -1,

да др

282

Розділ IV

Ру 1 1 ' 2

Суму кутів трикутника S можна подати як функцію кутів а, Д утак:

S = а +

+ у.

35* dS

Оскільки — = — = — = 1, то, застосувавши формулу (4.65), знайдемо вагу

da д(3 dy

суми кутів трикутника — = І

•

- +1

•

- +1

- —

+ 2 = 4, або Ps

~ .

1 1

Приклад 3. Кут а у трикутнику визначено п'ятьма прийомами, а кути

та у

і рьома та чотирма, відповідно. Визначити вагу суми кутів трикутника. За

одиницю прийняти вагу кута, виміряного одним прийомом .

г-. , п . • dS dS dS , 111

Оскільки S= a + у, і —- = — = — =

та^„=-, p

=~, p

=- то,

да ар ay 5 3 4

* ™ 1 1 1 1 47 . 60

ішкориставши формулу (4.65), отримаємо — = _ + _ + _ = — звідки p

= — .

5 3 4 60 47

§ 4.21. Визначення середньої квадратичної похибки одиниці ваги

з ряду парних нерівноточних вимірювань

Розглянемо ряд результатів парних вимірювань однорідних величин

/,',/," (і = \,п),

ірипустивши, що окремі вимірювання в парі є рівноточними, але вимірювання в

*)ізних парах - нерівноточні з вагами p..

Розглянемо різниці dj =l'j-lі (і- \,п). Оскільки ваги вимірювань І', та І" є

однаковими та рівними p., то згідно формули (4.65) або зауваження (2) із парагра-

фу 4.20, вага різниці d. буде дорівнювати .

Так як величини d. (і = 1,п) є своїми істинними похибками, то для визначення

:ередньої квадратичної похибки /л одиниці ваги застосовуємо формулу (4.57). У

результаті отримаємо

Елементи теорії похибок вимірювань

283

Якщо ваги результатів вимірювань у одній парі будуть різними та рівними р', р

то вагу z'-ої різниці можна визначити за формулою (див. Зауваження 2, §4.20)

/ №

У випадку наявності систематичних похибок у різницях результатів парні

вимірювань, їх спочатку усувають, тобто, якщо d. (і = 1,и) є систематичню

похибками окремих різниць, то величини Ad. = d. - 8. можна вважати СВОЇЇ

надійними похибками з вагами "у. Тоді, використавши формулу (4.6!

отримаємо вираз для знаходження середньої квадратичної похибки одиниці ва

[pAd

]

"-ЦЬ^У

Отже, формула (4.67) дає можливість визначити середню квадратичну похиЄ

одиниці ваги з результатів парних нерівноточних вимірювань при наявност

різницях систематичних похибок.

§ 4.22. Опрацювання результатів нерівноточних вимірювань

При опрацюванні ряду нерівноточних вимірювань

І.

(і = 1 ,п) якоїсь величи

істинне значення якої є невідомим, потрібно

1) обчислити надійне значення вимірюваної величини, яким буде сере;

арифметичне результатів спостережень за вагами

0 -

г і '

[Р\

а якщо кількість вимірювань п є достатньо великою, то

L -I +М

М)

'о

г л

[р]

де /

- наближене значення вимірюваної величини (як правило, приймаї

мінімальне значення вимірюваної величини);

є.

= / -/

(і -1,п) - остачі (відхиле

виміряних значень від наближеного);

2) знайти середню квадратичну похибку одиниці ваги за формулою (4.62'

ї я-1

286

Розділ IV

здійснюючи контроль обчислень співвідношенням jX = . Тут Я - коефіцієнт

пропорційності, прийнятий при встановленні ваг вимірювань; <5. = /. - L

або

8 j =£,--—,/ = 1,п;

3) визначити оцінку точності Мсереднього вагового L за таким співвідношенням:

М = • "

М'

Розглянемо ряд результатів парних вимірювань однорідних величин

Я',Я" (і-\,п), із вагами р\, р" відповідно.

Математичне опрацювання рядів парних нерівноточних вимірювань зводиться

до знаходження оцінок.точності. Для цього потрібно

1) обчислити різниці dj = І'і-І" (і = 1 ,п) і знайти відповідні їм ваги за формулою

_ _ Рі'Рі . 7-.

-—Г,—і = 1,и>

РІ+РІ

2) перевірити виконання нерівності

|[^]|<0,25-[|^|], (4.68)

яка свідчить про відсутність систематичних похибок у різницях результатів

вимірювань;

3) у цьому випадку середня квадратична похибка одиниці ваги обчислюється

за формулою

V п

Якщо ж нерівність (4.68) не виконується, тобто різниці d. (і~\,п) містять

систематичні похибки, то спочатку обчислюють виправлені різниці d\, усунувши

[pd]

середній залишковии систематичнии вплив

[р]

' ' [р]

і, вважаючи їх відхиленням від середнього вагового, середню квадратичну похибку

одиниці ваги знаходять за формулою

lJd

V п -1

Елементи теорії похибок вимірювань 285

Точність середнього вагового значення з кожної пари вимірювань оцінюс

таким співвідношенням:

Ц . , _

mj = , і=\,п.

Зауваження. Наведений підхід врахування впливу систематичних похі

приводить, як правило, до отримання завищеної оцінки середньої квадрати

похибки одиниці ваги. Тому доцільніше усувати систематичний вплив, вихо,

з умов конкретної задачі. Наприклад, при опрацюванні результатів геометрич

нівелювання виправленими різницями будуть величини

< = 4-їй-*'

[к]

де — - коефіцієнт систематичного впливу; к. - кількість штативів г'-ої секц

[к]

Якщо проводиться опрацювання результатів лінійних вимірюва

полігонометрії, то виправлені різниці обчислюють за формулою

Тут коефіцієнтом систематичного впливу є величина

;

S -довжина г-ої

§ 4.23. Приклади опрацювання нерівноточних вимірювань

Приклад 1. Для визначення висоти вузлової точки А від шести ре

прокладено нівелірні ходи. Знайдено висоти точки за кожним ходом

(і = 1

їх середні квадратичні похибки т. (і - 1,6). Потрібно знайти надійне зна

висоти точки А та її середню квадратичну похибку.

У таблиці 4.5 наведено всі необхідні дані для опрацювання.

Запишемо контрольне співвідношення

[р8

\ = [рє

3338,47-

212

842

= 3338,47-2826,36 = 512,11

[р] 16,04

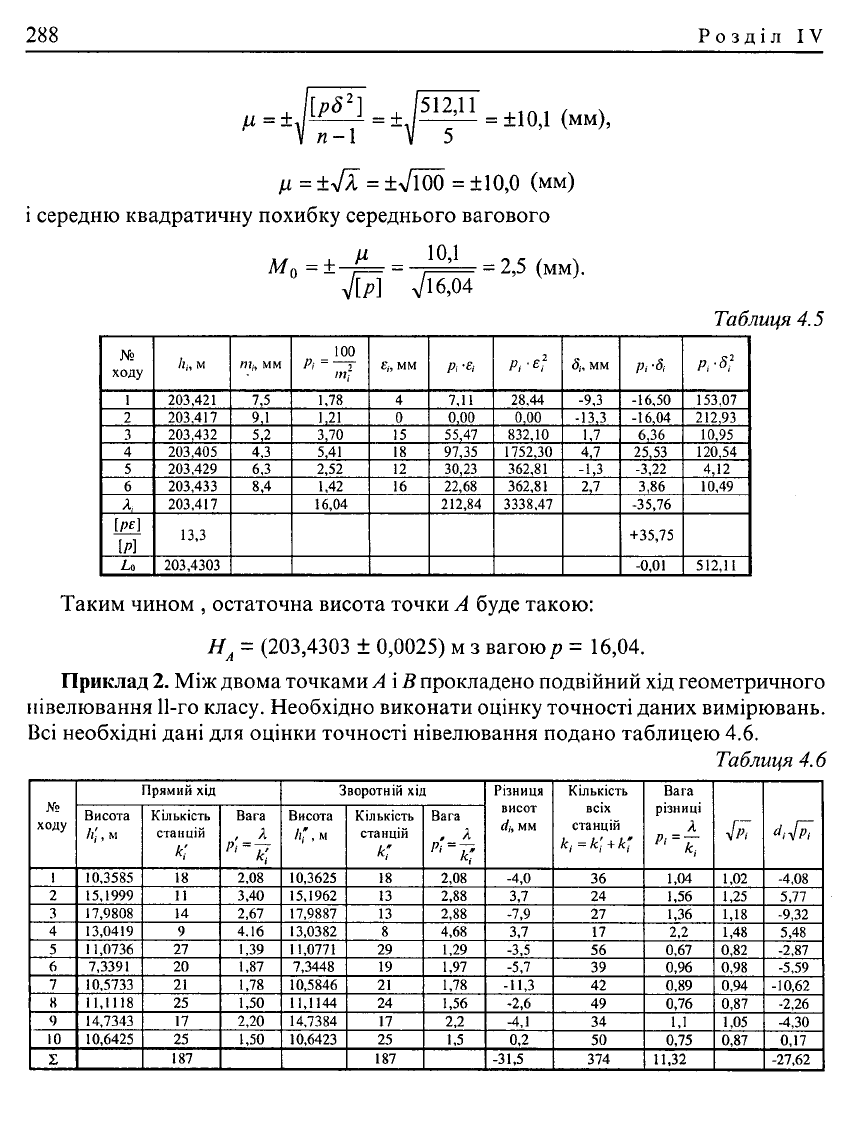
та обчислимо середню квадратичну похибку одиниці ваги

288

Розділ IV

И = ±у[х = ±VlOO = ±10,0 (мм)

і середню квадратичну похибку середнього вагового

= ±-jL= = Z

0,1

= 2,5 (мм).

<J[p] М04

Таблиця 4.5

№

ходу

Лі, м

Лї„ ММ

100

Рі = —т

£,, ММ

РІ 'Є:

л-е,

5„ мм

PrS, P.Sf

1 203,421 7,5 1,78 4

7,11

28,44 -9,3 -16,50 153.07

2 203,417 9,1

1,21

0 0,00 0,00 -13,3 -16,04 212,93

3 203,432 5,2 3,70 15 55,47 832.10 1,7 6,36 10,95

4 203,405 4,3 5,41 18 97,35 1752,30

4,7 25,53

120,54

5 203,429 6,3 2,52 12 30,23 362,81

-1,3

-3,22 4,12

6 203,433 8,4 1,42 16 22,68 362,81 2,7 3,86 10,49

я,

203,417

16,04

212,84 3338,47 -35,76

\ре]

ІР]

13,3 +35,75

203,4303 -0,01 512,11

Таким чином , остаточна висота точки А буде такою:

= (203,4303 ± 0,0025) м з вагою р = 16,04.

Приклад 2. Між двома точками Л і В прокладено подвійний хід геометричного

нівелювання 11-го класу. Необхідно виконати оцінку точності даних вимірювань.

Всі необхідні дані для оцінки точності нівелювання подано таблицею 4.6.

Таблиця 4.6

№

ходу

Прямий хід Зворотній хід Різниця

висот

d„

мм

Кількість

всіх

станцій

к, = к\

+ к"

Вага

різниці

4Ї,

d,JPi

№

ходу

Висота

ІІ'і , м

Кількість

станцій

к;

Вага

, я

Рі =

Висота

h",

Кількість

станцій

к"

Вага

, я

Різниця

висот

d„

мм

Кількість

всіх

станцій

к, = к\

+ к"

Вага

різниці

4Ї,

d,JPi

10,3585 18 2,08 10,3625 18

2,08 -4,0 36 1,04 1,02

-4,08

2 15,1999 11

3,40 15,1962 13 2,88

3,7

1,56 1,25 5,77

3 17,9808

2,67

17,9887 13 2,88 -7,9 27

1,36 1,18 -9,32

4 13,0419

9 4.16 13,0382 8 4,68

3,7 17 2,2

1,48 5,48

5 11,0736 27 1,39 11,0771 29

1,29 -3,5 56 0,67 0,82

-2,87

6 7,3391 20 1,87

7,3448 19 1,97 -5,7

39 0,96 0,98 -5,59

10,5733

1,78 10,5846 21 1,78

-11,3 42 0,89 0,94

-10,62

11,1118 25 1,50 11,1144 24

1,56 -2,6

49 0,76 0,87 -2,26

9 14,7343

17 2,20

14,7384

17 2,2

-4,1

1,1

1,05 -4,30

10 10,6425 25 1,50

10,6423 25 1,5 0,2 50

0,75 0,87 0,17

187

187 -31,5 374

11,32 -27,62

Елементи теорії похибок вимірювань 287

Виберемо ваговий коефіцієнт

10 10

Сума різниць [d\ = -31,5 свідчить про наявність у них систематичних пол

що і підтверджує невиконання нерівності (4.68)

[| dyfp |] = 50,46,

I[djp]

|= 27,62,27,62 > 0,25-50,46 = 12,62.

Усунемо систематичні похибки через середній залишковий систематі

вплив і за кількістю станцій. Для цього побудуємо таблицю 4.7.

Тиблі

№

ходу

di,

мм

Усунення середньої

залишкової

систематичної похибки

Усунення систематичної похибки

за кількістю станцій

№

ходу

di,

мм

d,p,

d'i

М'

Pidt

[*1

/v/;

1 .

-4.0

1,04

-4,16

-1,75

-1,82

3,18

-2,88

-1,12

-1,16

1,30

2 3,7

1,56

5,77

5,95 9,28

55,22

-1,92

5,62

8,77

49,29

3 -7,9 1,36

-10,98

-5,65

-7,85

44,35

-2,16 -5,74

-7,81

44,83

4 3,7

2,2

8,14

5,95

13,09

77,89

-1,36

5,06

11,13

56,32

-3,5

0,67 -2,45

-1,25

-0,84

1,05

-4,48

0,98

0,66

0,65

-5,7 0,96

-5,47

-3,45

-3,31

11,42

-3,12

-2,58

-2,48

6,40

-11,3

0,89

-10,06

-9,05

-8.05

72,85

-3,36 -7,94

-7,07

56,14

-2,6 0.76

-1,98

-0,35

-0,27

0,10 -3,92

1,32

1,00

1,32

-4,1

1.1

-4,51

-1,85 -2,04

3,77 -2,72

-1,38

-1,52

2,10

0.2 0,75

0.15

2,45

1,84

4,51

-4,00

4,2

3,15

13,23

£ -31,5

11,32 -25,45

274,34

-29,92

0,00

231,58

Обчислимо залишковий систематичний вплив

= = -2,25 (\

[Р] 1U2 *

коефіцієнт систематичного впливу — = - їм = -0,08 мм. Після цього зна

[к] 374

середню квадратичну похибку одиниці ваги fx та середню квадратичну пс

нівелювання на одній станції т у випадку залишкового систематичного і

~ЛІ

274,34

= ±5,52 (мм), Т = ± -^L = ± = ±0,9 (мм), та за кількістю с

V 9

УІ2 Щ4

= ±

аР^

= ±5

072

(

мм

= = ±0,829 (мм).

V 9

л/37^4

РОЗДІЛ V

МЕТОДИ ВРІВНОВАЖЕННЯ

БАГАТЬОХ ВИМІРЯНИХ

ВЕЛИЧИН

§ 5Л. Суть задачі врівноваження декількох виміряних величин

У теорії похибок вимірювань подано методику опрацювання вимірювань однієї

величини. Але в реальних геодезичних задачах завжди вимірюється не одна, а кілька

величин, серед яких є необхідні та надлишкові. Наявність надлишкових вимірювань

є обов'язковою, оскільки завдяки їм підвищується точність вимірюваних величин і у

зв'язку з цим вони стають пов'язаними певними математичними співвідношеннями.

Наприклад, виміряно три кути плоского трикутника. Сума виміряних кутів

повинна дорівнювати 180°. Достатньо виміряти два кути а та/З трикутника, а

третій кут / знайти зі співвідношення у= 180° - а- /3. Оскільки виміряно і третій

кут у, то повинна виконуватись умова, що сума кутів трикутника дорівнює 180°.

У зв'язку з цим появляються нев'язки (умова виконуватись строго не буде), які

дають змогу надійно контролювати вимірювання та виявляти грубі похибки. З

іншого боку нев'язки потрібно усунути за рахунок внесення поправок до

результатів вимірювань, отримавши нові (врівноважені) надійні значення

виміряних величин. Знаходження надійних значень виміряних величин при

сумісному опрацюванні вимірювань називається врівноваженням.

Сформулюємо задачу сумісного врівноваження багатьох виміряних величин.

Для цього розглянемо п виміряних величин х. (і =

п) із вагамир. (і =

п), істинні

значення яких є X. (і-\,п). Зі змісту задачі відомо, що виміряні величини

х. (і -1 ,п) пов'язані між собою співвідношеннями

<р.(х,,х

, ...,х

), j = \,Г. (5.1)

Серед рівнянь (5.1), яким повинні задовільняти результати вимірювань, можуть

бути залежні між собою рівності. їх не розглядатимемо. Вважаємо, що всі

співвідношення (5.1) є незалежними. При появі в результатах вимірювань окремої

Методи врівноваження багатьох виміряних величин

надлишково виміряної величини з'являється і окрема незалежна умова

кількість рівнянь г системи (5.1) дорівнює кількості надлишкових вим

величин. У цьому випадку завжди виконуватиметься нерівність г < п, ос

надлишкові виміряні величини є підмножиною множини всіх виміряних ве.

Таким чином, система рівнянь (5.1) є недовизначеною (кількість рівнянь є

м<

за кількість невідомих), а отже, має нескінчену множину розв'язків. Ріі

системи (5.1) називаються умовними рівняннями.

Оскільки результати вимірювань х. (і = 1 ,п) отримано з деякими похиі

то в результаті підстановки їх у систему рівнянь (5.1), одержимо

(pf.x

, ...,х

) = W., j -\,г.

де Wj

= \,r) - нев'язки, які не дорівнюють нулеві.

Тому задача врівноваження зводиться до усунення нев'язок W

У <

рівнянь (5.2), для чого потрібно знайти поправки v. (і = \,п) до резуі

вимірювань х. (/ = 1,и). Підставивши у систему рівнянь (5.2) замість х. (

виправлені значення х. + v. (і =

п), або врівноважені значення виміряних вс

прийдемо до такої недовизначеної системи рівнянь:

ф.(х, + v

+ v

, ..., х

+ v

) = 0, j = 1 ,r.

Система рівнянь (5.3) має нескінчену множину розв'язків, тому сер

потрібно знайти найкращий розв'язок у тому сенсі, щоб введені поправки

н<

усунули нев'язки в системі умовних рівнянь, але й максимально наб

поправки за абсолютною величиною до істиних похибок. Якщо по

дорівнювали б істинним похибкам результатів вимірювань за абсол

величиною та були б протилежними за знаком, то це був би ідеальний рс

системи рівнянь (5.3). Але на жаль, його практично отримати неможлив<

Єдиний розв'язок системи (5.3) можна знайти, довизначивши її якимось

У більшості випадків і, зокрема, в геодезії систему рівнянь (5.3) розв'я:

використанням методу найменших квадратів, тобто розв'язок системи (5.3) \

таким, щоб сума квадратів поправок для рівноточних вимірювань була мінім

" 2 2

] min

1=1

або, щоб сума добутків відповідної ваги на квадрат поправки для нерівне

вимірювань була мінімальною

—>

min.

/=і

292

Розділ V

Метод найменших квадратів дозволяє знайти єдиний розв'язок системи (5.3),

причому він усуває появу великих поправок і для рівноточних вимірювань

поправки рівномірно розподіляються між результатами вимірювань, а для

нерівноточних вимірювань ваги р. (і = \,п) зменшують поправки v. (і' = 1,и)

до точніших результатів вимірювань і збільшують їх до менш точних

результатів.

До переваг методу найменших квадратів слід віднести його загальність та

простоту обчислень на відміну від інших методів врівноваження.

Отже, сумісне врівноваження вимірюваних величин із використанням методу

найменших квадратів є задачею на умовний екстремум, тобто потрібно знайти

мінімум функції F =[pv

], де змінні v. (і = 1,«) пов'язані незалежними умовними

рівняннями (5.3).

Наведену задачу розв'язують двома шляхами. Перший полягає у знаходженні

абсолютного екстремуму функції F-\pv

], де всі виміряні величини подаються у

вигляді функцій від деяких незалежних і невідомих величин (параметрів). Даний

підхід називається параметричним методом.

Другий шлях полягає у заходженні умовного екстремуму функції F =\pv

} із

використанням методу Лагранжа, де фігурують невизначені множники (у геодезії

їх називають корелатами). Цей підхід називають корелатним методом.

Обидва методи є еквівалентними, тобто вони є тільки різними підходами

розв'язування однієї і тієї ж задачі.

§ 5.2. Основи параметричного методу врівноваження

Розглянемо результати виміряних величин, істинні значення яких дорівнюють

•V. (/' = 1,л). Припустимо, що їх виміряні значення х (і = 1 ,п) отримано з вагами

(і = \,п), причому серед них є к необхідних і г надлишкових. Виберемо к

незалежних параметрів (у якості параметрів можна взяти необхідні виміряні або

певиміряні величини), істині значення яких позначимо через Т. (j = 1Д). Істинні

значення виміряних величин X. (/ = 1,и) функціонально подамо через істині

значення параметрів Т (j = 1,к) у вигляді

X=f

,...,T

),i = ЇЯ (5.6)

Розглянемо врівноважені значення t. (j = 1 ,к) невідомих параметрів Т. (j = 1 ,к)

і праві та ліві частини рівностей (5.6) запишемо для врівноважених значень