Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.

Методи врівноваження багатьох виміряних величин
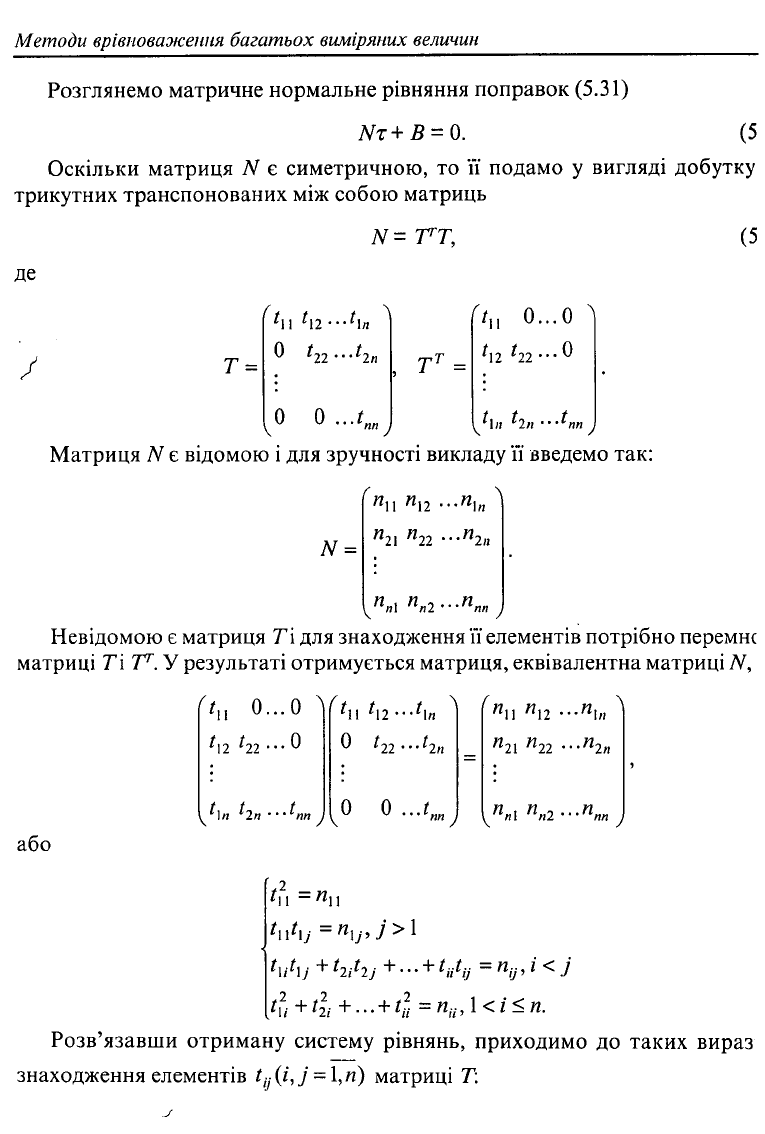
Розглянемо матричне нормальне рівняння поправок (5.31)
Nz+B = 0.
(5
Оскільки матриця N є симетричною, то її подамо у вигляді добутку
трикутних транспонованих між собою матриць
N= ТТ,
(5
де
/
Т =
Ґ
і t t
4
Ml
12
•••'in
0 ti2---hn
v
0 0 ...t
nn
T =
0...0
?22
"
*
^
^2n •••^nn
j
Матриця N є відомою і для зручності викладу її введемо так:
N =
«11 «12
«2. «22 -»2п
Невідомою є матриця Гі для знаходження її елементів потрібно перемне
матриці Ті
Г
7
".
У результаті отримується матриця, еквівалентна матриці N,
t
u
0...0
/,2
t22
••• 0
hn
• • -tnn
j
t
n
t
n
...t
1 n
t
22
•••t
2n
0 ...t„
n
xx
n
x2
l%2\
ft22
* * 'ft
2 n
n , n
~
...n
у nl n2
nn
у
або
^ii ~
n
\\
hihj =n
XJ
,j>\
t
u
t
Xj
+t
2l
t
2j
+ ... + t
a
t
y
= n
ip
i<j
t
Xi
+t
2
2i
+... + tl=n
H
,\<i<n.
Розв'язавши отриману систему рівнянь, приходимо до таких вираз
знаходження елементів ty(i,j = \,n) матриці Т\

304
Розділ V
'п -v"її»
П
І І
t
u
=-±J>
1,
МІ
(5.36)
'я =
Л
К -
і-і
n
ij ~ ^kihj
t
0
= р ,і<Л
Матричне нормальне рівняння поправок (5.34) із врахуванням рівності (5.35)
є еквівалентним системі двох матричних рівнянь
які запишемо в розгорнутому вигляді
t\\
x
\ -
t\2
X
\
*22
Х
2
~ ^2
hn
x
\ +hn
X
2 +
•••
+
*,т
Х
п
- t-
(5.37)
1
T
1
+t
i2
T
2 +
• • •
+ t
ia
r„ ~
X
1
(22^2
+
• • •
+
to,,?»
=
X
7 2n
L
n
t T = X .
nn n n
(5.38)
Розв'язавши системи лінійних алгебраїчних рівнянь (5.37) та (5.38), отримаємо
такі вирази:
Ь,
х, =•
X: =•
til
1-1
b
t
+ li
ki
x
k
^ ,
1
<і<п
hi
(5.39)

Методи врівноваження багатьох виміряних величин
X
" t
Х
і ~ X tjk
r
k
*=і±! \<і
<п
.
Л,-
У процесі практичних обчислень слід дотримуватись такої послідовне
спочатку знайти елементи ty(i,j = l,n) матриці Гта хД/ = 1,п) за формулами (і
і (5.39), що є прямим ходом обчислень методу, після чого здійснити зворотнії
- обчислити поправки тДі = 1 ,п) за формулами (5.40).
5.4.4. Метод ортогопалізацїї
Не менш ефективним методом розв'язування нормальних систем ліній
алгебраїчних рівнянь є метод ортогоналізації. Припустимо, що матриц
матричного нормального рівняння поправок (5.31) є стійкою, тобто малим змі
елементів матриці N відповідають малі зміни елементів її оберненої матриці
а значить матричне рівняння поправок (5.31) є добре обумовленим.
Розв'язок рівняння
Nt=-B, (5 А
де det/V* 0, шукатимемо у вигляді
к ...
т = Еа
<
т
10
. (5.4
і=і
Тут т =(т
р
т
2
, ..., т
к
)
Т
- шуканий вектор поправок; а. - невідомі коефіціе
розкладу; т
(,)
=(т
1
(
'
)
,т^'
)
,...,г['
)
)
г
- невідомі лінійно незалежні вектори.
Вимагатимемо, щоб вектори т
и)
(і - 1,/с) задовільняли умови ортогонально
Г
(.І)Т .
Nt
U)
= 0>
ij
= (5 А
Зображення вектора поправок (5.42) підставимо у матричне нормал
рівняння поправок (5.41). У результаті отримаємо
к
т
(п
=-В.
;=1
Отримане співвідношення помножимо на вектор т
U)T
(j = 1 ,к)

306
Розділ V
Іа,.т
и)г
-Nz^ =-z
U)T
В
і=і
і, врахувавши умови ортогональності (5.43), одержимо
А/V
U)T
-NT
U)
=-T
U)T
В,
звідки знайдемо коефіцієнти розкладу а
;
(j = к) вектора поправок т
т
и)Т
В
"/=- rnr „ (5.44)
т
Розглянемо систему лінійно незалежних векторів
?
(1)
=(1Д...,0)
Г
,
t
(2)
=(0,1,...,О)
7
",
t
(k)
=(0,0,...,1)
т
,
за допомогою якої побудуємо систему векторів т
(/)
(у' = 1 ,к) так:
г
(1)
=/
(1)
,
т
(2)
=t
(2)
+ Л
2
т
0)
,
Аг—1
(5.45)
Коефіцієнти А«
У
=
1,Л: — 1, 1
= 2,к знайдемо, використавши умови ортого-
нальності (5.43).
Для знаходження коефіцієнта Л
{2)
використаємо рівність ^•
X)T
-NTP-
)
= 0, або,
підставивши сюда друге рівняння зі співвідношень (5.45), отримаємо
Т
(1)Г
-М
(2)
+А
(
Д
(,)Г
-АТ
(1)
=0,
звідки
Т
(1 )Т ,
Ш
(2)
я<
2
>=-
Запишемо третє рівняння зі співвідношень (5.45), тобто Т
(3)
= t
(i)
+ Я
(
,
3)
т
(1)
+Я
(
2
3)
Т
(2)
.
Для знаходження коефіцієнтів Я'
3)
і Я
(
2
3)
поступаємо аналогічно попередньому випадку,
а саме, використавши рівності

Методи врівноваження багатьох виміряних величин
з)
= = 0j
одержимо вирази для знаходження коефіцієнтів Я]
3)
, Я
(
2
3)
Т
(1)Г
-М
(3)
+Я5
3)
Т
(1)Г
-АТ
(1)
=0,
т
<2)7
" -Nt
(i)
+Я
(
2
3)
Т
(2)Г
-7VT
(2)
= 0,
Т
(1)Г . дгЛЗ)
1
т
(1)г
-^т
(1)
'
(3)=
т
(2)Г
-М
(3)
T
{2)T
-NT
(2)
'
Продовжуючи даний процес, можна обчислити всі коефіцієнти
j = hk
1 = 2,к, які дають можливість визначити систему лінійно незалежних векті
(5.45). За допомогою даної системи векторів із використанням формули (f
отримуються коефіцієнти розкладу a j(j = 1 ,к) вектора поправок т. Підстави
знайдені значення коефіцієнтів (Xj(j = l,k) у співвідношення (5.42), одерж
шуканий вектор поправок т=(т
р
т
2
, ...,
5.4.5. Метод простої ітерації
Наведені раніше методи розв'язування нормальних систем ліній
алгебраїчних рівнянь є точними, тобто якщо коефіцієнти системи та вільні 4J
є точно задані, то при проведенні обчислень без заокруглень можна отрт
точний розв'язок. Але на практиці приходиться розв'язувати нормальні сисі
лінійних алгебраїчних рівнянь, коли кількість їх є досить великою,
розв'язування їх стає незручно використовувати точні методи, оскільки
проводити громіздкі обчислення. У зв'язку з цим застосовують наближені меі
розв'язування, які є зручними для застосування комп'ютерних технологій, о
яких наведемо метод простої ітерації та метод Зейделя.
Розглянемо матричне нормальне рівняння поправок (5.31). Оскії
діагональні елементи матриці N є нерівними нулеві, то перший рядок матриї
і В поділимо на
[а
2
р],
другий - на
[Ь
2
р]
і т.д., &-ий - на [и
2
р\ і визначимо з пери
рівняння нормальної системи поправку т
р
з другого рівняння - поправку т
2
і
із к-то рівняння - поправку
т
к
.
У результаті отримаємо зведену систему ріві
поправок

308
Розділ V
т, = - —Ц
•
([pal] + [pab] т
2
+... + [раи]т
к
)
[ра~]
1
[pb
2
]
•
dpbl] +
[раЬ]т
х
+... + [pbu]x
k
)
•
([pul] + [раи]т, +... +
[/JVMJT^.,
).
(5.46)
Систему рівнянь (5.46) будемо розв'язувати методом послідовних наближень.
За нульове наближення розв'язку системи (5.46) виберемо стовбець вільних
членів, тобто
.(0)
т
(0) _
ь і,
—
[раї]
[ра
2
]
[рЬЦ
[pb
2
]
[ри[[
[ри
2
]
(5.47)
Тоді перше наближення розв'язку системи (5.46) на основі нульового
будуємо так:
т<»=--
[ра
2
]
([раї] + [раЬ]т^ +... + [рай] т[
0)
)
(0)>
4
П
=-—гЛР
ЬІ
] + [раЬ]т?
)
+ ... + [рЬи]т™)
г(І)
[pb
2
]
[ри
2
]
([pul] + [раи]т^ +... + [pvu]r
{
k
°_\).
(0)
На основі цього довільне наближення розв'язку можна записати

Методи врівноваження багатьох виміряних величин
г(") _.
1
ТГ =
тт'
(М + W" + ... + [рай] т^)
Т
2
-
[ра
2
]
1
1
(«—1) ^
([pм/] + [pйм]т
1
<л
-
1)
+ ... + [pvм]т['!.•^
1,
),
/1
= 1,2... .
Си—1) >
Якщо послідовність наближень т*
0)
, ..., ... є збіжною, тобто т =
то граничний вектор т буде шуканим розв'язком матричного норм,
рівняння поправок (5.31).
Запишемо зведену систему рівнянь поправок у матричному вигляді
де
r=B
]
-N
l
-r,
5,=
( [раї]')
/
[ра
2
]
[pbl]
[pb
2
]
> N
{
=
[pul]
{ [ри
2
]J
[pab] [рай]
[pab]
[Pb*]
0
[pbu]
'[Pb
2
]
f - \
т =
V
k
J
[pau] [pbu]
Q
[pu
2
] [pu
2
]
Тоді нульове та довільне наближення розв'язку зведеного матричного
]
поправок запишуться у вигляді
т
(0)
=Я„
г
(«)
= B
l
-N
r
T
(
"~
l
\ п = 1,2,....
Знаходження розв'язку нормальної системи лінійних алгебраїчних рівнянь
реалізованим формулами (5.47), (5.48) або (5.50) називається методом просто'
Якщо коефіцієнти матриці N
{
за абсолютною величиною є малими, то іте]
процес, визначений формулами (5.50) буде швидко збігатися, тобто для о,д
розв'язку вихідного нормального матричного рівняння поправок (5.31) із віді
точністю потрібно провести малу кількість кроків обчислень. Іншими СЛОІ

310
•Розділ V
успішного застосування методу простої ітерації діагональні елементи матриці N за
абсолютною величиною повинні значно перевищувати інші її коефіцієнти.
Оскільки збіжність ітераційного процесу залежить від коефіцієнтів матриці N
v
то не обов'язково за нульове наближення розв'язку вибирати стовбець вільних
членів. Якщо якимось чином можна визначити значення, що є близькими до
розв'язку, то вони можуть бути нульовими наближеннями.
Для збіжного ітераційного процесу важливою є властивість самовиправленості,
тобто, якщо на якомусь кроці допущено помилку, то вона не впливатиме на кінцевий
результат, оскільки помилково знайдене наближення розв'язку можна розглядати
як нове нульове наближення.
Сформулюємо достатню умову збіжності методу простої ітерації.
Теорема. Якщо для зведеної системи лінійних алгебраїчних рівнянь поправок
(5.46) сума її коефіцієнтів за абсолютною величиною у кожному рядку або стовпці
є меншою від одиниці, або для зведеного матричного рівняння поправок (5.49) сума
елементів матриці N
l
за абсолютно величиною у кожному її рядку або стовпці є
меншою від одиниці, то ітераційний процес, визначений формулами (5.47), (5.48)
або (5.50) є збіжним до єдиного розв'язку матричного нормального рівняння
поправок (5.31) для довільного вибору нульового наближення.
Наслідок. Якщо діагональні елементи матриці Ne більшими від суми всіх інших
її елементів за абсолютною величиною відповідного рядка або стовпця, то
ітераційний процес є збіжним.
5.4.6. Метод Зейделя
Даний метод є модифікацією методу простої ітерації. Ідея його полягає в тому,
що при обчисленні я-го наближення розв'язку х\
п)
враховуються вже знайдені
значення х\
п
\х
(
2
"\х\^.
Розглянемо зведену систему рівнянь поправок (5.46) та нульове наближення її
розв'язку (5.47). Перше наближення розв'язку знаходимо за формулами
т,
(1)
=-—L-([pal] + [pab]x^ +... + [раи]х^)
[ра ]
[pb
2
]
тГ =-г\-ЛриІ] + [раи]х^ +... + [pvu]xi
l
!
i
).

Методи врівноваження багатьох виміряних величин
Даний процес ітерації продовжується до тих пір, поки не буде до
відповідної точності. Отже, якщо п -
1
наближення розв'язку є відомим,
наближення отримується так:
т,
(
">
1
-{[pal} + [pab]T
(
r
X)
+... + М4"-
1
')
[ра }
А
п)
--^ггЛрЬЦ + ІраЬ}^ +... + [раи]т[
п
-
Х)
)
[pb ]
Т<"> =--\-ЛриІ] + [раи]т^ +... + MT<"_»).
[ри ]
Для методу Зейделя має місце достатня умова збіжності, яка є аналогі
і для методу простої ітерації.
За методом Зейделя отримується краща збіжність, ніж за методом просто
тільки із використанням його доводиться проводити громіздкіші обчисленн:
того, ітераційний процес, проведений за методом Зейделя буває інколи з(
тому випадку, коли він є розбіжним при використанні методу простої ітері
5.4.7. Розв'язування нормальних систем лінійних алгебраїчних рівняй
вироджених або погано обумовлених матриць
Розглянемо матричне нормальне рівняння поправок (5.31), у якому ві
матриці N є рівним нулеві або близьким до нуля.
Розв'язок такого матричного рівняння можна визначити у вигляді
т = —М
г
_
х
В,
J_
т
г
де відповідно числові ш,та матричні M
l
{
(1=\,г) коефіцієнти виражаються
фс
m]
=-Sp(N), М
0
= І,
т
2
=-^Sp(M
l
N), = М
0
•
N + т
х
І,
т
г
_, = — Sp{M
r
_
2
N), M
r
_, = M
r
_
2
•
N + т
г
_
х
І,
г-1
m
r
=--Sp(M
r
_
x
N).
г

312 Розділ V
Тут Sp(N) слід (сума діагональних елементів) матриці N; І- одинична матриця;
г - ранг матриці N.
Співвідношення M
r
_^N + тІ = 0 дає змогу судити про_похибки, що виникають
у процесі обчислень числових т,та матричних M
t
(/ = 1,г) коефіцієнтів.
Переходимо до розгляду другої частини задачі врівноваження - знаходження
оцінки точності.
Слід відзначити, що оцінка точності, виконана на основі результатів
врівноваження буде надійнішою від оцінки точності, отриманої іншими
способами, оскільки.для цього використовуються поправки до виміряних величин.
Щоб одержати оцінку точності результатів врівноваження, потрібно:
а) знайти середню квадратичну похибку одного вимірювання або середню
квадратичну похибку одиниці ваги, якщо вимірювання є нерівноточними;
б) оцінити точність наближених із точки зору геометрії геодезичної мережі
елементів за допомогою так званої вагової функції врівноважених значень, яка
складається для конкретного елемента мережі;
в) виконати оцінку точності для отриманих врівноважених параметрів.
Середня квадратична похибка т для одного рівноточного вимірювання та
середня квадратична похибка
jU
одиниці ваги для нерівноточного вимірювання
відповідно обчислюються за формулами Бесселя
деи-кількістьвимірюваньД-кількість параметрів;/?. (і = 1 ,п) -вагивиміряних величин;
§ 5.5. Оцінка точності результатів врівноваження
параметричним методом
(5.51)
або у матричному вигляді
(5.52)
/
Рх
о ... (Г
0
р
2
... о
V = v
2
- вектор поправок; Р =
діагональна матриця ваг.
