Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

Some Unsolved Problems in General Systems Theory

355

systems, Lin (1989d) proposed the following axiom: The existence of any real

matter is known by the existence of all particles in some level of the matter and

by some relations between the particles in the matter and some particles in an

environment of the matter.

As mentioned by Kunen (1980), a collection of cows cannot be considered a

set. When can a collection of objects in an application be studied as a set so that the

results in set theory and general systems theory can be used to make inferences?

Can we introduce a procedure to check when a given collection of real matter is a

“set”? Studying this question will lead to the creation of “applied set theory.”

Since a system is what is distinguished as a system, according to Klir (1985),

another difficulty we have to face to apply general systems theory is how to write

a realistic relation, such as a human relation, as one or several relations in set

theory, based upon the language of formal logic. After several systems models

have been established, do we have a procedure to select additional models so that

they produce the most desirable and most reasonable conclusions on the material

system of interest?

When faced with practical problems, new abstract mathematical theories are

developed to investigate them. At the same time, predictions based on the newly

developed theories are so “accurate” that the following question appears naturally:

Does the human way of thinking have the same structure as that of the material

world?

As shown in (Lin, 1990d), mathematics can be built upon the “empty set, Ø.”

History gradually shows that almost all natural phenomena can be described and

studied with mathematics. We thus ask: If all laws of nature could be written in

the language of mathematics, could we conclude that the universe we live in rests

on the empty set Ø, even as Genesis states that “in the beginning, God created the

heaven and the earth. And the earth was without form, and void?”

In applications of general systems theory and mathematics, it has never been

checked whether the collection of objects and the membership relation between

the objects satisfy all the ZFC axioms. Only when

∈ makes all ZFC axioms true

propositions can general systems theory and mathematics be applied to a situation.

Therefore, it is necessary to develop a method to check whether a collection of

objects and a membership relation defined on the collection satisfy the ZFC axiom

system.

Another interesting and important question, related to the concept of systems

modeling and systems identification, is: How can we bring in the idea of “noise”?

For instance, current achievements in modern quantum mechanics strongly support

the fact that the laws of nature, if any, are written in terms of probability. Also,

as pointed out by Masani (1994), each study of human relations is subject to the

correction of the human noise. In some sense, human noises are different from

those observed in any other systems containing no human beings.

356

Chapter 12

12.4. Laws of Conservation and the Multilevel Structure

of Nature

As shown in Section 12.1, the concept of systems characterizes the organi-

zational structure of the world, including the structure of layers. One inference,

based on the structure of layers, that can be made from the concept of systems is

that the world is finitely divisible. Hence, a system S

= (

, R

) is an n

th-level

object system of a system S

= (

, R

) if there exist systems S

= (Mi, Ri), for

i = 1, 2, … , n – 1, such that S

∈ M

–1

, for i = 1, 2, … , n, where n is a natural

number (Lin and Ma, 1987). Under the assumption that the ZFC axiom system is

consistent, the following has been shown: For any system S each chain of object

systems of

must be finite, where a sequence of systems, with

an ordinal

number, is a chain of object systems of S if S

is an i

th-level object system of

S, and for any i,

∈

, if i < j, there then is a natural number n(i,

) such that the

system

j is an n (i

)th-level object system of S

i . An object x is an nth-level ob-

ject of a system

(

, R

), where

is a positive integer, if there exist systems

= (

= 1,2,… ,

, such that S

∈ M

–1

, for i = 1, 2, … , n

, and

∈

If the object x is no longer a system, then it is called a fundamental object of S

The previous result then says that each system must be finitely divisible.

Based on this discussion, it can be shown that for any system S = (M, R

)

there exists a unique set M(S) consisting of all fundamental objects in S. The set

(

) is constructed as follows: For each object x ∈ M(

), there exists a chain

of object systems

for some natural number

(

), such that S

∈ M,

∈

–1

∈

, and x ∈ M

. Intuitively speaking, this result says that each system

is built on fundamental objects. Does this result imply that the world is made up

of fundamental particles, where a fundamental particle is a particle which cannot

be divided into smaller particles? We know that the world consists of atoms. A

fixed atom A can be thought of as a system S consisting of the set of all electrons

and the nucleus in A and a set of some relations between the electrons and the

nucleus. The collection of all electrons and the nucleus in A is a set because of the

finiteness of the collection. Generally, if a particle X can be divided into smaller

particles, it can be considered as an ordered pair (

M, R), where M is the totality of

the smaller particles in X, and R is a set of some relations between the particles in

M. Therefore, if M is a set, X can be described as a system. Hence, the previous

result implies that if M is a set, then X consists of fundamental particles. The last

conclusion is subject to three possibilities:

(i)

The world is made up of fundamental particles.

(ii)

There exists a particle X such that X can be divided into smaller particles

and the collection of all smaller particles in X is not a set.

(iii)

The ZFC axiom system is not consistent.

Some Unsolved Problems in General Systems Theory

357

Man has spent hundreds of years on the first possibility. When molecules were

first found, they were thought to be the fundamental bricks of the natural world.

Before long, smaller structures were found (i.e., atoms). At this time, people

really believed that the smallest bricks of the world were found. But, once again,

scientific achievement disproved that. Hence, people gradually began to believe

that there did not exist any fundamental particles in the world at all. Here it is

shown that each system is made up of fundamental objects. Can we conclude

that the world is made up of fundamental particles? This depends on whether the

second or third possibilities and the following reason are true:

There are some covert mistakes in the application of the result of systems

theory.

Because all classical mathematics, which has been the “unreasonably” effective

part of mathematics when applied to analyze practical problems, and consequently,

all modern science and technology can be developed on ZFC (Kunen, 1980), we

can be convinced that the ZFC axiom system is consistent. (Notice that there is no

way to prove this yet!): Now the reasons are: (1) There are some mistakes in the

application of systems theory. (2) There is a particle X such that X can be divided

into smaller particles and the collection of all smaller particles in X is not a set.

On the other hand, if the foregoing discussion is correct and if the world is

made up of fundamental particles, then each fundamental particle must be so small

that it has no size. Otherwise, it can still be cut into smaller pieces. Thus, under

the assumption that the world consists of fundamental particles, what the meaning

of particles is becomes an important problem, because each fundamental particle

cannot have a size.

As introduced by Klir (1985), a system is what is distinguished as a system.

We can do the following systems modeling: For each chosen matter, real situation

problem, or environment, such as a chemical reaction process, a system describing

the matter of interest can always be defined. For example, let S = (M, R ) be a

systems representation of a chemical reaction process, such that M stands for the

set of all substances used in the reaction and R is the set of all relations between

substances in

. It can be seen that S represents the chemical reaction of interest.

Changes of the system represents changes of the objects in M and changes of

relations in R. Based on this understanding and the result of systems theory that

each chain of object systems of a given system must be finite, the following axiom,

due to Lavoisier given in 1789, has been proven theoretically: In all the operations

of art and nature, nothing is created! An equal quantity of matter exists both

before and after the experiment … and nothing takes place beyond changes and

modifications in the combination of the elements. Upon this principle, the whole

art of performing chemical experiments depends.

Based on this understanding, the conservation principle of ancient atomists,

(Perlman, 1970, p. 414), which states that the total count of atoms in the universe

is constant, so the total amount of matter remains the same regardless of changes,

can be recast as follows:

358

Chapter 12

12.4.1.

Law of Conservation of Fundamental Particles

(Lin,

submitted)

The total count of fundamental particles in the universe is constant; therefore,

the total amount of matter remains the same regardless of changes and modifica-

tions.

Let us discuss some impacts of what has been done on the Law of Conservation

of Matter–Energy. The law states that the total amount of matter and energy is

always the same. Historically, this law was developed based on the new devel-

opment of science and technology: energy and matter are two different forms of

the same thing. That is, matter can be transferred into energy, and energy into

matter. All matter consists of fundamental particles, as already discussed and so

does energy. Since energy can be in different forms, such as light, it confirms

that each fundamental particle has no volume or size. Now, as a consequence of

the Law of Conservation of Fundamental Particles, the Law of Conservation of

Matter–Energy becomes clear and obvious.

One of the many important open problems is to develop conservation equations

in terms of fundamental particles and to write them in modern symbolic form. Only

with the indispensable “=” in the equations can the theory, developed on the Law

of Conservation of Fundamental Particles, become an “exact science” with the

capacity of prediction.

12.5. Set-Theoretic General Systems Theory

This section focuses on general systems theory developed on ZFC set theory.

As mentioned in Section 12.2, this general theory will establish a theoretical

foundation for all approaches of systems analysis developed in various disciplines.

Let

be a (general) system if

equals an ordered pair (

M , R ) of sets such that

R is a set of some relations defined on the set M (Lin, 1987). The elements in

M are called the objects of S and M and R are the object set and the relation set

of S, respectively. As pointed out by Mesarovic and Takahara (1989), an object

in M is recognized as a building block, a component of the system; it can be

real matter or a conceptual entity. Since the existence of an object is recognized

through its attributes or characteristics, a more appropriate definition for general

systems should be an ordered pair of a set of attributes of some objects and a set

of relations among the attributes of the objects. However, if one just simply uses

the attributes here as the objects, then the definition of general systems would be

reasonable.

For a relation r

∈ R, where S = (M, R) is a system, there exists an ordinal

number n = n(

) such that r ⊆ M

. The number n is called the length of r. It is

assumed that the length of the empty relation

is zero; that is,

= 0.

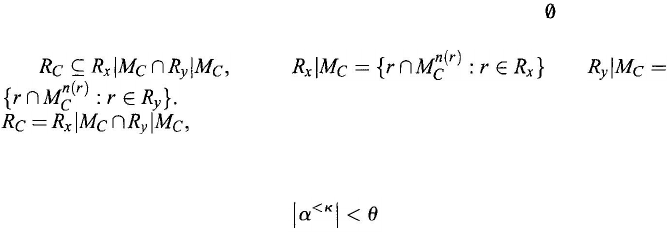
Some Unsolved Problems in General Systems Theory

359

One goal of systems theory, based on this definition, is to possess the same

beauty as mathematics possesses. Beauty ensures that the theory will be handed

down from generation to generation, since only beauty can make the theory as-

similated into our daily thoughts process and brought again and again before the

mind with ever-renewed encouragement. To achieve this goal, the general struc-

ture of a system, mappings from systems into systems, constructions of systems,

hierarchies of systems, etc., need to be studied systematically. Along this line are

several open problems.

It can be shown that for any system S = (M,R), where for any r

∈ R, n

(

) = 2,

S is a subset of the set p ²(M

)

∪p(p(M

)

∪

(

)), where p

¹(

X) = p

(

X) is the

power set of X and p

i +1

) =

(

)) for each i = 1,2,3,…. Is it possible that a

structural representation for general systems can be given similar to the one given

earlier? The characteristic of this representation is that only ordinal numbers and

power set operations are involved.

A system S = (M

R) is called centralized system if each object in S is a

system and there exists a system C = (M

, R

) satisfying

≠

such that for

any distinct elements

,y ∈ M, say x = (

) and y = (M

), MC = M

∩M

and

where

and

The system C is called a center of S. If in, in addition,

S is called strongly centralized. For centralized systems, it

has been shown that under the assumption that ZFC axiom system is consistent, for

κ an infinite cardinality and θ > κ a regular cardinality such that, for any α < θ,

then for each system S = (M

R) where |

| ≥ θ and |M

| < κ, for each object

∈ M a system with m = (M

, R

), and where there exists an object contained

in at least

θ objects in M, there exists a partial system S' = (

) of S such

that S' forms a centralized system and |M'|

≥ θ. This result is a restatement of

the general

∆-lemma in set theory (Kunen, 1980). Since this result has found

several interesting applications in sociology and epidemiology (Lin, 1988a; Lin

and Vierthaler, 1998; Lin and Forrest, 1995), it is worth asking: the question below:

Under what conditions is the partial system S' a strongly centralized system?

It can be seen that the concept of systems is a higher-level abstraction of math-

ematical structures. For example, n-tuple relations, networks, abstract automatic

machines, algebraic systems, topological spaces, vector spaces, algebras, fuzzy

sets and fuzzy relations, manifolds, metric spaces, normed spaces, Frechet spaces,

Banach spaces, Banach algebras, normed rings, Hilbert spaces, semigroups, Riesz

spaces, semiordered spaces, and systems of axioms and formal languages are all

systems. From these examples it is natural to consider the problem: Find proper-

ties of networks, automatic machines, topological spaces, vector spaces, algebras,

fuzzy structures, systems of axioms, etc., such that in general systems theory they

have the same appearance.

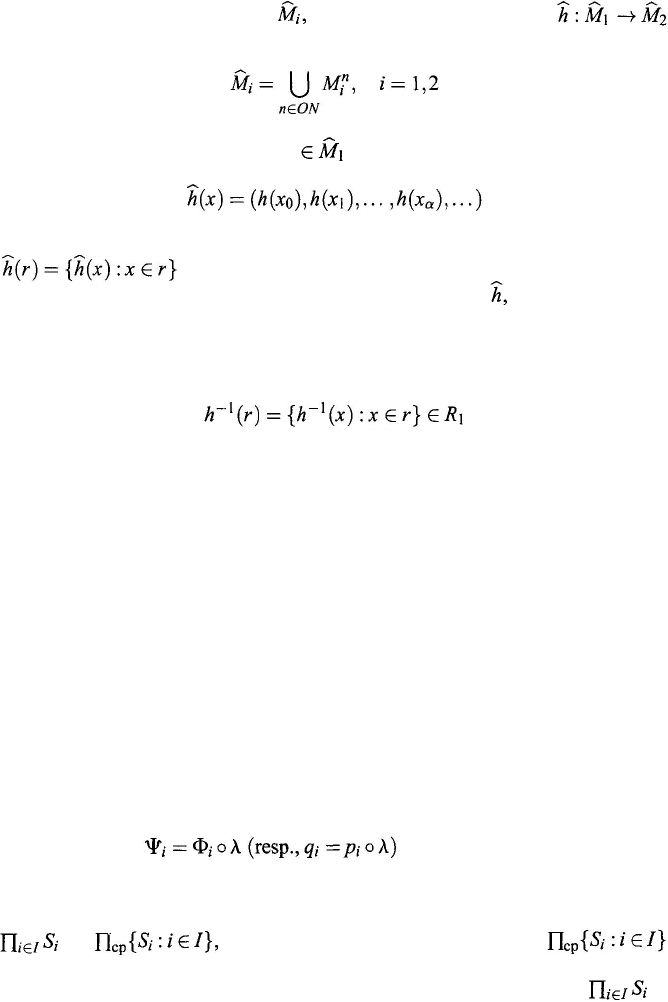
360

Chapter 12

Let S

= (M

), i = 1,2, be two systems and h : M

→ M

a mapping. By

transfinite induction, two classes i = 1,2, and a class mapping

can be defined with the following properties:

and for each x = (x

,…,x

,…)

where ON stands for the class of all ordinal numbers. For each relation r

∈ R,

is a relation on the set M

with length

(

). Without causing

confusion, h will also be used to indicate the class mapping

and

is a mapping

from

into

, denoted by

→

A mapping

= (

) → S

= (M

, R

) is S

-continuous (Ma and Lin,

1990e) if for any relation

∈

It then can be shown that if the systems S

, i = 1,2, are topological spaces, h is

-continuous iff

is a continuous mapping from the topological space

into the

topological space

, and that if the systems S

, i = 1,2, are rings in algebra, the

-continuity of h implies that h is a homomorphism from the ring S1 into the ring

. This example shows the need to find the topological properties of topological

spaces and algebraic properties of algebras, such as groups, rings, etc., such that

in systems analysis they have the same appearance.

A mapping ƒ : S

→ S

is a morphism from a system S

into a system S

if ƒ (R

) ⊆ R . Let Hom(S

, S

) = {ƒ : S

→ S

: ƒ is a morphism}. Suppose

{

: i ∈ I} is a set of systems. A system S = (M,R

) is a product (resp., Cartesian

product) of

, if there is a family of morphisms (resp., S

-continuous mappings)

{

∈

Hom(

) : i ∈ I

} (resp., {

: S → S

: i ∈ I

}) such that for each system

S' and a family {

∈

Hom(

) : i ∈ I) (resp., {

: S' → S

: i ∈ I} of S-

continuous mappings) there is a unique morphism (resp., S

-continuous mapping)

λ ∈ Hom(

) (resp., λ : S' → S) so that

for each i

∈ I

It can be shown that for each set {S

∈

} of systems, a product and a Cartesian

product of S

always exist, which are unique up to a similarity and denoted by

and respectively. The reason why the system

is called the Cartesian product of S

is that when S

are topological spaces, this

system is the Cartesian product of the spaces

. In this case, the system is

the box product of the spaces

. When the systems

are algebras, such as groups,

Some Unsolved Problems in General Systems Theory

361

rings, etc., the system ∏

∈I

is the direct sum of the algebras S

. That is, the box

product in topology and the direct sum in algebra have the same structure. This

fact gives rise to the following problem: Find topological structures and algebraic

structures such that in systems analysis they appear to be the same. Conversely, it

is natural to ask: When can a system be studied as a topological space or a specific

algebra?

Let (

≤ ) be a partially ordered set with order type α. An α-type hierarchy S

of systems [over the partially ordered set (T,

≤ )] is a function defined on T such

that for each t

∈ T, S(

) = S

(

) is a system (Lin, 1989a). For an α-type

hierarchy S of systems, let l

→ S

be a mapping from the system S

into the

system S

, for any r, t ∈ T with r ≥ t, such that

and

where r, s, t are arbitrary elements in T satisfying s

≥ r ≥ t and id

= id

is the

identity mapping on the set

. The family {

: t, s ∈ T,s ≥ t

} is termed a family

of linkage mappings of the α-type hierarchy S, and each l

is termed a linkage

mapping from the system S

into the system

It has been shown (Lin, 1989a) that for each

α-type hierarchy S of systems

satisfying that for each t

∈ T, M

≠

Ø where S

= (M

), there exists a family

{

: t,s ∈ T,s ≥ t} of linkage mappings of S. An interesting question is, how

many families of linkage mappings are there for a given

α-type hierarchy of

systems? Or, how many families of linkage mappings with certain properties,

such as S-continuous, are there for a given

-type hierarchy of systems? Another

question, which is similar to the question of expanding a given function, is the

following: Suppose S is an

-type hierarchy of systems over a partially ordered set

(

T, ≤) and {

ts : t,s ∈ T

, s ≥ t} is a family of linkage mappings of the hierarchy

of systems {

St : t ∈ T

}, where

⊂ T. Under what conditions does there exist a

family {

: t,s ∈ T, s ≥ t

} of linkage mappings for S such that

= l

for all s,

∈ T

with s ≥ t

As shown by Omran (197l), there is strong evidence for the existence of the

epidemiological transition, which describes the transition of health and disease

patterns, namely that infectious diseases are gradually replaced by noncommu-

nicable diseases as the economic and industrial development of a region takes

place. Its main characteristic is that the transition history of the health and disease

patterns of industrialized nations have been repeated, or are yet to be repeated,

in developing regions or nations. To model this important concept, Lin and Lin

(1995) employed the concepts of systems over groups and of periodic systems

over groups. To be specific, suppose (T, +,

≤ ) is an ordered Abelian group. A

hierarchy S of systems over (

≤

) is called a system over a group. If, in ad-

dition, the hierarchy is linked, the system is termed a linked system over a group.

For a fixed

∈ T, the right transformation of S, denoted S

–

, is defined to be

–

(

) = S

(

t – t

) for each t ∈ T; and the left transformation of S, denoted S

362

Chapter 12

and

is defined by S

(t) = S

(

t + t

) for each t ∈ T. A system S over a group T is

periodic if there exists p

∈ T such that p ≠ 0 and S

= S. The element p is called

a period of S. As pointed out in (Lin and Forrest, 1995), there is a need to study

multiperiodic systems where a system S over a group T is multiperiodic if there

exists a subset D

⊆ T such that S

= S for each p ∈ D.

Feedback has been a hot topic in recent years since all living, and many non-

living systems are feedback systems. How to study these systems is an important

question. The concepts of feedback transformation and feedback decoupling have

brought some light because they tell when the system under consideration can

be divided into smaller systems. For recent research, consult Takahara and Asahi

(1985), and Saito (1986; 1987). Let us take a brief look at the concepts of feedback

transformation and feedback decoupling and several related open questions.

Let

be a field, X and Y linear spaces over the field , and S an (input–

output) system satisfying the following conditions: (i) Ø

≠ S ⊆ X × Y ; (ii) s ∈ S

and s'

∈ S imply that s + s' ∈ S ; (iii) s ∈ S and α ∈

imply α · s ∈ S, where +

and · are addition and scalar multiplication in X

× Y, respectively, defined by: for

any (x

), (

) ∈ X × Y and any α ∈

(

) + (x

) = (

+ x

+ y

)

and

· (x

) = (α

). Then S is called an (input–output) linear system

(Mesarovic and Takahara, 1975). An input–output system

⊂

is a functional

system if S is a function from the input set X into the output set Y. Let S ⊂ X × Y

and S

: Y → X be a linear system and a linear functional system, respectively.

Then the feedback system of S by S

is defined as the input–output system S' such

that

The systems S and S

are called an original system and a feedback component

system, respectively. For details, see (Saito and Mesarovic, 1985).

Let = {S

⊂ X × Y : S is a linear system},

= {S

: Y → X : S

is a linear

functional system}; and = {S'

⊂ X × Y : S' is a subset}. Then a feedback

transformation

is defined by the last equivalence relation for each

The transformation F is called the feedback transformation over

the linear spaces X and Y.

Assume that the input space

and the output space

can be written

and For each

∈

the projection

= (

) : X × Y →

× Y

is defined by p

: X → X

and p

: Y → Y

satisfying p

(

x) = x

and

(

) = y

, for any x ∈ X and y ∈ Y. Let S

= p

(

S) for i ∈ I. Then the system S is

decomposed into a family of factor systems

is identified with

then

A linear

system S

∈ is decoupled by feedback (Saito and Mesarovic, 1985) if there is

ƒ ∈

such that

Some Unsolved Problems in General Systems Theory

363

Under the assumption that ZFC is consistent, it has been shown (Lin, 1994)

that if

∈

is decomposed into a family of factor systems

then S is

decoupled by feedback iff

and

where and

Based on this result, (Lin, 1994) gives a concrete procedure to decouple the linear

system

= Az + Bx

y = Cz + Dx

z(0) = 0

where z is an m

× 1 variable vector, called the state of the system, A, B, C, and D

are constant matrices of size m

× m, m × n, n × m, and n × n, respectively, such

that D is nonsingular, and the input space X and the output space Y are

X = Y = {

: [0,

∞

)

→

: r is piecewise continuous}

where is the set of all real numbers. The family of factor systems consists of n

one-dimensional linear systems of the following form:

= Az + B x

= C

z + D

z(0) = 0

for i = 1,2,

…

, n, where B = [

…

], C = [

…

]

, D

is a nonzero

constant, and the input space X

and the output space Y

are given by X

= Y

{

: [0,

∞

)

→

: r is piecewise continuous}.

Many questions are left open. For example, do the input space

and the output

space

have to be the same dimension in order to apply the theory? Find examples

of systems such that some of their important properties are not kept by feedback

systems. If some properties of the original system are not kept by feedback

systems, can the properties be studied by using the concept of pullback? For the

concept of pullback, see (Negoita, 1992). Is it possible to construct the solution

of the n-dimensional linear system described earlier, based on the solutions of the

one-dimensional factor systems?

12.6. Analytic Foundation for an Applicable General

Systems Theory

During a recent and fruitful conversation with Professor Pesi Masani, he

pointed out a fact, which could also be considered a challenge to systems sci-

ence, that to show the need for the concept of (general) systems it is absolutely

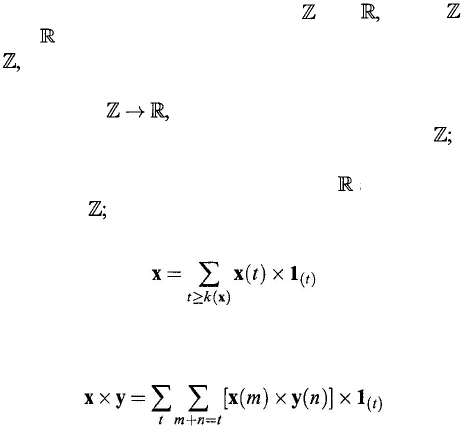
364

Chapter 12

necessary to obtain some results which have not or could not be achieved without

using the concept of systems. To meet this challenge and to make up a deficiency

of the current theory of general systems analysis, where no quantitative study

based on general systems analysis can be carried out, it will be shown that the non-

Archimedean number field, first introduced by Shu-tang Wang in the late 1970s

and early 1980s, is an excellent starting point.

Historically speaking, nonstandard analysis, established in the early 1960s by

Robinson (1977), introduced the concepts of infinitesimals and infinities formally

and legally, based on mathematical logic. This theory broke through the limitation

of classical concept of real numbers, where infinities are considered ideal objects.

With nonstandard analysis, many classical theories, such as mathematical analysis,

algebra, normed spaces, some classical mechanics problems, etc., can be greatly

simplified and become more intuitive. However, the shortfall of Robinson’s non-

standard analysis is that infinitesimals and infinities can only be shown to exist

and have no concrete expressions of any tangible form. Based on the argument

of the existence of infinitesimals and infinities given in Robinson’s theory, the

non-Archimedean number field, called the generalized number system (

GNS

) by

Wang (1985), has a computational advantage, since each number, whether ordi-

nary real number, infinitesimal, or infinity, has an exact expression in terms of the

real numbers in the classical sense.

A generalized number x is a function from

into

where

is the set of

all integers and the set of all real numbers, such that there exists a number

k = k

(

) ∈ called the level index of x, satisfying x

(

) = 0, for t < k, and

(

)) ≠ 0. Let GNS stand for the field consisting of all generalized numbers

and the zero function

with the following operations: (1) Addition and

subtraction: for any x, y

∈ GNS, (

)(

) = x

(

)

(

), for

∈

(2) Ordering:

for any x, y ∈ GNS, x < y iff there is a k

∈ I such that x

(

) = y

(

), if t < k

and x

(

) < y

(

); (3) Scalar multiplication: let c ∈ and x ∈ GNS, and define

(

x)(t

)

) for

∈

(4) Multiplication: for

∈

GNS,

write

as a generalized

power series

where 1

)

∈

GNS

is defined by

)

) = 0, if

≠

and

)

(

) = 1. Let

x, y

∈

GNS.

The product x × y or xy is defined by

(5) Division: For x, y

∈ GNS, if there exists a z ∈ GNS such that y × z = x, then

the generalized number z is called the quotient of x divided by y, denoted by x

÷ y

Throughout history, “laws” of nature have been frequently expressed and

treated with the rigor and beauty of mathematical symbols. For the most part,