Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.

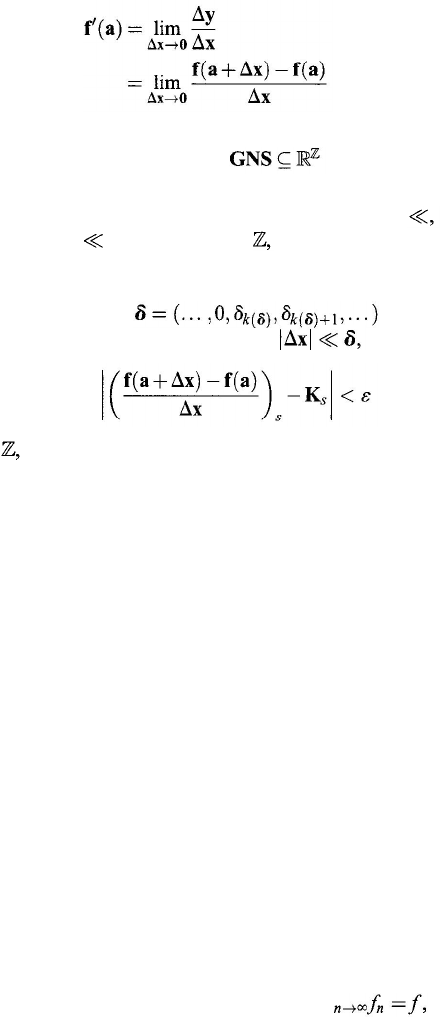
Calculus of Generalized Numbers
325
Then
f'
(a
)
is called the derivative of the function y = f(x
) at
a.
Symbolically,
(11.18)
Remark. Topologically speaking, the concept of derivative of f
(
x) at a ∈ GNS is
introduced so that the topological space
has the box product topology.
For more about this topology, see (Kuratowski and Mostowski, 1976).
For x, y ∈ GNS, a different ordering relation, denoted by on GNS can be
defined as follows: xy iff for each i
∈ x
i
< y
i
. With this ordering relation
on GNS, the weak derivative of y = f
(
x), a function from GNS into GNS, can be
introduced as follows (Wang, 1991): Suppose K
∈ GNS is fixed. If for each real
number
ε > 0, there exists with the property that
δ
j
> 0, for each j ≥ k
(
δ
), such that whenever
one has
for each
s
∈
then,
K
is called the weak derivative of
f
(
x
) at a, denoted f'
w
(
a
) = K.
11.4. Integral Calculus
11.4.1. Lebesgue Measures
For convenience and completeness of this chapter, we briefly look at some
elementary definitions and properties of Lebesgue integration, which is the center
of the theory of real analysis.
In classical mathematical analysis, functions which are continuous everywhere
are basically the center of the discussion of interest. However, as the theory
grew more mature and more applications were found, it seemed that it was no
longer sufficient to consider the everywhere continuous functions only. At first,
it was found that based on the consideration of continuous functions, the theory
established was often incomplete and also its applications were not flexible, at
the same time, it also seriously affected the development of the theory itself. For
example, the theory of integration of continuous functions was developed with the
theory of linear algebra as its background. This background has had great impact
on the establishment and development of the theory. However, even though it
was restricted to the study of continuous functions, under certain circumstances
the harmony between the two theories was destroyed. For example, the concept
of limits introduced in the space L
2
, denoted by lim
is different from
326
Chapter 11
This new concept of convergence has widespread applications. There are many
good reasons for introducing new concepts. For example, if it has been shown
that the boundary problems of partial differential equations of some problems in
physics do not have differentiable solutions, can one claim, based on this fact, that
these possess no practical meaning? Obviously not! since boundary problems are
often approximations of some realistic situations, they are idealized mathematical
models, and the coefficients of the differential equations in the models are not
absolutely accurate. Therefore, one should look at boundary problems from the
viewpoint of approximation. It is unreasonable to restrict ourselves to the range of
continuous and differentiable functions. Because of this, the concept of generalized
In the theory of Riemann integrals, to integrate each term of a given series,
the series must be uniformly convergent. Without uniform convergence, the limit
of a sequence of integrable functions may not be integrable at all, and therefore
there is no way for one to talk about integrating each terms and summing the
results. On the other hand, in applied situations, the requirement of uniform
convergence is often not satisfied or is so complicated that it only causes more
trouble. Similar problems exist in different areas of the old theory of integration.
Most arise because in the definition of definite integrals, too much emphasis is put
on the requirement of continuity. The essence of Riemann integrations involves
(1) cutting the interval into finitely many subintervals; (2) on each subinterval,
looking at the function value ƒ
(
x) as a constant; (3) improving accuracy of the
approximation by increasing the number of subintervals; (4) taking the limit to
achieve the desired accuracy. For this process to work,
ƒ
(
x
) cannot vary “too much”
on each of these subintervals. That is, ƒ
(
x) must be “fundamentally” continuous.
If
ƒ
(
x
) is “extremely discontinuous,” no matter how small each subinterval is, there
is no way that one can look at ƒ
(
x) as approximately a constant. The function is
If
ƒ
(
x ) is discontinuous, then we should try some new methods. For instance,
partition the interval into small subsets, on each of which ƒ(x) does not vary “too
much.” This is how the theory of Lebesgue integration was born.
The open interval A in the space is assumed to be the set of points
, where a
i
and
b
i
are constants. If A is an interval,
it means that some of the inequalities in its definition can contain the equals sign.
For any interval A,
⏐
A
⏐
stands for
, called the volume of A. Let E be
a set of points in , and
A
1
,
A
2
, . . . ,
A
n
, . . . a sequence of open intervals such that
. Then
is defined by
then considered to be not integrable.
the concept of lim
in mathematical analysis, where L² stands
for the space of all the functions which are Lebesgue square-integrable on
solutions was introduced.
. The exterior measure of E, denoted m
*
E,
’s are open intervals and
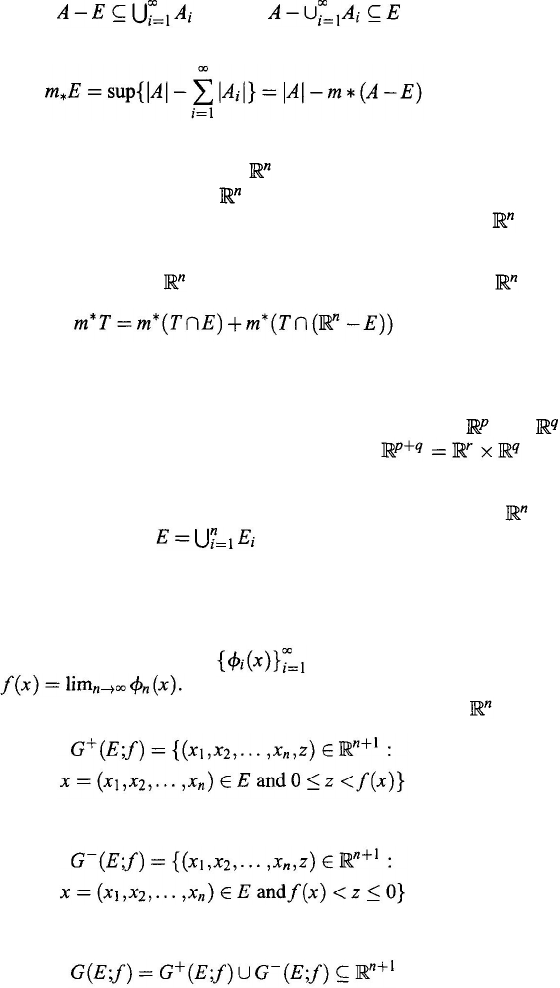
Calculus of Generalized Numbers
327
Let
A
be an interval such that
A
⊇
E
, and A
1
,
A
2
,... ,
A
n
, . . . a sequence of open
intervals such that . Hence, . Define the interior
measure of
E
, denoted as m
*
E, by
If
m
*
E = m
*
E
, the set
E
is Lebesgue measurable or simply measurable. Therefore,
the collection of all bounded subsets of is classified as measurable or not
measurable. An unbounded set B
⊆ is measurable if B ∩ A is measurable
for each chosen interval A. One equivalent condition for a subset A
⊆ to be
measurable is given in the next theorem.
Theorem 11.4.1. A subset A
⊆ is measurable iff, for any subset T ⊆ ,
In this case, the exterior measure of A is called the measure of A and is denoted
by mA.
Theorem 11.4.2. Assume that A and B are measurable subsets in and ,
respectively. Then C = A
× B is a measurable subset in , and
m
(
C) = mA × mB.
Let ƒ
(
x ) be a real-valued function defined on a measurable set E ⊆ . If
there is a partition of the subset
such that on each
E
i
the function
ƒ
(x
)
is a constant, ƒ
(
x) is a simple function. It is obvious that the sum and product
of simple functions are still simple functions. However, the limit of a sequence
of simple functions may not be a simple function at all, since a simple function
can only have a finite number of different function values. A function ƒ(x ) is
measurable on E if there is a sequence
of simple functions, defined on
E
, such that
Let
ƒ
(
x ) = ƒ
(
x
1
,
x
2
, . . . ,
x
n
) be a function defined on a subset E ⊆ . Define
and
The set
is called the graph of ƒ(x).
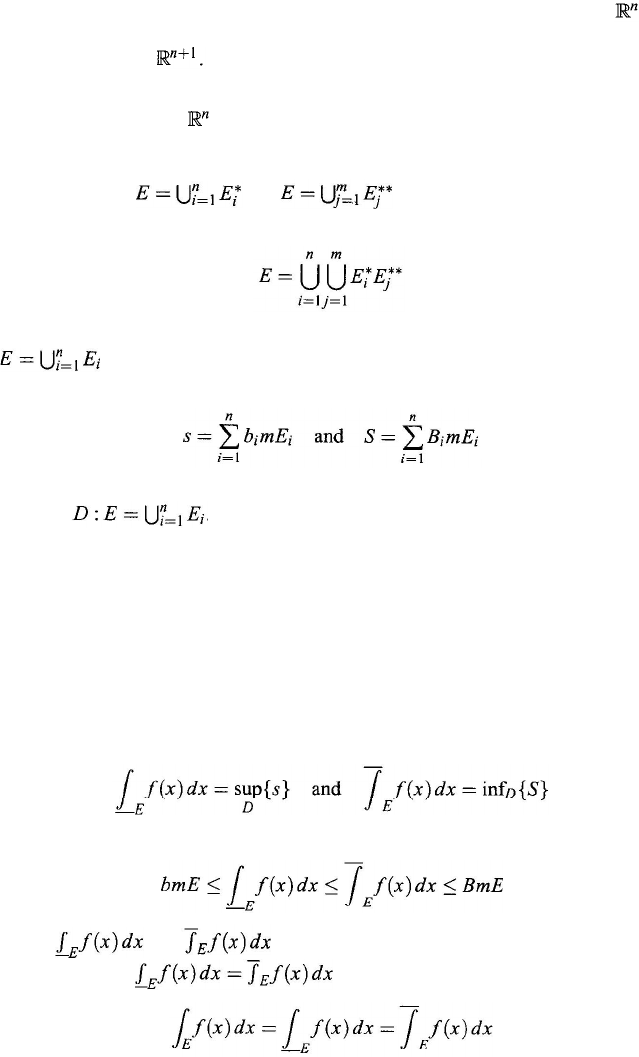
328
Chapter 11
Theorem 11.4.3. A function ƒ
(
x
) defined on a measurable subset E ⊆
is
measurable iff the graph G(
E
;
ƒ
) of the function is measurable in the (n + 1) -
dimensional space
Now it is time to look at the concept of Lebesgue integrals.
Case 1: Let E
⊆ be a measurable subset with mE < +
∞
, and ƒ
(
x) a
bounded function defined on E. Let us see how the Lebesgue integral of ƒ
(
x) is
defined.
Assume that
and are two partitions such that each
E
i
*
and E
j
**
are measurable. It is obvious that
is also a partition, which is a finer partition than either of the previous two. For
, let b
i
and
B
i
be the greatest lower bound and the least upper bound
of ƒ
(
x ) on E
i
; i.e., b
i
≤
ƒ
(
x) ≤ B
i
for each x ∈ E
i
. Define
which are called the small sum and the big sum of the function with respect to the
partition . Obviously, one has
bmE
≤ s ≤ S ≤ BmE
where b and B are the greatest lower and the least upper bounds of ƒ(
x) on E
,
respectively. It can be shown that if D
*
is a finer partition than
D
and if
s
*
and S
*
are the small sum and the big sum of ƒ(
x) with respect to D
*
, then
s
≤ s
*
≤ S
*
≤
S
No matter what kind of partition
D
is, the small sum and the big sum are always
between bmE and BmE one can thus define
Then
where
and
called the lower integral and the upper integral
of
ƒ
(
x) on E. If
, then
ƒ
(
x) is integrable and written as
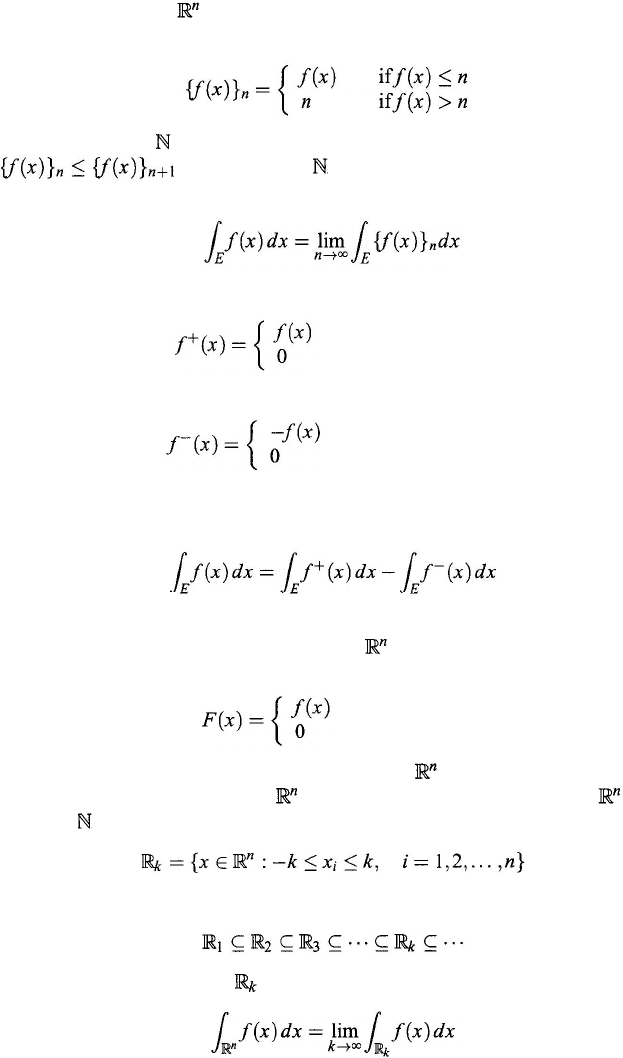
Calculus of Generalized Numbers
329
Case 2: Let E ⊆ be a measurable subset with mE < + ∞, and ƒ(x) ≥ 0 a
nonnegative function defined on E. To define the integral of ƒ(
x
) on
E
, let
for any fixed n
∈ . Then {
ƒ
(
x
)}
n
, is a bounded function on E and satisfies
. If for each n
∈ , {f
(
x
)}
n
is integrable on E, then ƒ
(
x) is
integrable on
E
, and we write
For a general function ƒ(
x
) defined on
E
, define
when ƒ
(
x) ≥ 0
when
ƒ
(
x) < 0
and
when
ƒ
(
x
)
≤ 0
when
ƒ
(
x) > 0
If f
+
(
x
) and f
–
(
x) have integral values on E which are not both infinities, then
ƒ
(
x) has integral value on E, which is denoted by
If the integral values of f
+
(
x) and f
–
(
x) are finite, ƒ
(
x) is integrable on E.
Case 3: Let E be a measurable subset of
and
ƒ
(
x) a function defined on E.
Define
if x ∈ E
otherwise
Then F
(
x
) is a function defined on the entire space
. Without loss of generality,
let ƒ
(
x) be a function defined on . First, assume ƒ(x) ≥ 0 for all x ∈ . For
each k
∈
, define
Then
If ƒ
(
x) is integrable on each
, define
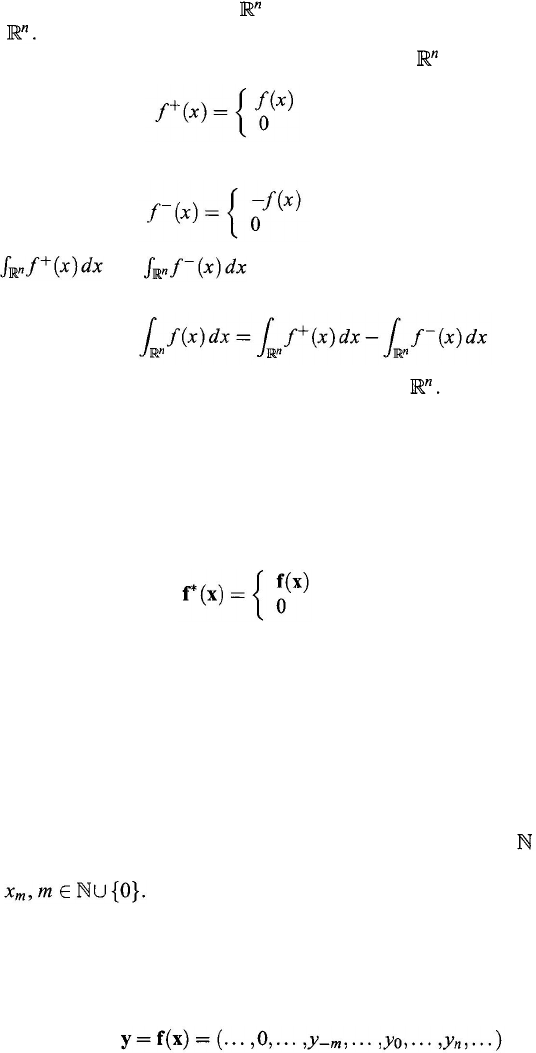
330
Chapter 11
as the integral value of ƒ(x) on . When this is value is finite, ƒ
(
x
) is integrable
on
Second, let
ƒ
(
x
) be a general function defined on
. Define
when ƒ
(
x) ≥ 0
when
ƒ
(
x ) < 0
and
when ƒ
(
x ) ≤ 0
when
ƒ
(
x) > 0
If
and
are meaningful, define the integral value of
ƒ
(x
)
as
If these two integrals are finite,
ƒ
(
x
) is integrable on
.
11.4.2. Integrals on GNS
Let us now turn our attention to the concept of integrals of functions defined
on
GNS
. Let f : E → F be a function from a subset E of GNS into a subset F of
GNS
. Define a new function f
*
:
GNS
→
GNS
as follows:
if
x
∈
E
otherwise
Without loss of generality, it can be assumed that each function f from a subset of
GNS
into a subset of
GNS
is a function from
GNS
into
GNS
.
To make this chapter self-contained, the definition of integrals of functions
defined on GNS, studied in Chapter 6 will be reintroduced. After that, new
concepts of definite integrals and indefinite integrals will be studied. We define
the integral, called a GNL-integral, with GNL standing for generalized number
and Lebesgue, of functions defined on GNS inductively as follows. For a given
function
f
:
GNS
→
GNS
, let E = {
x
∈
GNS
:
f
(
x
) ≠ 0
}.
Case 1: Suppose that for each x ∈ E, x
–m
= 0, for all m ∈ and that y =
f
(
x
) = (. . . , y
–m
, . . . ,
y
0
. . . , y
n
, . . .), where, in general,
y
k
= y
k
(
x
) is a function of
all
Step 1: Define a subset H
(0)
⊆
as follows: a
0
∈
H
(0)
iff
y
–m
= 0 if m > 0
and
y
0
=
y
0
(
a
0
)
a function of
a
0
(11.19)
where

Calculus of Generalized Numbers
331
whenever
x
= (. . . , 0,
a
0
, x
1
, x
2
, . . .), with
x
(
k
(
x
)) =
a
0
; let
(11.20)
If the real-valued function ƒ
(0)
is Lebesgue integrable on
then
– H
(0)
has
Lebesgue measure zero, and set
Step n:
Assume the real numbers
a
(0)
, a
(1)
, . . . ,a
(n–1)
have all been defined.
For any fixed
x
0
, . . . x
n –1
, define a subset H
(n )
⊆
as follows:
a
n
∈ H
(n )
iff
and a function of
a
n
where
whenever
let
(11.21)
(11.22)
If the real-valued function
is Lebesgue integrable on , denote the
integral on
by
a
(n )
(
x
0
, . . . ,
x
n
– 1
). If
is meaningful,
that is — if there are only countably many nonzero summands and the summation
is absolutely convergent, then the sum is denoted by
a
(n )
.
Definition 11.4.1 [Wang (1985)]. If
is convergent and equals a, then
the function f
(
x
) is GNL-integrable, written
Case 2: Partition the set E = {x
∈ GNS : f
(
x
) ≠ 0} as follows:
where
E
k
= {x ∈ E : k
(
x
) = –k}. For each fixed k ∈ , consider
the right-shifting of and the left-shifting of
f
(
x
):
First, define a new function
f
(0)
: GNS → GNS by
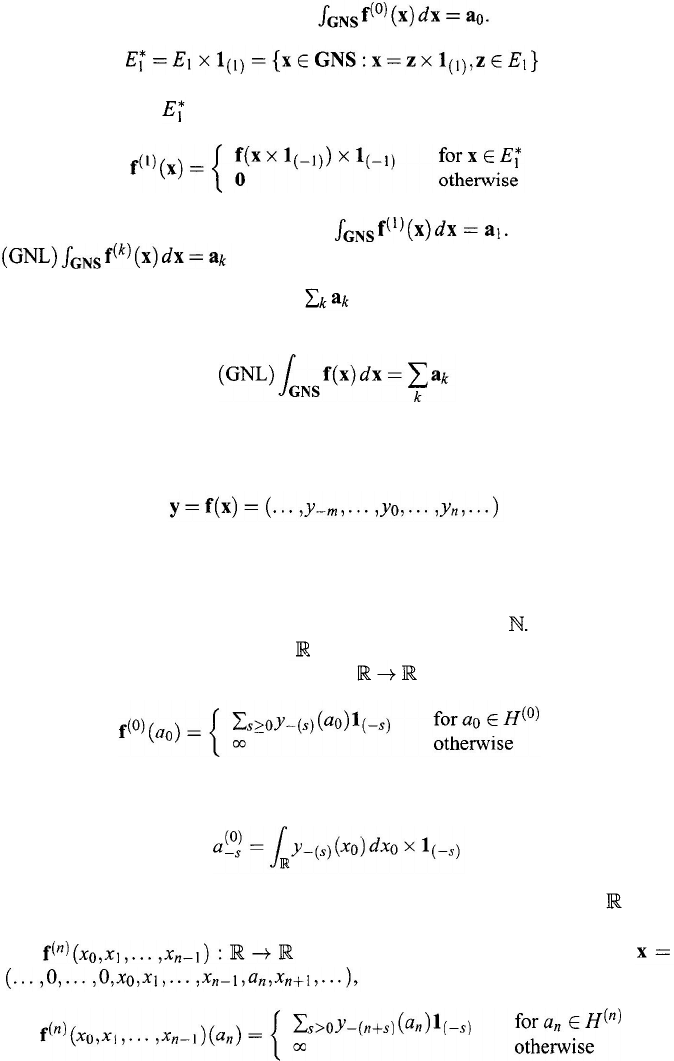
332
Chapter 11
If f
(0)
is GNL-integrable, write (GNS) Second, define
That is, for any
x
∈
, k
(
x
) = 0. Define a new function
f
(1)
: GNS → GNS by
If f
(1)
is GNL-integrable, write (GNL)
In general, write
if f
(k )
is GNL-integrable.
Definition 11.4.2
[Wang (1985)].
If
is convergent, then the function
f
(
x
) is
GNL-integrable and written
A concept called (G) integrals was introduced by Wang (1985). Let
f
:
GNS
→
GNS be a function and E = {x ∈ GNS : f
(
x
) ≠ 0
}. Let
As before, the concept of (G) integrals will be introduced in two parts. The first
part is a special case, while the second part generalizes the first.
Case 1: Suppose that for any x
∈ E the generalized number x takes the form
x
= (… , 0,
x
0
,
x
1
, . . . ,
x
n
, . . . ). That is,
x
–m
= 0, for each
m
∈
Step 0:
Define a subset
H
(0)
⊆
such that
a
0
∈ H
(0)
iff y
–m
= y
–m
(
a
0
) is a
function of
a
0
only for all m ≥ 0. Let f
(0)
:
be a function defined by
If each
y
–(s
)
(
a
0
) is Lebesgue integrable,
s
= 0, 1, 2, . . . , write
Step n: Let x
0
, x
1
, . . . , x
n –1
be fixed. Define a subset H
(n)
⊆
such
that a
n
∈ H
(n
)
, iff y
–m
= y
–m
(
a
0
) is a function of a
0
only for all m ≥ n.
Let
be a function defined as follows:
if
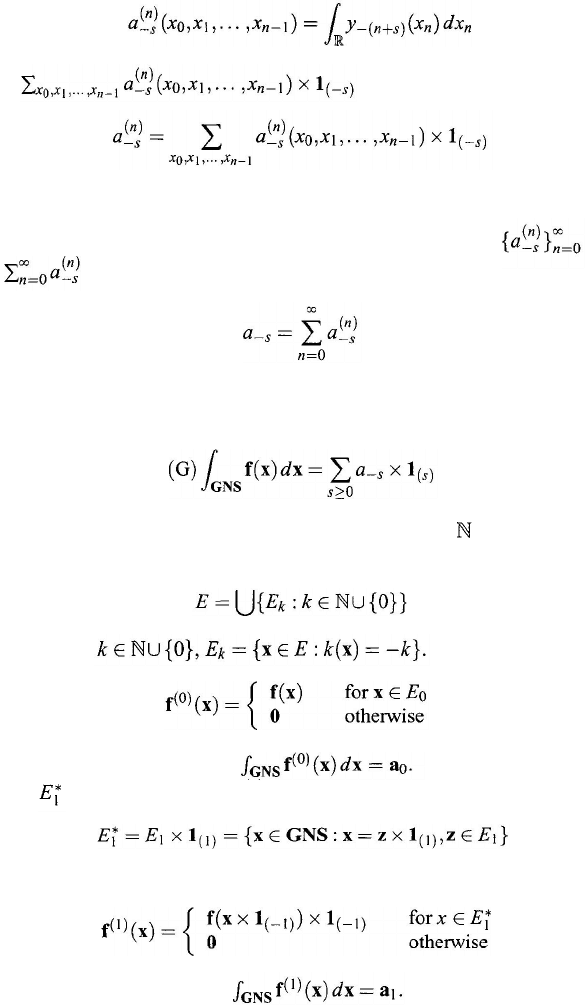
Calculus of Generalized Numbers
333
If each
y
–(n+ s )
(
a
n
) is Lebesgue integrable,
s
= 0, 1, 2, . . . , write
and if
exists, denote it by
for
s
= 0, 1, 2, . . . .
Definition 11.4.3 [Wang (1985)].
For each
s
≥
0, if the sequence exists
and
is convergent, define
If there are only a finite number of natural numbers s such that a
– s
≠ 0, then the
function ƒ
(
x) is (G)-integrable, denoted
Case 2: Suppose that for some x
∈ E there exists m ∈
such that x
–
m
≠ 0.
Partition the set E =
{
x ∈ GNS : f
(
x
) ≠ 0
} as
where for each
First, define
If f
(0)
is (G)-integrable, let (G)
Second, define the right-
shifting
of
E
1
and a function
f
(1)
:
GNS
→
GNS
by
and
If f
(1)
is (G)-integrable, set (G)
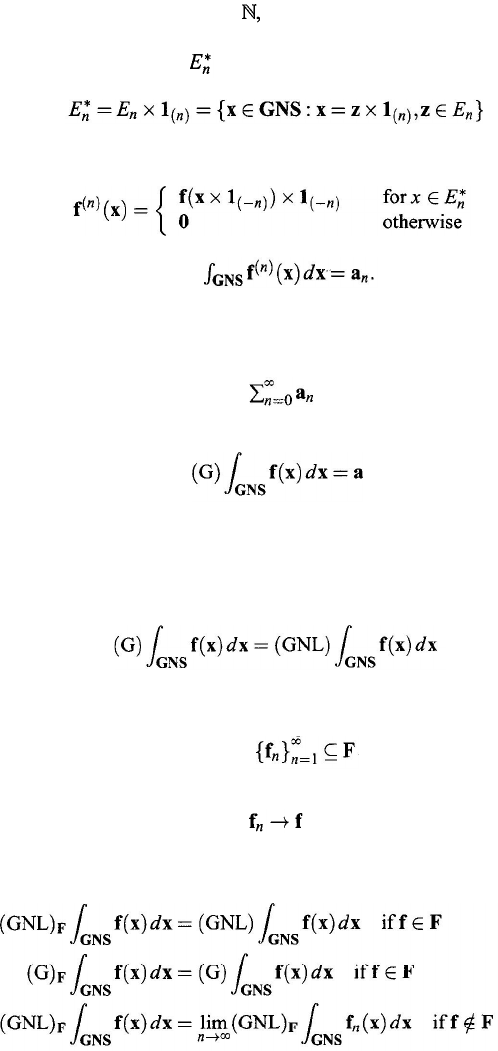
334
Chapter 11
and
Inductively, assume that for n ∈
the generalized numbers
a
0
,
a
1
,
a
2
, . . . ,
a
n
have been defined. Now a generalized number a
n +1
can be defined as follows:
First, define the right-shifting of
E
n
and a function
f
(n )
: GNS → GNS by
If f
(n )
is (G)-integrable, let (G)
By mathematical induction it follows that if all the generalized numbers
a
0
,
a
1
,
a
2
, . . . , a
n
, . . . have been defined as before, then we can make the following
definition.
Definition 11.4.4 [Wang (1985)].
If
is convergent to a generalized num-
ber a, then the function f is (G)-integrable,
The following result is clear.
Theorem 11.4.4.
If
f : GNS → GNS is (GNL)-
integrable, it is then
(G)-
integrable
and
(11.23)
Now let F be a family of (GNL)-integrable (resp., (G)-integrable) functions.
Suppose that a convergence relation among functions defined on GNS has been
chosen such that there exist a sequence
and a function
f
:
GNS
→
GNS
such that
(11.24)
The (
GNS
)
F
-integral (resp., (G)
F
-integral) of f is defined as follows:
(11.25)
(11.26)
(11.27)
