Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.

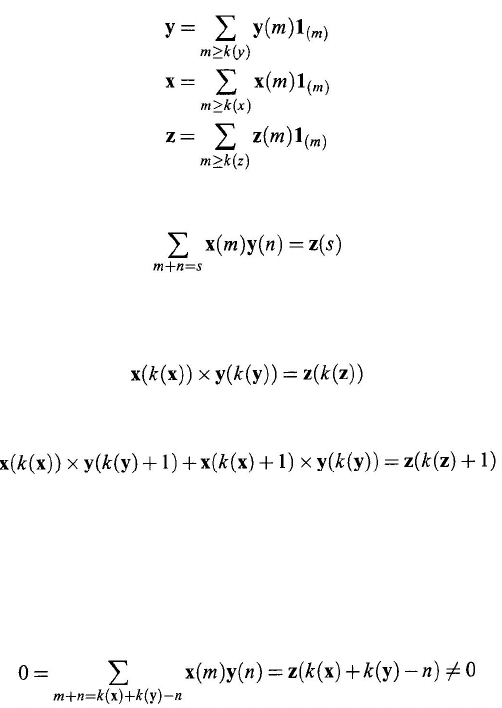
Calculus of Generalized Numbers
The proof is straightforward and omitted.
Theorem 11.1.3. Let x, y
∈ GNS such that y ≠ 0 ≠ x. Then
(1)
k(
x
+
y
) ≥ min{ k(x
),
k
(y
)}.
(2)
k(x × y) = k(x) + k (y).
(3)
k(x/ y) = k (x) – k (y).
315
Proof: The argument for (1) is straightforward and is left to the reader.
The proof of (2). Assume that z = x
× y and that
Hence, x
× y = z is equivalent to, for any integer s,
(11.9)
where k (x) ≤ m ≤ s –
k(y) and k(y)
≤ n ≤ s – k (
z
). We can now define k(z) =
k(x) + k(
y
). When s
= k (z), Eq. (11.9) becomes
When s = k
(
z) + 1, Eq. (11.9) becomes
By applying induction on the index
k
(z
) +
i,
the generalized number
z
can be well
defined.
To show the uniqueness of the index number k(z), it suffices to see that
k(z) cannot be less than k
(
x
) + k
(
y), as defined. To this end, assume k
(
z
) =
k(x
) +
k
(y
) –
n,
for some nonzero whole number
n.
Replacing
s
by
k
(x) + k(y) – n
in Eq. (11.9) gives
contradiction. That is, the definition of k(z) is unique. This ends the proof of (2).
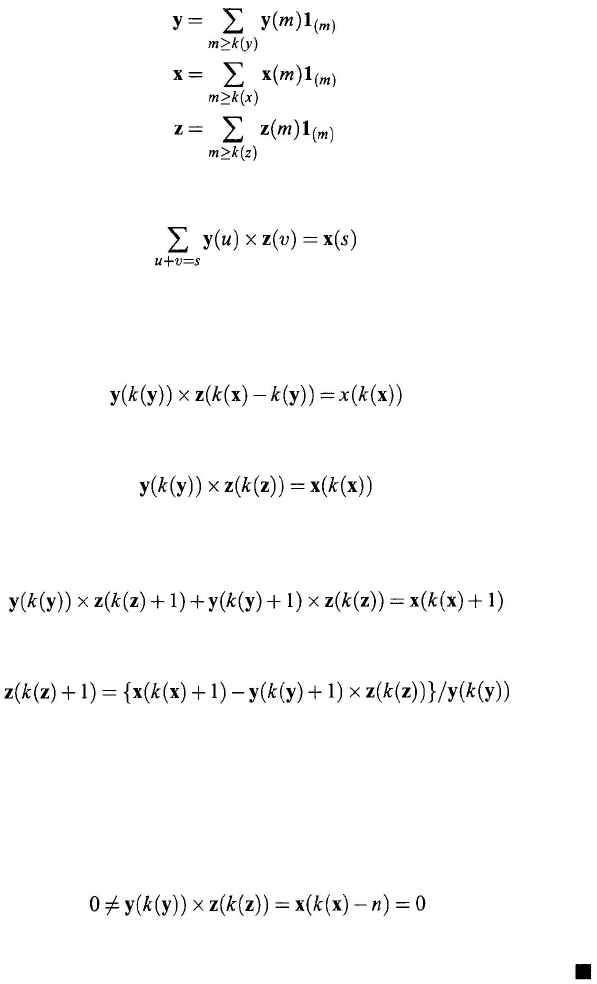
316
Chapter 11
Proof of (3). Let z = x
/
y
. Assume that
Then these numbers satisfy
(11.10)
with k
(
y
) ≤ u ≤ s – k(
z
) and k(
z
) ≤ v ≤ s – k (
y
). This second inequality implies
that we can define k(
z
) = k(
x
) – k(
y
). Hence, replacing s by k(
x
) in Eq. (11. 10),
one has
That is,
Thus, z(k(
z
)) = x(k(
x
))/
y
(k(
y
)). When s is replaced by k(
x
) + 1 in Eq. (11. 10),
one has
Therefore,
By induction, we can continue this process and define each z(
m
) for m ≥ k(
z
) =
k(
x
) – k(
y
). Thus, the relation between the generalized numbers z, x, and y can
be found.
The uniqueness of k(
z
) can be shown as follows: Assume that k(
z
) = k
(
x
) –
k(
y
) – n for some nonzero whole number n. Then replacing s by k(
x
) – n
in
Eq. (11.10) gives
contradiction. The whole number n must therefore be zero. That is, k(
z
) must be
unique.
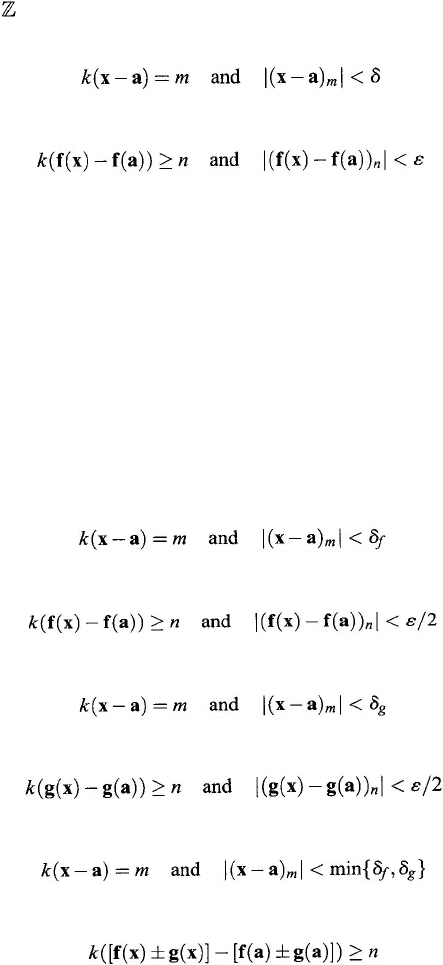
Calculus of Generalized Numbers
317
11.2. Continuity
Let E be a subset of GNS and f : E → GNS a function. For a fixed a ∈ E and
fixed m
,
n
∈
, if for any real number ε > 0 there exists a real number δ > 0 such
that, for any x
∈ E
imply that
then f(
x
) is quasi-(
m
, n) continuous at point a (Wang, 1985). A special case of
quasi-(
m
, n) continuity is quasi-(0, 0) continuity, which is the ordinary definition
of continuity of real-valued functions.
If n < m , Theorem 11.1.2 implies that
when the function value is infinity, one can still study the concept of continuity.
That is, the concept of continuity is expanded to include the study of continuity of
infinities.
Theorem 11.2.1. If f(
x
) and g(
x
) are quasi-
(
m
, n) continuous at a point a, then
so are the functions h(
x
) = f(
x
) + g(
x
) and k(
x
) = f(
x
) – g(
x
).
Proof: Since f(
x
) and g(
x
) are quasi-(m, n) continuous at point a, by the
definition of quasi-(
m, n) continuity, for any real number ε > 0, there exist real
numbers
δ
f
> 0
and δ
g
> 0 such that for any
x
∈
GNS
,
imply that
and that for any
x
∈
GNS
,
imply that
Therefore, for any
x
∈
GNS
satisfying
one has

318
Chapter 11
and
That is, it has been shown that h(
x
) and k(
x
) are quasi-(
m
, n) continuous at the
point
a
.
Theorem 11.2.2. Assume that the functions f(
x
) and g(
x
) are quasi-(
m
, n
1
) and
(m, n
2
) continuous at a point a, respectively. Then the product function h(
x
) =
f
(
x
)
g
(
x
) is quasi-(
m
, n) continuous at point a, where n = min{k(
f
(
a
)) + n
2
, n
1
+
k(g(
a
))}.
Proof: Since f(
x
) and g(
x
) are quasi-(
m
, n
1
) and quasi-(
m
, n
2
) continuous at
a, respectively, from the definition of quasi-(
m
, n) continuity, it follows that for
any real number
ε > 0 there exist real numbers δ
f
> 0 and δ
g
> 0 such that, for
any
x
∈
GNS
,
imply that
and
k(
f
(
x
)) = k(
f
(a)) ≤
n
2
, and for some real number
M
; and that
for any
x
∈
GNS
,
imply that
and
Therefore, for any
x
∈
GNS
satisfying

Calculus of Generalized Numbers
319
one has
and
It has thus been shown that h(
x
) = f(
x
)
g
(
x
) is quasi-(
m
, n) continuous at a.
Theorem 11.2.3. Assume that f(
x
) is quasi-(
m
, n
f
) continuous at a point a and
that g(
x
) is quasi-(
m
, k (
g
(
a
)))
continuous at a such that g(
a
) ≠ 0 . Then, the
quotient function
f
(
x
)/
g
(
x
) is quasi-(
m
, n) continuous at a, where n = min{n
f
–
k(
g
(
a
)), k(
f
(
a
)) – k (
g
(
a
))}.
Proof: From the assumption that g(
x
) is quasi-(
m
, k(
g
(
a
))) continuous at a, it
follows that for any real number
ε
> 0 there exists a real number
δ
g
> 0 such that,
for any
x
∈
GNS
,
imply that
and k(
g
(
x
)) = k(
g
(
a
)), where
for some fixed positive
numbers m, M ∈
The quasi-(
m
,
k
(
g
(
a
)))
continuity of
g
(
x
) at a guarantees the
existence of m and M.

320
Chapter 11
Now from the assumption that
f
(
x
) is quasi-(m, n
f
) continuous at a, it follows
that for any real number
ε > 0, there exists a real number δ
f
> 0 such that for any
x
∈
GNS
,
imply that
and
Now let x ∈
satisfy
Then from Theorem 11.1.3 it follows that
and that
Therefore, the quotient function is quasi-(
m, n) continuous at a.

Calculus of Generalized Numbers 321
11.3. Differential Calculus
In order to simplify the discussion, let us look at the concept of 〈ε
–
δ〉 limits
in GNS first. Assume that f : GNS
→ GNS is a function and a ∈ GNS a fixed
generalized number. For a fixed L
∈
(11.11)
stands for the fact that for fixed integers m and n, for any real number
ε > 0 there
exists a real number
δ > 0 such that for any x ∈ GNS,
imply that
In this case, Eq. (11.11) is read as the quasi-(
m, n
) limit of f
(
x
) at a is L.
Let S
∈ be fixed such that for fixed m, n ∈
for each real number ε > 0
there exists a real number
δ > 0 such that, for any x ∈ GNS,
(11.12)
imply that
(11.13)
and
(11.14)
Then the generalized number S × 1
(
n–m
)
is called the (m,n )-derivative of the
function f at a (Wang, 1985). In this case, f is (m,n)-differentiable at a, and the
(m,n )-derivative will be written as
(11.15)
It is obvious that the (0, 0)-derivative of f is the ordinary derivative of real-valued
functions.
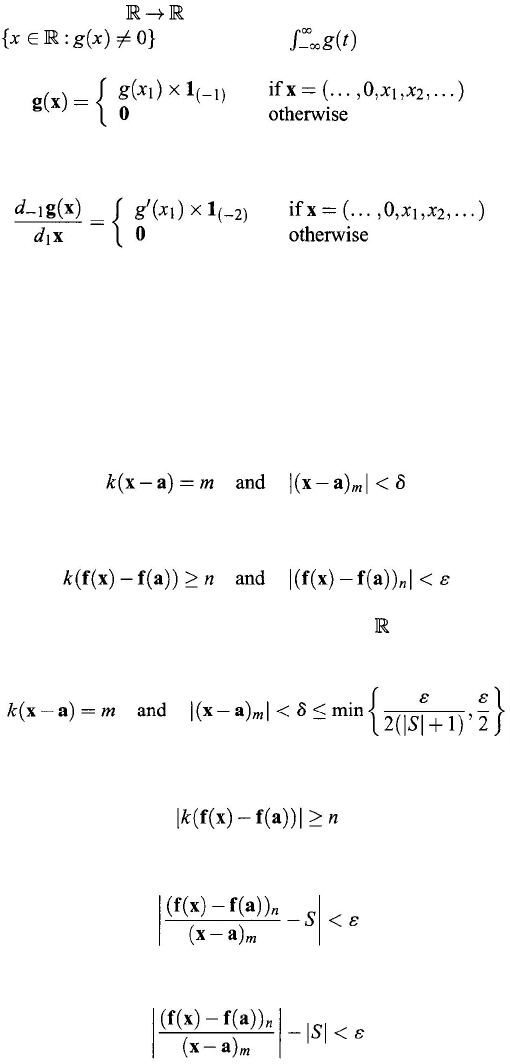
322
Chapter 11
Example 11.3.1.
Let
g
: be an infinitely differentiable real-valued function
such that is bounded and dt = 1. Define
It can be shown that the (1,–1)-derivative of g : GNS
→ GNS is
Theorem 11.3.1. If a function f : GNS
→ GNS is (
m,n
)-differentiable at a point
a
∈ GNS, then f is quasi-
(
m,n
)
continuous at
a
.
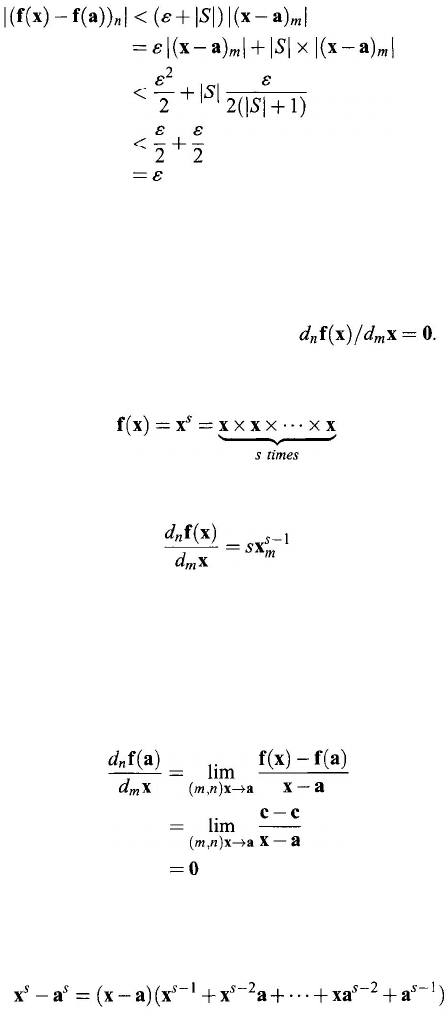
Proof: To show that f is quasi-(
m,n
) continuous at
a
, let ε be an arbitrary real
number such that 0 <
ε < 1. It suffices to show that there exists a real number
δ > 0 such that, for any x ∈ GNS,
imply that
Since f is (m,n
)-differentiable at
a
, there exists an S ∈ such that for the chosen
ε > 0, there exists a real number δ > 0 such that, for any x ∈ GNS,
imply that
and
So
Calculus of Generalized Numbers 323
and
That is, f is quasi-(m,n ) continuous at a.
Theorem 11.3.2.
(1) If
f
(
x
) = c ∈ GNS is a constant function, then
(2) If s is a positive integer and
then
where m = k
(
x) and n = sm.
Proof:
(1) From Eq. (11.15), it follows that for any fixed a ∈ GNS,
(2)
For any
x, a
∈
GNS,
the axioms of a non-Archimedean ordered field (see
the proof of Theorem 11.1.1) can be used to prove that
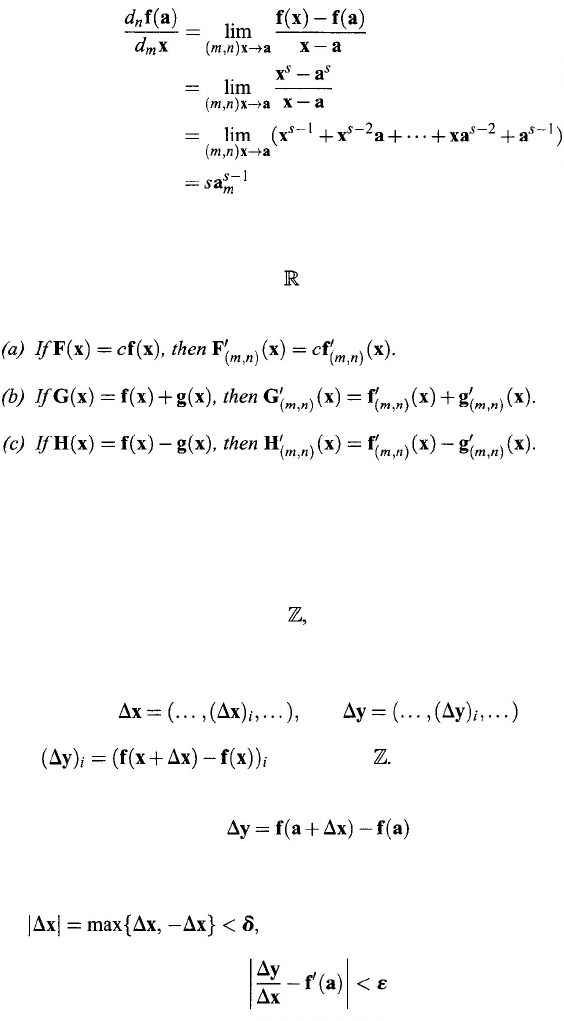
324
Chapter 11
Therefore, for m = k
(
a
) and n = sm,
Theorem 11.3.3. Suppose that c ∈ is a constant and f'
(
m,n
)
(x
)
and g'
(m,n
)
(
x
)
exist. Then
The proof is straightforward and is omitted.
One problem with the concept of (
m,n
)-derivative is that the derivative is a
generalized number in I
(
n–m
)
. In (Wang, 1991), this problem was corrected by the
following methods.
Suppose y = f (x
) = (. . . ,
y
–m
, . . .
,y
0
, . . .
,y
n
, . . .)
is a function from
GNS
into
GNS.
Then, for each fixed index
k
∈
y
k
is a function of x. That is, in general y
k
depends on an infinite number of variables
x
0
,
x
1
,x
–1
,
x
2
,
x
–2
, . . .
As in the calculus
of real-valued functions, let
∆
x and ∆y represent increments of x and y such that
where
for each i ∈
Let a ∈ GNS be fixed. Let
(11.16)
If there exists a generalized number, denoted f'(a), such that for each generalized
number
ε
>
0,
there exists a generalized number
δ
>
0
satisfying, for all
∆
x ∈ GNS
with
(11.17)
