Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

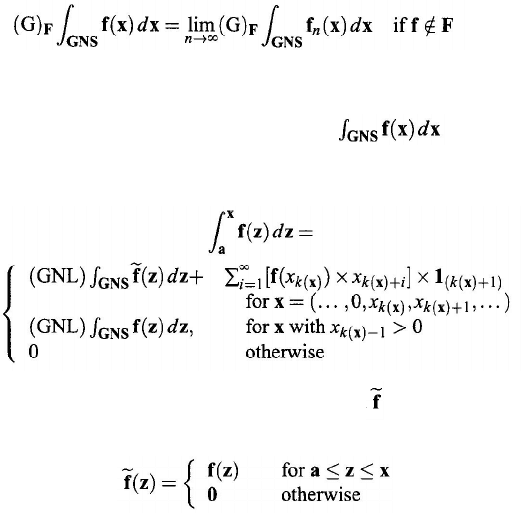
Calculus of Generalized Numbers

335

and

(11.28)

where it is assumed that the limits exist.

The concept of indefinite integral of a function f : GNS

→ GNS was studied

by Wang (1985) as follows. Assume that (GNL) exists and that the

function value of

(

) depends only on the real variable x

k (x)

. Then the indefinite

integral of y =

(

) is defined as

where

= (… ,

–m

, … ,

, …) is fixed, and : GNS → GNS is defined

11.5. Schwartz Distribution and GNS

11.5.1. A Nontechnical Introduction to Schwartz Distribution

The theory of distributions was developed to correspond to situations presented

to the world of learning by physical experiences which are not adequately covered

by the classical y = ƒ

(

x) notion of a function in mathematical analysis. Here,

the word “physical” really means “phenomenological” — i.e., pertaining to the

phenomena of nature. The concept of distributions, as introduced and codified by

Laurent Schwartz (1950; 1951), has been widely used to tie many important and

different instances, occurring in different parts of the world of learning, together.

A “distribution” is a kind of “generalized function.” The class of all distribu-

tions or generalized functions includes many objects which are not functions at

all in the sense of classical mathematical analysis. The reason why it is necessary

to study the theory of distributions is not mere generality; rather, the theory has a

coherence and a power that the theory of mathematical analysis lacks. There are

many aspects of this conceptual power. For example, the operation of taking a

derivative applies without restriction to distributions. That is, the derivative of a

336

Chapter 11

Figure 11.1. A pulse function supported on [0,1].

distribution always exists and is another distribution. Since continuous functions

are distributions, the operation of taking a derivative in the theory of distributions

eliminates the defect of mathematical analysis, where many continuous functions

have no derivatives.

A function is a test function if

(a)

is infinitely differentiable.

(b)

φ has compact support; i.e., φ(x) vanishes outside of some interval [

a,b

The motivations underlying the term “test function” are that test functions serve as

tools in studying other functions, and that curves with certain crude geometrical

shapes, like pulses or mesas (Figs. 11.1 and 11.2), can be constructed in an infinitely

differentiable manner.

Let us now see how the idea of test functions can be used to evaluate an

unknown function of interest. Assume that a chemist needs to test the properties

of a certain substance at a fixed temperature t

. So, he gathers a batch of the stuff

with temperatures distributed in a pulse

(

T ) near T = t

. His objective is to

find some law. Mathematically speaking, the law will normally be written as a

function, say f (T). Let us see how the test function

φ is used to determine the

unknown function f.

There is no doubt that in reality some temperatures appear more often than

others. Hence,

the temperatures have a density

φ (T) supported on [a,b], and a

Figure 11.2. A mesa function supported on [

a,b].

Calculus of Generalized Numbers

337

“weighted average” is natural to consider:

Now

φ is used to measure f. If φ is chosen differently with different temperature

ranges, eventually the structure of f will be known. In the language of the chemist,

he might say that by enough experiments

φ we learn the “law” described by f.

Let ƒ : be such that

exists and is finite for any finite interval

[a,b]. Then the action of a test function φ on f is defined to be

The following result supports this example.

Theorem 11.5.1

[Richards and Youn (1990)]. Let f :

and g:

continuous and satisfy that every test function

φ has the same action on f and g.

Then f = g.

A sequence of test functions converges to zero, written if

(a)

For each

∈

the sequence of the k

th derivatives

converges

uniformly to zero.

(b)

The

have uniformly bounded supports; i.e., there is an interval [a,b],

independent of n, such that every

(

x) vanishes outside of [a,b].

Similarly,

→φmeans (φ – φ

) → 0. The set D of all test functions

together with the convergence relation, defined earlier, is called the

elementary space.

Definition 11.5.1 [Richards and Youn (1990)]. A distribution T is a mapping

from the set D of all test functions into the real or complex numbers, such that the

following conditions hold, where T (

φ) is written as

(a)

(Linearity)

for all

D and constants a and b.

(b)

(Continuity) If

then

Example 11.5.1. Let f: be piecewise continuous. For any

φ ∈ D define

It can be shown readily that T is a distribution.

338

Chapter 11

Example 11.5.2. Dirac’s δ function δ is a symbol which satisfies the following

conditions:

(11.29)

where

φ ∈ D is any test function. For a different discussion on the δ function, see

Chapter 6.

In terms of distributions, the

δ function is defined by the equation

Now shift the

δ function through a distance +a. This should give the function

(

x – a ), and

That is, the shifting

(

x – a ) evaluates the test function φ at x = a. The following

may be a little surprising:

and in general,

Let

be a sequence of distributions and T a distribution. is

convergent to T, written as T

→

T if

Based on this concept, the following theorem is interesting.

Theorem 11.5.2 [Richards and Youn (1990)]. Let f(x) be a piecewise continu-

ous function such that

Denote f

(x ) = af (

). Then

where the convergence is in the sense of distribution.

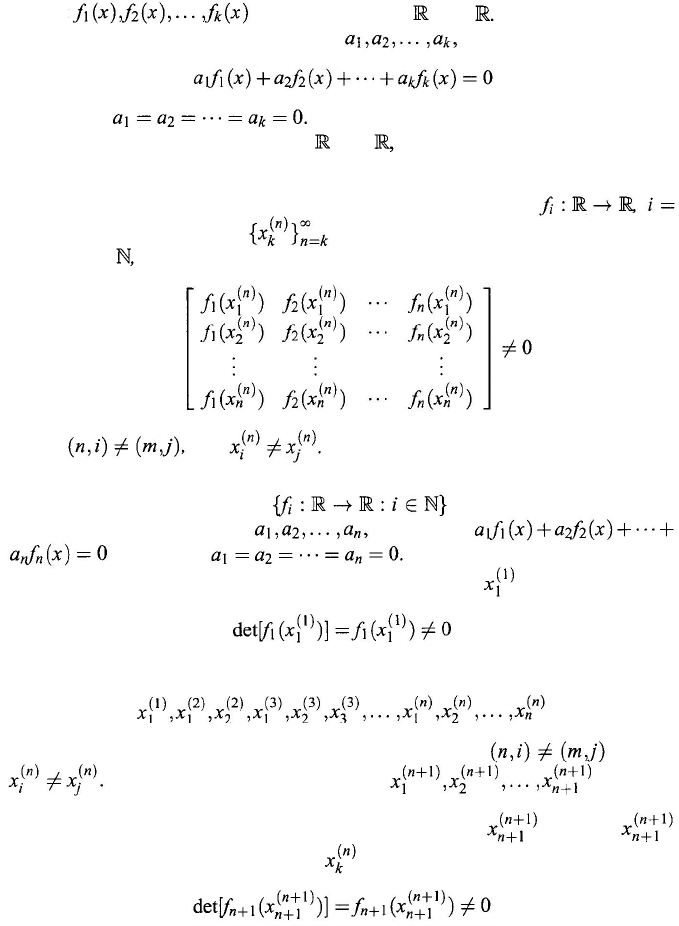
Calculus of Generalized Numbers

339

For a more comprehensive nontechnical introduction to the theory of Schwartz

distributions, refer to the splendid work by Richards and Youn (1990).

11.5.2.

GNS

Representation of Schwartz Distributions

Let

be functions from into These functions are

linearly independent if for any constants

the equation

implies that Otherwise, the functions are linearly depen-

dent. For a set F of functions from

into

F is linearly independent if each

finite subset of F contains linearly independent functions.

Lemma 11.5.1. For linearly independent continuous functions

1,2,..., there are sequences of real numbers, k = 1,2,3,..., such that

for each k

∈

det

(11.30)

and, if

then

Proof: Since the set F = is assumed to be linearly

independent for any constants

the equation

implies that

Therefore, none of the functions

in F is the zero function. Thus, there exists a real number

such that

Assume that for a natural number n, the real numbers

have been defined such that Eq. (11.30) holds and that

implies

Now we define the real numbers such that

the desired conditions are satisfied.

Since f

n+1

is not the zero function, pick a real number such that

is different from all previously chosen and that

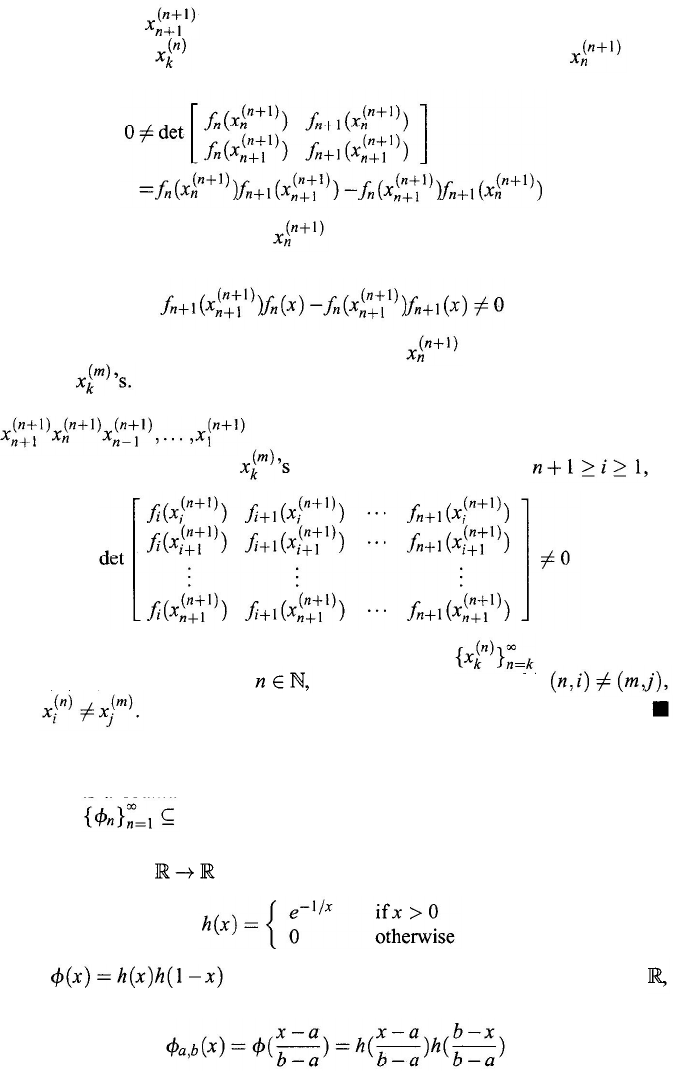
340

Chapter 11

The existence of

comes from the fact that f

n +1

is continuous and that all

previously chosen

are a finite number. Now pick a real number

such

that

The existence of such a number comes from the fact that f

and f

n +1

are

linearly independent, which implies that

The continuity of f

and

n +1

guarantees that the can be different from all

By mathematical induction it can be shown that the real numbers

can be chosen one after another so that each one

is different from all previous

and that for each i satisfying

Therefore, induction guarantees that there are sequences of real numbers,

k = 1,2,..., such that for each Eq. (11.30) holds true and if

then

Lemma 11.5.2. The elementary space D of all test functions is separable; i.e.,

there exists a countable subset F

⊆ D such that for any φ ∈ D, there exists a

sequence

F such that φ

→ φ.

Proof:

Let

: be defined by

(11.31)

Then

is a test function with support [0,1]. For any a, b

∈

define

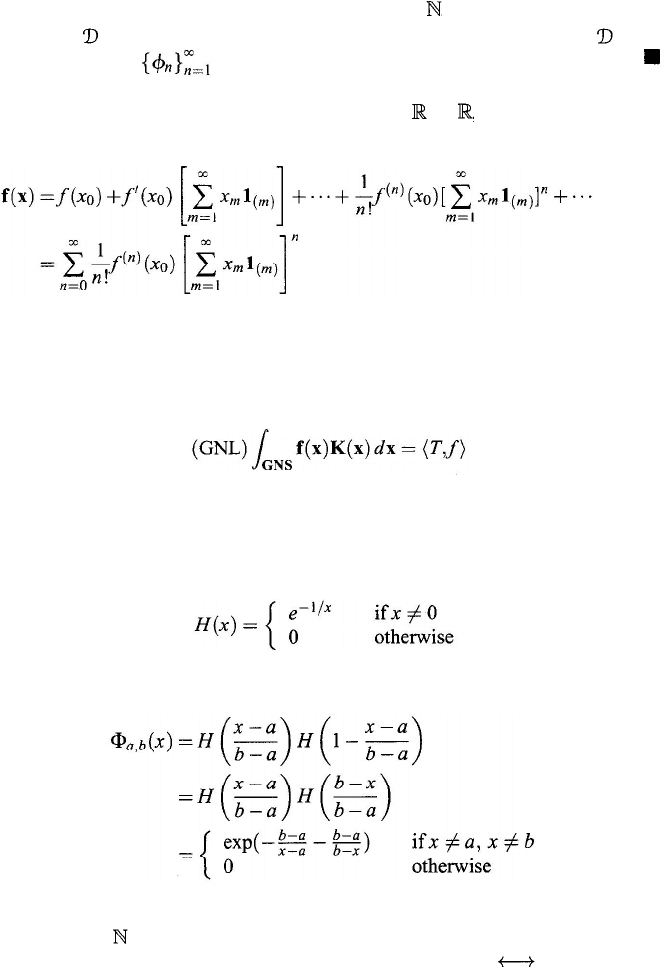
Calculus of Generalized Numbers

341

Then φ

a,b

is a test function with support [

a, b

Then

)

(

) is a test function. Let F = {p

(

)

a,b

(

) :

(

) is a polynomial

of degree

with all rational number coefficients,

∈

, and a and b are rational}.

Then

⊆

is countable. It is left to the reader to show that for any φ ∈

there

exists a sequence

⊆ F such that φ

→ φ

For each infinitely differentiable function ƒ : → , define a function f :

GNS

→

GNS

as follows:

(11.32)

Here f is called the GNS function induced by ƒ.

Theorem 11.5.3 [Wang (1985)]. Let T be a distribution and F as in Lemma

11.5.2. Then there exists K : GNS

→ GNS such that, for each ƒ ∈ F,

(11.33)

Proof: Let

For any rational numbers a and b, define

Let G = {

(

)

a,b

(

) :

(

x) is a polynomial of degree n with all rational coeffi-

cients, for

∈

, and

and

are rational numbers}. Then the families

and

can

be put into 1–1 correspondence by matching up p

(

)

a,b

(

)

(

)

a,b

(

Let p

(

)

be a polynomial of degree n with all rational number coefficients.

a,b

where

GNS

→

GNS

is induced by ƒ.

342

Chapter 11

Now we show that the family

is linearly independent. Pick an arbitrary finite

subset H ⊆ G, say

Let d

,…,d

be constants satisfying

(11.34)

It suffices to show that d

= d

...

= d

= 0.

Case 1: For each i with 1

≤ i ≤ k, assume

and that (

) ≠ (

), whenever i ≠ j. Thus, Eq. (11.34) becomes

(11.35)

Now choose k different values of x for which it is easy to evaluate the e-functions.

We obtain S, k linear equations in k variables d

, d

, … , d

, from which it can be

shown that the system has zero solution only. That is, d

= d

...

= d

= 0.

where

(

x) is defined by Eq. (11.35) satisfying (a

) ≠ (

), whenever

≠ j, and the polynomial

(11.36)

where the coefficients c

’s are rational. Equation (11.34) then becomes

(11.37)

Now group the terms of Eq. (11.37) according to the powers of x appearing in the

That completes the proof that ƒ

,ƒ

, . . .

are linearly independent.

Case 2: For each i with 1 ≤ i ≤ k, assume

polynomials P

(

x), i = 1,2

, . . . ,

k, so that each power of x appears at most once.

Calculus of Generalized Numbers

343

Equation (11.37) is true iff the coefficient of each power of x equals zero. Hence,

Eq. (11.37) is equivalent to n = max{n

, . . . ,

} + 1 many equations, each of

which looks similar to Eq. (11.35). The only difference which might occur is

that some constant coefficients may show up in front of some d

’s in Eq. (11.35).

Therefore, the argument in Case 1 implies that d

. . .

= d

= 0. That is,

,ƒ

, . . . ,ƒ

are linearly independent. This completes the proof that the family G

is linearly independent.

Since G is countable, enumerate the elements in G as

From Lemma 11.5.1 it follows that there are sequences of real numbers,

for k = 1,2,3

, . . . ,

satisfying Eq. (11.30).

(11.38)

(1)

Since

there must be a real number c

(0)

such that

(11.39)

(2) When n = 2, Eq. (11.30) is true. Hence the system

(11.40)

has a unique solution which is denoted c

(1)

and

(1)

(3)

In general, assume that for a fixed

have been defined for

k ≤ m + 1 ≤ m

+ 1. Since Eq. (11.30) holds for n = m

+ 1, the following

, k = 1,2

, . . . ,

+ 1 has A unique solution:

(11.41)

where

Choose a real-valued infinitely differentiable function

) satisfying {

∈

(

x) ≠ 0} is bounded and

(

)

dx = 1. Define a function K : GNS → GNS

as follows: for m

≥ 0,

system with unknowns

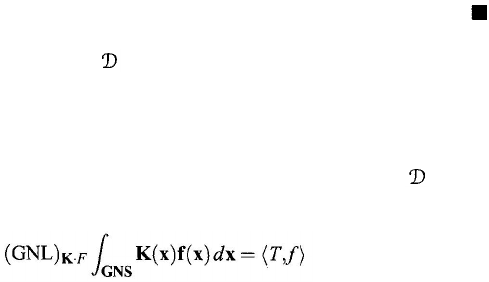
344

Chapter 11

It then follows from the definition of (GNL)-integrals and Eq. (11.41) that K :

GNS

→ GNS satisfies Eq. (11.33). This completes the proof of the theorem.

For the countable subset F

⊆ given in Lemma 11.5.2 and for the function

K : GNS

→ GNS introduced in Theorem 11.5.3, let K · F = {

:ƒ

∈

}, where

for each ƒ

∈

GNS

→

GNS

is the

GNS

function induced by ƒ; see Eq. (11.32).

Then the following result is not difficult to see.

Theorem 11.5.4 [Wang (1985)]. For each arbitrary test function ƒ

∈ of ele-

mentary space,

where T is the distribution used to determine K

11.6.

A Bit of History

Research in non-Archimedean fields has been closely related to those of

non-Archimedean topology and non-Archimedean analysis. The study of non-

Archimedean topological structures has been valuable in the study of dimension

theory and in research in algebra and algebraic geometry. To see this, one need

only to consult the p-adic topology and Stone duality theorem in Boolean alge-

bra (Nyikos and Reichel, 1975). The concept of linear uniformity, introduced

by Frechet (1945), and the theory of

-additive topological spaces, studied by

many, including Hausdorff, Sikorski (1950), Shu-Tang Wang (1964), Stevenson

and Thron (1971), Hodel (1975), Juhasz (1965), Husek and Reichel (1983), Ya-

sui (1975), and Nyikos and Reichel (1976), are related to the general study of

non-Archimedean topology. Also, non-Archimedean topology has been applied

in research of abstract distances, introduced and studied by Frechet (1946), Kurepa

(1934; 1936a; 1936b; 1956), Doss (1947), Colmez (1947), etc.

As for the study of non-Archimedean analysis, Italian differential geome-

ter Levi-Civita (1892) introduced and studied the concept of formal power

series. In particular, he discussed some algebraic problems of his non-

Archimedean field and applications in Voronese’s non-Archimedean geometry

(Voronese, 1896; Voronese, 1891), at the time criticized and not trusted by many.

The purpose of Levi-Civita’s work was to establish an extremely rigorous “arith-

metic” foundation for Voronese’s geometry. Later, Hilbert employed Levi-Civita’s

work on formal power series in his work on foundations of geometry. Hans Hahn

has been commonly recognized as the first person to study ordered algebraic

structures. In fact, his work on ordered algebraic structures is a continuation of

Levi-Civita’s formal power series. The generalized number system, introduced by