Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

294

Chapter 10

The proof is straightforward and is omitted.

Due to Proposition 10.5.2, we still use h for the mapping

⏐

and the

modeling relation

(

, h

)

: S → S', whenever no confusion occurs.

A modeling relation

h = (

: S → S'

) is called an epimorphism from the

system S into the system S' if for any fixed system S" and modeling relations h'

and h" from S' to S", h'

h = h"

implies h' = h".

Theorem 10.5.1. Let h =

(

, h

) be a modeling relation from a system S to a

system S' such that D

(

) = X, R

) = Y, D(

') = X', and R(

) = Y'. Then h is

an epimorphism from S to S' if and only if h

and h

are surjective.

Proof: Necessity. Suppose h is an epimorphism from S to S' and, without

loss of generality, the mapping

is not surjective. That is, h

(X) ≠ D (

') = X'.

There exist mappings h'

and

such that

(10.149)

where, for each arbitrarily fixed system

S''

⊂ X" × Y", h'

and

are from X' to

X".

Pick mappings

→

such that

and

= h" .

Then we

h = h"

but h' ≠ h". This contradicts the fact that h is an epimorphism from S to S'.

Sufficiency. Suppose h

and h

are surjective. Let S" be an arbitrary system

over X"

× Y" and h' = (h'

) and h" = (

, h"

) modeling relations from S' to

S" such that

h = h"

Then

(10.150)

The last implication follows because h

: X → X' is surjective and because D(

) =

X. A similar argument gives

= h". Hence, applying Proposition 10.5.2, we

have

h' = h".

That is,

is an epimorphism from

S'.



Theorem 10.5.2. Under the same assumption as in Theorem 10.5.1, if the model-

ing relation h is also surjective as a mapping (that is,

⏐

is surjective), then

h is an epimorphism. The converse is not true.

Proof: It can be clearly seen from the assumptions that the mappings h

and

are surjective. Applying Theorem 10.5.1, it follows that h is an epimorphism.

We now see an example when the converse is not true. Let

Y, S

= { (

x, x):

∈ X

= X × X, and h

= h

. Then h = (h

) is an epimorphism but

not surjective.



Systems of Single Relations

295

Theorem 10.5.3. Under the same assumption as in Theorem 10.5.1, if the mod-

eling relation h is also a relation (that is, h has a right cancellation), then h is

surjective as a mapping. The converse is not true.

Proof: Let k : S'

→ S be a right cancellation of h ; i.e., h

k = (

, id

). Let

(

x', y'

) ∈ S' be arbitrary. Then h

(

x', y') = h

(

x', y')) = (x', y'). That is, h is

surjective.

We now construct an example to show the converse may not be true. Suppose

that S

⊂ X × Y and S' ⊂ X' × Y' are systems defined by

(10.151)

and

(10.152)

Let

: D

(

S) → D

(

)

and

(

→ R(

) be two mappings defined by

If h = (

)

has a right

cancellation k =(k

, k

), we have

(

) =

or x

, k

(

) =

, and

(

) =

Case 1: Suppose that k

(

) = x

It then follows that

(

, k

) (

,y'

) = (

) ∉

S, which contradicts the hypothesis that k is a modeling relation from S' to S.

Case 2: Suppose k

(

)(

,y'

) = (x

) ∉ S,

) = x

We then have that

which contradicts the hypothesis that k is a modeling relation from S' to S. The

contradictions imply that the modeling relation

does not have a right cancellation;

i.e., h is not a retraction.



A modeling relation h from a system S to a system S' is an isomorphism from

S onto S' if h has both right and left cancellation. In this case, S is isomorphic to

S'.

Theorem 10.5.4.

A modeling relation h

: S → S' is an isomorphism from S onto

S' if and only if h is bijective from S onto S' as a mapping.

Proof: Necessity. Suppose h : S

→ S' is an isomorphism. From Theorem

10.5.3 it follows that h : S

→ S' is surjective as a mapping. It remains for us

to show that h is injective.

Let p : S'

→ S be a left cancellation of h. That is,

= (id

, id

By contradiction, suppose h : S → S' is not injective as a

mapping. There then exist distinct (

x, y

) and (

u, V ) ∈ S such that h (x, y) = h (u, v).

So, p

(

x, y) = p

(

u, v), which contradicts the assumption that p

= (id

) is the identity mapping on S.



296

Chapter 10

Figure 10.12. Properties of the mapping h from S to S' with D

(

S ) = X and R (

) = Y.

Example 10.5.1. We show that retraction does not guarantee an isomorphism.

Let S

⊂ X × Y and S' ⊂ X' × Y' be two systems defined by

(10.153)

and

(10.154)

Define a modeling relation h =

(

, h

2 ) from S to S' by letting h

(

) = h

) =

Let k = (k ) from

(

)

(

) → D

(

)

(

) be defined by

(10.155)

Then k is a modeling relation from S' to S and hk = (id

, id

). But, according

to Theorem 10.5.4, S is not isomorphic to S' because

⏐

⏐ ≠ ⏐

⏐.

Combining Theorems 10.5.2 and 10.5.3 we obtain Fig. 10.12.

A modeling relation h

= (h

, h

) from S to S' is termed as a monomorphism

from S to S' if h is injective as a mapping from S to S'. Then, similar to the

previous results, we have the following.

Theorem 10.5.5.

Under the same assumption as in Theorem 10.5.1, the following

hold:

(i)

(ii)

If both mappings h

1 and h2 are injective, then h is a monomorphism, but

the converse is not true.

If the modeling relation h is a section (that is, h has a left cancellation),

then h

and h

2 are injective, but the converse is not true.

(iii)

If h is an isomorphism, then h is a section, but the converse is not true.

Proof:

(i) If h

and

are injective, then the modeling relation h is injective

as a mapping from S to S'. Therefore, h is a monomorphism. Conversely, define

two systems S

⊂ X × Y and S' ⊂ X' × Y' such that

(10.156)

Systems of Single Relations

297

and

(10.157)

and define

by letting

and

Then h : S → S' is an injective modeling

relation, but none of the mappings h

nor

is injective.

(ii) Let be a left cancellation of

Then h

and

are injective. Conversely, define systems

⊂ X × Y and S' ⊂ X' × Y' such that

(10.158)

and

(10.159)

and define mappings h

and h

and

(

) = y'

. Then h

and

are both injective. Now if the modeling relation

h has a left cancellation k = (k

), then either

then

(10.160)

a contradiction. If

then

(10.161)

This contradicts the hypothesis that k is a modeling relation from S' to S.

(iii) We need only define two systems

⊂

and

⊂

and a section

h : S → S' such that h is not an isomorphism. Let

(10.162)

and

(10.163)

and let the modeling relation h be defined as in the proof of (ii).

Define a

left cancellation k = (k

) of h as follows:

and

But h cannot be an isomorphism from S to S' by

Theorem 10.5.4 because

Theorem 10.5.6.

A modeling relation h = (

) : S → S' is an isomorphism if

and only if h

: D

(

S) → D

(

)

and h

(

)

→

(

) are bijective.

298

Chapter 10

Proof: Necessity. Suppose h is an isomorphism. Then Theorems 10.5.3 and

10.5.5 imply that the mappings h

(

)

→ D

(

) and h

: R

(

)

→ R(

) are

surjective and injective.

Sufficiency follows from Theorem 10.5.4.

Theorem 10.5.7.

Let h

→

X' and h

→

Y' be two mappings, and S

⊂

and S' ⊂ X' × Y' be two systems. Then the product mapping h

reduces a

modeling relation from S to S'; i.e., h

2⏐

S is a mapping from S to S' if and only

if for any

Proof:

Necessity. Suppose h

2⏐

S is a mapping from S to S'. Then for any

∈ D

(

S) and any y ∈ S

(

), we have That

is, h

(

) ∈ S'

(

x )). This gives

Sufficiency. Suppose, for any

Then, for each

Therefore, h = (

) is

a modeling relation from S to S'.

From Theorem 10.5.6, it can be seen that if a system

is isomorphic to a system

S', then S' is also isomorphic to S. In fact, let h = (h

, h

) be an isomorphism

from S to S'. Then there are mappings k : Y'

→ Y such that

: X' → X and k

and (10.164)

Applying Theorem 10.5.6, it follows that k = (k

) is an isomorphism from S'

to S. Therefore, in the future we can speak about isomorphic systems.

Suppose S

⊂ X × Y is an input–output system such that D(S) = X and R

(

S) =

Y, and where I is an index set, is a covering of S;

i.e., satisfies

The collection is referred to as an

input–output system covering of S if satisfies the following two conditions:

(i)

There are coverings

of the input

space X and the output space Y, respectively.

(ii) There is a relation I

⊂

with

(

) = I

and

(

) = I

such that

and

are related by a one-to-one correspondence

ψ : Is→ I with

(10.165)

In particular, if the collections

and

are partitions of the sets S, X, and

Y, the corresponding input–output system covering of S will be referred to as an

input–output system partition. The system covering will be denoted by

Systems of Single Relations

299

A system covering will be used when viewing a system macroscopically by ig-

noring its detailed structures. Generally, not every covering is compatible with an

input–output model structure. When it is compatible, it can generate an approxi-

mation of the original input–output system. Here, the relation I

is a representation

of the approximation and will be called an associated input–output system of the

covering.

Theorem 10.5.8.

Each input–output system S

⊂

Y has an input–output system

covering, which is also an input–output system partition.

Proof: We define the collections

and

as follows:

(10.166)

The rest of the proof is clear.

Example 10.5.2. An input–output system covering (respectively, partition)

is termed a trivial covering (respectively, partition) if

⏐

= 1 or

⏐

= 1. We

now construct an input–output system S

⊂ X × Y which does not have a nontrivial

partition. Let S

⊂ X × Y be the system defined by

(10.167)

where x

∈ X and y

∈ Y are distinct elements in X and Y, respectively.

Then S may not have a nontrivial partition. In fact, by contradiction, suppose S

has a nontrivial input–output system partition Then the associated

input–output system I

⊂

× I

must satisfy

⏐

= 2 =

⏐

. In fact, if

⏐

> 2,

there is an i

∈ I

such that X

∈

contains neither x

nor x

. That is, for each

(10.168)

Equation (10.168) contradicts the condition that

and each element

is nonempty. A similar argument shows that

⏐

has to be 2.

Suppose

and

Then for each i = 1,2,

(10.169)

To guarantee that for each i = 1,2 and j = 1,2,

(10.170)

the sets X

and

must contain {

} and {

}, respectively. This fact implies

that if the input space X = {

} and the output space Y = {

}, then the

system covering would be a trivial covering, contradiction.

300

Chapter 10

When a system covering is a partition, the associated input–output system I

is characterized by the following results.

Theorem 10.5.9.

Let

and i

∈

} be an input–output system par-

tition of a system S

⊂ X × Y. Then the following holds:

and

(10.171)

where I

is the associated input–output system of the partition, X

i∈

and Y

∈

In particular, if the system I

exists, I

is unique for the given sets of and

Proof: The following is clear:

(10.172)

Suppose (i,j

)

∈

. The definition of a system covering implies that (

so there is Consequently,

Conversely, suppose there exists (

x,y ) ∈ S such

that x

∈ X

and

∈

. Since (x,y )

we have

(

x,y

)

∈

for some

∈

(10.173)

Let Since

and (

x,y

)

∈

hold, we

have x

∈ X

and

∈

. Since

and

are partitions, we must have X

= X

and

= Y

. The uniqueness of existence of the associated input–output system I

comes from the fact that

Let f: X

→ Y be a mapping from a set X to a set Y. An equivalence relation

can then be defined on X as follows:

(10.174)

The quotient set X/E

will be denoted by X/f.

Theorem 10.5.10.

Suppose that h = (h

) :

→

is a modeling relation with

(

) = X and R

(

) = Y. There then exists an input–output system partition

of S such that

and

is defined

(10.175)

A one-to-one correspondence

→ S/h

is given by

([

x],[

y]) = [(

x,y

)]

(10.176)

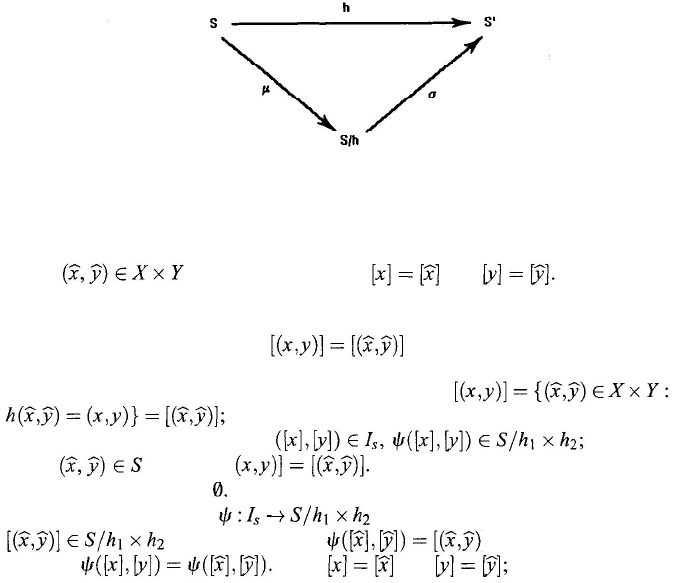
Systems of Single Relations

301

Figure 10.13. Epi–mono decomposition of a modeling relation

Proof:

We first show that the correspondence

is well defined. Let ([

x], [y]) ∈

and

be arbitrary such that

and

It suffices to

show that

(10.177)

From the definition of equivalence class, it follows that

that is,

is a mapping from

into X × Y/h

. We

now need to show that for each i.e., there

exists such that

The last equation follows from the

fact that ([

]

[

])

∩

≠

Second, we show that is a one-to-one correspondence. Let

be arbitrary.

Since

holds, ψ is surjective.

Suppose Then

and

i.e., the mapping

is injective.



Theorem 10.5.11. Suppose that S ⊂ X × Y and S' ⊂ X' × Y' are input–output

systems such that D

(

S) = X, R

(

S) = Y, D

(

) =X', and R

(

) = Y', and h =

, h

) : S → S' is a modeling relation. Let µ

: X → X/h

and µ

→

Y/h

be canonical mappings. Then the following statements hold:

(i)

µ = (µ

, µ

) is an epimorphism from S to S/h. In

particular,

µ is

surjective.

(ii)

A modeling relation σ =

(

) : S/h → S' can be defined by

([x],[y ])

(

x),

))

such that

= 1,2,

are injective.

(iii)

The diagram in Fig. 10.13 is commutative; that is, there is an epi–mono

decomposition of h.

(iv)

If h

and h

are injective, then the modeling relation µ is an isomorphism.

(v)

If h is surjective, then σ is an isomorphism.

302

Chapter 10

Proof: (i) It is clear that the canonical mappings µ

: X → X/h

and µ

Y → Y/h

are surjective when defined by µ

(m) = [m] for i = 1, 2. If (x, y) ∈ S,

(

x, y) ∈ ([x] × [y

])

∩

S, and thus µ(x, y) = (µ

(

x), µ

(

y)) = ([x], [y]) ∈ S/h. By

Theorem 10.5.1, the modeling relation µ is an epimorphism. Since there is

(

x',y'

) ∈ S for any ([x

], [

])

∈

S/h

such that [

] = [x] and [

] = [y

], µ is surjective.

(ii) Since [x] = [

] implies is well defined.

The mapping

is also well defined. Suppose ([x], [y]) ∈ S/h. Then the definition

of S/h implies there exists

such that

Consequently,

and

Hence, σ is a modeling relation, and σ

and σ

are clearly injective.

(iii) The commutativity of the diagram in Fig. 10.13 is clear from the definitions

of µ and σ.

(iv) If

and

are injective,

says that µ

is injective. Similarly,

the mapping µ

is also injective. From statement (i) and Theorem 10.5.6, we know

that µ is an isomorphism.

(v) The desired result can be shown as in the proof of (iv).

Suppose

is a system,

is a collection

of systems, and S

⊂ X × Y satisfies the conditions



(10.178)

and

(10.179)

where we identify each element

with

The system S is called a surjective complex system representation of

with

order

if there exist mappings

and

such that

S is called an injective complex system representation of with order n if there

exist mappings

and

such that ⊂ S and k

and

are injective. S is called an isomorphic complex system representation of

with

order n if there exist mappings

and

such that

is an isomorphism from S onto S'.

Proposition 10.5.3. For each system and each natural number n > 0,

has a surjective, an injective, and an isomorphic complex system representation

with order n.

Proof: Let and be the diagonals of the product sets, respec-

tively. That is,

(10.180)

Systems of Single Relations

303

We now define S ⊂ X × Y by letting

(10.181)

and define mappings

and

Then we have the desired results with respect to (

, h



Theorem 10.5.12.

A system

has an injective complex system repre-

sentation S with order n over a class of systems iff

there exist n partitions of for each i = 1, 2,. . . , n, such

that the following conditions hold:

(i)

(ii)

(iii)

is an input–output system partition of

, for each i =

1,2, . . . ,

where

is an

associated input–output system of P

with

1 i

and σ

2 i

injective.

There exists an embedding

Let and

be the input and output

spaces of respectively, where and are partitions by definition and

[

]

and [y

]

are equivalence classes of

and

, respectively. Then, for

arbitrary

and

for each i =

1,2, . . . ,

(10.182)

and

(10.183)

Proof:

Necessity. Let

⊂

be an injective complex system representation

with order n, where

⊂

1 × X

. . . ×

and

Y ⊂

. . .

Let

be the projection defined by Eq. (10.96). Then

Πi

→

is a modeling relation. Let be an injective modeling

relation. Since

is a modeling relation, we can

define a partition

(10.184)

We now check the conditions (i)–(iii) for these partitions

, i = 1, 2, . . . ,n. Since

Theorem 10.5.10 implies that P

is an input–output system partition, condition

(i) holds. Since the associated input–output system

is given by