Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

284

Chapter 10

From the hypothesis that S is injective, it follows that x = w,

that is,

Hence, S

is bijective.



Proposition 10.4.6.

Suppose that S

⊂

Y is a functional linear time system that

S has been decomposed into a family of component systems

such that S is noninteracted; i.e., If S is time invariably

realizable, each component system S

is then also time invariably realizable.

Proof: From the hypothesis that S is a functional system from X into Y, it

follows that

(S) ⊂ X. Thus, from the proof of Proposition 10.4.4, for each fixed

∈ I, D(S

) =

We now let t ∈ T and x

∈ X

be arbitrary. There exists an element

∈ X such

that

Since

is time invariably realizable, from Eq. (10.76) it follows

that for t ∈ T,

(10.103)

Let

Then x

∈ A ≠

and each x ∈ A satisfies

Eq. (10.103), which implies that

(10.104)

Therefore,

(10.105)

Applying Eq. (10.76), we complete the proof that

is time invariably realizab1e.



The following result combines Propositions 10.4.1–10.4.6.

Systems of Single Relations

285

Theorem 10.4.1.

Let S

⊂

Y be an input–output system which has been decom-

posed into a family of factor systems

such that

Then the following statements hold:

(1) S is a linear system if and only if each S

is a linear system.

(2) S is a linear time system if and only if each S

is a linear time system.

(3) S is strongly stationary if and only if each S

is strongly stationary.

(4) S is causal if and only if each S

is causal.

(5) S is bijective if and only if each S

is bijective.

(6)

The functional system S is time invariably realizable if and only if each S

is functional and time invariably realizable.

The proof is not hard and is left to the reader.

Theorem 10.4.1 shows that the theoretical properties of many important sys-

tems are either hereditary from the overall system S to each component system S

or able to be lifted up from S

to S. In practice, we always hope to study S by

studying each component system

Let S ⊂ X × Y be a linear system. We say that S can be decoupled by feedback

if there exists some functional system

∈

such that

(10.106)

where it is assumed that

is the projection defined by relation (10.96).

The concept of decoupling by feedback shows the following actions: The

original system S may not be noninteracted, so there might be some properties

which cannot be lifted up from component systems to the overall system S. If S is

decoupled by feedback, after applying appropriate feedback transformation, S is

transformed to a system which has a noninteracted complex systems representation.

We now can use that representation to analyze and control S.

Theorem 10.4.2.

Suppose that S

⊂

Y and S

: Y → X are a linear system and

a functional linear system, respectively, such that S is decomposed into

and S

is decomposed into

Then, for each i ∈ I,

(10.107)

286

Chapter 10

Proof:

For each

there exists (x,y

)

∈

(

S,S

) such that

(x ,y) = (

). Since, it follows that

(10.108)

Equation (10.108) implies that

That is,

Let

be arbitrary. There then exists (x,y) ∈ S such that

(10.109)

Therefore,

From this, we have

(10.110)

Equation (10.110) gives



Theorem 10.4.3.

Assume the Axiom of Choice. Suppose that S

⊂

Y is a linear

system that can be decomposed into a family of component systems

= {

: i ∈ I

Then S can be decoupled by feedback if and only if R

(

S) = Π

{

(

) : i ∈ I } and

(

S) =

{

(

) :

∈

Proof:

Necessity. Suppose S can be decoupled by feedback. By the definition

of decoupling by feedback, there exists a functional linear system S

∈

such

that

(10.111)

Systems of Single Relations

287

Therefore, by Theorem 10.2.5,

(10.112)

and

(10.113)

Sufficiency. Let S'

⊂ X × Y be the system defined by

(10.114)

Since and

due to our assumption,

we see that R(S) = R

(

) and N

(

S) = N

(

). By applying Theorem 10.2.5, we

find there exists a functional linear system S

∈

such that

(10.115)



That is,

can be decoupled by feedback.

Example 10.4.2. As an example of decoupling by feedback, consider the multi-

variable system S defined by

= Az + Bx

y = Cz + Dx

(0) = 0

(10.116)

where z is an m × 1 variable vector, A an m × m constant matrix, B an m × n

constant matrix, C an n

× m constant matrix, D an n × n nonsingular constant

matrix, and

is piecewise continuous}

(10.117)

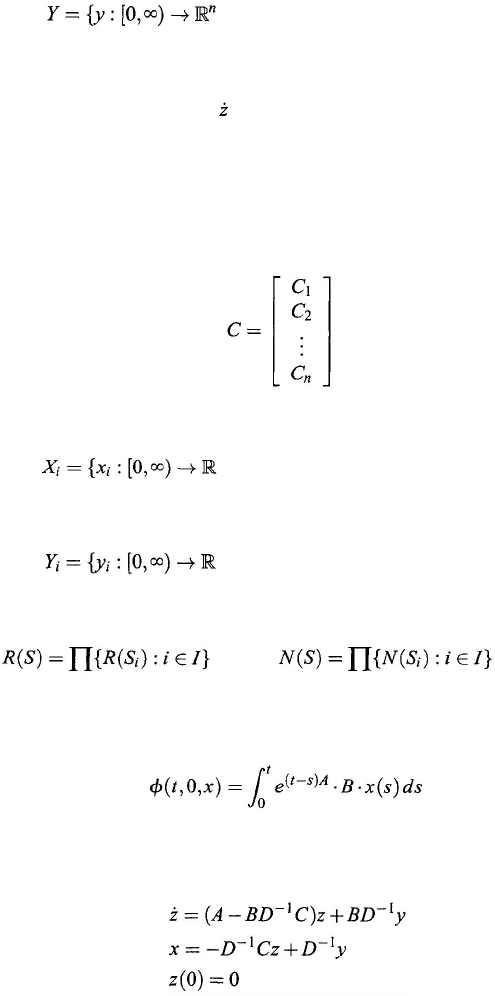
288

is the input space and

: y is piecewise continuous}

is the output space. For each

= 1, 2, . . . ,

define the system

= Az+B

= C

z(0) = 0

Chapter 10

(10.118)

(10.119)

where

is an m × 1 constant matrix such that B = [B

. . . B

], C

is a 1 × m

constant matrix such that

is a nonzero constant, and

: x

is piecewise continuous}

is the input space and

: y

is piecewise continuous}

(10.120)

(10.121)

(10.122)

is the output space. Then the systems

and

, i = 1, 2, . . . , n, satisfy

and

(10.123)

In fact, for any x ∈ X, the solution of the differential equation (10.116) in S is

given by

(10.124)

Thus,

(

S) = X. At the same time, since the matrix D is nonsingular, the inverse

system

–1

is obtained as follows:

(10.125)

Systems of Single Relations 289

Therefore, a similar argument shows that R

(

S) = D (

–1

) = Y. For the same

reason, we can show that for each

= 1, 2, . . . ,

n, R

) = Y

. That is,

For the null spaces of the systems S and S

, i

= 1, 2, . . . ,

(10.128)

Therefore,

(

S) = Π{N( S

) : i = 1, 2, . . . , n }. By Theorem 10.4.3, S can be

decoupled by feedback. In fact, define

(10.126)

(10.127)

and

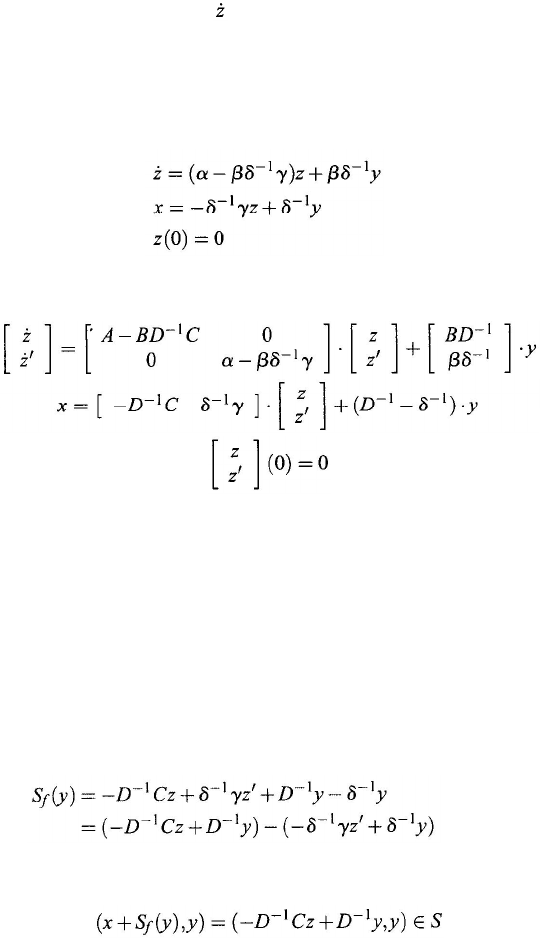
290

Chapter 10

Then the system

= S

× S

. . .

is represented by

= α

z +

βx

z +

δx

z (0)=0

Since

is nonsingular,

–1

is obtained as follows:

(10.129)

(10.130)

If we define a functional linear system

: Y → X as follows:

(10.131)

Then the original system S can be transferred into S

by this feedback component

system

. In fact, for any pair (x,y) ∈ X × Y, (x,y

)

∈

iff the input x and the

output

satisfy the systems representation in Eq. (10.130) iff (

x + S

(y), y) ∈ S.

We show the last “if and only if” condition as follows.

First, suppose that the input x and the output y satisfy the systems represen-

tation in Eq. (10.130). Let z' be the solution of the differential equation in the

representation in Eq. (10.130), and let z be the solution of the differential equa-

tion in the systems representation in Eq. (10.125). Then [

zz']

is the solution of

the differential equation in the systems representation in Eq. (10.131). From the

definition of

, it follows that

(10.132)

Therefore,

(10.133)

where the membership relation comes from the systems representation in

Eq. (10.125) of the inverse system

–1

Systems of Single Relations

291

Second, suppose that a pair (

x, y) ∈ X × Y satisfies (x + S

(

), y) ∈ S. From

the systems representations in Eqs. (10.125) and (10.131), we have

(10.134)

That is,

(10.135)

Combining Eq. (10.135) with the systems representation in Eq. (10.130) proves

that the pair (x, y) satisfies the systems representation in Eq. (10.130).

10.5. Decomposability Conditions

Intuitively speaking, a complex system consists of several subsystems (see,

for example, Sections 9.3 and 9.6). Let us first consider the following example.

Suppose that

(10.136)

for

= 1, 2, 3, are three input–output systems such that

1, 2, 3 if and only if

and

Suppose these three systems are connected in series; that is, x

= y and x

= y

hold; furthermore, suppose

and

are the input space and the output

space of a new system , defined as

(10.137)

Then

is the composition of

, and

. However, in Eq. (10.137), the

component systems

, S

, and S

completely disappeared.

Let us now consider another construction of a new system S. We let

(10.138)

and the new system S ⊂ X × Y is defined by

(10.139)

Figures 10.10 and 10.11 show the geometric meanings of

and S. The system

S is a representation of the whole system, which explicitly reflects the fact that

∈

, i =

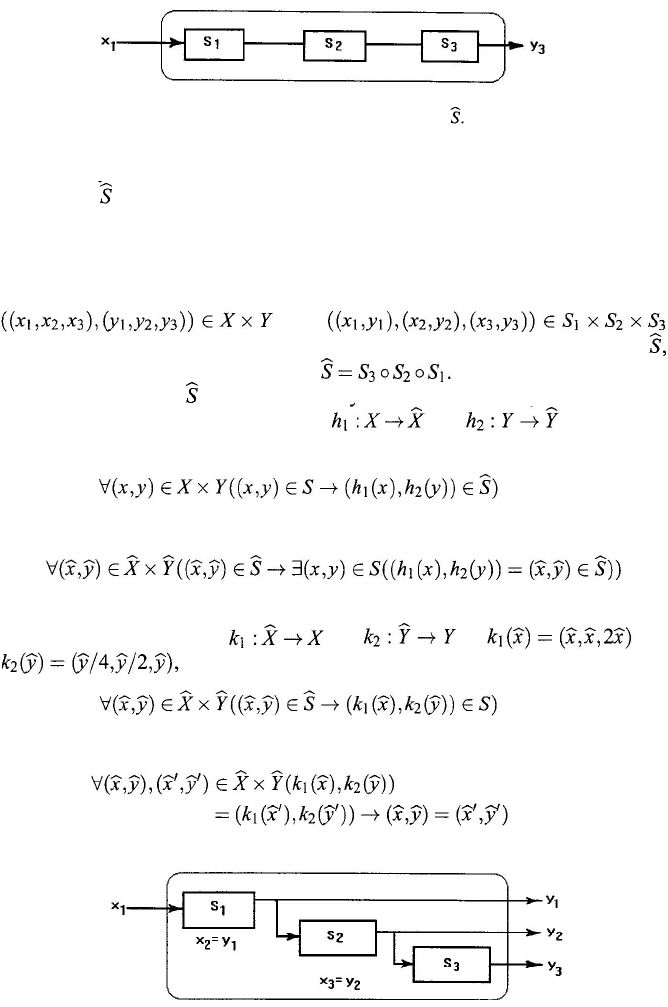
292

Chapter 10

Figure 10.10. Structure of the system

the whole system is composed of three component systems S

, i = 1, 2, 3. The

structure of

is called a global system representation of the whole system, while

S is a complex system representation of the whole system. In fact, S is the product

system of S

= 1, 2, 3.

The complex system S is defined over X and Y, but to emphasize

fact that S consists of the component systems S

, S

, and S

, we identify

with

and denote the complex system S by S

⊂ S

× S

. For the global system

we emphasize the structure by writing

The global system

and the complex system S are intimately related to each

other. In fact, if we define two mappings

(10.140)

and

(10.141)

If we define two mappings

and

then k

and k

satisfy the relations

(10.142)

and

(10.143)

Figure 10.11. Structure of the system S.

by h

(

and

) = x

and

) = y

, then

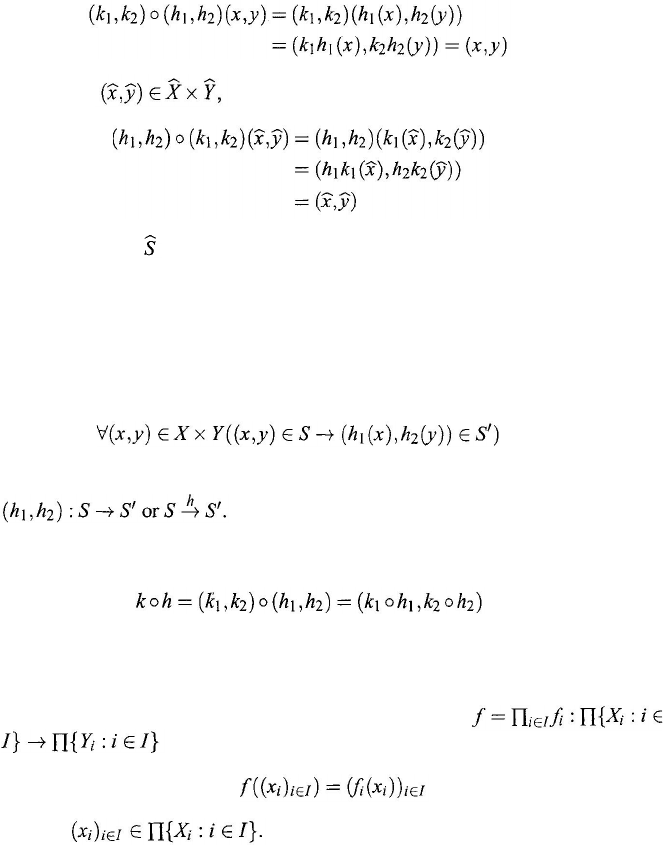
Systems of Single Relations

293

Combining relations (10.140)–(10.143), we can see that for any

(x, y) ∈ X × Y

(10.144)

and for any

(10.145)

Therefore,

and are similar.

Generally, let S ⊂ X × Y and S' ⊂ X' × Y' be two input–output systems, and

, i = 1, 2, be mappings such that

: X → X' and

→

(10.146)

satisfying the condition

(10.147)

Then h =

(

, h

) is called a modeling relation from S to S' and is denoted by

Notice that h is actually a mapping from S into S'.

Proposition 10.5.1. Suppose that h = (

) and k = (

) are modeling re-

lations from system S

to system S

and from S

to system S

, respectively. Then

the composition

is a modeling relation

from S

to S

The proof is straightforward and is omitted.

: i ∈ I} are families of sets and that {

: X

→

: i ∈ I} is a family of mappings. The product mapping

is defined by

(10.148)

for any

When I = {1, 2, . . . , n} is finite, we denote the

product mapping ƒ by

…

. The following result shows the relation

between the concept of modeling relations and that of product mappings.

and

k = (

) are two modeling

relations from system S to system S'. Then the restriction of the product mappings

Suppose {X

: i ∈ I} and {

Proposition 10.5.2. Suppose that h = ( h

)

× h

and

on S are mappings from S to S'. Furthermore, if D(

) = X

and R

(

) = Y, then h

⎥

S = k

⎥

if and only if h

, i = 1, 2.