Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

254

Chapter 9

Theorem 9.7.12.

Suppose that

{

S, l

, T

} is a linked α

-type hierarchy of systems

in the category such that for some index t

∈ T, the state S

(

)

generally controllable on V' relative to a mapping

Then

the inverse limit lim

←

{S, l

, T

} is also generally controllable (but relative to a

diffrent mapping G

Proof:

From Theorem 9.6.5 it follows that we need only show that the mapping

is S-continuous. Theorem 9.7.1 implies this.

9.8. References for Further Study

The search for an ideal definition of general systems has been going on for

decades: see von Bertalanffy (1972), Mesarovic and Tahakara (1975), Gratzer

(1978), Klir (1985) and Lin (1987). The study of time systems can be found

in many publications. For example, Schetzen (1980) studied continuous time

systems of multilinearity; Rugh (198 1 ) gave a systematic theory on nonlinear

continuous and discrete time systems; a more general setting of the concept of

time systems can be found in Mesarovic and Takahara (1975), and their definition

was generalized by Ma and Lin (1987).

The constructions of new systems, such as free sum, products and limit sys-

tems, were first given by Ma and Lin (1987; 1987; 1988d). Studies on various

controllabilities of systems can be found in almost all books on systems. For

example, Deng (1985) studied the concept of gray control, Wonham (1979) pre-

sented a concept of controllability of linear systems of differential equations, and

a study of controllabilities of nonlinear systems can be found in (Casti, 1985).

Not all of the concepts of controllabilities are equivalent. The concepts of con-

trollabilities presented here are based on research contained in (Mesarovic and

Takahara, 1975; Ma and Lin, 1987). Periodic and order structures of families of

systems were studied intensively in (Lin, 1988b; Lin, 1989a). Connectedness and

S-continuity were first studied in (Lin, 1990c; Ma and Lin, 1990e). Cornacchio

(1972) showed what an important role the concept of continuity played in research

of general systems theory and its impacts on engineering, computer science, social

and behavioral sciences, and natural sciences.

CHAPTER 10

Systems of Single Relations

As studied in Chapter 9, a (general) system consists of a set of objects and a

set of relations between the objects. In practice, many systems, which can be

described by one relation, have many complicated structures and properties that

we still do not completely understand. In this chapter, we concentrate on systems

of one relation and related concepts. Section 10.1 is devoted to the study of

two very new concepts: chaos and attractor. The second section contains the

general concept of linear systems and characterizations of feedback systems, and

the following section introduces important concepts, including MT-time systems,

linear time systems, stationary systems, and time invariably realizable systems,

and study some feedback-invariant properties. Section 10.4 shows how “whole”

systems can be decomposed into factor systems by feedback, and an example is

given. Section 10.5 studies the conditions under which “whole” systems can be

decomposed.

10.1. Chaos and Attractors

A system S = ( M, {r }) is called an input–output system if there are nonzero

ordinal numbers n and m such that

(10.1)

Without loss of generality, we let X = M

and Y = M

; instead of using the

ordered pair (

{

}), we will think of S as the binary relation r such that

(10.2)

where the sets X and Y are called the input space and the output space of S,

respectively. In the real world, most systems we see are input–output systems. For

example, each human being and each factory are input–output systems.

If we let Z = X

∪ Y, the input–output system S in Eq. (10.2) is a binary relation

on Z. Let D

⊂ Z be an arbitrary subset. If D

∩ S = then D is called a chaos of

255

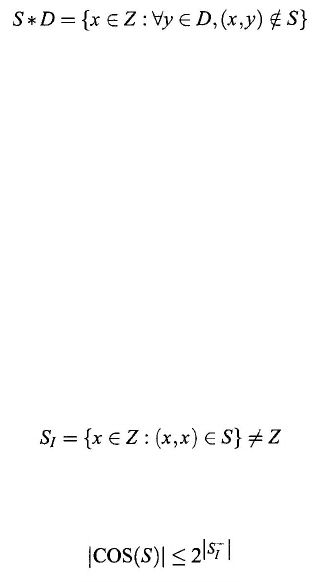
256 Chapter 10

S. Intuitively, the reason why D is known as a chaos is because S has no control

over the elements in D.

Theorem 10.1.1. The necessary and sufficient condition under which an input–

output system S over a set Z has a chaotic subset D

≠ Ø, is

S is not a subset of I

(10.3)

where I is the diagonal of the set Z defined by I = {(x,x) : x

∈ Z

Proof: Necessity. Suppose that the input–output system S over the set Z has a

nonempty chaos

Then

D²

∩

Ø.

Therefore, for each

∈

(

d, d

) ∉ S. This

implies that S

⊄ I.

Sufficiency. Suppose that (10.3) holds. Then there exists d

∈ Z such that

(

d, d) ∉ S. Let D = {

}. Then the nonempty subset D is a chaos of S.



Let S ⊂ Z

² and define

(10.4)

where D

⊂ Z.

Theorem 10.1.2. Let D

⊂ Z. Then D is a chaos of the system S iff D ⊂ S

Proof: Necessity. Suppose D is a chaos of S. Then for each object d

∈ D and

any y

∈ D,

(

d,y) ∉ S

(10.5)

Therefore,

∈

D. That is, D

⊂ S

Sufficiency. Suppose

satisfies

⊂

Then

∩

S = Ø. Therefore, D is

a chaos of S.



Let COS(S) denote the set of all chaotic subsets on Z of the input–output

system S. If S

⊄ I, then

(10.6)

We denote the complement of S

by S

–

= Z – S

. Then Theorem 10.1.1 implies

that each chaos of S is a certain subset of S

–

. Therefore,

(10.7)

The following theorem is concerned with determining how many chaotic sub-

sets an input–output system has.

Systems of Single Relations

257

Theorem 10.1.3. Suppose that an input–output system S ⊂ ⊂ Z

satisfies the fol-

lowing conditions:

(i)

S is symmetric, i.e.,

(

x, y) ∈ ∈ S implies (y,x) ∈ ∈ S,

(ii)

S is not a subset of I,

(iii)

and

(iv) there exists at most one such that either

(

x,y) ∈ ∈ S or

(

y,x) ∈ S.

Let Then

(10.8)

where k = n

/2.

Proof:

According to the discussion prior to the theorem, it is known that every

chaotic subset of Z is a subset of S

–

. The total number of all subsets of

–

is 2

Under the assumption of this theorem, a subset of

–

is a chaos of S if the subset

does not contain two elements of S

–

which have

-relations. Among the elements

of S

–

, there are

/2 pairs of elements with S

-relations, and every two pairs do not

have common elements. Let {

x, y} be a pair of elements in S

–

with an S

-relation,

then every subset of

–

{

x,y

}

∪

{

x,y

}

forms a subset of S

–

not belonging to

COS(

S). There are a total of 2

m –2

of this kind of subset. There are n/2 pairs of

elements in S

–

with S

-relations, we subtract these (

/2) × 2

m –2

subsets from the

subsets of S

–

. But, some of the (

) × 2

m –2

subsets, them are in fact the

same ones. Naturally, every subset of S

–

, containing two pairs of elements in

–

with S-relations, has been subtracted twice. There are such sets. We

add the number of subsets which have been subtracted twice, and obtain

(10.9)

However, when we add subsets, the subsets of

–

containing three pairs

of elements of S

–

with S-relations, have been added once more than they should

have. Therefore, this number should be subtracted. Continuing this process, we

258

Chapter 10

have



By using the same method, the constraint in Theorem 10.1.3 that the system S

is symmetric can be relaxed.

Theorem 10.1.4. Suppose that an input–output system S

⊂ Z² satisfies conditions

(ii)–(iv) of Theorem 10.1.3. Let n =

and k = n/2. Then

(10.10)

Let

be an input–output system on a set

A subset

⊂

is called an attractor

if for each

where

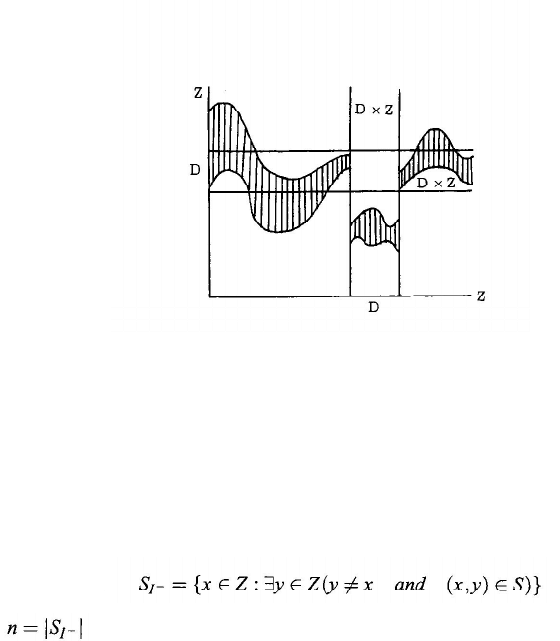
Figures

10.1 and 10.2 show the geometric meaning of the concept of attractors. When S is

not a function, Fig. 10.1 shows that the graph of S outside the vertical bar D × Z

overlaps the horizontal bar Z × D. When S is a function, Figure 10.2 shows that

the graph of S outside the vertical bar D × Z must be contained in the horizontal

region Z × D.

Theorem 10.1.5. Suppose that S

⊂ Z² is an input–output system over the set Z

and D

⊂ Z. Then D is an attractor of S, iff D ⊃ S

Proof: Necessity. Suppose that D is an attractor of S. Let d

∈ S

D be an

arbitrary element. By Eq. (10.4), for every x

∈ D, (

d,x

) ∉ S. Therefore, d ∈ D.

That is, S * D

⊂ D.

Systems of Single Relations

259

Figure 10.1. D is an attractor of S, and S

(

) contains at least one element for each x in Z – D.

Sufficiency. Suppose that D satisfies D ⊃ S

D. It follows from Eq. (10.4)

that for each object x

∈ Z – D, x ∉ S

D, so there exists at least one object d ∈ D

such that (

d,x

) ∈ S. That is,

(

∩

≠

This implies that D is an attractor of



Theorem 10.1.6. The necessary and sufficient condition under which an input–

output system S

⊂ Z² has an attractor D ⊂ Z is that S is not a subset of I.

≠

Proof: Necessity. Suppose S has an attractor D such that D ⊂ Z. By contra-

≠

diction, suppose S ⊂ I. Then for each D ⊂ Z, Z – D ⊂ S

Therefore, when

Z – D ≠ D ⊄ S

D; i.e., S, according to Theorem 10.1.5, does not have any

attractor not equal to Z. This tells that the hypothesis that S has an attractor D

such that D

⊂ Z implies that S ⊄ I.

≠

Figure 10.2. D is an attractor of S, and S is a function from Z to Z.

260

Chapter 10

Figure 10.3. D is a strange attractor of the system S.

Sufficiency. Suppose S ⊄ I. Choose distinct objects x,y ∈ Z such that (x,y) ∈

S, and define D = Z – {x}. Then, according to Eq. (10.4), D ⊃ S

D. Applying

Theorem 10.1.5, it follows that S has attractors.



Theorem 10.1.7. Suppose that an input–output system S ⊂ Z² satisfies the con-

dition that if

(

x,y) ∈ S then, for any z ∈ Z, (y,z) ∉ S. Let

(10.11)

and

ATR(

S) be the set of all attractors of the system S. Then

⏐

ATR (

)

⏐

= 2

(10.12)

Proof: For each subset

⊂

–,

let D

= Z – A.

Then

⊃ S * D

. In

fact, for each object

∈

(d,x

)

∉

for every x

∈ D,

. Therefore, d ∉ A.

Otherwise, there exists an element y

∈ Z such that y ≠ d and (

d,y

) ∈ S.

The

hypothesis stating that if (

x,y) ∈ S then for any z ∈ Z, (y,z) ∉ S, implies that the

element

∈

–

contradiction; so

∈

–

. This says that

⊃ S

Applying Theorem 10.1.5, it follows that the subset

is an attractor of S. Now

it can be seen that there are 2

many such subsets D

in Z. This completes the

proof of the theorem.



A subset D ⊂ Z is a strange attractor of an input–output system S ⊂ Z² if D is

both a chaos and an attractor of S. Figure 10.3 shows the case when a subset D

of Z is a strange attractor of an input–output system S, where the square D × D is

the only portion of the band Z × D over which the graph of S does not step.

Theorem 10.1.8. Let D

⊂ Z. Then D is a strange attractor of the input–output

system S iff D = S

Systems of Single Relations

261

The proof follows from Theorems 10.1.2 and 10.1.5.

Theorem 10.1.9. Suppose that S ⊂ Z

is an input–output system and D ⊂ Z. Let

us denote

(10.13)

Then the following statements hold:

(i) D is a chaos of S iff D

⊂ Z – SD.

(ii) D is an attractor of S iff D

⊃ Z – S

(iii) D is a strange attractor of S iff D = Z – S

Proof: It suffices to show that S

D = Z – S D. Let x ∈ S

D be an

arbitrary element. Then for any element y

∈ D, (x,

) ∉ D. Thus, x ∉ S

; i.e.,

∈ Z – S D. If an element x ∉ S

D, there exists at least one element y ∈ D

such that (x

)

∈

S. This implies that x ∈ SD; therefore, x ∉ Z – SD. This

completes the proof that S

D = Z – SD. The rest of the proof of the theorem

follows from Theorems 10.1.2, 10.1.5, and 10.1.8.

of input–output systems.

We conclude this section with a discussion of the existence of strange attractors

Theorem 10.1.10. Suppose that S ⊂ Z

is a symmetric input–output system. Then

a necessary and sufficient condition under which there exists a strange attractor

of the system S is that there exists a subset D

⊂ Z such that D

∩ S = ø and for

each x

∈

∩

)

≠ ø.

Proof: Necessity. Suppose S has a strange attractor D. From the definition,

it follows that D

∩ S = ø . At the same time, if there exists an element x ∈ S

satisfying

∩

(

x) = ø then x ∈ S

D. By Theorem 10.1.8, x ∈ D. However,

∈ S

, we must have x ∉ S

{x}, which implies that x ∉ S

D. This leads to a

contradiction.

Sufficiency. Suppose there exists D ⊂ Z such that D

∩ S = ø and for each

∈ S

, D

∩

(

x) ≠ ø. Let be the collection of subsets of Z defined by

and

(10.14)

Since D

∈ is not empty. It is clear that for each linearly ordered subset

, ordered by inclusion, is also contained

. Therefore, contains all maximal elements under the order relation of

inclusion.

262

Chapter 10

Let

be a maximal element in . By Theorem 10.1.2, it follows that

⊂

If B

≠ S

B, pick an element x ∈ S

B – B and define

(10.15)

According to the definition of the element

, for each y ∈ B, (x

) ∉ S. From the

hypothesis that S is symmetric, it follows that (

)

∉ S for every y ∈ B. Besides,

since for each

for each A

∈

, we have

; i.e.,

∉ S

. Therefore,

. This contradicts the assumption that B is a

maximal element in

We next discuss the conditions under which a composition of input–output

systems has strange attractors.

Theorem 10.1.11. Suppose that ƒ and g are two input–output systems on a set Z

such that

Then a necessary and sufficient condition under which

the composition system g f has a strange attractor is that there exists a subset

⊂ Z such that the following conditions hold:

(i)

(ii) For every

is not a subset of (Z

–

)(x

Proof: Applying Theorem 10.1.10, the composition system gf has a strange

attractor if and only if there is a subset D

⊂ Z such that

′

)

(ii

′

) For each

It now suffices to show that (a) conditions (i) and (i’) are equivalent and (b)

conditions (ii) and (ii’) are equivalent.

Proof of (a). Condition (i’) is true iff for any x

∈

, (x

)

∉

f , iff there

does not exist a z

∈ Z such that (x,z

)

∈

and (

z ,y

)

∈

, iff for any x ∈ D and any

; i.e., (i) holds.

Proof of (b). condition (ii’) holds iff for each x

∈ (g f

)

there exists d ∈ D

such that (x

) ∈ g f, iff for each x ∈ (g f

)

there exist d ∈ D and z ∈ Z such

that (x

)

∈

and (

)

∈

ƒ, iff for each

∈

(

)

there exists

∈

D such that

)

∈

, iff for each x ∈ (

)

there exists z ∈ fD such that (x

z) ∉ Z–g

;

iff for each

; i.e., (ii) is true.

Systems of Single Relations

263

10.2. Feedback Transformations

Let

such that

be a field, X and Y linear

spaces

over

, and S an

input–output

system

(i) ø

≠ S ⊂ X × Y.

(ii)

∈

and

∈

implify

∈

(iii) s ∈ S and α ∈

implify

∈

Here + and · are addition and scalar multiplication in X × Y, respectively, and

defined as follows: For any (x

), (

) ∈ X × Y and any α ∈

(10.16)

(10.17)

The input–output system S is then called a linear system.

Theorem 10.2.1. Suppose that X and Y are linear spaces over the same field

Then the following statements are equivalent:

(1)

S ⊂ X × Y is a linear system;

(2)

There exist a linear space C over

and a linear mapping

ρ : C × D

(

S) → Y such that (x,y) ∈ S iff there exists a c ∈ C such that

(

) = y.

(3)

There exist a linear space C over

and linear mappings R

: C → Y and

(

→ Y such that the mapping ρ in (2) is such that

(

) = R

(

) +

(

x) for every (

) ∈ C × D

(

Here D

(

S) is the domain of the input–output system S.

Proof: First, the domain D

(

S) is a linear subspace of the space X. For any

∈

(

) and any

α ∈

, there exist y

∈ Y such that (x

) , (

) ∈ S.

From the hypothesis that S is linear, it follows that

(10.18)

and

(10.19)

and thus x

+ x

and

∈ D(S).