Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

244

Chapter 9

Then there exists a linked time system such that each state is a

nondiscrete input–output system and is v-controllable relative to some mapping

Proof: First we see the construction of the linked time system B y

AC we well-order the time set T

, . . . ,

⏐

(9.209)

where t

is the initial element in T. Suppose that the original order on T is ≤, and

in Eq. (9.209) T is well-ordered by a well-order relation

≤ * . Generally, ≤ and

are different.

Define

Suppose that for some

⏐T⏐ the system

and the mappings

have been defined such that

for each

k <

α and any i, r, j < α such that

Now define

and

and and

as follows: Let E

be the equivalence

relation on the object set

defined by

and

(9.210)

where

and

For each β < α

if t

, define

(9.211)

for each

where

, we define

(9.212)

for each

where

It is then not hard to prove

that

is a family of linkage mappings.

By transfinite induction, a linked time system

is defined such that

and each state

is a nondiscrete input–output system with input space

and output space

Second, we show that each state is v-controllable relative to some mapping

(9.213)

Let Dom

and Ran

For any x

∈

Dom(

) there

exists

∈

Dom (

) such that

(9.214)

General Systems: A Multirelation Approach

245

where cg

is a control function of

. Thus, there exists a

∈

Ran(

) such that

(9.215)

Let

and

If we assign

then

(9.216)

and

Therefore, the sys-

tem

is v

-controllable relative to the mapping

Theorem 9.6.11. Assume hypotheses (a)–(c) of Theorem 9.6. 10 and that S

controllable on V’

⊂

V relative to a mapping G

: Dom (

) × Ran (Yt

)

→

V. Then

there exists a linked time system

such that each state

is a nondiscrete

input–output system and is controllable on V' relative to some mapping G

The proof is a slight modification of that of Theorem 9.6.10 and is omitted.

Theorem 9.6.12.

Assume hypotheses (a)–(c) of Theorem 9.6.10 and that S

is col-

lectively controllable on V

⊂

V relative to a mapping G

: Dom (

)

Ran (

)

→

V. Then there exists a linked time system such that each state Q

is a

nondiscrete input—output system and is collectively controllable on V

relative to

some mapping G

The proof is a slight modification of that of Theorem 9.6.10 and is left to the

reader.

9.7. Limit Systems

We say that

is a category if

consists of a class of objects, denoted by obj

pairwise disjoint sets of morphisms, denoted by Hom

(A, B

), for every ordered pair

of objects (

A, B

), and a composition Hom

(

A, B

)

Hom (

B, C

)

→

Hom

(

A, C

denoted by (ƒ, g) → gf, satisfying the following axioms:

(i) For each object A there exists an identity morphism I

∈ Hom

(

A,A

) such

that ƒ I

= ƒ, for all ƒ

∈

Hom

(A, B

) and

for all

∈

Hom

(

C,A

(ii) Associativity of composition holds whenever possible; that is, if

∈

Hom

(A,B

∈

Hom (

B,C

) and h ∈ Hom

(

C,D

), then

(

) = (

)ƒ

(9.217)

246

Chapter 9

Figure 9.3. Universal mapping property of limit systems.

We give some examples of categories.

Suppose

is the category consisting of all general systems and all S-

continuous mappings between systems. Thus, for any two systems S

and S

the

set Hom

equals the set of all

-continuous mappings from

into

Suppose is the category consisting of all general systems and all

homomorphisms between systems. Thus, for two arbitrary systems

and S

the

set Hom of morphisms equals the set of all homomorphisms from S

into

Let

be an

-type hierarchy of systems in

(respectively, in

i.e., each linkage mapping l

is an S

-continuous mapping (respectively, a homo-

morphism). The inverse limit of this hierarchy, denoted by lim or

lim

←C

(respectively, lim or lim

, is a system and a family of

S-continuous mappings

(respectively, homomorphisms

with

whenever i ≤

satisfying the univer-

sal mapping property, contained in Fig. 9.3 (respectively, the universal mapping

property, contained in Fig. 9.4) satisfying: For every system X and S

-continuous

mappings (respectively, homomorphisms) making the corresponding

diagram commute whenever i

≤ j, there exists a unique S-continuous mapping

(respectively, a homomorphism making the

diagram commute.

Figure 9.4. Universal mapping property of limit systems.

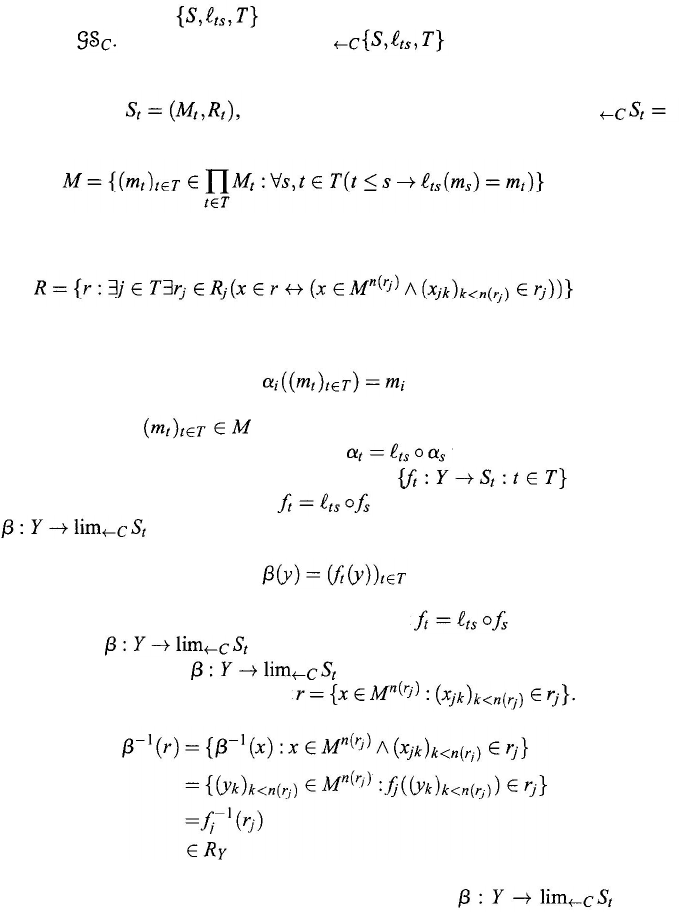
General Systems: A Multirelation Approach

247

From the definition of inverse limits, it can be seen that if a linked hierarchy

of systems has an inverse limit, the limit is unique up to a similarity.

Theorem 9.7.1. Let be a linked

α-type hierarchy of systems in the

category

Then the inverse limit lim

exists.

Proof: Let for each t ∈ T. Define a desired system lim

(

M,R

) as follows:

(9.218)

and

and define mappings

lim

←C

→

by letting

(9.219)

(9.220)

for every object and any i

∈ T. Then it can be checked that the

mappings

are S-continuous and satisfy whenever t ≤ s.

We now let Y =

(

) be a system and a family of

S-continuous mappings such that whenever t

≤ s. Define a mapping

by letting

(9.221)

for each y

∈ M

. Then from the hypothesis that whenever t ≤ s, it

follows that

is well defined.

We now show that is S-continuous. For any relation r ∈ R

there exist

∈ T and r

∈

such that

Therefore,

From the definition of S-continuity it follows that is S

continuous. The uniqueness of β follows from the commutative diagram in the

theorem or Fig. 9.3.



248

Chapter 9

Corollary 9.7.1. Suppose that

is a linked

α-type hierarchy of systems

such that each linkage mapping l

is S-continuous. Then lim

←

is a partial

system of

The proof follows from the proofs of Theorems 9.7.1 and 9.3.10.

Theorem 9.7.2. Let be a linked α-type hierarchy of systems in the

category Then the inverse limit lim

exists.

Proof: We define a system lim

←

= (M,R

) as follows:

(9.222)

and

(9.223)

and for any

define n = n(

), for t ∈ T,and

(9.224)

and

(9.225)

Let

: M → M

, for each t ∈ T, be the projection; i.e.,

Then,

for any relation r ∈ R, there exists

such that r is defined by

Eq. (9.224). Thus, for each t

∈ T. That implies that

each

is a homomorphism from (M,R) into S

We now show that the system (

M,R

) is the inverse limit of the linked hierarchy

Only two things need to be proven: (i) For any system

and

any set of homomorphisms such that

(9.226)

whenever t

≤ s, there exists a homomorphism

so that

(9.227)

for each t

∈ T. To prove (i), define Then β is

a homomorphism from

into

Since for any relation

, then

General Systems: A Multirelation Approach

Since

for all , we have

for each t ∈ T, as mappings between sets. On the other hand, for any relation

and any

This implies that

as mappings from the relation set

into the relation

set R

for each t ∈ T. Hence, for each t ∈ T, as homomorphisms from

(ii) The homomorphism

β is unique. Suppose is another homo-

morphism satisfying for each t

∈ T. Let Then

for all t

∈ T. Thus, for all

This implies that

β' = β on the set , so β' and β induce the same

homomorphism. Hence,

' = β as homomorphisms.



Theorem 9.7.3. Each mapping {g,f

} of a linked hierarchy H = of

systems into a linked hierarchy H' =

of systems induces a mapping

from lim

←

H into lim

←

H', where lim

←

indicates either lim

←

lim

←

Proof: For an object x = (x

)

∈

in lim

←

H and every s' ∈ T', define

(9.228)

The element thus obtained is an object in lim

←

H'. Indeed, for any

s', t'

∈ T' satisfying t' ≤ s', then

For the object x in lim

←

H define ƒ(

) = y in lim

←

H'.

Then

is a mapping from

lim

←

H into lim

←

H'.

The mapping ƒ : lim

←

H → lim

←

H' in the proof of Theorem 9.7.3 is called

the limit mapping induced by {g,

} and is denoted by ƒ = lim

←

{

Theorem 9.7.4. Let

{

,ƒ

}

be a mapping of a linked hierarchy of systems H =

to a linked hierarchy of systems H' = If all mappings ƒ

are one-to-one, the limit mapping

ƒ = lim

←

{g,ƒ

}

is also one-to-one. If, moreover,

all mappings

are onto, ƒ is also an onto mapping.

249

systems into systems.



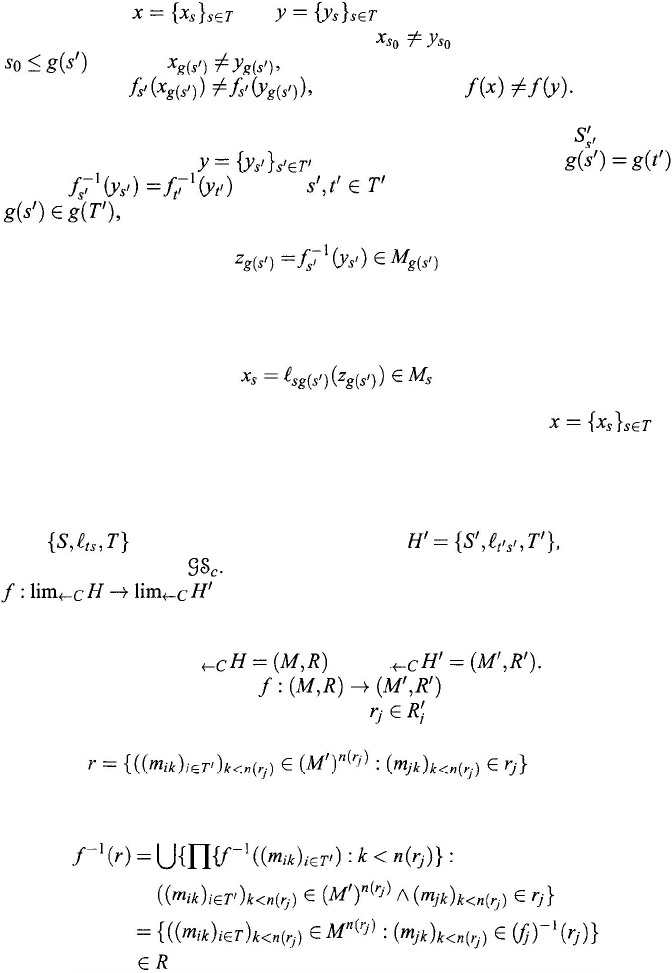
Proof: Let

and

be two distinct objects of the limit

system lim

←

Take an s

∈ T such that and an s' ∈ T' satisfying

Clearly,

so it follows from the hypothesis that ƒ

is one-

to-one, that is,

which shows that

Therefore,

the limit mapping ƒ is one-to-one.

We now suppose that ƒ

is a one-to-one mapping from S

g (s')

onto

for every

∈ T'. Take an object

from lim

←

H'. It follows that

implies

for any satisfying s' ≥ t', so that for any

the element

(9.229)

is well defined. For any s

∈ T choose an element s' ∈ T' such that s ≤ g

(

) and

define

(9.230)

It can be verified that x

does not depend on the choice of s', that is

an element in lim

←

H, and that ƒ

(

) =

That shows ƒ is an onto mapping.



Theorem 9.7.5. Suppose that {

,ƒ

}

is a mapping of a linked hierarchy of systems

H = into a linked hierarchy of systems where H and

H' are in the category

If all mappings

are S-continuous, the limit mapping

is also S-continuous.

Proof:

Suppose lim and lim

Theorem 9.7.3

implies that the limit mapping is well defined. Let r be a

relation in lim

←

H'. There exist j ∈ T' and

such that

(9.231)

Then

Thus, from the definition of S-continuity, the limit mapping ƒ is S

-continuous.



250

Chapter 9

General Systems: A Multirelation Approach

251

Theorem 9.7.6. Suppose that H = {

S, l

, T

} and H' = {S', l

t's'

, T'} are two

linked hierarchies of systems in the category and {

g,ƒ

} is a mapping

from H into H'. If all mappings ƒ

are similarity mappings, the limit mapping

f : lim is also a similarity mapping.

Proof:

Applying Theorem 9.7.4, we know that the limit mapping f is a

bijection from lim

←

H onto lim

←

H'. Theorems 9.2.4 and 9.7.5 imply that f is

also S

-continuous. Now, in order to show that

–1

is S-continuous from lim

←

onto lim

←

H, it suffices to show that f is a homomorphism from lim

←

H into

lim

←

H'.

Let r

∈ R be a relation such that there exist j ∈ T and r

∈

satisfying

Then

(9.232)

Therefore, the limit mapping f is a similarity mapping from lim

←

H onto

lim

←

H'.

Theorem 9.7.7. Suppose that H = {

S, l

, T

} and H' = {S', l

t's'

, T'

} are two

linked hierarchies of systems in the category and that {

g,ƒ

} is a map-

ping from H into H'. If all mappings ƒ

are homomorphisms, the limit mapping

f : lim

←

H → lim

←

H' is also a homomorphism.

Proof: It suffices to show that for any relation r in the system lim

←h

H =

(

M, R

), ƒ(

) is a relation in the system lim

←

H' = (M', R'

To this end, let

where R

is defined by Eq. (9.223), such that

(9.233)

Then

Hence, f (r

)

∈

R'.

(9.234)

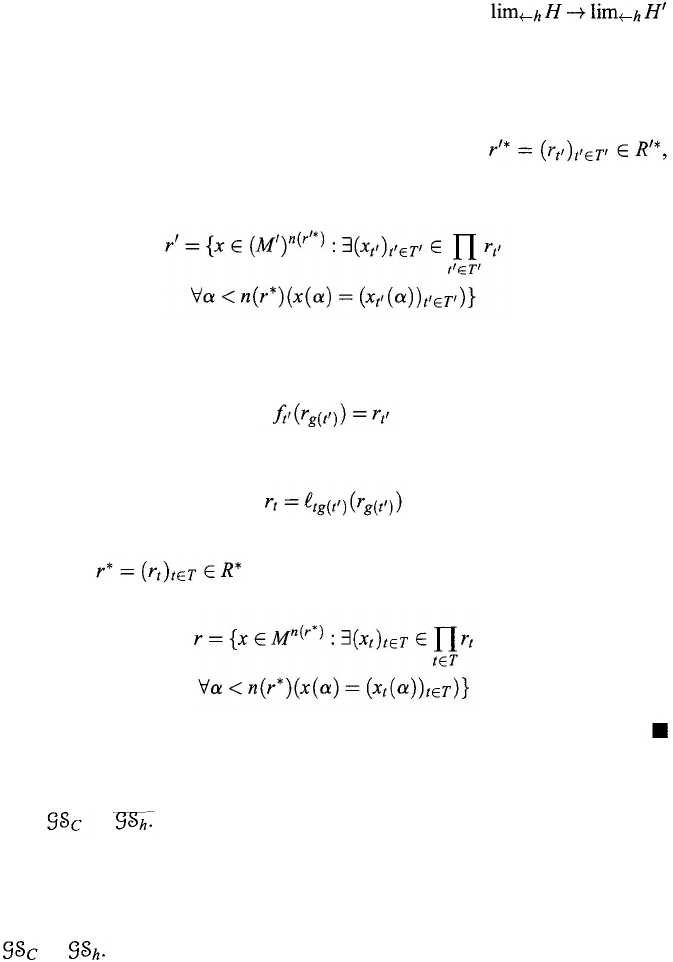
252

Chapter 9

Theorem 9.7.8. Under the same hypotheses as in Theorem 9.7.7, if all mappings

, in addition, are similarity mappings, the limit mapping f

is also a similarity mapping.

Proof:

By Theorems 9.7.4 and 9.7.7, it suffices to show that for any relation

r' in the system lim

←h

H’ = (M',R'), there exists a relation r in the system

lim

←

H = ( M,R ) such that f

(

r ) = r'. Pick an element

where R'

is defined by Eq. (9.223) with R

, T, and l

replaced by R'

, T', and

t's'

, respectively, such that

(9.235)

From the hypothesis that each f

is a similarity mapping from S

(

)

onto S'

, it

follows that there exists exactly one relation r

(t'

)

∈

g(t'

)

such that

(9.236)

Now for any t

∈ T choose a t' ∈ T' such that g

(

) ≥ t. Define a relation r

∈

(9.237)

It can be shown that the definition of r

does not depend on the choice of t'. Then

an element

is well defined, where R

is defined by Eq. (9.223).

The relation r

∈ R, defined by

(9.238)

satisfies f(r ) = r

Corollary 9.7.2. Let {S, l

,T} be a linked α-type hierarchy of systems in cate-

gory

T' a cofinal subset of T. Then lim

←

{S, l

} is similar to

lim

←

{S, l

}, where lim

←

indicates either lim

←

lim

←

The result follows from Theorems 9.7.6 and 9.7.8.

Corollary 9.7.3.

Let

{

S, l

, T

}

be a linked

-type hierarchy of systems in category

If the partially ordered set T has a maximum element t

∈ T, then

the systems lim

←

{

S, l

, T

}, lim

←

{S, l

, T

and S

are similar.

The result follows from Corollary 9.7.2.

General Systems: A Multirelation Approach

253

Corollary 9.7.4. Suppose that {S, l

, T

} is a linked α-type hierarchy of systems

in the category Then the limit system lim

←

is a partial system of ∏{ S

∈ T

The result follows from the proofs of Theorems 9.7.2 and 9.3.9.

Theorem 9.7.9. Let {

S, l

, T

} be a linked α-type hierarchy of systems in the

category such that one of the states S

is connected. Then the inverse limit

system lim

←

{

S, l

, T

} is connected.

The result follows from Theorems 9.7.1 and 9.4.3.

Let {S, l

} be a linked α-type hierarchy of systems such that for every

element in the thread set

, there exists a set

T, s

≥ t} of linkage mappings, where each m

is again a system. The 1-level

inverse limit, denoted by or when all relevant linkage

mappings are S-continuous, or or when all relevant

linkage mappings are homomorphisms, is defined by lim

←

= (M,R), where

lim

←

indicates

and the object set M and the relation set R are

defined as follows: There exists a bijection h :

→ M such that

(9.239)

and

R = {

(

) : r is a relation in lim

}

←

where lim

←

indicates either lim

←

or lim

←

Theorem 9.7.10. Let {S,l

, T } be a linked α-type hierarchy of centralizable

systems in the category If the 1-level inverse limit system

exists, then the system

is centralizable.

Proof: The proof follows from the fact that if C

is a center of the system S

for each t ∈ T, then the inverse limit lim

←c

is a center of the 1-level inverse

limit

Theorem 9.7.11. Let {S, l

, T

} be a linked α-type hierarchy of centralizable

systems in the category If the 1-level inverse limit system

exists, then the limit system is also centralizable.

Proof: This theorem follows from the fact that if C

is a center of the system

, for each t ∈ T, then the inverse limit lim

←

is a center of the 1-level inverse

limit