Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

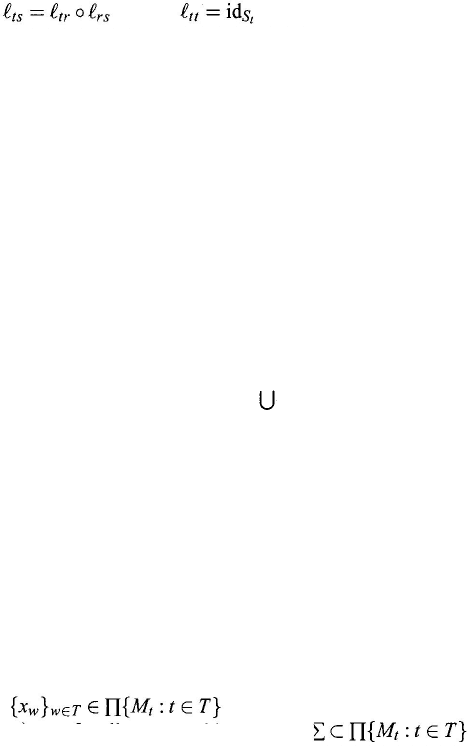
224

Chapter 9

9.5. Hierarchies of Systems

Let (T, ≤) be a partially ordered set with order type α. An α-type hierarchy

S of systems over the partially ordered set (T,

≤) is a function defined on T such

that for each t

∈ T,S(

) = S

= (

, R

) is a system, called the state of the α-type

hierarchy S at the moment t. Without causing confusion, we omit the words “over

the partially ordered set (

T, ≤) .”

For an

-type hierarchy S of systems, let

→ S

be a mapping from the

system S

into the system S

for any r, t ∈ T, with r ≥ t such that

and

(9.124)

where r, s, t are arbitrary elements in T satisfying s ≥ r ≤ t, and id

the identity mapping on the set M

. The family { l

: t, s ∈ T, s ≥ t} is a family

of linkage mappings of the

α-type hierarchy S, and each mapping l

a linkage

mapping from

into S

-type hierarchy of systems S, denoted {

S, l

} or

{S(

}, is

referred to as a linked

-type hierarchy (of systems) if a family {

t, s

∈ T, s ≥ t}

of linkage mappings is given.

Theorem 9.5.1 [ZFC]. Let S be a nontrivial

α-type hierarchy of systems; i.e.,

each state S

is a nontrivial system. Then there exists a family {

: t,s ≤ T, s ≥ t}

of linkage mappings of S.

Proof: Suppose S ), for each t

∈ T. From the Axiom of Choice

it follows that there exists a choice function C : T

→

(

, R

{

: t ∈ T} such that

(

) ∈ M

for each t ∈ T. A family { l

: t ,s ∈ T, s ≥ t

} of linkage mappings of

S can now be defined. For any s, t ∈ T with s > t, let

(

) = C

(

)

(9.125)

for all x ∈ M

and



Question 9.5.1. How many families of linkage mappings are there for a given

α-type hierarchy of systems?

Suppose {

S, l

, T

} is a linked

-type hierarchy of systems, where

= (

, R

)

for all t

∈ T. An element is called a thread of the linked

-type hierarchy

(

) = x

for all s, t ∈ T with s ≥ t. Let

be the subset of all threads, which will be called the thread set of the hierarchy

{

S, l

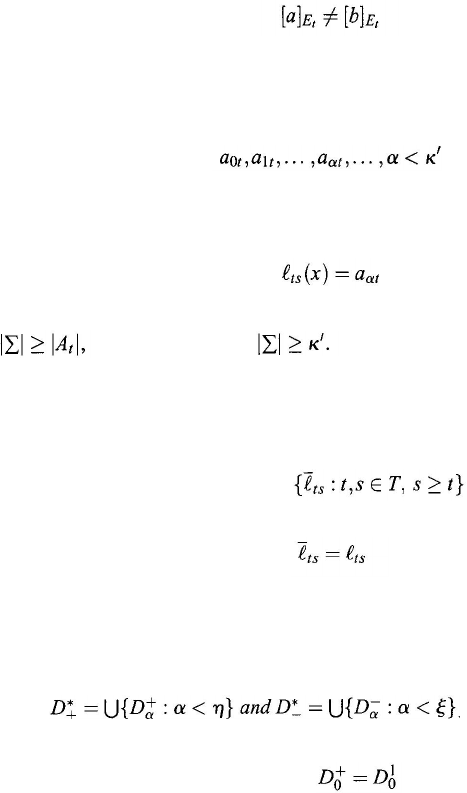
General Systems: A Multirelation Approach

225

Theorem 9.5.2 [ZFC]. Let κ be a cardinal number and S an α

-type hierarchy of

systems such that

⏐

⏐ ≥ κ for each t ∈ T. Then for any nonzero cardinal number

κ ' ≤ κ, there exists a family

{ l

: t, s ∈ T, s ≥ t} of linkage mappings of S such

that

⏐∑⏐ ≥

Proof:

From the hypothesis that for any

∈

⏐

⏐ ≥ κ', and the Axiom of

Choice, it follows that, for any

∈

there exist

⊂ M

satisfying

⏐

⏐ = κ ', and

an equivalence relation

on the object set M

such that M

= { [a]

: a ∈ A

}

and that for any distinct a, b ∈ A

(9.126)

Again, from the Axiom of Choice it follows that there exists a set of well-order

relations

{≤

: t ∈ T} such that, for each t ∈ T, the relation ≤

well-orders A

follows:

(9.127)

For any

s, t

∈

with

we now define a mapping

: S

→ S

. For any

∈

there exists exactly one α < κ such that x ∈ [

]

. Then define

(9.128)



Then {

: t, s ∈ T, s ≥ t} is a family of linkage mappings, where l

= id

, and

for any t

∈ T. Thus

Question 9.5.2. Suppose that S is an

α-type hierarchy of systems over a partially

ordered set (

T, ≤) and { l

s, t

∈

, s ≥ t

} is a family of linkage mappings of the

hierarchy of systems {

: t ∈ T

}, where T

is a proper subset of T. Under what

conditions does there exist a family

of linkage mappings for

S such that

(9.129)

for all s, t

∈ T

with s ≥ t?

Lemma 9.5.1 [ZFC]. Let D

⊂ T be a cofinal and coinitial subset in a partially

ordered set (T,

≤

Then there exists a subset T

= D

∪

of D such that

(a) for some ordinals

η and

ξ such that

(9.130)

226

Chapter 9

(b) Let

then D

is a maximal

antichain in D – E

for any β < η.

(c)

Let

Then D

–

is a maximal

antichain in D – E

–

for each β < ξ.

(d)

is cofinal and coinitial in T.

Proof: First, note the construction of D

. From the Axiom of Choice it

follows that there exists an order relation

≤

on T which well-orders T as

(9.131)

where ≤ and ≤

are generally different. Let d

be the <

-initial element of D,

and

⊂ D such that

and d

and d are incomparable under ≤

}

(9.132)

otherwise, let

be the initial element of (D

, <

Suppose that sequences {

: α < η} and {

: 0 ≠ α < η

} have been defined,

for some ordinal η > 1, such that

(i)

{

: α < η

} is an antichain under the order <.

(ii) for all

α, β < η with α > β.

(iii)

For each α < η, d

is the initial element of the well-ordered set (D

, ≤

(iv) For each

α < η, d

d, for all d ∈ D

, and d

is incomparable with d

under the relation <, for each d

∈ D

, for each β with α < β < η.

If η is a limit ordinal, let

(9.133)

. Then D

is a maximal antichain in D under ≤.

be the initial element of (D

, <

). By (iv) {d

: α < η + 1} is

an antichain under the relation

≤; and for each α < η, d

d for each d ∈ D

and d are incomparable under ≤ for each d ∈ D

η = ξ + 1 is isolated, let be defined by

and d are incomparable under

≤

}

(9.134)

If then

is a maximal antichain in D under the

order

≤

. If

let

be the initial element of (

≤

). Then [

+ 1}

is an antichain in D under ≤

, and

for all β < η. For each α < η + 1,

General Systems: A Multirelation Approach

227

d, for all d ∈ D

, and d

is incomparable with

∈

under ≤ for any β,

with α < β < η

+ 1.

By transfinite induction, sequences {d

: α < η } and with

properties (i)–(iv) can be defined, such that if a subset with

property (iv) can be defined in the way discussed earlier, it must be that D

Let

Then D

is a maximal antichain in (

, ≤). Using

transfinite induction to consider sets

such that x > d} and

and applying the same technique we used before,

we can show that ordinals

and

and subsets

and 0 ≠ β < ξ, exist such that properties (a)–(d) in the lemma hold.



Theorem 9.5.3 [ZFC]. Suppose that S is an α-type hierarchy of systems over a

partially ordered set (T,

≤) such that there exists a cofinal and coinitial subset

⊂ T such that is a family of linkage mappings for the

hierarchy of systems

{

: t ∈ D

}

satisfying

(9.135)

for any s,r,t

∈ D with s ≥ r > t. Then there exists a subset T

⊂ D such that

(i) T

is cofinal and coinitial in T.

(ii) There is a family

of linkage mappings for S.

(iii) For any s, t

∈ T

with

Proof:

Let

⊂ D be the subset defined in the proof of Lemma 9.5.1. Let us

rewrite T

∪

where,

(9.136)

and

(9.137)

and pick one t ∈ T. There are two possibilities: (1) t ∈ T

and (2) t ∈ T

Case 1: t ∈ T

. There then exists an ordinal α < ξ such that there exists

and assume that

α is the initial one in ξ with this property.

Now we assume that e

< t.

α = δ + 1 is isolated, there exists

such that

From the

Axiom of Choice it follows that for any s

∈ T satisfying there exist

an A

⊂

such that

an equivalence relation

on M

such that

and satisfies, for any distinct

a, b

∈

(9.138)

228

Chapter 9

and a set of well-order relations such that, for any s ∈ T

satisfying e

< s < e

, the relation <

well-orders

as follows:

(9.139)

where

follows:

for all i < ⏐A

⏐, and the relation <

well-orders

(9.140)

We now define mappings

for all s, t ∈ T, with e

≤ s < t < e

as follows: For any x ∈ M

there exists exactly one a

∈

such that

If s > e

, let

(9.141)

If s = e

, let

(9.142)

Define mappings

for all s

∈ T with e

< s < e

as follows:

(9.143)

If α is a limit ordinal, then by definition α > 0. Let

(9.144)

From the Axiom of Choice it follows that for any

∈

, there exists an A

⊂

satisfying

where

∈

–

satisfies t < q. An equivalence relation

on M

exists such that

satisfies, for any distinct

be a set of order relations such

that, for any

∈

, the relation <

well-orders M

as follows:

(9.145)

where

for all i, and the relation <

well-orders

as follows:

(9.146)

We now define mappings

for all

as follows: For

any

∈

there exists exactly one

such that

let

(9.147)

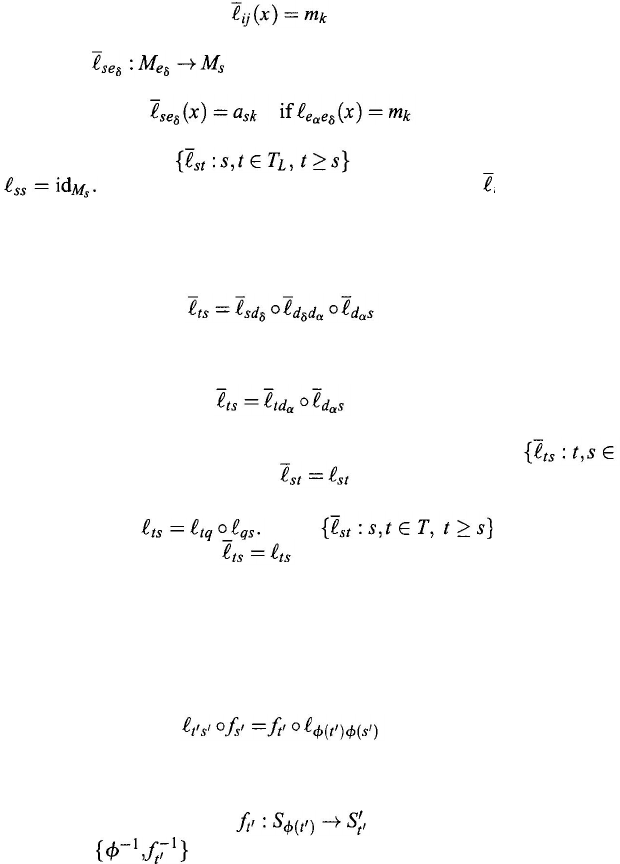
General Systems: A Multirelation Approach

229

If j = e

, let

(9.148)

Define mappings

for all

∈

and all δ < α by

(9.149)

Then it is easy to check that

is a family of linkage mappings,

where

Furthermore, for any s, t ∈ T

with s > t, if

is undefined

above, then there exist

α, β < ξ such that there exist d

∈

–

and d

∈

, with

< t < d

< s. Let α and β be the least ordinals with this property. (1) If

β = δ + 1, then there exists exactly one d

∈

–

such that d

< t ≤ d

. Define

(9.150)

(2) If β is a limit ordinal, define

(9.151)

Case 2: t ∈ T

. A similar method can be used to define a family

T, t

≥

} of linkage mappings such that

for any

s, t

∈

with s ≤ t.

Now let s

∈ T

and

satisfying s > t. There exists exactly one q ∈ D

such

that t

≤ q ≤ s. Define

Then

is a family of

linkage mappings for S such that

for all

s, t

∈

with s ≥ t.



Let H = {S, l

, T} and H' = {S', l

t's'

} be two hierarchies of systems. A

mapping from the hierarchy H into the hierarchy H' is a set {

,ƒ

} of mappings,

where

φ is a nondecreasing mapping from T' into T with φ

(

) cofinal in T, and

for each t'

∈ T' ,ƒ

is a mapping from S

(t'

)

into

such that

(9.152)

i.e., such that the diagram in Fig. 9.2 commutes for any s', t'

∈ T' satisfying s' ≥ t'.

A mapping {

,ƒ

} from H into H' is a similarity mapping if φ is a similarity

mapping from T' onto T and each is a similarity mapping. It is

easy to show that is a similarity mapping from H' into H.

When the partially ordered set (

T, ≤) is a pseudo-tree (i.e., for each t ∈ T the

set {y

∈ T : y ≤ x} is a chain), each hierarchy S of systems over T is called a

treelike hierarchy of systems; each linked hierarchy {

S, l

} of systems is called

a linked treelike hierarchy of systems. A treelike hierarchy B of systems over a

tree T is a partial treelike hierarchy of a treelike hierarchy A of systems over the

same tree T if for each t

∈ T, the state B

is a partial system of the state A

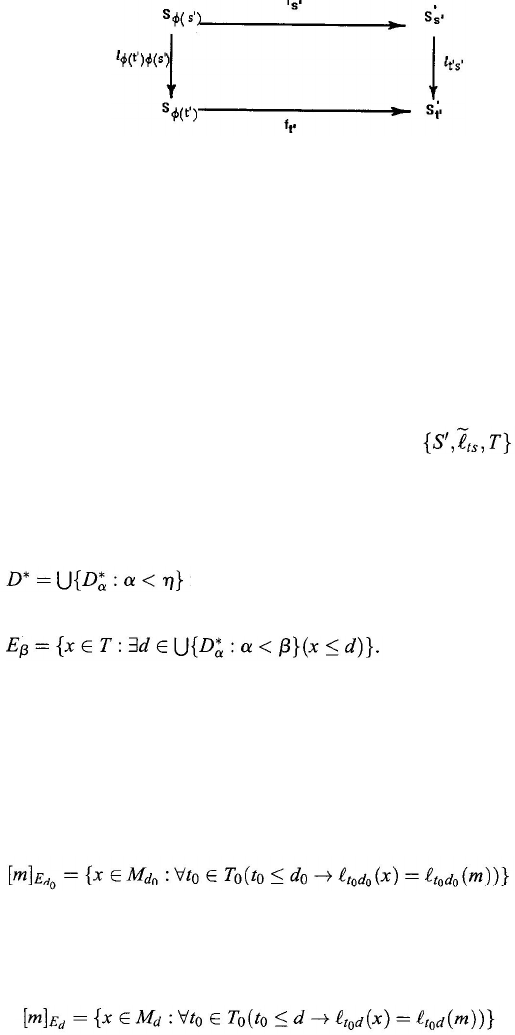
230

Chapter 9

Figure 9.2. A hierarchy mapping guarantees the diagram is commutative.

Theorem 9.5.4 [ZFC]. Let {S,

,T } be a linked treelike hierarchy of systems

such that the partially ordered set (

≤

)

satisfies

(i)

T has a subset T

consisting of all minimal elements in T such that for

each t

∈ T, there exists at

∈

such that t

≤ t.

(ii)

There exists a cofinal subset D ⊂ T such that l

is an onto mapping for all

s,t

∈ D

∪

with s ≥ t.

Then there exists a nontrivialpartial linked hierarchy

{

S, l

, T

}

such that the state S'

(

) is embeddable in the state S'

(

) for all t,s ∈ T with s ≥ t.

Proof:

From Lemma 9.5.1 it follows that there exists

⊂ D such that

(a)

for some ordinal η > 0.

(b) D

is a maximal antichain in D – E

, for each β < η

, where

is cofinal in T.

Let

≤

indicate the order relation on T defined in the proof of Lemma 9.5.1.

From the hypothesis that l

is onto for any s,t ∈ D

∪

with s ≥ t, it follows that

each linkage mapping

is onto, for all

∈

and

∈

satisfying r ≥ t

. Let d

be the initial element of the well-ordered set (D* , ≤ *). We define an equivalence

relation

on M

such that the equivalence class

(9.153)

for each m

∈ M

. By transfinite induction, for each element d in (

, ≤

) an

equivalence relation E

on the object set M

of the state S

can be defined such

that the equivalence class

(9.154)

General Systems: A Multirelation Approach

231

The linkage mapping ltr , for any t

r ∈ D

with r ≥ t, can induce a mapping

from

onto

such that

(9.155)

where [

]

∈ M

satisfies l

) = m

. In fact, for each [m

]

∈

there exists exactly one [

]

∈

such that

(9.156)

Therefore,

and

is well defined.

For any maximal linearly ordered set B ⊂ D

, called a branch, Lemma

9.5.1 implies that (

≤

) is well-ordered. Let b be the initial element in B. For any

fixed element

∈

, from the fact that (B, ≤ ) is well-ordered and AC, it follows

that there exists an element

such that

(9.157)

and that there exists an element such that

(9.158)

for all i,j ∈ B with i ≥ j.

From AC it follows that there exists a subset

such that, for each x

∈ M

(9.159)

where

(

) = g

, for all s,t ∈ B with s ≥ t. Let P

(B) → M

, for each

∈

be the projection, and define

(9.160)

Then

is a hierarchy of systems and a partial linked hierarchy

Let X be the set of all branches in the set D

. By transfinite induction,

hierarchies of systems, for each B

∈ X , can be defined such that

for any branches

∈ X and d ∈ CB,

(9.161)

Here we used the hypothesis that

is a pseudotree. Therefore, for each

∈

we can define

(9.162)

232

Chapter 9

where B is a branch containing d. Then S'

is a partial system of S

and

is a nontrivial linked hierarchy of systems such that the state

S’

(

) = S'

is embeddable in the state S’

(

s) = S’

, for any t,s ∈ D

satisfying

≤ s.

For any t

∈ T – (

), choose

∈

such that s ∈ D

, where α is the

least ordinal in

η with this property, and s > t. We take a partial system S'

of the

system

defined by

(9.163)

Then it is not hard to check that is a nontrivial partial linked

hierarchy of {S

} such that the state S’

(

) is embeddable in the state S’

(

)

for any s,t ∈ T , with s ≥ t.

When the partially ordered set (T,

≤ ) is a total ordering, each hierarchy S of

systems over T is called a time system; each linked hierarchy {

} of systems

is called a linked time system. In this case, T is called the time set (or time axis)

of the time system S.

An ordered triple (T, +,

≤ ) is called an ordered Abelian group if (T, +) is

an Abelian group and (T,

≤ ) is a linearly ordered set such that for any elements

(9.164)

We conclude this section with a discussion of time systems over ordered

Abelian groups. This kind of time system is called a system over a group. If the

time system is also a linked time system, we call the system a linked system over

a group.

Suppose (

T, +, ≤ ) is an ordered Abelian group. We let 0 be the identity in T,

and, for any

∈

⏐

indicates the absolute value of

, defined by

⏐x

⏐

= max{ – x,x }

(9.165)

where –x is the additive inverse of x. For any integer n

if n = 0

if n > 0

if n < 0

(9.166)

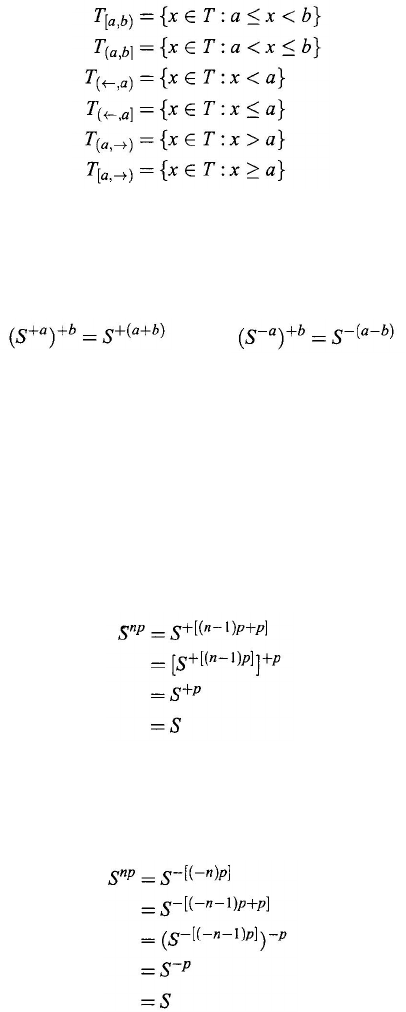
General Systems: A Multirelation Approach

233

The following notation will be used:

Let S be a system over a group and t

∈ T a fixed element. The right transfor-

mation of S, denoted S

–t

, is defined by

–t

(

) = S

(

t – t

) for each

∈

; the left

transformation of S, denoted S

, is defined by

) = S

(

t+t

) for each t ∈ T.

Theorem 9.5.5. Suppose that S is a system over a group. Then for any a,b

∈ T,

and

A system S over a group T is periodic if there exists p

∈ T such that p ≠ 0 and

= S. The element p is called a period of S.

Theorem 9.5.6. Let S be a system over a group T. If S is periodic with p

∈ T

as its period, then for each integer n, S

= S, where S

= S

+np

if n ≥ 0, and

= S

– [(– n)

]

if n < 0.

Proof:

We show the theorem by induction on n.

Case 1

: n ≥ 0. If n = 0, the result is clear. Suppose S

+kp

= S for each integer

k satisfying 0

≤ k < n. Then it follows that

Thus, by induction, we have S

+np

= S for each n ≥ 0.

Case 2

: n < 0. If n =

–1, in the condition that S

(

t + p

) = S

(

t), for each

∈ T, let t = x – p. Then S

(

x) = S

(

x – p ) for each x ∈ T. This says that S

–p

= S.

Suppose S

–kp

= S for each integer k satisfying 0 ≤ k < –n. Then it follows that