Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

194

Chapter 9

and

We then define is not a system} and

By mathematical induction a sequence can be defined. Let

Then Theorem 9.1.3 guarantees that M(S) consists of

all fundamental objects in S; and from the uniqueness of each *M

it follows that

M(S) is uniquely determined by S.

Theorem 9.1.5. Let S = (M,R) be a system such that, for any r

∈ R, the length

n(r ) = 2. Then

(9.1)

where p

(X) is the power set of X and p

)

= p

(X)) for each i = 1,2, . . .

Proof: For each element (x,y

)

∈ r, (

x,y) = {{x},{x,y}}

∈ p

(M ) and r ∈

(M). Therefore, R ∈ p

(M). Since {M} ∈ p (M) and (

M, R

)

(M)), it follows that the inclusion in Eq. (9.1) holds.

Question 9.1.1. Give a structural representation for general systems similar to

that in Theorem 9.1.5.

A system S = (

M, R

)

is called centralized if each object in S is a system and

there exists a nontrivial system C =(M

) such that for any distinct elements

x,y

∈ M, say x = (

) and y = (

, R

), then

where

The system C is

called a center of the centralized system S.

Theorem 9.1.6 [ZFC]. Let k be any infinite cardinality and

θ > k a regular

cardinality such that, for any Assume that S = (M, R) is a

system satisfying

⏐

⏐ ≥ θ and each object m ∈ M is a system with m = (

)

and

⏐

⏐ < κ. If there exists an object contained in at least θ objects in M, then

there exists a partial system S' =

(

M', R' ) of S such that S' forms a centralized

system and

⏐

⏐ ≥ θ.

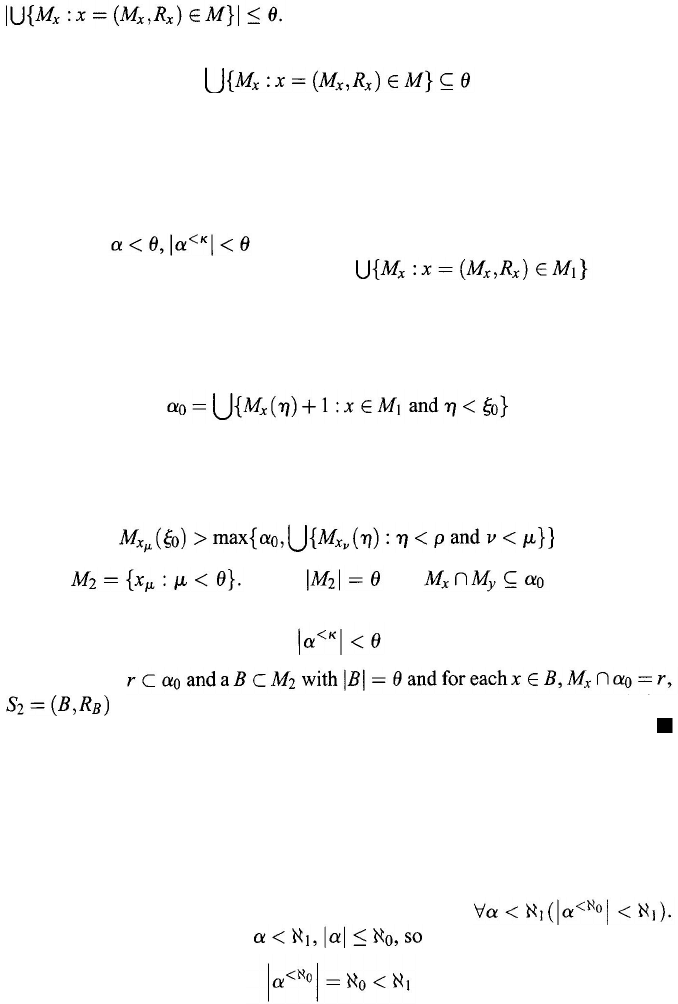
General Systems: A Multirelation Approach

195

Proof:

Without loss of generality, we assume that ⏐

⏐ = θ and that

there is a common element in all the object systems in M.

Then

Since the specific objects in each M

for each

object x = (M

, R

) ∈ M, are irrelevant, we may assume that

Then, for each x =(

) ∈ M, the object set M

has some order type < κ

as a subset of θ. Since θ is regular and θ > k, there exists a ρ < k such that

= {x ∈ M : M

has order type ρ} has cardinality θ. We now fix such a ρ and

deal only with the partial system S

= (M

) of

where

is the restriction of

the relation set R on M

For each

implies that less than θ objects of the partial system

have object sets as subsets of α. Thus, is cofinal

θ. If x ∈ M

and ξ < ρ, let M

(ξ) be the ξth element of M

. Since θ is regular,

there is some

ξ such that {

(ξ) : x ∈ M

} is cofinal in θ. Now fix ξ

to be

the least such

ξ. Then the condition that there exists a common element in each

system in M

implies that we can guarantee that ξ

> 0. Let

Then

< θ and M

( η) < α

for all x ∈ M

and all η < ξ

By transfinite induction on

µ < θ, pick x

∈ M

so that M

(ξ

) > α

and

(ξ

) is above all elements of earlier x

; i.e.,

Let

Then

and

whenever x =

(

) and y = (

) are distinct objects in M

. Since for each α < θ,

there exists an

forms a centralized system, where

is the restriction of the relation

set R on B.

Corollary 9.1.1. If S is a system with uncountable (or nondenumerable) object

set, if each object in S is a system with a finite object set, and if there exists an

object contained in at least

ℵ

objects in S, there exists a partial system S* of S

with an uncountable object set and S* forms a centralized system.

Proof: It suffices from Theorem 9.1.6 to show that

This is clear because for each

(9.2)

196

Chapter 9

A system S = (M,R) is strongly centralized if each object in S is a system and

there is a nondiscrete system C = ( M

) such that for any distinct elements

x and y

∈ M, say x = (

) and

and

The system C is called an S-center of S.

Question 9.1.2. Give conditions under which a given system has a partial system

which is strongly centralized and has an object set of the same cardinality as that

of the given system.

9.1.1.

A Brief Historical Remark

Roughly speaking, the idea of systems appeared as long ago as Aristotle. For

example, Aristotle’s statement “the whole is greater than the sum of its parts”

could be the first definition of a basic systems problem. Later, many great thinkers

used the languages of their times to study certain systems problems. Nicholas of

Cusa, for example, a profound thinker of the fifteenth century, linking medieval

mysticism with the first beginnings of modern science, introduced the notion of

the coincidentia oppositorum. Leibniz’s hierarchy of monads looks quite like that

of modem systems. Gustav Fechner, known as the author of the psychophysical

law, elaborated in the way of the native philosophers of the nineteenth century

supraindividual organizations of higher order than the usual objects of observation,

thus romantically anticipating the ecosystems of modem parlance; for details, see

(von Bertalanffy, 1972).

The concept of systems was not introduced formally until the 1920s. Von

Bertalanffy began to study the concept of systems formally in biology. Since then,

more and more scholars have studied the concept of systems and related topics.

For example, Tarski (1954–1955) defined the concept of relational systems. Hall

and Fagan (1956) described a system as a set of objects and some relations between

the objects and their attributes. They did not define mathematical meanings for

objects nor for attributes of the objects. In 1964 Mesarovic began to study the

model of general systems in the language of set theory. His final model (Mesarovic

and Takahara, 1975) reads: A system S is a relation on nonempty sets:

(9.3)

After considering the interrelationship between the systems under concern and

some environments of systems, Bunge (1979) gave a model of systems as follows:

Let T be a nonempty set. Then the ordered triple W = (C,E,

) is a system over T

if and only if C and E are mutually disjoint subsets of T and S is a nonempty set of

relations on

∪

; the sets

and

are called the composition and an environment

of the system W, respectively. Klir (1985) introduced a philosophical concept of

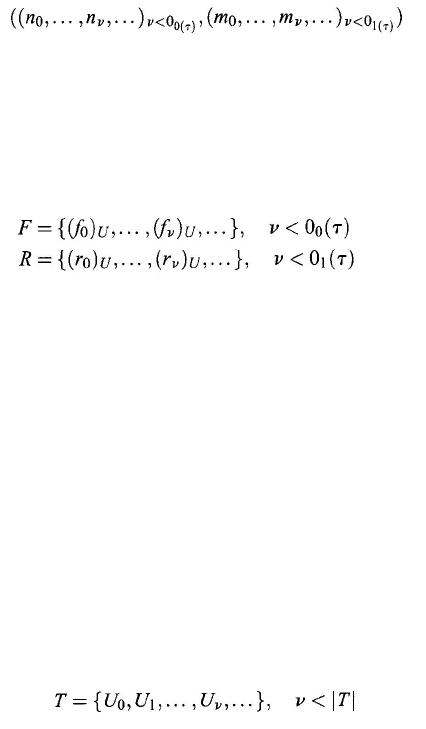
General Systems: A Multirelation Approach

197

general systems. The concept of general systems discussed intensively in this

chapter was first introduced by Lin and Ma (1987; 1987).

We conclude this section with three mathematical structures related to the

concept of general systems: structure, L-fuzzy system, and G

-system.

9.1.2. Structures

Let A be a set and n a nonnegative integer. An n-ary operation on A is a

mapping f from A

into A. An n-ary relation r on the set A is a subset of A

. A

type τ of structures is an ordered pair

(9.4)

where 0

(

τ)

and 0

(

)

are fixed ordinals and n

and m

are nonnegative integers.

For every

(

)

there exists a symbol

of an n

-ary operation, and for every

(

)

there exists a symbol

, of an m

-ary relation.

A structure U (Gratzer, 1978) is a triplet (A, F, R), where A is a nonempty set.

For every

(

)

we realize f

v as an n

-ary operation (

)

on A, for every

(

)

we realize r

as an m

-ary relation (

)

on A, and

(9.5)

(9.6)

If 0

(

) = 0, U is called an algebra and if 0

(

) = 0, U is called a relational

system.

It can be seen that the concept of algebras is a generalization of the concepts

of rings, groups, and the like. Any n

-ary operation is an (n + 1)-ary relation.

Therefore, the concept of relational systems generalizes the idea of algebras, and

the concept of structures combines those of algebras and relational systems. The

fact that any topological space is a relational system shows that the research of

relational systems will lead to the discovery of properties that topologies and

algebras have in common.

Example 9.1.1. We show that any topological space is a relational system, thus

a general system. Let (X, T) be a topological space [for details see (Engelking,

1975)]. Then for each open set

∈

, there exists an ordinal number

(

U) = 1

such that U

∈ X

. Therefore, (

X, T

) is also a system with object set

, and relation

set T

, and the length of each relation in

is 1. Now, applying the Axiom of Choice

implies that the topology T can be well-ordered as

(9.7)

where each open set is a 1-ary relation on X. So (X , Ø, T) becomes a structure,

which is a relational system.

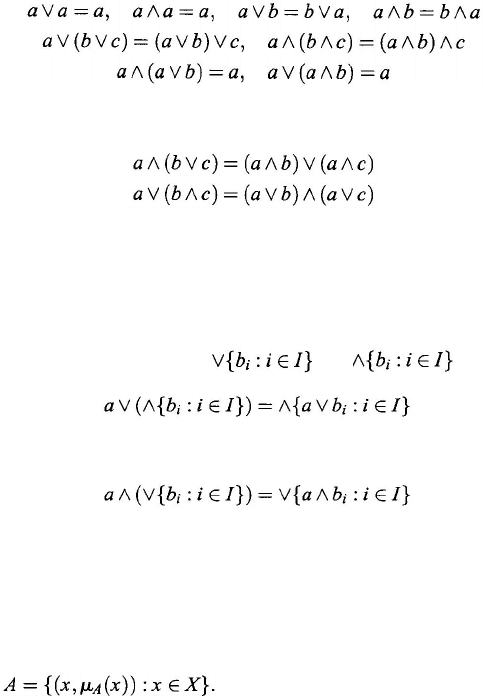
198

Chapter 9

and

A systematic introduction to the study of structures can be found in (Gratzer,

1978). Many great mathematicians worked in the field, including Whitehead,

Birkhoff, Chang, Henkin, Jonsson, Keisler, Tarski, etc.

9.1.3. L-Fuzzy Systems

The concept of fuzzy systems (Lin, 1990a) is based on the concept of fuzzy

sets introduced in 1965 by Zadeh. An ordered set (L

≤) is called a lattice if

for any elements

, b ∈ L, there exists exactly one greatest lower bound of a and

, denoted by a ∧ b, and there exists exactly one least upper bound of a and b,

denoted by

∨

, such that

We call a lattice distributive if the lattice, in addition, satisfies

We call a lattice complete if for any nonempty subset A

⊆ L, there exists exactly

one least upper bound of the elements in A, denoted by

∨A or supA, and there

exists exactly one greatest lower bound of the elements in A, denoted by

∧A or

inf

We call a lattice completely distributive if for any a ∈ L and any subset {

∈ I} ⊆ L

, where

is an index set,

and

exist and satisfy

(9.8)

(9.9)

We say that

is a lattice with order-reversing involution if there exists an operator

' defined on L such that for any a, b ∈ L, if a ≤ b

, then

≥

In the following, a completely distributive lattice L with order-reversing invo-

lution is fixed; assume that 0 and 1 are the minimum and maximum elements in

Let X be a set. A is an L-fuzzy set on X iff there exists a mapping µ

∈ L

such that

Without confusion, we consider that A is the

mapping µ

in L

. If µ

, or say A, has at most two values, 0 and 1, then the

L-fuzzy set A can be seen as a subset of X.

General Systems: A Multirelation Approach

199

Suppose that A and B are two L-fuzzy sets on X

. Then

iff

) =

(

x) for all x ∈ X . A ⊂ B iff

for all x

∈ X. If Y ⊂ X, then

Let {A

: i ∈ I

} be a set of

-fuzzy sets on

. Then

and

are defined by

(9.10)

(9.11)

and

for all x ∈ X

S is an L -fuzzy system iff S is an ordered pair (

) of sets, where R is a

set of some L-fuzzy relations defined on the set M; i.e., for any L

-fuzzy relation

r ∈ R

, there exists an ordinal number

(

) such that r is an L-fuzzy set on the

Cartesian product

. The ordinal n is called the length of the L

-fuzzy relation

Theorem 9.1.7.

Suppose that an L-fuzzy system S =

(

M , R ) is such that, for any

∈ R, n

(

) = 2. Then

(9.12)

Proof: S = (M, R) = {{M}, {

, R}} ⊆ p

(

M ∪ R), and for any (x, y, i

)

∈

⊆

M ² × L

and Thus, the inclusion in Eq. (9.12)

holds.

Suppose that

= (

), i = 1, 2, are L

-fuzzy systems. The

-fuzzy system

is a subsystem of the

-fuzzy system

if M

⊆

and for any

-fuzzy relation

∈

, there exists an

-fuzzy relation

∈ R

such that

Example 9.1.2. An example is constructed to show that the equation S

= S

will

not follow from the condition that the L-fuzzy systems

and S

are subsystems

of each other.

Suppose that the completely distributive lattice with order-reversing involution

lattice L is the closed interval with the usual order relation. Let

= {1, 2, …} be

200

Chapter 9

for each

for all

the set of all natural numbers, and

a sequence defined by

= 1 – 1

We now define two

-fuzzy systems,

and

as follows:

and

where

(9.13)

(9.14)

and for any

and

(9.15)

Then it is easy to show that

and

are subsystems of each other, but

≠ S

9.1.4. G-Systems

In this part any set

will be seen as a partially ordered set (

A , ≤

), where the

ordering is defined by

≤

= {(x, x) : x ∈ A

S is a G

-system (Lin and Ma, 1989) of type

where I is an index

set and, for each i

∈ I, K

is a set partially ordered by

≤

iff

is an ordered pair of

sets such that for any

The set K

is called the type of

the relation

, and the set K is called the type of the system S.

The concept of

-systems can be used to study more applied problems because

it contains a more general meaning of relations. The interested reader is encouraged

to consult (Lin and Ma, 1989).

9.2. Mappings from Systems into Systems

Let S

= (

, R

), = 1, 2, be two systems and h : M

→

a mapping. By

transfinite induction, two classes

i = 1, 2, and a class mapping

can be defined with the following properties:

(9.16)

and for each x =

(9.17)

General Systems: A Multirelation Approach

201

For each relation

is a relation on

with length

(

Without confusion, h will also be used to indicate the class mapping

and

is a

mapping from

into S

denoted h : S

→ S

. When h : M

→ M

is surjective,

injective, or bijective, h : S

→ S

is also called surjective, injective, or bijective,

respectively. Let

be a subsystem of

. Then h⎪

X indicates the restriction of the

mapping on X. Without confusion, we use h for h

⎪X.

The systems S are similar, if there exists a bijection h : S

→ S such that

The mapping h is a similarity mapping from S

onto S . Clearly, the inverse mapping h

–1

is a similarity mapping from S

onto

mapping

→ S

is a homomorphism from

into

The quotient system S

E is defined

where µ : M

→ M

E is the canonical mapping defined by µ

(

) = [

]. Then

E = {µ (

) : r ∈ R

Theorem 9.2.1. Suppose that h : S

→ S

is a homomorphism from S

into S

Then

is a similarity mapping, where

and

for each

Proof:

It is easy to check that

is an equivalence relation on the object set

We next show that

is well defined. Let be

such that [

] = [m

], then m

∈ [

], and so h(

) = h

(

). This implies that

Finally, we show that is a similarity mapping; is a

bijection. In fact, let [

] and

be such that and

Therefore,

)

= h (m

This implies that and so

[

] = [m

], contradiction.

For any relation r ∈ R

, there exists a relation s ∈ R

such that r = µ

(

where µ is the canonical mapping from M

into M

Then

(9.19)

Thus,

For any relation

∈

(

), there exists a relation s ∈ R such that r = h (s

Therefore,

This completes the proof that

is a similarity

mapping from

onto

(

) .



Let S

and A be two systems with no nonsystem kth-level objects for each

where

is a fixed natural number. A mapping

: S

→ A is an n

-level

homomorphism from

into A if the following inductive conditions hold, and the

system

is n

-level homomorphic to

Let E be an equivalence relation on the object set M of a system S = (M, R

(9.18)

202

Chapter 9

(1)

For each object

in S

, there exists a homomorphism

, from the object

system

into the object system h

(

(2)

For each

and each

th-level object S

of S

, there exist level object

systems S

, k = 0,1, . . . ,i

–

1, and homomorphisms

, k = 1,2, . . . , i,

such that

is an object of the object system

–1

and h

is a

homomorphism from

into

k –1

(

) for k = 1,2, . . . , i.

When all homomorphisms in this definition are similarity mappings, the map-

ping

is termed as an n

-level similarity, and the system

is n-level similar to

Proposition 9.2.1. Suppose that A, B, and C are systems.

(a) If A is n-level homomorphic to B and B is m-level homomorphic to C, then

A is min{n, m

}

-level homomorphic to C.

(b) If A is n-level similar to B and B is m-level similar to C, then A is

min{

n, m

}

-level similar to C.

The proof is straightforward and is omitted.

A system

is centralizable if it is 1-level homomorphic to a centralized system

under a homomorphism h : S → S

such that for each object m in S, the object

system

and

(

) are similar. Each center of S

is also called a center of S.

Theorem 9.2.2. Let S = (

M, R

)

be a system such that each object in M is a system.

Then S is centralizable, iff there exists a nontrivial system C

, R

) such that

C is embeddable in each object of S. (C embeddable in an object S

in S means

that C is similar to a partial system of S

, and each similarity mapping here is

called an embedding mapping from C into S

Proof: Necessity. If the system S = (M,R

)

is centralizable, there exists a

centralized system S

= (

, R

) such that S is 1-level homomorphic to S

. Let

C be a center of S

. Then C is embeddable in each object of S.

Sufficiency. Without loss of generality, we can assume that the collection of all

object sets of the objects in S consists of disjoint sets. For each

the system C is embeddable in x, so there exists a one-to-one mapping

such that is a partial system of x. Define a new

system

as follows:

(9.20)

and let

be the bijection defined by

(9.21)

General Systems: A Multirelation Approach

203

Then define

(9.22)

So C is a partial system of x

. Let h

be a mapping defined by letting

(x) = x

for each x ∈ M. Then the system h

(

S) is centralized with the system C as a

center. Therefore, S is a centralizable system.



Example 9.2.1.

An example is constructed to show that the hypothesis in Theorem

9.1.6 that there exists an object belonging to at least θ objects in S is essential for

the result to follow and that not every centralizable system is a centralized system.

Consequently, the concepts of centralized systems and centralizable systems are

different.

Let ω

be the first uncountable ordinal number, and

a collection of

-element

subsets of ω

, for some natural number n > 0, such that

⏐

and for any

x,y

∈ M, x

y =

if x ≠ y.

We now consider a system S with object set M

such that for any x

∈ M

is a system with some element in M as its object set, and for any x ∈ M there

exists exactly one x

∈ M

such that x is the object set of the system x* . It is

clear that S has no partial system which forms a centralized system and that S is a

centralizable system.

Theorem 9.2.3. Let

κ and θ be cardinalities satisfying the conditions in Theorem

9.1.6. Assume that S is a system with an object set of cardinality

≥ θ and each

object in S is a system with an object set of cardinality <

κ . There then exists a

partial system S' of S such that the object set of S' is of cardinality

≥ θ and S'

forms a centralizable system.

The proof follows from Theorems 9.1.6 and 9.2.2.

A mapping h from a system S

= (

, R

) into a system S

= (M

) is

-continuous if for any relation r ∈ R

(9.23)

Proposition 9.2.2.

Suppose that h : S

→ S

is a mapping. Then

(i) If the systems S

, i = 1,2, are topological spaces, h is S-continuous, iff it is

continuous from S

into S

(ii) If the systems S

, i = 1,2, are groups, the S-continuity of h implies that h is

a homomorphism from S

into S

(iii) If the systems S

, i =

1,2, are rings, the S-continuity of h implies that h is a

homomorphism from S

into S