Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

Unreasonable Effectiveness of Mathematics: A New Tour

183

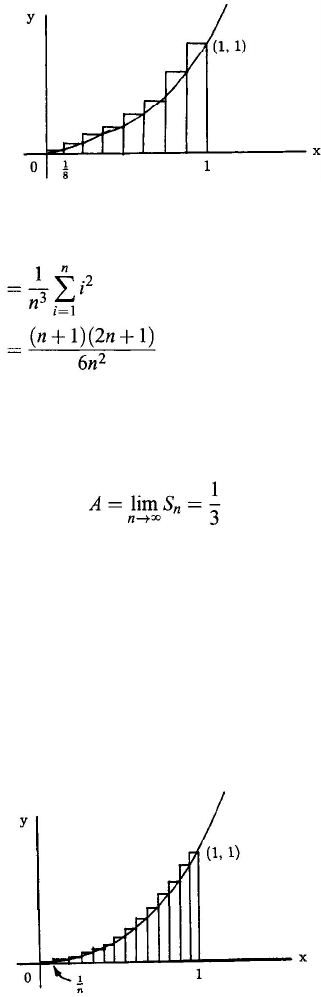
Figure 8.5. Eight-rectangle approximation of the area of the region S.

(8.11)

From Figs. 8.4 to 8.6 it appears that as n increases S

becomes a better and better

approximation to the area of the parabolic segment. In calculus, the area A of the

region S can be found by taking the limit:

(8.12)

Now compare the idea applied in the area problem with that in the vase puzzle

do we have similar recursive procedures? In solving the area problem, we compute

the area S

for n = 1,2,3, . . . ; after all S

’s are computed (based on mathematical

induction we can do this), by taking the limit of the S

’s we get the value for the

area A of S. If Explanation 2 were correct, how could we finish computing the

’s? If we are not able to, we could not take the limit of the S

's, either. Some

readers may get confused here and do not see the similarity because the concept

of limit is involved.

Figure 8.6. n

-rectangle approximation of the area of the region

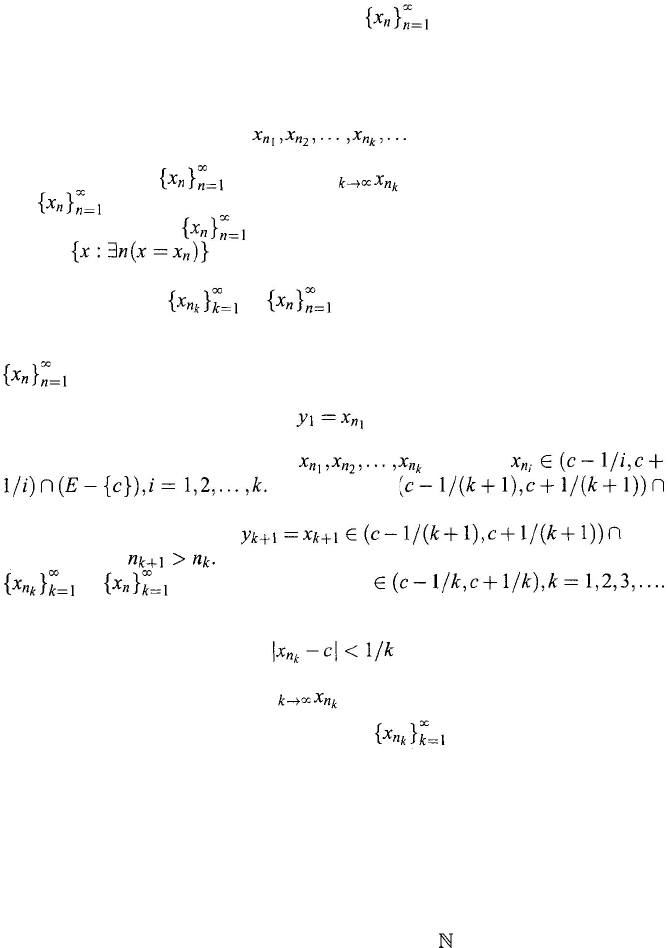
184

Chapter 8

Example 8.6.2 [Department of Mathematics (1978)]. When studying the con-

cept of convergence of a sequence, we have a well-known theorem: Each bounded

sequence of numbers must have a convergent subsequence. Let us look at the

proof of the theorem.

Case 1: Suppose the bounded sequence is made up of a finite set of

numbers. Then one of the numbers, say

, must appear repeatedly infinitely many

times. If the locations that the number

appears are the

st term, n

nd term, . . .,

then

(8.13)

is a subsequence of

satisfying lim

Therefore, we have proved

that has a convergent subsequence.

Case 2: Suppose is made up of infinitely many numbers. Then the

set E = is a bounded infinite set. By a theorem of Weierstrass

(1815–1897), the set has at least one cluster point

We now show that there must

exist a subsequence of which converges to c.

Since

is a cluster point of

, there must be a point in the set (c – 1, c + 1) ∩

(E – {

}). Pick such a point y

in the set. This point must appear in the sequence

at least once. Hence, there is an index n

such that

(8.14)

In general, suppose we have found

such that

Since the set

(

– {

}) contains infinitely many points and the sequence x

, . . . ,

has only

terms, we can pick a point

–

{

}) such that According to mathematical induction, a subsequence

is obtained such that x

Thus,

(8.15)

When k → ∞, 1/k

→

0. Thus, lim

= c.

Look at the proof here. If the subsequence

can be obtained by mathe-

matical induction, then the recursive procedure in the vase puzzle can analogously

be finished. That is, if “there is no way to finish the procedure,” as posited in

Explanation 2, the proof given must be incorrect. Some may argue that the proof

above is not the only one for the theorem. If so, let us look at the following

well-known argument of Cantor.

Example 8.6.3 [Halmos (1960)]. One of the greatest proofs in set theory shows

the following amazing result: The set of all real numbers that are greater than zero

and smaller than 1 has greater cardinality than the set of all natural numbers.

Unreasonable Effectiveness of Mathematics: A New Tour

185

Proof: Obviously, the set and the set of all real numbers between 0 and

1 are infinite sets. By contradiction, suppose That is, there exists a

one-to-one correspondence ƒ : For any q

∈ let a

= q if ƒ(

) = q for

some n

∈

Thus, the elements in can be written as a sequence

(8.16)

Since each q ∈ satisfies 0 < q < 1, it is possible to write the elements in as

(8.17)

where each a

is a digit in the set W =

{0,1,2,3,4,5,6,7,8,9}. Now let b be a

number with expression

(8.18)

such that each

∈ W and that for each

∈

≠

. That is, b ∈

and

not in the list (8.17). This contradicts the assumption that each element of

is in

the list (8.17). Hence,

Even though this proof does not mention mathematical induction, the existence

of the number b does depend on the principle. To be more specific, the number b

needs to be constructed as follows:

Initial step: Define b

being a number ∈ A – {

Inductive step: Suppose for n

∈

the

’s have been defined for all k < n.

Then let b

be a number

∈

–

{

By mathematical induction, for each natural number n a number b

can be

chosen. If this inductive process “can be finished,” the desired number b can be

constructed in the form of Eq. (8.18). Once again, if “there is no way to finish

the procedure,” there is no way to finish choosing the b

’s. Consequently, there is

no way to construct b in Eq. (8.18). That is, Cantor’s diagonal method, which we

have just described, is invalid.

A seasoned mathematician can see that the principle of mathematical induction

has been and will be “used” or “abused” in ways as we have described. Thus, one

or both of the following is true: (1) Explanation 2 is incorrect. (2) In the cases

described, the principle of mathematical induction has been abused.

Conjecture 8.6.1. Statement (1) is true while statement (2) is not.

186

Chapter 8

Table 8. 1.

Age

Age Sum

Product

72 74 72

39 72

23 72

18 22

15 72

14 72

18 72

13 72

14 72

8.6.4. Some Threatening Impacts of the Vase Puzzle

The first explanation is a great and fruitful resource of ideas that connect the

vase puzzle with problems in philosophy, methodology and epistemology. In this

subsection, we discuss these connections.

8.6.4.1. Connections with methodology. In general, if known information

about a phenomenon has not all been used, the phenomenon can either not be

understood because of lack of knowledge or be understood at a more global level

and more information is needed to be more specific. For example [see (Billstein

et al., 1990) for details], when his students asked Mr. Factor what his children’s

ages were, he said, “I have three children. The product of their ages is 72, and

the sum of their ages is the number of this room.” The children then asked for the

door to be opened to verify the room number, which is 14. Then, Sonja, the class

math whiz, told the teacher that she needed more information to solve the problem.

Mr. Factor said, “My oldest child is good at chess.” Then, Sonja announced the

correct ages of Mr. Factor’s children as: 3,3,8. Based on the given information,

Sonja constructed Table 8.1. She knew the sum of the ages was 14, but could not

determine the correct answer from the two choices (2,6,6) and (3,3,8). When

Sonja was told that the oldest child was good at chess, she knew that (2,6,6) could

not be a possible combination because if the children were 2, 6, and 6 years old,

there would not be an oldest child.

Notice that the vase puzzle does not satisfy the general methodology of recog-

nition. The information about ordering really made understanding more contro-

versial rather than more specific.

Unreasonable Effectiveness of Mathematics: A New Tour

187

Our vase puzzle does not fit into categories of problems considered by Polya

(1973). The problem is neither a “perfectly stated” nor “practical.” It is concep-

tual and thought-provoking. It challenges traditional mathematical reasoning. It

especially raises questions about the idea of mathematical modeling.

8.6.4.2. Connections with epistemology. Through history, the development

of scientific theories and the understanding of realities have been hand in hand.

To know more about nature, scientists establish hypotheses and develop theo-

ries. These theories further our understanding of nature and, in turn, push the

development of the theories to a higher level.

Among the most common practices of modern scientific activities is the science

and technology of data analysis. It is known in analysis that the more data that are

collected, the more misleading the conclusion that will be obtained, measuring and

collecting each datum are subject to errors or noise, and an extraordinary amount

of noise can easily conceal the actual state of a phenomenon. The vase puzzle

is another example showing that the more facts we know, the more confused

we become. At the same time, the vase puzzle also questions the accuracy of

scientific predictions, because the ignorance of a fact will lead to a completely

different prediction. Therefore, one could question the value and the meaning of

scientific research and scientific predictions.

8.6.4.3. Connections with philosophy. Studying nature and the structure of

time and space is an ancient interest. The vase puzzle, the paradox of the hotel,

and the paradox of a moving particle, once again, raise the interest of exploring

the answer to the question, because by reassigning some numbers, an infinite

procedure can be finished within a randomly chosen time frame, an infinitely large

piece of paper can be shrunk to any desired size, and an infinitely high building

can be rebuilt in order to fit into a limited space. Then we ask: Are the structures

of space and time continuous? What is the meaning of volume?

Maybe the answer to the second question is that the concept of volume is

meaningless mathematically because one can prove that it is possible to chop a

solid ball into small pieces and then reassemble these pieces into as many balls as

one desires of the same size as the original ball (Jech, 1973).

As for the first question, about the continuity of space and time, we think the

structure of the set of all hyperreal numbers (Davis, 1977) describes and explains

the hotel and moving particle paradoxes better than the commonly accepted one.

For example, the commonly accepted model for time is the set of all real numbers,

which is continuous and complete. The property of completeness of real numbers

was applied to model the process of crystallization of polymers (Lin and Qiu, 1987).

If the structure of hyperreal numbers is applied, the modeling for the crystallization

in (Lin and Qiu, 1987) would no longer be correct. To make things more specific,

let us describe the structure of the hyperreal numbers in some detail.

The concept of hyperreal numbers is a product of nonstandard analysis. This

theory deals with ideal elements and is a time-honored and significant mathematical

188

Chapter 8

theory. These ideal elements include “numbers” that are infinitely close to the

numbers we are interested in and those that are infinitely far away from all real

numbers.

Briefly speaking, the set

of all hyperreal numbers has operations +, – , × ,

and a linear ordering relation <. Let

⏐

be the absolute value of a hyperreal number

x ∈

Then

⏐

= max{

x, -x

}, and

is made up of three parts:

(8.19)

(8.20)

and

– F, where F contains all finite hyperreal numbers, I is the set of all

infinitesimals, and – F includes all infinite hyperreal numbers.

The set of all real numbers is a dense subset of F. Geometrically, F can

be obtained as follows: For each real number r

∈ the number r in has a

neighborhood

(8.21)

such that for any real numbers r, s ∈

and infinitesimals

y ∈ I, r < s , if and

only if r + x < s + y. This neighborhood r

⊕ I is called the monad of r. It can be

seen that all monads of real numbers are densely ordered.

The set – F of all infinite hyperreal numbers consists of F as the center

“block,” and, in either the positive or the negative directions, an ordered set of

“blocks.” These blocks are densely ordered with neither a first nor last element.

Each block has the same geometric structure as F and is termed a galaxy.

is used to model time and the Cartesian product to model space,

Questions 8.6.2 and 8.6.3 can be answered as follows:

A. For (Benardete) Question 8.6.2: Suppose the hotel roof is r feet high.

When the roof is removed, nothing can be seen if one looks at the hotel from above

because what a person sees should be in the layers r – x for each x ∈ I and x > 0,

and no guests live on these levels (no floor reaches these heights).

B. For Question 8.6.3: Since a seemly smooth moving particle really jumps

forward from a monad to another, it could meet any point in the sequence (8.10)

first.

8.7. Final Comments and Further Questions

From our discussion it can be seen that there are roughly two methods to intro-

duce new mathematical concepts. One is that in the study of practical problems,

new mathematical concepts are abstracted, and the other is that in the search for

relations between mathematical concepts, new concepts are discovered. The ap-

plication of mathematics, as shown by the examples, brings life to the development

Unreasonable Effectiveness of Mathematics: A New Tour

189

of mathematics so that when dealing with real problems, mathematics often makes

us better understand the phenomena under consideration. If all well-developed

mathematical theories do not fit a specific situation under consideration, a modi-

fied mathematical theory will be developed to study the situation. That is to say,

mathematics, just as all other scientific branches, is developed in the process of

examining, verifying and modifying itself.

When facing practical problems, new abstract mathematical theories are de-

veloped to investigate them. At the same time, predictions based on the newly

developed theories are so accurate that the following question appears:

Question 8.7.1. Does the human way of thinking have the same structure as that

of the material world?

On the other hand, the mathematical palace is built upon the “empty set.”

History gradually shows that almost all natural phenomena can be described and

studied with mathematics. From these facts the following question arises.

Question 8.7.2.

If all laws of nature can be written in the language of mathematics,

can we conclude that the universe we live in rests on the empty set, just as Genesis

1:1 states that “In the beginning, God created the heaven and the earth. And the

earth was without form, and void”?

CHAPTER 9

General Systems: A Multirelation

Approach

Based on the previous chapter, it is time to study the concept of general systems

mathematically. The concept of systems is a generalization of that of structures.

Generally speaking, a system consists of a set of objects and a set of relations

between the objects, and has a structure of “layers.” In this chapter, a model

of general systems is introduced, based on the methods of set theory, and some

basic global properties of systems are studied in detail. The chapter contains

eight sections. In the first section, layer structures, the existence of fundamental

objects, the finite chain condition, and centralized systems are studied. The

second section consists of properties of relations between systems, the structure

of quotient systems, and a characterization of centralizable systems. Methods of

constructing new systems, based on a set of given systems, are introduced in the

third section. These methods serve as a mathematical foundation for the analysis

of “whole–parts” relations:

In the fourth section, the structure of connected systems is studied and used

to check the connectedness of newly constructed systems. This structure shows

whether a system can be seen as a set of systems or a single system only. In the

fifth and the seventh sections, hierarchies of systems (or, say, large-scale systems)

are studied. The concepts of controllabilities of general systems are introduced

and studied in the sixth section. Some references are listed in the last section.

9.1. The Concept of General Systems

Let A be a set and n an ordinal number. An n-ary relation r on A is a subset of

the Cartesian product A

In the sequel, A

means either the Cartesian product of

n copies of A or the set of all mappings from n into A. From Chapters 2 and 3 it is

easy to see that the two definitions of A

are equivalent.

If r is a relation on A, there exists an ordinal n = n(

), a function of r, such

191

that

192

Chapter 9

⊆

The ordinal number n = n(

) is called the length of the relation r. When r is the

empty relation assume that

(

) = 0; i.e., the length of the relation

is 0.

S is a (general) system if S is an ordered pair (M

R) of sets, where R is a set

of some relations on the set M. Each element in M is called an object of S, and M

and R are called the object set and the relation set of S, respectively. The system

S is discrete if R =

R = {

}

and M ≠ . It is trivial if M =

Two systems S

= (

, R

= 1,2, are identical, denoted S

= S

, if

and R

= R

The system

is a partial system of the system

⊆

and for each relation

∈ R

there exists a relation r

∈

such that

⏐

, where r

2⏐

is the

restriction of

on M

, and is defined by

The system

is a subsystem of

⊆

and for each relation

∈

there

exists a relation

∈ R

, satisfying

⊆

⏐

Theorem 9.1.1. There is no system such that the object set of the system consists

of all systems.

This is a restatement of the Zermelo–Russel

paradox.

Proof: Consider the class V of all sets. For each x ∈ V define a system by

(

). Then a 1–1 correspondence h is defined such that h(x) = (x, ). If there

is a system S = (

, R) whose object set contains all systems, then M is a set.

Therefore, the Axiom of Comprehension shows that V is a set, contradiction.

A system

= (

, R

) is an

th-level object system of

= (M

, R

) if there

exist systems S

= (M

), for

= 1,2, … ,

–1, such that

is an object in M

i –1

1 ≤ i ≤ n. Each element in M

is called an nth-level object of S

Theorem 9.1.2 [ZFC].

Let S

= (M

, R

) be a system and S

= (M

, R

) an nth-

level object system of S

Then S

cannot be a subsystem of S

for each natural

number n

∈

Proof:

The theorem will be proved by contradiction. Suppose that for a certain

natural number

, the system S

is a subsystem of the n

th-level object system

General Systems: A Multirelation Approach 193

Let S

= (

) be the systems, for i = 1, 2, … ,n – 1, such that S

∈ M

i–1

= 1, 2, . . . ,

n. Define a set X by

From the Axiom of Regularity, it follows that there exists a set Y

∈ X such that

∩ X=

There now exist three possibilities:

(i) Y = M

for some i.

(ii) Y = S

for some i.

(iii) Y = {M

} for some i.

If possibility (i) holds, There-

fore,

contradiction. If (ii) holds,

and contradiction. If (iii) holds,

contradiction.

These contradictions show that

cannot be a subsystem of S

A chain of object systems of a system S is a sequence for some

ordinal number

, of different-level object systems of S, such that for each pair

j < α with i < j, there exists an integer n = n(

), a function of i and j, such

that

is an n

th-level object system of

. A similar proof to that of Theorem 9.1.2

gives the following.

Theorem 9.1.3 [ZFC]. Each chain of object systems of a S must be finite.

Theorem 9.1.4 [ZFC]. For any system S, there exists exactly one set M(S) con-

sisting of all fundamental objects in S, where a fundamental object in S is a level

object of the system S which is no longer a system.

Proof: Suppose that S = (

, R

). Define

= {

x ∈ M

is not a system}

and

Then *

and

are sets.

Suppose that for a natural number

, two sequences {*

: i = 0, 1, 2, … ,

}

and { : i = 0, 1, 2, … , n

} have been defined such that

is not a system}