Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

152

Chapter 7

It is true that the sequence

satisfies the condition that if

(

, y

) ∈ g, then p > q. If not, then q ≥ p. Hence, there exists a subsequence

such that

Now take the finite sequence w

, w

, . . . , w

, for n = q – p + 1, such that

= y

k+p

, if 0 < k < n – 1 and w

= y

. It can be seen that (w

i–1

, w

)

∈

for i = 1, 2 , . . . , n, and w

, which contradicts the fact that g is strongly

antisymmetric. Therefore, p > q.

To complete the proof, we show that the elements

differ from

one another, contradicting that W is finite. The contradiction thus implies that

⊆ W

must be strictly strongly antisymmetric. To this end, suppose that the

elements of

do not differ. There then exist p

∈

such that p < q,

= y

, and (y

) ∈ g. Hence, (

) ∈ g so that q < p + 1; i.e., q ≤ p

contradicting the fact that p < q. Therefore, is an infinite set, which

contradicts the assumption. This ends the proof of the theorem.

The proof of the previous theorem actually says that strictly strong antisym-

metry implies strong antisymmetry, and that when the set W is finite the converse

implication is also true.

Question 7.7.1.

Construct an example to show that the concept of strong antisym-

metry is different from that of strictly strong symmetry.

For any subset X

⊆ E, define

and

W* = g * W

(7.17)

(7.18)

Lemma 7.7.1 [Qin (1991)]. For any

Proof: For any

there exists

such that w = ƒ

(

). Equation

(7.17) implies that based on which Eq. (7.14) implies that

w = ƒ

(

) ∈ ƒ

(

) and that for any x ∈ ƒ

(

), x ≠ w implies (w

)

∉

The

last condition means that

Therefore, we have shown that

Conversely, for any Eq.(7.14) implies that for

some e ∈ E

, and that for any

implies (w

x) ∉ g. This condition

implies that

That is, we have shown that

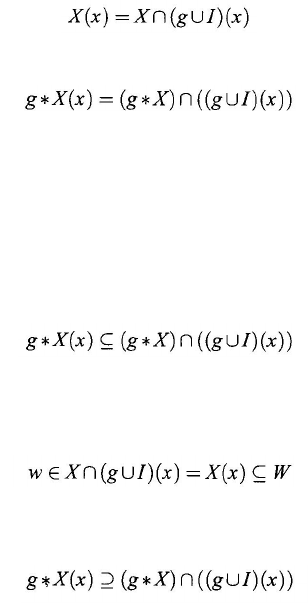
Bellman’s Principle of Optimality and Its Generalizations

153

Lemma 7.7.2 [Qin (1991)]. For any element x ∈ W and subset X ⊆ W, define a

subset X

(

x) ⊆ W by

Then

where I is the diagonal of the Cartesian product X

², defined by I = {(x, x) : x ∈ X

Proof: For each w ∈ g

(

x), w ∈ (

∪

) (x) and for any w' ∈ X

(

x), w' ≠ w,

(

w, w') ∉ g. To show that w ∈ (g

)

∩

(

∪

)(

x), one need only prove that

∈ g

X. If w ∉ g

X, there exists w" ∈ X such that w ≠ w" and (w, w") ∈ g ;

i.e., w"

∈ X

(

x). Therefore, there exists w" ∈ X

(

x) such that (w, w") ∈ g, which

contradicts w

∈ g

(

x), so w ∈ g

X. Thus, we have obtained that

Conversely, for an element w

∈ (g

)

∩

((

∪

I) (x)), w ∈ g

X and w ∈

∪

)(

x). It follows that w ∈ X, w ∈ (g

∪

)(

x), and that for any y ∈ (g

∪

I)(x),

≠ y implies y ∉ X. It is clear that

Therefore, for any

∈

(

∪

)(

x), y ≠ w implies y ∉ X. Hence, w =X

∩

(

∪

I)(w);

i.e., w

∈ g

(

x). The following inclusion relation is thus true:



Lemma 7.7.3 [Qin (1991)]. If g is a strictly strongly antisymmetric relation on

the set W, and Ø

≠ X ⊆ W, then

≠

Proof: The proof is by contradiction. Assume that there exists a subset

≠ X ⊆ W such that g

X = Ø, and let x ∈ X, then x ∉ g

X = Ø. From Eq. (7.14)

it follows that there exists x

∈ X such that x ≠ x

, (

x, x

) ∈ g, and x

∉ g

that there exists x

∈ X such that x

≠ x

, (x

) ∈ g, and x

∉

X, and so

on. Therefore, an infinite sequence x

, . . . has been obtained, satisfying

(

+ 1

) ∈ g, for each i = 1, 2, 3, . . . This condition contradicts the assumption g

is strictly strong antisymmetric. Thus, the proof is complete.



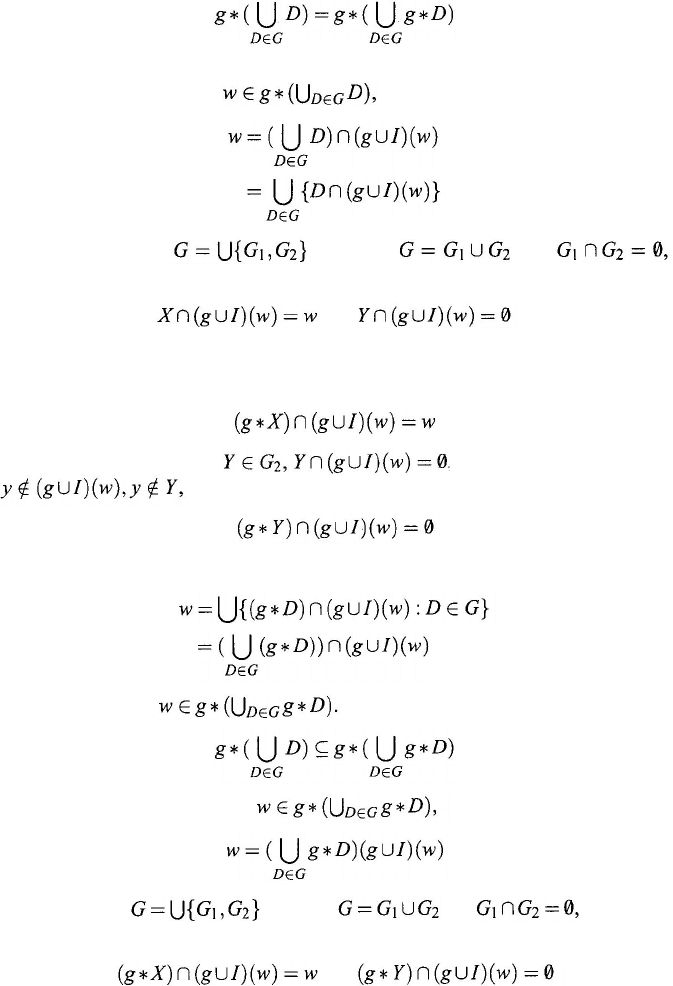
154 Chapter 7

Theorem 7.7.2 [Qin (1991)]. Let g be a strictly strongly antisymmetric relation

on the set W, and G

⊆ p

(

W), the power set of W. Then

Proof: For an element it follows from Lemma 7.6.1 that

Partition the subset such that

and

satisfying, for any X ∈ G

and

∈

and

Therefore, for any X

∈ G

, w ∈ g

X, and for any w ≠ y ∈ g

(

w), one has that

∈ X. Hence y ∉ g

X. That is,

On the other hand, for any it can be seen that for any

and so

∉

Y. That is, for any Y

∈ G

Thus,

which implies that It has thus been shown that

(7.19)

Conversely, for an element

Partition the set

such that

and

satisfying,

for any X

∈ G

, and Y ∈ G

and

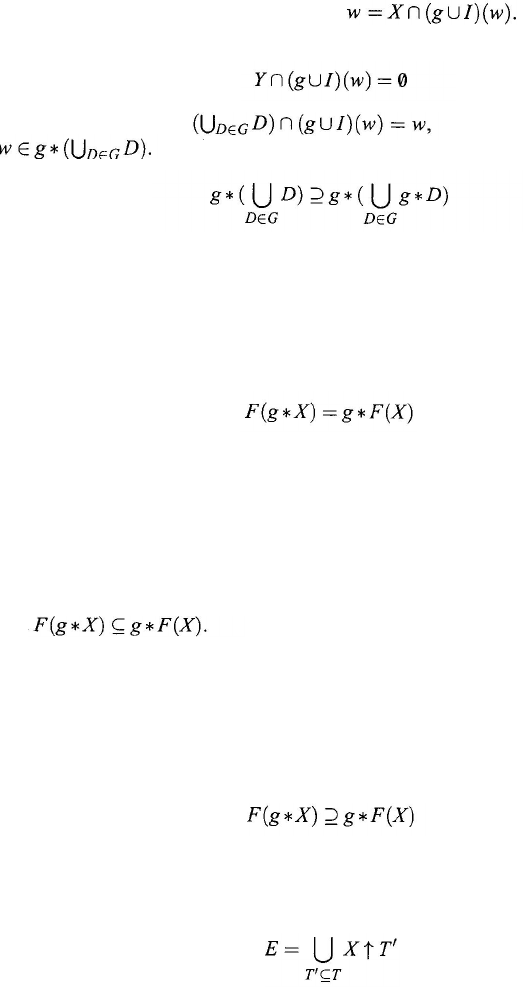
Bellman’s Principle of Optimality and Its Generalizations

155

Hence, for any X ∈ G

, w ∈ g

X; i.e.,

It follows from

Lemmas 7.7.1 and 7.7.3 that for any Y

∈ G

Then one obtains that

which in turn implies that

That is,

(7.20)

Combining Eqs. (7.19) and (7.20), proved the theorem.



Theorem 7.7.3 [Qin (1991)]. In the optimization model (W, E; ƒ, g) of general

systems, if F : W

→ W is a strictly order-preserving mapping and X is a subset of

W, then

Proof:

For an element w ∈ F(

X), there exists y ∈ g

X such that w =

(

y) ∈ F

(

X) and such that for any z ≠ y, (y, Z ) ∈ g, so z ∉ X. It suffices to show

that there is no F(w

) ∉ F

(

X) satisfying w = F(w

) and F

(

) ≠ F (

), such

that (

(

y), F

(

)) ∈ g. Suppose there is such an element F(w

) ∈ F

(

X). It then

follows that (

y, w) ∈ g and y ≠ w

, which contradicts the assumption that

∈

and implies that w

∈ g

(

X). From the arbitrariness of the element w, it follows

that

Conversely, for any element

∈

(

X), there exists an element y ∈ X such

that w = F

(

y). It suffices to show that there is no z ∈ X such that z ≠ y and

(

y, z) ∈ g. Suppose this condition is not satisfied. Then from the strictly order-

preserving properties of F, it follows that F

(

y) ≠ F

(

z) and (

(

y), F

(

z)) ∈ g. This

contradicts the assumption that

∈

(

). Hence, y ∈ g

; i.e.,

∈

(

X ).

Again, the arbitrariness of the element w guarantees



Let W, X, and T be nonempty sets with g ⊆ W² given. Define

A mapping ƒ :

→

is called

-resolving, if there exists a mapping

∪

W² →

W satisfying

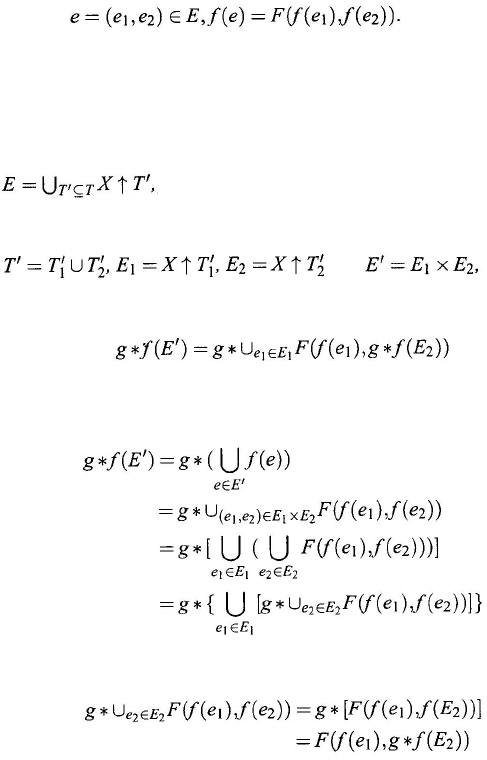
156

Chapter 7

(i)

F (

) = w for each w ∈ W.

(ii)

For any

(iii)

For any w ∈ W, the mappings F

(

w, ·) and F(·, w) : W → W are strictly

order-preserving.

Theorem 7.7.4 [Qin (1991)]. If the optimization model (W,E;ƒ,g) of general

systems satisfies

(i)

for some given nonempty sets X and T,

(ii)

ƒ : E → W is p

-resolving,

(iii)

and

then

(7.2 1)

Proof: It follows from Theorem 7.7.2 that

For fixed e

∈ E

, it follows from Theorem 7.7.3 that

Therefore, Eq. (7.21) is valid. 

By Theorem 7.7.1 it follows that Theorem 7.7.4 holds with W strongly anti-

symmetric if W is finite.

Let (W, E;ƒ ,g) be a given optimization model of general systems with the sets

W and E nonempty. The optimal solutions of (W,E;ƒ,g) are called the zeroth-

order optimization solutions of the system (

W, E ;ƒ, g

) .

The first-order optimization

solutions of the system (W, E;ƒ ,g

)

are the optimal solutions of the subsystem of

(

W,E;ƒ,g) obtained by removing all zeroth-order optimization solutions from

the original system (W,E;ƒ,g). Inductively, the nth-order optimization solutions

Bellman’s Principle of Optimality and Its Generalizations

157

of (W,E

;ƒ,

) are the optimal solutions of the subsystem obtained by removing

all zeroth-order, first-order, . . . ,

(

n – 1)st-order optimization solutions from the

original system (W,E

;ƒ,

). If e ∈ E is an n th-order optimization solution of

(

W,E;ƒ,

), the number n, which is a function of the optimization solution e and

is denoted by n = Oo

(

), is called the optimization order of the solution e.

Define

= W

and

= W

– 1

–

for each i ∈

– 1

Each element

∈

is called an i

th-order generalized extreme value of

Theorem 7.7.5 [Qin (1988)]. If the optimization model (W,E

;ƒ,

) of general

systems satisfies the conditions

(i) W and E are nonempty,

(ii) ƒ : E → W is p-resolving; and

(iii) g

⊆ W

is strongly antisymmetric,

then the sum of the optimization orders of all subpolicies is less than or equal to

the optimization order of the policy itself.

The proof is left to the reader.

7.8. Applications

(i) In Hu’s counterexample it can be shown that θ

satisfies the optimum-

preserving law, and that

is associative but not distributive over θ

. Therefore,

Theorem 7.4.2 says that Bellman’s Principle of Optimality does not hold. At the

same time, by Theorem 7.5.2, it follows that the fundamental equations will not

give the global optimum solution. For details one has that

with

→

→ C → D

→ E its policy, and

with

→

→ C → D

→ E the global optimum policy. Here,

(ii) Consider the network in Fig. 7.2. Let

= maximum and θ

∧

. That is,

for any x,y

∈ W, θ

(

x,y) = min{x,y}. Then A → B

→

→ D is an optimum

158

Chapter 7

Figure 7.2. The principle of optimality does not hold.

path with weight 2, but its subpath

→ C

→ D is not optimum, since its weight

is 3 and the weight of B

→ C

→ D is 2. It can be shown that θ

is associative

but does not satisfy a cancellation property. From Theorem 7.4.1 it follows that

the Generalized Principle does not hold in this case.

(iii) Consider the network in Fig. 7.2 again with

= subminimum and

= +.

That is,

is the regular addition, and

is defined as

θ1

(

X) = min{

– {min{

}}}

= the second minimum in X

for each X

∈ p(W

) with

⏐

X⏐ > 1. Then A → B

→ C

→ D is the optimum path

with weight 6, while its subpolicy

→ C

→ D with weight 4 is not optimum. It

can be seen that

is associative and distributive over

, but θ

does not possess

an optimum-preserving property. For example,

(iv) For a sequential decision process, the system (

;

,θ

) can be defined

as follows:

W = set of all possible weights

= optimum choice rule

= operation between weights

G = the set of all states of the process

Define a network g

∈ W ↑ G

such that, for any x, y ∈ G, g

(

x,y) = w iff the cost

(or profit) from the state x to the state y is w. If a state y is not accessible from a

state x, then define g(x,y) = the zero element in W. If the process has n stages,

is the initial state and a

is the terminal state. Then g

〈

〉

(

) is simply the

cost (or profit) of a global optimum decision. If

Bellman’s Principle of Optimality and Its Generalizations

159

then a

, . . . ,

is the optimum sequential decision required. For a subpolicy

+ 1

, . . . ,

, where 0 ≤ i < j ≤ n, the Generalized Principle of Optimality says

that if

satisfies the optimum-preserving law and θ

satisfies the associative,

cancellation, and distributive laws over

, then a

+ 1

, . . . ,

must be optimum

with regard to the initial state a

and the terminal state a

In the shortest-path, inventory, and traveling-salesman problems (Dreyfus

and Law, 1977), the system considered is ( min, +). In the equipment-

replacement models and the resource allocation problems (Dreyfus and Law, 1977),

the system of interest is ( max, +). It can be shown that ( min, +) and

( max, +) satisfy the Generalized Principle of Optimality (Theorem 7.3.1).

Thus, Bellman’s Principle of Optimality holds in these optimization problems,

and can be solved by dynamic programming. At the same time, it can be shown

that “min” and “max” satisfy the optimum-preserving law and that “+” satisfies

the cancellation, associative, and distributive laws (over “min” or “max”). Thus,

Theorem 7.5.1 says that in ( min, +) and ( max, +) the desired optimum

solutions can be obtained by applying fundamental equations.

The following propositions and theorem reveal the relation between the fun-

damental equation approach and the generalized principle of optimality.

For convenience, a system (

W,G

;θ

, θ

), as defined in Section 7.3, is re-

cursive if for any g

∈ W ↑ G

, n ∈ , and

That is, being recursive is equivalent to having the fundamental equation ap-

proach hold. The system (W,G

;

) satisfies the optimum-preserving law if

for any g

∈ W ↑ G

, n ∈ , and a

, . . . ,

∈ G, the following is true: if

the zero element of W, then for any 0

≤

j ≤ n,

Intuitively speaking, (

W, G;

) satisfies the

optimum-preserving law means that the generalized principle of optimality holds.

Proposition 7.8.1 [Wu and Wu (1986)]. The recursiveness of the system

(W, G

;

) does not imply that it satisfies the optimum-preserving law.

Proof: It suffices to construct an example to show that a recursive system

(

W, G

;

) does not satisfy the optimum-preserving law. Let W is the set of all

nonnegative real numbers, G be a subset of real numbers,

is the maximum, and

is the minimum. It is evident that θ

satisfies the optimum-preserving law and

satisfies the associative and distributive laws over

. So, according to Theorem

7.5.1, (

W, G

;

,θ

) is recursive, but it does not satisfy the optimum-preserving

law. See the network in Fig. 7.2.



Proposition 7.8.2 [Wu and Wu (1986)]. The optimum-preserving property of the

system (W,G

;

)

does not imply the recursiveness of the system.

160

Chapter 7

Figure 7.3. Optimum-preserving law does not imply recursiveness.

Proof: Again, it suffices to show the proposition by constructing a counterex-

ample. Consider the system (W,G

;

), (Fig. 7.3), where

W = the set of all nonnegative real numbers

(

) =

{

subminimum of X

⏐

> 1

if X = {

}

= + (regular addition)

Then it can be seen that the element

∈

↑

(Fig. 7.3) satisfies

〈

〉

(

A,D ) = 4

and A

→ B

→

→ D and is the optimum policy, of which all subpolicies

are optimum.

That is, the system possesses a (

;3,

A,D ) optimum-preserving

property. However, from the fundamental equation [Eq. (7.9)], it can be computed

that

〈

〉

(

A,D ) = 5

with A

→ B

→ C

→

its corresponding policy. Since

the system does not possess (

;3,

A,D)-recursiveness.



Theorem 7.8.1 [Wu and Wu (1986)]. In the system (W,G

;

) with θ

satis-

fying the optimum-preserving law and

satisfying the cancellation, associative,

and distributive laws over

both the optimum-preserving law and the recursive

law hold. That is, in this special system the fundamental equation will give a

global optimum solution, and the generalized principle of optimality holds.

The result is a consequence of Theorems 7.5.1 and 7.3.1.

Bellman’s Principle of Optimality and Its Generalizations 161

7.9. Conclusion

This chapter generalizes the fundamental idea of dynamic programming to the

widest sense available today in the research of systems science and pansystems

analysis. For example, the first approach generalized the ideas of Bellman’s

Principle of Optimality and of the fundamental equations in dynamic programming

to generalized weighted networks, where for any nonempty sets W and G each

element g

∈ W ↑ G

is called a generalized weighted network with weights in W

and nodes in G. The second approach will surely open up a new era of research to

study the idea of optimization in the theory of general systems.

In addition to the set of real numbers being used as the criteria set, gen-

eralized dynamic programming assume all other possible sets as criteria sets,

such as vectors, matrices, tensors, and so on. Actually, there have appeared

some studies and applications of vector-valued dynamic programming (Brown

and Strauch, 1965; Furukawa, 1980; Denardo, 1967; Henig, 1983). In these

works, Bellman’s Principle of Optimality in the dynamic vector-valued models

has also been discussed and similar results obtained. These facts are helpful in

showing the universal significance of the approaches presented in this chapter.

Bellman’s Principle of Optimality has been generalized to the Generalized

Principle of Optimality and the Operation Epitome Principle. It may be expected

that in dealing with optimization problems of the most general sense, especially

with those out of the ordinary, the Generalized Principle of Optimality and the

Operation Epitome Principle will play important roles.

Practically, the main point of dynamic programming is to use the fundamental

equations to compute a desired optimal solution. However, in many practical op-

timization problems, especially those with nonscalar-valued performance criteria,

their underlying structure of systems is much more complicated than (

min, +)

and (

max, +). In those cases, the method of classical dynamic programming

may not apply. In this chapter, a criterion has been established to decide whether

the approach of fundamental equations can still be employed.