Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

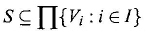
122

Chapter 6

6.2. Multilevel Structure of Nature

Even though the major part of classical and modern mathematics deals with

subject matters of one level, such as problems on the real number line, the plane,

the n-dimensional Euclidean spaces, etc., human minds have been searching for

the organic structure of multilevels of the universe since at least the time of the

one-element Ionians (624–500 B.C.). For example, in the search for order, Ionians

had a naturalistic and materialistic bent. They sought causes and explanations

in terms of the eternal working of things themselves rather than in any divine,

mythological, or supernatural intervention. Looking for a single basic reality,

each Ionian believed that all things have their origin in a single knowable element:

water, air, fire, or some indeterminate, nebulous substance. For more on this,

see (Perlman, 1970). This section shows that general systems theory, based on

Cantor’s set theory, first introduced formally by Mesarovic in the early 1960s, can

be seen as a new research approach to the multilevel structure of nature.

Mesarovic’s definition of a general system is as follows (Mesarovic and Taka-

hara, 1975):

A system S is a relation on nonempty sets V

where I is an index set.

This structure of general systems is multilevel, since elements in the nonempty

sets

could be systems also. Using this idea inductively, we see that an element

of the system S could be a system, an element S

of system S

could be a

system, . . . Can this process go on forever? If the answer to the question is “yes,”

then “the world would be infinitely divisible”?! If the answer to the question is

“no,” does that mean the world is made up of fundamental elements?

The idea that the world is infinitely divisible can be found in Anaxagoras’

“seeds” philosophy (510–428 B.C.). He was unwilling to submerge the tremen-

dous varieties of things into any common denominator, and preferred to accept the

immediate diversity of things as is. With his philosophy, every object is infinitely

divisible. No matter how far an object is divided, what is left would have char-

acteristics of the original substance. The opposite idea — that the world is made

up of fundamental particles — appeared from 500 to 55 B.C. The Leucippus–

Democritus atom combined features of the Ionians’ single element, Anaxagoras’

“seeds,” and some thoughts of other schools, and yet was an improvement over

all of them. “Atom” means “not divisible” in Greek. This term was intentionally

chosen by Democritus to emphasize a particle so small that it could no longer

be divided. To Leucippus and Democritus, the universe originally and basically

consisted entirely of “atoms” and a “void” in which atoms move.

A Mathematics of Computability that Speaks the Language of Levels

123

In the search for an answer as to which of the two opposite ideas could be

right, Ma and Lin (1987), introduced the following definition of general systems:

S is a (general) system, if S is an ordered pair (M,R) of sets, where R is a set of

some relations defined on M. Each element in M is called an object of S, and M

and R are called the object set and the relation set of S, respectively. For each

relation r

∈ R, r is defined as follows: there exists an ordinal number n = n(r),

depending on r, such that r

⊆ M

, that can be either finite or infinite, and called

the length of r. Assume the length of the empty relation is 0; i.e., n( ) = 0. This

new definition of general systems generalizes that of Mesarovic. Many important

structures of systems can now be studied that otherwise could not have been with

the one-relation approach. We note that the concept of general systems was defined

in more general terms by many other authors as well. For example, Wu and Klir

independently defined the concepts of pansystems and systems at a much higher

level. For more details see (Wu, 1994; Klir, 1985).

Two systems S

= (M

), i = 1, 2, are identical, if M

= M

and R

= R

System S

is a partial system of system

if M

⊆ M

and for each relation

∈

there exists a relation r

∈

such that r

= r

⏐

= r

∩

(

)

. System S

a subsystem of S

, if M

⊆ M

and for each relation

∈ R

there exists a relation

∈

such that

⊆

⏐

. A system S

= (M

) is an

th-level object system

of a system S

= (M

) if there exist systems S

= (M

), i = 1, 2, . . . , n – 1,

such that S

is an object in M

i –1

, 1 ≤ i ≤ n. Each element in M

is called an

nth-level object of S

Based on these notations, the following mathematical results (Lin and Ma,

1993) can be proved, where (ZFC) means that we assume all the axioms in the

ZFC axiom system (Kuratowski and Mostowski, 1976) are true.

Theorem 6.2.1 [Russell’s paradox].

of the system consists of all systems.

There is no system such that the object set

Theorem 6.2.2 [ZFC]. Let S

= (M

) be a system and S

= (M

) an nth-

level object system of S

. Then it is impossible for S

to be a subsystem of S

for

each integer n > 0.

A chain of object systems of a system S is a sequence {S

: i < α} for some

ordinal number

, of different-level object systems of the system S, such that for

each pair i,j <

α with i < j, there exists an integer n = n(i,j) such that the system

is an nth-level object system of the system S

Theorem 6.2.3 [ZFC]. Suppose that S is a system. Then each chain of object

systems of S must be finite.

Theorem 6.2.4 [ZFC]. For each system S there exists exactly one set M(S),

consisting of all basic objects in S, where a basic object in S is a level object of S

which is no longer a system.

124 Chapter 6

For detailed treatment of these theorems, please refer to Chapter 9.

As introduced by Klir (Klir, 1985), a system is what is distinguished as a

system. We can then do the following general systems modeling: For each chosen

matter, real situation problem, or environment, such as a chemical reaction process,

a system, describing the matter of interest, can always be defined. For example,

let S = (M,R) be a systems representation of a chemical reaction process, such

that M stands for the set of all substances used in the reaction and R is the set

of all relations between the substances in M. It can be seen that S represents

the chemical reaction of interest. Based upon this modeling and Theorems 6.2.3

and 6.2.4, it follows that we have argued theoretically that the world is finitely

divisible.

In (Lin, 1996) or in Chapter 5 the same methodology was used to show that a

theoretical foundation can be established for the Law of Conservation of Matter–

Energy.

6.3.

Some Hypotheses in Modern Physics

Without using a mathematics of multilevels, some hypotheses in modern sci-

ence seem to be contradictory. However, the theories, established on the hy-

potheses, have been winning victories one after another. Einstein’s relativity and

Dirac’s quantum mechanics, for example, are two of these theories. In this section

two such hypotheses are listed to further support the need for a mathematics of

multilevels.

6.3.1.

The Rest Mass of a Photon

rest mass m

According to Einstein, the inertial mass m of a moving particle is related to its

as follows:

(6.1)

where c stands for the speed of light and v is the particle speed. As for the

photon, since its speed is

, the rest mass m

should be zero, or from Eq. (6.1)

m =

∞, contradicting observations. However, even it is assumed that m

= 0, the

fallacy involved in the calculation still remains in Eq. (6.1) because in classical

mathematics on the real number line, 0

÷ 0 is undetermined.

6.3.2.

Dirac’s

δ δ

Function

In Dirac’s well-known work (1958), a function, later named Dirac’s

function,

was introduced as follows: δ : , where is the set of all real numbers,

A Mathematics of Computability that Speaks the Language of Levels

125

satisfies the conditions:

δ(x) = 0 whenever x ≠ 0

δ(0) = ∞

(6.2)

where

(x) is a function on

with compact support and is infinitely differentiable.

This function has played an important role in quantum mechanics. However,

in classical mathematics, including modem measure theory, it is impossible to

have such a function, since each function ƒ

(

x) satisfying the first condition must

possess the property that

Because of the magnificent role that Dirac’s

δ function had played in the

success of quantum mechanics, the international mathematics community became

desperate to come up with a feasible explanation for the strange

δ function. In

1950, Schwartz introduced the concept of distributions, based on which the

function was understood as a linear functional defined on the “elementary space”

consisting of real-valued functions with some special mathematical properties.

For details, see (Richards and Youn, 1990).

6.4. A Non-Archimedean Number Field

In this section a number field, called a generalized number system (GNS), is

introduced. The concept of the GNS is based upon (Wang, 1964), which suc-

cessfully solved an open problem in general topology. Independently, Laugwitz

(1961; 1962; 1968) studied the concept of generalized power series. The concept

of the GNS was first introduced in the early 1980s by Wang (1985; 1991) without

reference to Laugwitz’s work and Robinson’s nonstandard analysis. The GNS

is really a non-Archimedean number field and has found many successful appli-

cations in modern physics. Algebraically, the GNS is a subfield of Laugwitz’s

generalized power series.

Historically speaking, nonstandard analysis, established in the early 1960s

by Robinson (Davis, 1977), first introduced the infinitesimal and infinitely large

numbers formally and legally, based on mathematical logic. This theory broke

through the limitation of the classical concept of real numbers, where infinities

are usually considered ideal objects. With nonstandard analysis, many classical

theories, such as mathematical analysis, algebra, norm spaces, some classical

mechanics problems, etc., can be greatly simplified and become more intuitive.

However, the shortfall of Robinson’s nonstandard analysis is that infinitesimals

and infinities can only be shown to exist and have no concrete expressions of

any tangible form. Based on the argument of the existence of infinitesimals and

126

Chapter 6

infinities given in Robinson’s theory, the GNS has the computational advantage,

since each number here, whether ordinary real, infinitesimal, or an infinity, has an

exact expression in terms of the real numbers in the classical sense.

A generalized number x is a function from to

where

is the set of

all integers and is the set of all real numbers, such that there exists a number

called the level index of x, satisfying

x(t) = 0 for all t < k, and x (k(x))

≠ 0

(6.3)

Then x can be expressed as a generalized power series as follows:

(6.4)

where 1

(

)

stands for the function from

such that 1

(

)

(

s) = 0 if s ≠ t, and

(

)

(

t) = 1 and x(t) ≡ x

. Intuitively, the right-hand side of Eq. (6.4) is the “graph”

of the function x : . The set of all generalized numbers will be written as

GNS.

We now define operations of generalized numbers as follows:

(1)

Addition and subtraction.:

Let x,y be arbitrary from GNS. Define

(6.5)

(2)

Ordering.:

The order relation between x and y

∈ GNS is the lexicographical ordering;

i.e., x < y iff there is an integer k

such that x

(

t) = y

(t) if t < k

and

(

) < y

(3)

Scalar multiplication.:

Let c

∈

and

∈

GNS

define

(6.6)

Because of the ordering relation defined in 2, we can now think of GNS as

a system of numbers of different level; and the function 1

(

will be called

the “unit element” of the tth level.

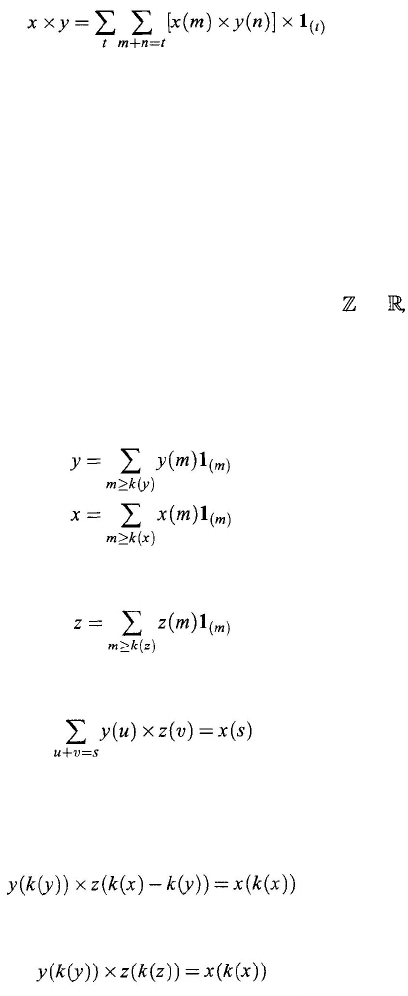
A Mathematics of Computability that Speaks the Language of Levels

127

(4)

Multiplication.:

Let x,y

∈ GNS. Then the product x × y or xy is defined by

(6.7)

Specifically,

(

)

(

)

= 1

(

t+s

)

(5)

Division.:

For x,y

∈ GNS, if there exists a z ∈ GNS such that

× z = x

(6.8)

then the generalized number z is called the quotient of x divided by y,

denoted by x

÷ y or x

Theorem 6.4.1. If y

≠ 0 ≡ ∑

0 × 1

(

)

, the zero function from

then the

quotient x

÷ y always uniquely exists.

Proof: Assume that the known and the unknown generalized numbers

X, y,

and z are

and

We need to find z such that

(6.9)

with

(

)

≤ u ≤ s – k(

) and

(

)

≤ v ≤ s – k (

). This second inequality implies

that we can define

(z) = k(x) – k(y

). Hence, replacing s by k

(x) in Eq. (6.9), we

have

That is,

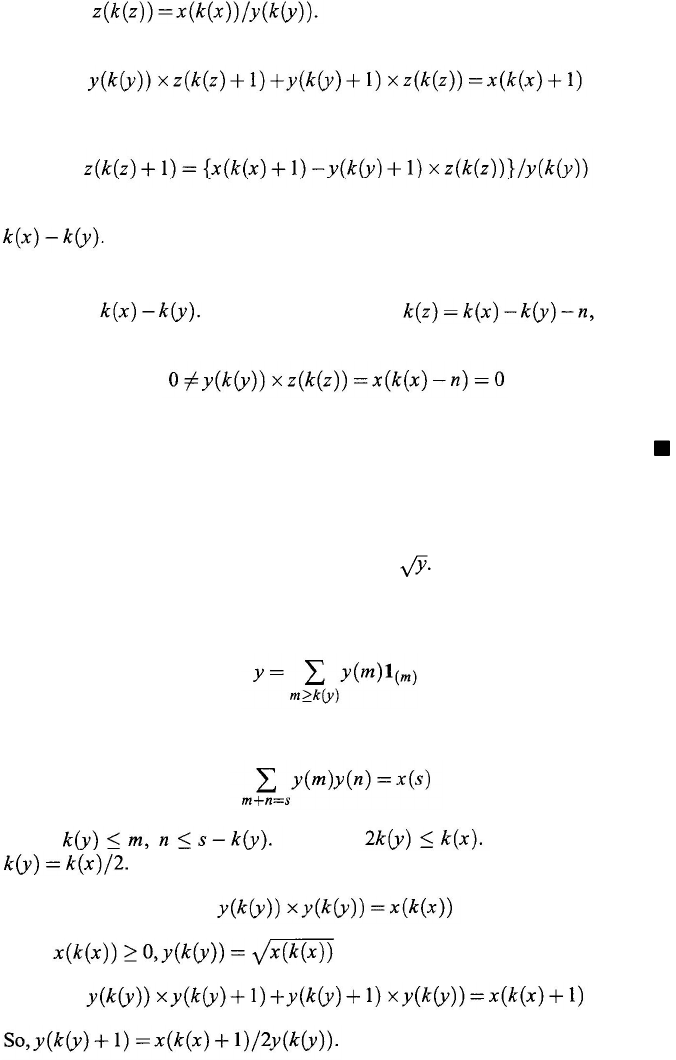
128

Chapter 6

Therefore, When s is replaced by

) + 1 in Eq. (6.9),

we have

Therefore,

By induction, we can continue this process and define each z(

), for m ≥ k

(

) =

Thus, the generalized number z is defined based on the given x and

The uniqueness of

can be shown by observing that the level index of

cannot

be less than

To this end, assume that

for some

nonzero whole number n. Then replacing s by k

(

) – n, in Eq. (6.9), we obtain

contradiction. Therefore, the whole number n must be zero. That is, the general-

ized number z

must be unique.

Theorem 6.4.2. For each x ∈ GNS such that x

(

x)) ≥ 0 and k

(

x) is an even

number, there exists a unique y

∈ GNS such that y² = y × y = x. This generalized

number y is called the square root of x, denoted

Proof: Assume the unknown generalized number y is

Then the equation y × y

= x is equivalent to that for any integer s,

(6.10)

where

That is, We can then define

When s

= k

(

x), Eq. (6.10) becomes

Since

. When s = k

(

x) + 1, Eq. (6.10) becomes

A Mathematics of Computability that Speaks the Language of Levels

To show the uniqueness of y, it suffices to see that k(y) cannot be less than

(

)/2, as defined. To this end, assume for some nonzero

whole number n. Replacing s by k(x) – 2

, changes Eq. (6.10) to

By applying induction on the index

(

)

+ i, the generalized number y can be

well defined.

129

contradiction. That is, the definition of the generalized number y is unique.

The proof of Theorem 6.4.2 can be generalized to obtain 6.4.3.

Theorem 6.4.3.

For each natural number n

≥

and each x

∈

GNS

such that k

)

is a multiple of n, then

(1) If n is even and x(k(x))

≥ 0, there exists a unique y ∈ GNS such that

(2) If n is odd, there exists a unique y

∈ GNS such that y

= x.

The generalized number y in (1) or (2) will be called the nth root of x and denoted

Since y × y = In general, k(y

) =

nk(y), where x

∈ GNS, i =

1,2, ... , n

and

That is, if k(x) is not a multiple of

, there is no y ∈ GNS such that y

= x. In this sense, then Theorem 6.4.3 is the

best we can get.

To conclude this section, let us observe the following facts.

Theorem 6.4.4. (

GNS

, +, ×, <) forms an ordered non-Archimedean field. If

and k and h are integers satisfying k < h, then

the generalized numbers contained in

)

are infinitesimals, compared with those

contained in I

)

; conversely, nonzero generalized numbers in I

)

are infinities

compared with those contained in

)

6.5. Applications

In history, “laws” of the nature have been frequently expressed and treated with

the rigor and beauty of mathematical symbols. For the most part, this application

has been very successful. However, in the past 40 some years, theoretical physicists

130

Chapter 6

have been faced with difficulties in mathematical calculation. According to Wang

(1991), such difficulties arise mainly because the modem world of physics is

multilevel in character, whereas applicable mathematics still remains at the stage of

single level where the only infinities are denoted by –

∞ or +∞

, and are considered

in our macroscopic world as ideal objects and treated with a different set of rules,

compared with those of ordinary real numbers. Now, in GNS, the field

isomorphic to

(0)

, which represents measurable quantities within the macroscopic

world. Also, all numbers in GNS, whether infinities or infinitesimals, are treated

with the same set of rules. In this section we show how the difficulties listed in

Section 6.3 can be resolved with

GNS

6.5.1.

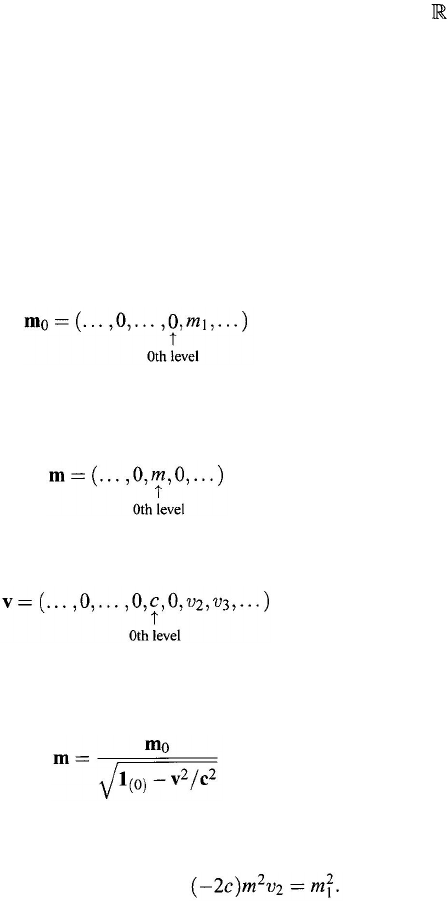
The Hypothesis on the Rest Mass of a Photon

The difficulty in the calculation of

= 0 ÷ 0, discussed in Section 6.3, can be

overcome as follows. Suppose that the rest mass

of a photon is

and that the inertial mass m in Eq. (6.1) is a finite real number; that is, m

∈ I

(0)

has the representation

Now the velocity of a photon is

where v

< 0, since c is assumed by Einstein to be the maximum speed in the

universe. Equation (6.1) can then be written as

where

is understood in the same way as

∈

(0)

. By substituting the

GNS

values

of m

(0)

, v, and c, into this equation, and by comparing the leading nonzero

terms (i.e., the coefficients of 1

(2)

), we obtain

That gives the

relation between

and m

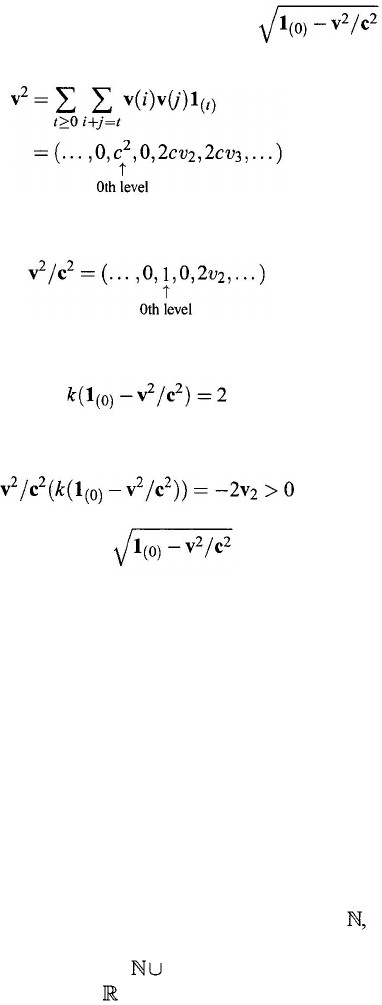
A Mathematics of Computability that Speaks the Language of Levels

131

In this argument, the existence of the square root

can be seen

as follows:

and

From Theorem 6.4.2, it follows that

exists.

6.5.2. A New Look at Dirac’s d Function

We show that, as a real-valued function is a function from a subset of I

(0)

to a

subset of I

(0)

Dirac’s δ function can be considered as a function from GNS into

GNS

. Therefore, it is a more natural representation. At the same time, the integral

convenience, boldfaced letters will be used for

GNS

-related concepts and lightface

letters for real-valued concepts. For example, f(x) is a real-valued function, and

(

) is a function from a subset of GNS to a subset of GNS.

Without loss of generality, let y = f

(

) be a function from GNS to GNS. We

define the integral of the function inductively as follows.

Let E = {x

∈ GNS : f

(

)

≠

Case 1: Suppose that for each x ∈ E, x

–m

= 0 for all

∈ the set of all

natural numbers, and that y = (… , y

–m

, … ,y0, … ,y

, … ), where, in general,

= y

(

) is a function of all x

∈

{0}.

Step 1: Define a subset H

(0)

⊆

as follows:

∈ H

(0)

iff

–n

= 0 if n > 0

and

= y

(

) a function of

(6.11)