Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

132

Chapter 6

and let

(6.12)

If the real-valued

function f

(0)

is Lebesgue integrable on

then

–

(0)

has

Lebesgue measure zero, denoted

Step n: Assume the real numbers

have all been defined.

For fixed

define a subset H

)

⊆

as follows: x

∈

)

iff

–m

= 0 if m > n and y

–n

= y

–n

) a function of x

(6.13)

and let

(6.14)

If the real-valued function

is Lebesgue integrable on denote the

integral on

is meaningful

— that is, if there are only up to countably many nonzero summands and the

summation is absolutely convergent—then the sum is denoted a

)

Definition 6.5.1

[Wang (1985)].

function

(

is convergent and equals

, then the

) is GNL-integrable and we write

Case 2: Partition the set E as follows:

where

= {x ∈ GNS : k(

) = – k}. Consider the right-shifting of

, and the left-shifting of f(

Using the method developed in Case 1, denote

Definition 6.5.2 [Wang (1985)]. If

∑

is convergent, then the function f(

) is

GNL-integrable and we write

A Mathematics of Computability that Speaks the Language of Levels

133

We are now ready to look at Dirac’s δ function. Let ƒ:

be infinitely

differentiable and define

f : GNS

→

GNS

as follows:

This function is called the GNS function induced by ƒ(

). Then it can be shown

that 6.5.1 holds.

Theorem 6.5.1 [Wang (1985)]. Let ƒ and f be defined as before. Then there is a

GNL

-integrable function

GNS → GNS such that

In particular, let

be arbitrary and infinitely differentiable with bounded

support: that is,

Sup(

g) = {x ∈

(

)

≠ 0

}

is bounded in

and

(

)

Then the

GNL

-integrable function

GNS → GNS can be defined

,...)

otherwise

if x = (... ,

That is, g

(

) is a Dirac δ function according to Eq. (6.2).

Proof: Pick a real-valued function g: such that g is infinitely differ-

entiable with bounded support and satisfies

Define

for x

= ( . . . , 0,

, ...)

otherwise

Then

for x = (..., 0, x

, ...)

otherwise

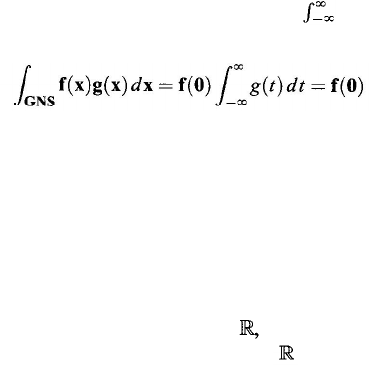
134

Chapter 6

Since

(f)(x

)

(

))

– n

= 0, for each n = 0,1,2, ..., and g(

)

dt = 1, it follows

that

This

completes

the proof.



For a more rigorous treatment of GNS, please refer to Chapter 11

6.6. Some Final Words

If the ordered field GNS is substituted for we can see that the theory and

applications of GNS will have a great future, since has been applied in almost

all areas of human knowledge and been challenged numerous times. As shown

in (Wang, 1985; Wang, 1991), many studies can be carried out along the lines

of classical research, such as mathematical analysis, distribution theory, quantum

mechanics, etc., on GNS. Not only this, we also expect that when one is studying

topics from various disciplines with GNS, some open problems in relevant fields

might be answered, and some new fields of research might be opened up. Most

importantly, we hope that the study of GNS will furnish a convenient tool for a

computational general systems theory.

CHAPTER 7

Bellman’s Principle of Optimality and

Its Generalizations

In dynamic programming Bellman’s principle of optimality is extremely important.

The principle says (Bellman, 1957) that each subpolicy of an optimum policy must

itself be an optimum policy with regard to the initial and the terminal states of the

subpolicy. Here, the terms “policy,” “subpolicy,” “optimum policy,” and “state”

are are primitive and are not given specific meanings. In each application, these

terms are understood in certain ways comparable to the situation of interest. For

example, in a weighted graph, an optimum path from a vertex v

to vertex v

the one with the smallest sum of weights of the edges along the path. In this case,

a “policy” means a path, a “subpolicy” a subpath, an “optimum policy” stands

for a path with the smallest weight, and “the initial and terminal states” for the

beginning and ending vertices v

and v

respectively. The principle implies that

for each chosen optimum path from v

to v

each subpath must be an optimum

path connecting the initial and terminal vertices of the subpath.

7.1. A Brief Historical Note

During the last half century or so, Bellman’s principle has become the cor-

nerstone in the study of the shortest-path problem, inventory problem, traveling-

salesman problem, equipment-replacement models, the resource allocation prob-

lems, etc. For details see Dreyfus and Law (1977). However, since the early

1970s, a number of practical optimization problems have been put forward in

management science, economics, and many other fields. One feature common

to all these problems is that the performance criteria are not real numbers, and

consequently, the optimum options are no longer maxima or minima of some

set of real numbers. Many dynamic programming models with nonscalar-valued

performance criteria have been established. See (Bellman and Zadeh, 1970; Mit-

ten, 1974; Wu, 1980; Wu, 1981a; Furukawa, 1980; Henig, 1983; Baldwin and

Pilsworth, 1982).

135

136

Chapter 7

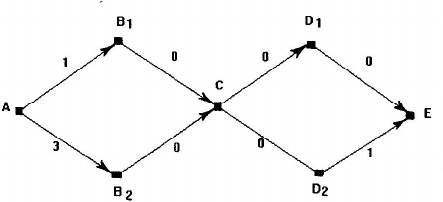
Figure 7.1. A subpolicy of the optimum policy is no longer optimum.

Since the application of Bellman’s principle is no longer restricted to classical

cases, scholars began to question how far the validity of the principle can be

carried. Hu (1982) constructed an example to show that the principle does not

hold in general. In fact, it was shown by Qin (1991), that if the goal set is strong

antisymmetric, then the sum of local optimization orders is less than or equal to

the global optimization order. Therefore, the following natural question arises.

Question 7.1.1 [Hu (1982)]. Under what characterizations can a given problem

be solved by dynamic programming?

At the same time, as many scholars have realized, it is the fundamental equation

approach, not the principle of optimality, that makes up the theoretical foundation

of dynamic programming. The optimum principle gives one a property of the

optimum policy, while the fundamental equation approach offers one an effective

method to obtain the desired optimal policy. Since the validity of Bellman’s

principle is limited, is the fundamental equation approach also limited? Again,

Hu’s counterexample shows that the fundamental equation approach does not

always work. Thus, the following questions are natural:

Question 7.1.2 [Wu and Wu (1986)]. In what range does the fundamental equa-

tion approach hold? How can its validity be proved? What relations are there,

if any, between the fundamental equation approach and Bellman’s Principle of

Optimality?

To seek the answer to these questions, several approaches of systems analysis

presented.

are

7.2. Hu’s Counterexample and Analysis

Let us first look at Hu’s counterexample.

Bellman’s Principle of Optimality and Its Generalizations

137

Example 7.2.1. Consider the network in Fig. 7.1. Define an optimum path as

one where the sum of all arc lengths (mod4) is the minimum. Then the policy

→ B

→

is optimum, but its subpolicy

→ C →

→ E is not

optimum, since B

2 → C →

→

is, which has weight 0.

Now let W ={0,1,2,3 ,...

} be the set of all possible weights,

= minimum:

(

W) → W be the optimum option, which is a mapping from the power set p(W

)

of W, the set of all subsets of W, into W such that

(7.1)

and let

= {+}

(mod4) :

² → W be the binary relation on W such that

(7.2)

where

stands for the ordinary composition of mappings.

If G is a nonempty set, representing the set of all vertices, then each network

or graph or weighted graph is simply an element g

∈

↑

where W ↑ G² is

the set of all mappings from G² =

× G into W. For any

∈

define

where

Then Bellman’s principle of optimality can be written as follows.

Theorem 7.2.1 [Bellman’s Principle of Optimality].

For any natural number

n, elements

(7.3)

where z is the zero in W, then for any

≤ i ≤

≤ n,

For any

∈ W ↑ G²

, a natural number n, and a, b

∈ G, the fundamental

equation on (

; n , a, b

) is given by the following functional equations:

where

≤ m ≤ n.

Applying these equations to Hu’s counterexample, one obtains:

〈

〉

(

A,E

) =1, with

A →

→ C → D

→

being its policy. However, it can be

easily seen that

〈4

〉

(

)

= 0 and A → B

→

is the global optimum

policy with weight 0. That is, in this example,

〈

〉

(

A,E

)

≠

〈

(

〉

A,E

Hence, we

ask when will the weight obtained from the fundamental equation approach be the

same as the global optimum weight?

138

Chapter 7

7.3.

Generalized Principle of Optimality

By formalizing the discussion in the previous section, Wu and Wu (1984a)

obtained one sufficient and three necessary conditions for Bellman’s principle to

hold. In this section, all results are based on (Wu and Wu, 1984a).

In general, let W and G represent two nonempty sets,

(

)

→ W be the

optimum option satisfying Eq. (7.1), and

be a mapping from W

into W. For

any element g

∈ W ↑ G

and any

∈ G, define

where

An element z

∈ W is called a zero element, or simply zero if

for each

∈

and

for each

The optimum option

is X-optimum-preserving for X ∈ p(W) if

for any

The option

satisfies the optimum-preserving law if

is X-optimum-preserving

for all

The relation θ

is distributive over θ

for all

≠

∈

(W ) and any x ∈ W, and

for all

≠ X ∈ p (W ) and x ∈ W. The relation θ

is associative if for any

∈ W,

The relation θ

satisfies the cancellation law if for any w

, w

∈ W,

implies w

and

implies w

= w

whenever w

is not the zero element in W.

Bellman’s Principle of Optimality and Its Generalizations

139

Theorem 7.3.1 [Generalized Principle of Optimality (Wu and Wu, 1984a)].

Assume that

satisfies the optimum-preserving law and that θ

is associative,

cancellative and distributive over

. Then in the system (

W, G;

, θ

Bellman's

Principle of Optimality (Theorem 7.2.1) holds.

Proof:

Suppose that g ∈ W ↑ G

, n is a natural number,

and

For any 0 ≤ i ≤ j ≤ n, since

and

then by the optimum-preserving law of

, it follows that

By the associative law and the distributive law over θ

, one has

Since

one has that

ω(a

...

)

≠ z and ω

j +1

...

) ≠ z.

Therefore, by the cancellation law of

That is,

The generalized principle of optimality is a sufficient condition of the con-

servation from a global optimization to local ones. In the following section, it is

shown that the conditions in the generalized optimality principle are also necessary

except for the condition of associativity.

140

Chapter 7

7.4.

Some Partial Answers and a Conjecture

Theorem 7.4.1 [Wu and Wu (1984a)]. Assume that θ

is associative, n a natu-

ral number, and a

, a

, . . . , a

∈ G satisfy Eq. (7.3). If the Generalized Principle

of Optimality (Theorem 7.3.1) holds for a chosen g

∈ W ↑ G

, then θ

pos-

sesses the following property of cancellation: for any 0

≤ i < j < k ≤ n and any

(7.4)

implies

and

implies

Proof: Since

and from the assumption

that the Generalized Principle of Optimality holds, it follows that

(7.5)

By Eq. (7.4) and the associative law of

, it follows that

That is,

From the assumption that the Generalized Principle of Optimality holds, it

follows that

(7.6)

Bellman’s Principle of Optimality and Its Generalizations

141

By Eqs. (7.5) and (7.6), it follows that

The proof of the other equation is similar and is omitted.

Theorem 7.4.2 [Wu and Wu (1984a)]. Assume that

satisfies the optimum-

preserving law,

is associative, n os a natural number, and a

, a

, . . . , a

∈ G

satisfy Eq. (7.3). If the Generalized Principle of Optimality (Theorem 7.3.1) holds,

then θ

possesses the following distributivity over θ

: for 1 ≤

i ≤ n – 1,

and

Proof: Since it is assumed that the Generalized Principle of Optimality holds,

it follows that

(7.7)

The assumption that

satisfies the optimum-preserving law implies that

(7.8)

Then, from Eqs. (7.7) and (7.8) and the associative law of

, it follows that

just what is desired. The proof of the other identity is similar and is omitted.