Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

142

Chapter 7

Theorem 7.4.3 [Wu and Wu (1984a)].

Assume that

is associative and distribu-

tive over θ

and n is a natural number, and a

, a

, . . . , a

∈ G satisfy Eq. (7.3). If

the Generalized Principle of Optimality (Theorem 7.3.1) holds, then

possesses

the following optimum-preserving property: for each 1

≤ i ≤ n – 1,

Proof: Since the Generalized Principle of Optimality is assumed to be true,

Therefore, by associativity and the distributive law over

of θ

, it follows that

The proof of the other identity is similar and is omitted.

We conclude with the following conjecture.

Conjecture 7.4.1. In the system (

W, G;

), the Generalized Principle of Op-

timality holds iff there is an ordering relation

≤ on W such that

(i)

for any x, y ∈ W, one and only one of the following must be true:

(ii)

the optimum option θ

is defined by θ

= superior or θ

= inferior under

the ordering relation

≤

(iii)

the ordering relation ≤ and the relation θ

are consistent. That is, x ≤ y iff

w ≤ y θ

w and w

x ≤ w θ

y for any w ∈ W.

Bellman’s Principle of Optimality and Its Generalizations

143

7.5. Generalization of Fundamental Equations

In the previous two sections, Bellman’s Principle of Optimality has been

generalized and three necessary conditions given. However, one should keep in

mind that the optimum principle only states a property of the optimum policy, while

the fundamental equation approach offers an effective method for one to obtain

the desired optimal policy. In this section, a sufficient condition and two necessary

conditions are established under which the fundamental equation approach holds.

That is, under the conditions, the weight computed from the fundamental equation

equals that of a global optimum. The presentation here is based on Shouzhi Wu

and Xuemou Wu (1986).

For a given system (

W, G; θ

), defined in the same way as in the previous

section, for any g

∈ W ↑ G

, a natural number n, and a, b ∈ G, the following

functional equations are called a fundamental equation on (

; n, a, b), or simply a

fundamental equation:

(7.9)

for 2

≤

Here, the mappings

and

express the recursiveness of operation,

which in turn shows that Eq. (7.9) is a generalization of the fundamental equations

in dynamic programming (Bellman, 1957).

Theorem 7.5.1 [Wu and Wu (1986)].

In the system

(

W, G; θ

, θ

), if θ

satisfies

the optimum-preserving law, and

the associative and distributive laws over θ

then for any

and a

, b ∈ G

the following is true:

Proof: For any and a, b ∈ G

, mathematical induction will

be used on the index m to show that

When m =

1, it is obvious that

Suppose that

for some and any a and b

∈ G. It

is now sufficient to show that

Since

satisfies the

associative and distributive laws, for any

∈

, one has

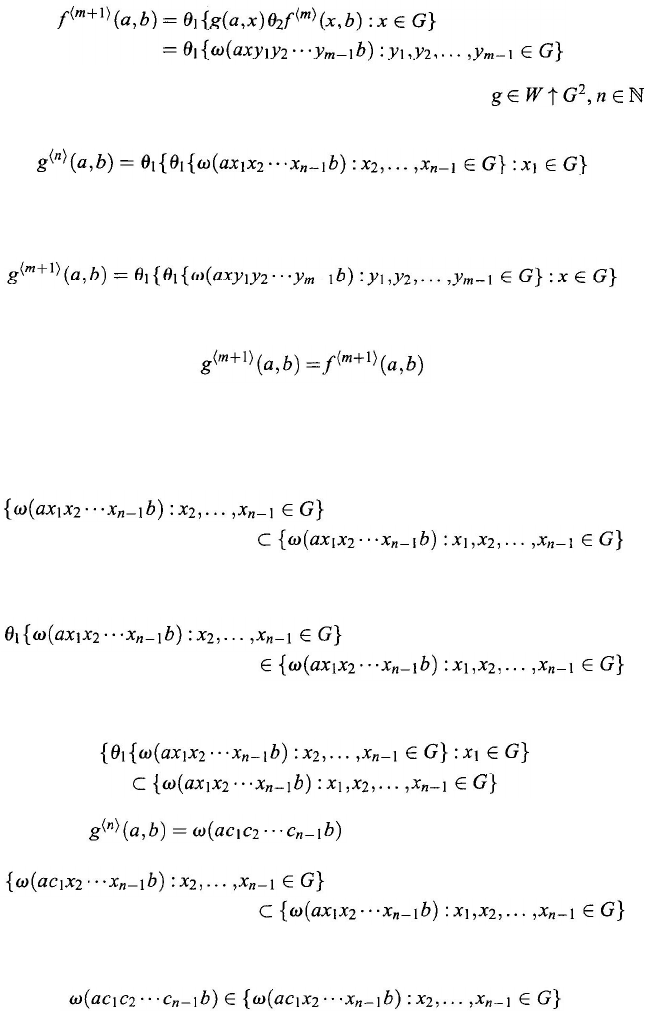
144

Chapter 7

Therefore,

Claim.

satisfies the optimum-preserving law, then for any

and

∈

the following equation holds:

satisfies the

optimum-preserving

law and the Claim

Now the assumption that

guarantee that

Thus,

which is what we desired.

To finish the proof of the theorem, let us see why the claim is true.

Proof of claim: First note that for any x

∈ G

, the following is true:

Therefore, for any x

∈

, one has

Hence, it follows that

(7.10)

Assume that for some c

, . . .

n–1

∈

Since

and

Bellman’s Principle of Optimality and Its Generalizations

145

and

satisfies the optimum-preserving law, it follows that

This equation implies at once that

(7.11)

Now, Eqs. (7.10) and (7.11) and the assumption that θ

satisfies the optimum-

preserving law imply that

This ends the proof of the theorem.

The following results show that the conditions in Theorem 7.5.1 are also

necessary.

Theorem 7.5.2 [Wu and Wu (1986)].

In the system

(

, G; θ

, θ

) with θ

satis-

fying the optimum-preserving law and

satisfying the associative law, if for any

and a

, b ∈ G, it is true that

then

possesses the following distribution over

: for any g

and a

∈

Proof: For any and a, b ∈ G

, and since

satisfies the

optimum-preserving law, from the Claim it follows that

From the assumption that

satisfies the associative law, it follows that

Therefore,

(7.12)

146

Chapter 7

Now, from the assumption that for any and a, b ∈ G, the

following is true:

Thus,

(7.13)

By Eqs. (7.12) and (7.13), it finally follows that

This ends the proof of the theorem.

Theorem 7.5.3 [Wu and Wu (1986)].

In the system

(

W, G; θ

) with θ

satis-

fying the associative law and the distributive law over

, if for any g

∈

↑

and a

, b ∈ G, it is true that

then

possesses the following optimum-preserving property: for any g ∈ W ↑

and a and b ∈ G, the following is true:

Proof:

Since for any and

a, b

∈

, it is true that

and

satisfies the associative law and the distributive law over θ

, it

then follows that

as desired.

Bellman’s Principle of Optimality and Its Generalizations

147

7.6. Operation Epitome Principle

Define a mapping

so that the following conditions are satis-

fied:

This section presents a different approach to systems analysis, which is due to

Qin (1991). With this approach, Bellman’s Principle of Optimality once again is

generalized. The generalized result is called the “operation epitome principle.”

For an N-stage sequential decision process, let X

be the set of all states of

the ith stage,

= 0, 1, 2, . . . ,

, where

, X

,. . . , X

are some fixed sets.

Let

and define

a binary relation g

⊆

by the following: for any x

y ∈ W

, (x

y) ∈ g iff x ≤ y.

Further,

→ W is the gain (function) of decisions. Intuitively speaking,

the set

consists of all available policies, and the set

is made up of all the criteria

used in the decision-making process. The binary relation g ⊆ W

establishes the

comparison between criteria.

(1) F(

= w for each w

∈ W.

(2) For each (

, w

, . .

. ,w

)

∈

, i ≤ N, and 1 ≤ k ≤ i,

(3) For each fixed w

∈ W, the mappings F

(

) and F

(

·) : W → W are

strictly order-preserving. That is, for any x

∈

, x < y iff

(

x, w) <

(

y, w), and x < y iff

(

x) < F (

For example, it can be shown that the addition operation of real numbers can

be the mapping F. In addition, if W contains all positive real numbers, then the

multiplication operation can also be the mapping F.

The gain of the policy

1–

= (

, . . . ,

)

∈

is measured by the function

ƒ : E → W

, defined by

For a subpolicy

with initial state

∈

and terminal state x

∈

, the gain of e

i –j

is defined as follows:

and

148

Chapter 7

Now, for each policy

∈

, the stationary set (of the policy e) is defined

Theorem 7.6.1 [Bellman’s Principle of Optimality].

For any policy e

1–N

(

, e

, . . . ,

)

∈

E, if the equation

STY(

–N

)

holds in the system (

;ƒ,g

then for any natural numbers i and j satisfying 0

≤ i ≤ j ≤ N, the subpolicy

i–j

(

, e

i +1

, . . . , e

) of the policy e

1 –N

satisfies the condition that the equation

STY(

i–j

) = holds in the system (W, E

i–j

;

If STY(

) = , then ƒ

(

) is called a generalized extreme value of ƒ

(

). Then,

Bellman’s Principle of Optimality can be written as follows.

To prove this new version of Bellman’s principle, we first formalize the previous

discussion.

Consider the system (W, E;ƒ, g) such that E and W are nonempty sets, ƒ :

→ W is a mapping and g ⊆ W

is a binary relation. This system is called the

optimization model of the general systems. The set W consists of all the criteria

used in an optimization problem of interest, and

is the set of all possible policies.

These sets are called the criteria set and the policy set of (

, E : ƒ, g

), respectively.

Intuitively speaking, for each chosen criterion

∈

, there exists exactly one policy

w ∈ W and the rule matching the criterion e with the policy w is described by the

function ƒ : E

→ W. The binary relation g ⊆ W

defines how to compare criteria

used.

For any subset X ⊆ W, define

If X = ƒ

(

) and w ∈ X – g * X, then there exists at least one x ∈ X = ƒ

(

) such

that x

≠ w and (

) ∈ g.

Let e

∈ E be such that w = ƒ

(

e) ∈ ƒ

(

E) – g * ƒ(E).

Then the element w

∈ W is called a generalized extreme value of the set X = ƒ(E),

and the element e

∈ E is a generalized optimal solution (or policy) of the model

;

= {

w ∈ X : for anyx ∈ X, x ≠ w implies (w, x) ∉ g

}

Lemma 7.6.1 [Qin (1991)]. If X ⊆ W is a nonempty subset, then

where I is the diagonal of the Cartesian product X

defined by I

= {(

x, x) : x ∈ X

Proof: For each element w ∈ g * X, by the definition of g * X it follows that,

for any x

∈ X, if x ≠ w, then (w, x) ∉ g. That is, w ∈ X and w ∈ (g

)(

) =

(7.14)

Bellman’s Principle of Optimality and Its Generalizations

149

and x ≠ w, then x ∈ g

(

w). That is, (W, x

)

∈

contradiction. So,

This proves that

Conversely, if for

then for any

∈

≠

must

imply (

x) ∉ g

, since otherwise,

which is impossib1e.

Now, for each policy e ∈ E the stationary set (of the policy e) is defined

If STY(

) = , then ƒ

(

) is called a generalized extreme value of ƒ

(

); that is,

(e) ∈ g * ƒ(E).

A mapping F : X

→ W, where X ⊂ W

, is called strictly order-preserving if the

following property holds: for any x

y ∈ X

(

x) ≠ F

(

y), (

(

y)) ∈ g if and only if x ≠ y, (x

y) ∈ g

Theorem 7.6.2 [Operation Epitome Principle (Qin, 1991)]. Let W and E =

× E

be nonempty sets, g ⊆ E

a binary relation, and h

: E

→ W, i = 1,2,

mappings. If a mapping satisfies

(i)

(

w) = w, for each w ∈ W.

(ii)

For each fixed w, the mappings F

(

w,·

) and F

(

·, w) : W → W are strictly

order-preserving, then a mapping

can be defined by

and

i = 1, 2

for each e = (e

, e

) ∈ E such that

where

⏐

is the cardinality of the set X.

Proof: For any e' ∈ E

, define the mapping p

: E

→ E, which depends on

fixed

, by

(

) = (

,e'

) for each

∈

For any e' ∈ E

define the mapping

: E

→ E

, which depends on fixed

, by

(

) = (

)

for each

∈

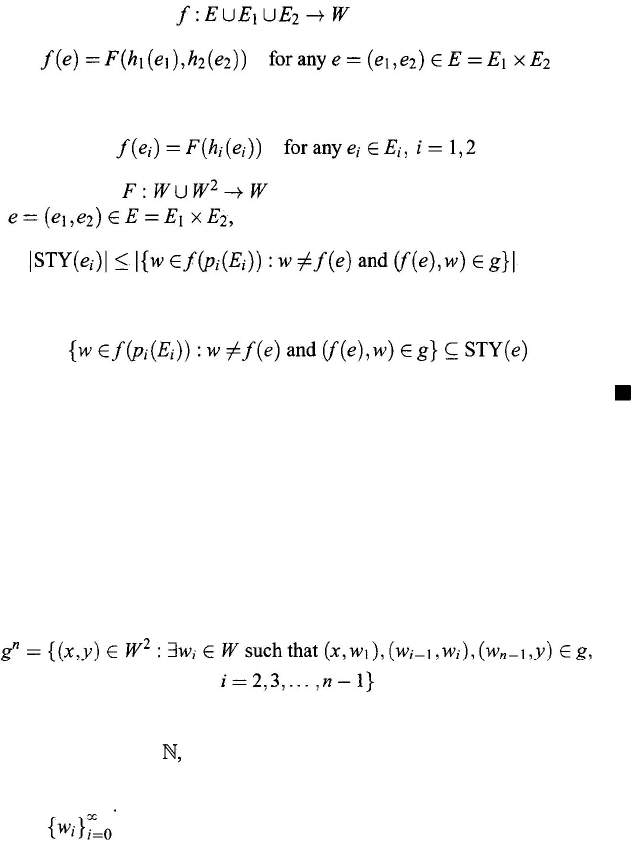
150

Chapter 7

Now the desired mapping

is induced by

and

Since the mapping is strictly order-preserving, one has that, for

each

(7.15)

On the other hand, it is easy to see that

(7.16)

Equations (7.15) and (7.16) imply the desired inequality.

Now, Bellman’s Principle of Optimality (Theorem 7.6.1) is clear.

7.7. Fundamental Equations of Generalized Systems

For an optimization model (

W, E

;

, g

) of general systems and a natural number

n ∈ N, the relation g

⊆ W

is defined

A binary relation g ⊆ W

is strongly antisymmetric (Qin, 1991), if for any

natural numbers m, n

∈ there do not exist distinct elements x

y ∈ W such that

the conditions (x,y)

∈ g

and (y

x) ∈ g

hold simultaneously. A binary relation

g ⊆ W

is strictly strongly antisymmetric (Qin, 1991), if there is no infinite

sequence

such

that

≠

and

(

i+1

)

∈

for each

= 0, 1, 2, . . .

It can be seen that the concept of strong antisymmetry is a generalization of

the concept of partial ordering relations. To this end, recall that a relation g

⊆ W

is called a partial ordering (Kuratowski and Mostowski, 1976), if the following

conditions are satisfied:

(i) (Antireflexivity) (

x) ∉ g for any x ∈ W.

(ii) (Antisymmetry) If (

y) ∈ g and x ≠ y, then (y

x) ∉ g for x

∈

(iii) (Transitivity) If (x

y) and (y

z) ∈ g, then (x

z) ∈ g for x

∈

Bellman’s Principle of Optimality and Its Generalizations

151

First, if a relation g ⊆ W

is a partial ordering, g must be strongly antisymmetric.

Suppose that this statement is not true. That is, the relation g

⊆ W

is a partial

ordering but not a strongly antisymmetric relation. Hence, there exist

∈ W

such that w

≠ w

, and natural numbers m, n ∈ such that and

From the transitivity of

, it follows that

and w

≠ w

. This last condition contradicts the antisymmetry of g. Second, the

following example shows that a strongly antisymmetric relation g

⊆ W

may not

be a partial ordering relation.

Example 7.7.1. Let W = and for any a, b

∈ W, (

, b) ∈ g ⊆ W

, iff b + 1 >

a > b. It can be shown that (

)

∈

, for

∈

iff b + m ≥ b + 1 > a > b ;

and that (

)

∈

, for n ∈ iff a + m ≥ a + 1 > b > a. Therefore, g is strongly

antisymmetric.

However, it is not a partial ordering relation on W, since the

transitivity relation is not satisfied.

Theorem 7.7.1 [Qin (1991)]. If a set W is finite, then a binary relation g

⊆ W

is strictly strongly antisymmetric iff the relation g is strongly antisymmetric.

Proof: Necessity. Suppose that g

⊆ W

is strictly strongly antisymmetric but

not strongly antisymmetric. From the definition of strong antisymmetry it follows

that there exist w

, w

∈ W and m

∈

such that

and

Thus, there exist elements w

, i = 1, . . . , m – 1, and w

= 1, 2 , . . . ,

– 1, such that

and

That is, there exists a finite sequence

such that

≠ x

i +1

, for i = 1, 2 , . . . , m + n–1 and (x

i +1

) ∈ g, for i =1, 2, . . . , m + n–1

Now an infinite sequence can be defined as follows:

and

It is easy to observe that y

≠ y

i +1

and (y

i +1

) ∈ g for each i ∈

which

contradicts the assumption that g is strictly strongly antisymmetric.

Sufficiency. Suppose W is finite and g

⊆ W

is strongly antisymmetric. As-

sume that g

⊆ W

is not strictly strongly antisymmetric. There then exists an

infinite sequence

such that y

i -1

≠ y

and (y

i –1

, y

)

∈

for each

∈