Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.

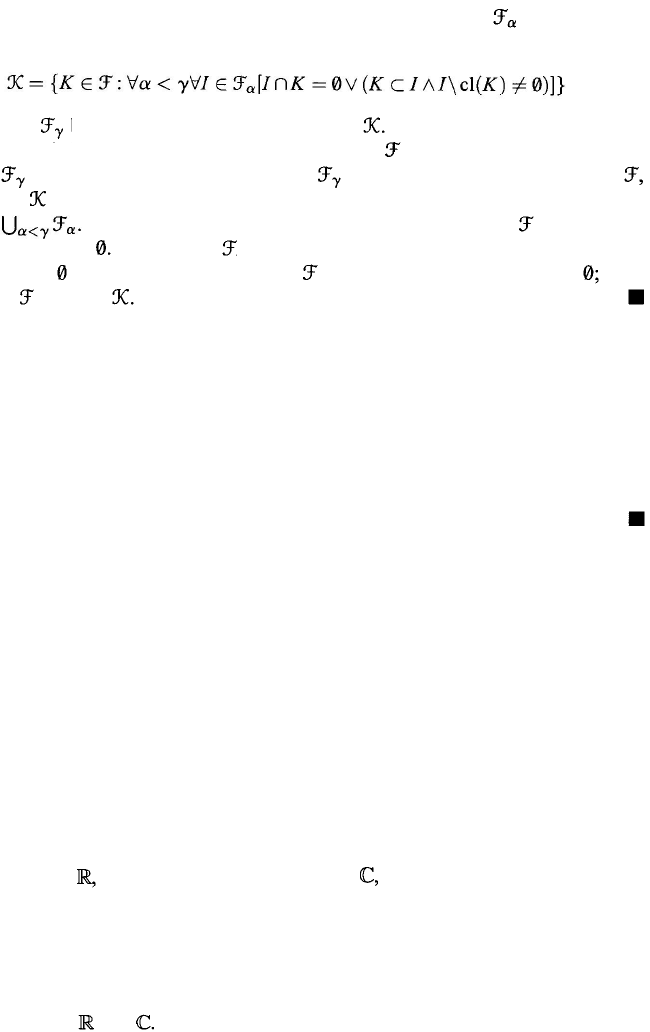
90
Chapter 3
Finally, we assume γ is a limit ordinal and have defined the for each α < γ
satisfying (1)–(3) for α < β < γ. Let
and let
be a maximal disjoint subfamily of
Then (1) and (3) now hold for
all
α < β < γ. For β = γ, (2) says that no J ∈ is disjoint from all members
of
; this will follow by maximality of ιφ we can show that for each J∈
∃
K ∈
(
K ⊂ J). Let E be the set of all left and right endpoints of all intervals
in
E is countable and J is not separable, so fix K
1
∈ with K
1
⊂ J
and K
1
∩
E
=
If I ∈
∪
α<γ
α, thenK
1
does not contain the endpoints of I, so
I
∩
K
1
=or K
1
⊂ I. Now take K ∈ with K ⊂ K
1
and K
1
\cl(
K ) ≠ then
K
⊂
and
K
∈
(3.64)
Theorem 3.3.15. MA
(
ω
1
) implies that there are no ω
1
-Suslin trees.
Proof:
Let (
T
, ≤) be an ω
1
-Suslin tree, and let P = (T, ≥), the reverse order
of T. Since T has no uncountable antichains, P has ccc. By Theorem 3.3.12, we
may assume that T is well-pruned, in which case D
α
= {
x ∈ T : ht(x, T) > α} is
dense in P. By
ΜΑ(
ω
1
), there is a filter G intersecting each D
α
. Then G is an
uncountable chain, contradicting the fact that T is a Suslin tree.
First question: Is there anything which is not a set? We have declared that
our axioms of set theory deal with sets
— in fact, hereditary sets (Section 3.1).
Furthermore, the Axiom of Extensionality has embodied in it the assertion that all
things in our domain of discourse are sets. It seems likely that we have not left any
interesting mathematics behind by so restricting our universe, since mathematical
objects like the set of all real numbers, and the set of all complex numbers,
are hereditary sets and have been defined explicitly within this domain in Section
3.2.
Second question: Is there an “object” x such that x = {x}? This question is
independent of the existence of physical reality, and such a set x would clearly be an
hereditary set. Such an object x did not occur in the construction of mathematical
objects like
and
This is also an important question in systems theory (see
Chapters 8 and 12).
Some questions about sets are relevant to applications of mathematics. We
give two of the most important questions. A detailed discussion on the relevance
between the questions and applications of mathematics will be given in Chapter 8.
3.4. Well-Founded Sets
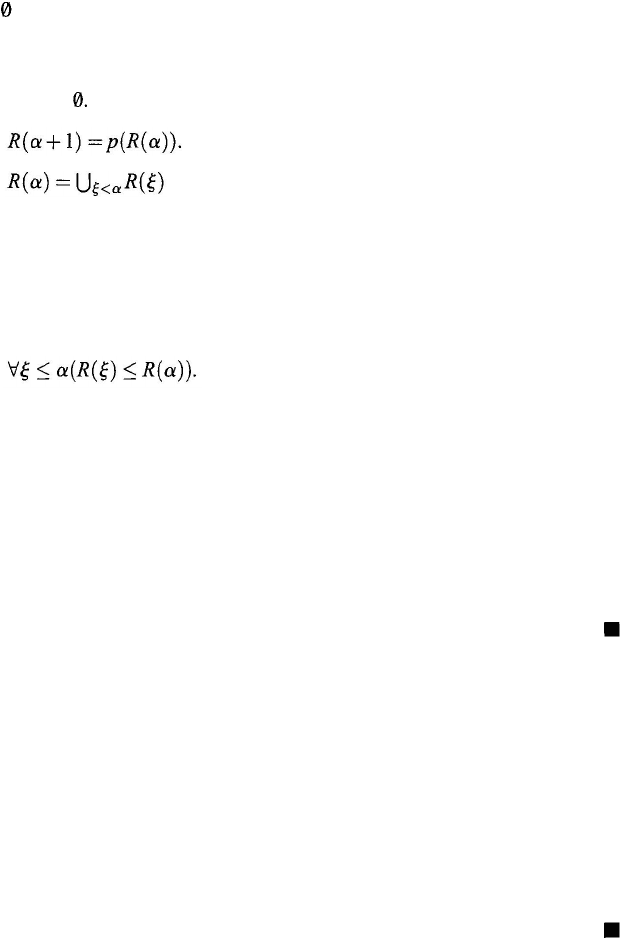
Axiomatic Set Theory
91
In this section, we study the position of the Axiom of Regularity relative to
the axioms in axiomatic set theory. We work in the axiom system of all axioms in
ZFC except Regularity and define the class WF of well-founded sets by starting
with and iterating the power set operation. Then we show that WF is closed
under the other set-theoretic operations as well.
Let us define R (
α
) for each
α ∈
ON
by transfinite recursion as follows:
(a) R
(0) =
(b)
(c)
when
α is a limit ordinal.
A set A is well-founded if there is an
α ∈ ON such that A ∈ R(
α
). Let WF be the
class of all well-founded sets, i.e., WF =
∪
{
R
(
α
) : α ∈ ON
}.
Theorem 3.4.1. For each ordinal α:
(a) R
(
α
) is transitive.
(b)
Proof:
We use transfinite induction on
α
: We assume that the result holds for
all
β < α and prove it for α.
Case 1.
α = 0. the result is trivial.
Case 2.
α is a limit. Statement (b) is immediate from the definition; (a)
follows from the fact that the union of transitive sets is transitive.
Case 3.
α = β +1. Since R
(
β
) is transitive, p
(
R
(
β
)) = R
(
α
) is transitive and
R
(
β
) ⊂ R
(
α
).
Th
is
establishes (a) and (b) for all ordinals
α
.
Let x ∈ WF, the least ordinal α with x ∈ R(
α
) must be a successor ordinal.
The rank of
x,
denoted by rank(
x), is the least β such that x ∈ R (β + 1). Hence,
if
β = rank(x), then x ⊂ R
(
b
),
and x ∉ R
(
β
), and x ∉ R
(
α
) for all α > β.
Theorem 3.4.2. For each ordinal
α
,
R
(
α
) = {
x
∈
WF
: rank (
x ) < α
}
Proof:
For
x
∈
WF
, rank
(
x
) < α if and only if ∃β < α
(
x ∈ R
(
β + 1)) if and
only if x
∈ R(
α
).

92
Chapter 3
Theorem 3.4.3. If y ∈ WF, then
(b) rank(
y
) =
∪
{rank(
x ) + 1 : x ∈ y}.
(a)
∀x ∈ y
(
x ∈ WF ∧ rank(x) < rank(y
)).
Proof: For (a), let α = rank(
y
), then y ∈ R (α + 1) = p (
R
(
α
)). If x ∈ y ,
x
∈
R
(
α
), so rank(x) < α.
For (b), let
α = ∪
{rank(
x
) + 1 : x
∈ y}. By (a) α ≤ rank(y). Furthermore,
each x
∈ y has rank < α, so y ⊂ R
(
α). Thus, y ∈ R
(
α +l), so rank(y) ≤ α.
Theorem 3.4.3 says that the class
WF
is transitive and that we may think of the
elements
y
∈
WF
as being constructed, by transfinite recursion, from well-founded
sets of smaller rank. Therefore, the class
WF
excludes sets which are built up from
themselves. More formally, there is no x ∈ WF such that x ∈ x, since from this
we would have rank(x) < rank(x). Likewise, the class WF excludes circularities
like
x
∈
y
∧
y
∈
x
, since this would yield rank(x) < rank(y ) < rank(x). It is clear
that the following result holds.
Theorem 3.4.4. Each ordinal is in WF and its rank is itself.
Proof: What we need to show is that
∀α ∈ ON
(
α ∈
WF
∧
rank(
α) = α ). We
prove this by transfinite induction on
α. Assume that the theorem holds for all
β < α. Then, for β < α, β ∈ R
(
β
+ 1) ⊂ R(
α
), so α ⊂ R
(
α
), so α ∈ R
(
α
+1).
By Theorem 3.4.3(b), rank(
α
) = ∪
{
β + 1 : β < α} = α. Thus the theorem holds
for all ordinals
α.
Theorem 3.4.5.
∀α ∈ ON
(
R
(
α
)
∩
ON
=
α
).
The proof follows from Theorems 3.4.4 and 3.4.2.
Theorem 3.4.6.
(a)
If x
,
y
∈
WF
, then x
×
y, x
∪
y, x
∩
y,
{
x
,
y
}
, and y are all in WF, and the
rank of each of these sets is less than max{rank(x), rank(y)} +
ω
.
If x
∈ WF, then ∪x, p
(
x
)
, and {x
}
∈
WF
, and the rank of these sets is less
than rank(x) +
ω.
(b)
x
Proof: For (a), let α = rank(
x
). Then x ⊂ R
(
α
), so p (x) ⊂ p (R
(
α
)) =
R
(
α + l), so p
(
x) ∈ R
(
α + 2). Similarly, {x
}
∈
R
(
α + 2) and ∪x ∈ R(
α
+ 1).
For (b), let α = max{rank(x
), rank(
y
)}. As in (a), we show, e.g., {x, y}
∈
R
(
α
+2),(x
,
y
)
∈ R
(
α +3). Any ordered pair of elements of x ∪ y is in R
(
α
+ 3),
so
y
x
⊂
R
(
α
+ 3), so
y
x
∈
R
(
α
+ 4). We leave the rest of the details for the reader.
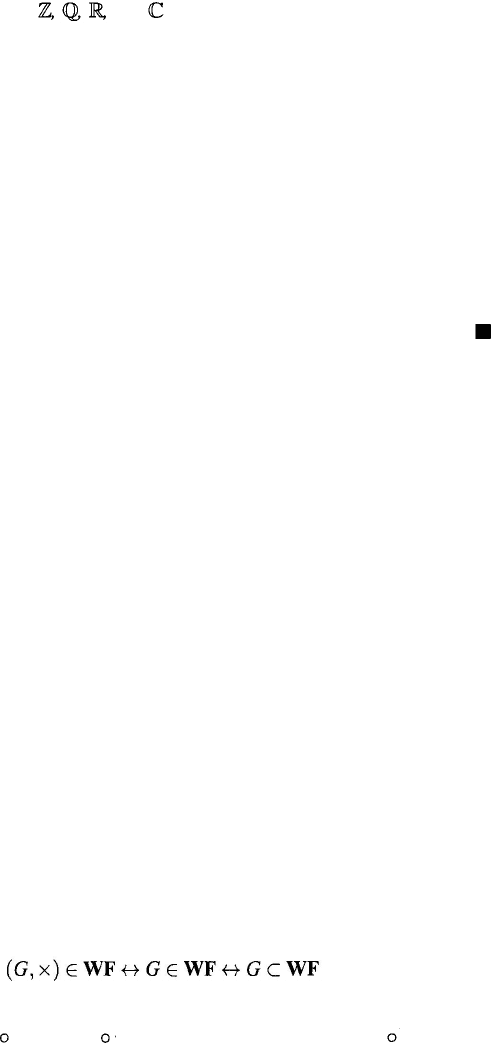
Axiomatic Set Theory 93
Theorem 3.4.7.
The sets
and
are all in R
(
ω + ω).
The proof follows from Theorem 3.4.6 and the definitions of these sets in
Section 3.2.
Theorem 3.4.8.
(a)
∀
n
∈ ω
(|
R(
n
)| < ω).
(b)
|
R
(
ω
)|=
ω
.
Proof:
(a) is easy by induction on
n.
For (b), since
ω ⊂
R
(ω
), it is sufficient to
see that R
(
ω) is countable. To show this by induction, for each n we may identify
R
(
n + 1) with
R
(
n
)
2 and order it lexicographically. Then the ordered sum of the
sets R
(
n
), n ∈ ω, has order type ω.
The cardinalities of the sets R(
α) increase exponentially: |R(
ω
)| = ω
,
|R
(
ω
+ 1)| = 2
ω
, |R
(
ω + 2)| = 2
2
ω
, etc. Generally, let a
α
be defined by trans-
finite recursion on
α as follows:
(1) a
0
= ω
.
(2) a
α +1
= 2
a
α
.
(3) For a limit
γ
,
a
γ
=
∪
{
a
α
: α < γ }.
Then we have the following theorem.
Theorem 3.4.9. |R(
ω
+ 2)| = a
α
.
The proof follows from transfinite induction on
α.
The following theorem is an example of showing that all mathematics takes
place in the class WF.
Theorem 3.4.10.
(1)
Every group is isomorphic to a group in
WF
.
(2) Every topological space is homeomorphic to a topological space in WF.
Proof: A group is an ordered pair (G,
× ) where × : G × G → G. Theorem
3.4.6 therefore implies that
(3.65)
If (
G
, × ) is any group, let α = |
G
| and let ƒ be a 1–1 mapping from α onto G.
Define an operation
ξ
on α by η = ƒ
–1
(
ƒ
(
ξ
)
×
ƒ
(
η)). Then (α
,
) is a group

94
Chapter 3
isomorphic to (
G
, × ). The same idea can be used to prove (b). We leave the proof
of (b) to the reader.
Generalizing the notion of well-orderings, we have the following: A relation
H is well-founded on a set A if and only if
(3.66)
The element y in Eq. (3.66) is called H -minimal in X. Thus, a relation H is
well-founded on A if and only if every nonempty subset of A has an H-minimal
element.
Theorem 3.4.11. If A
∈ WF, ∈ is well-founded on A.
Proof: Let X be a nonempty subset of A. Let
α = min{rank(y) : Y ∈ X }, and
pick a y
∈ X with rank(
y
) = α. Then y is ∈
-minimal in X by Theorem 3.4.3(a).
Theorem 3.4.12. If A is transitive and
∈ is well-founded on A, then A ∈ WF.
Proof: It is sufficient to show A
⊂ WF, because if A ⊂ WF, let α =
∪
{rank( y) + 1 : y ∈ x }; then x ∈ R (α), so x ∈ R(α + 1) ⊂ WF. If A ⊄ WF
,
let X = A
\
WF ≠ φ and let y be the ∈
-minimal in
X
. If z ∈ y, then z ∉ X
, but
z
∈
A
since A is transitive; so z ∈ WF . Thus, y ⊂ WF
, so
y
∈
WF
. This contradicts the
definition that y
∈ A\ WF
.
Let A be a set. By recursion on n, we define
(1)
∪
0
A = A.
(2)
∪
n
+ 1
A= ∪
(
∪
n
A
).
(3)
tr cl(
A) = ∪
{
∪
n
A :
n
∈ ω
}.
Here tr cl is the “transitive closure,” which is the least transitive set containing A
as a subset.
Theorem 3.4.13.
(a) A
⊂ tr cl
(
A
).
(b) tr cl(A
)
is transitive.
(c) If A ⊂ T and T is transitive, then tr cl(A) ⊂ T.
(d) If A is transitive, then tr cl(
A
) = A.
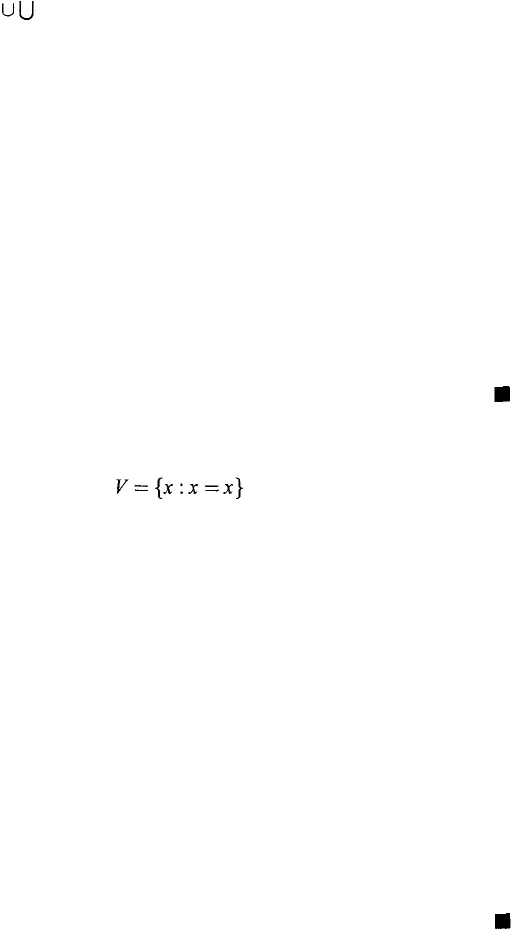
Axiomatic Set Theory
95
(e)
If x ∈ A, then tr cl(x
)
⊂
tr cl
(
A
).
(f)
tr cl(A) = A
{tr cl(
x
) :
x
∈
A
}.
The proof is straightforward from the definition of transitive closure.
Theorem 3.4.14. For any set A the following are equivalent:
(a)
A
∈
WF
.
(b)
tr cl(
A
)
∈
WF
.
(c)
∈ is well-founded on tr cl(A
).
Proof: (a) → (b). If A ∈ WF, then by induction on n, ∪
n
A ∈ WF since WF
is closed under the union operation (Theorem 3.4.6). Thus, each
∪
n
A
⊂
WF
, so
tr cl(A) ⊂ WF, so tr cl(A
)
∈
WF
.
The proof of (b)
→
(c) is Theorem 3.4.11.
(c) → (a). By (c) and Theorem 3.4.12, tr cl(A) ∈ WF, so A ⊂ tr cl(A
)
⊂
WF
,
so
A
∈
WF
.
Let V be the class defined by
(3.67)
In other words, V is the class of all sets. If we are convinced by the previous
theorems that all mathematics takes place in WF, it is reasonable to adopt as an
axiom the statement that V = WF. This does not mean that the two classes V and
WF
are really identical, but only that we restrict our domain of discourse to be just
WF
. In the following, we discuss some of the consequences of adding the axiom
V = WF to the axiom system of ZFC axioms except Regularity.
Theorem 3.4.15. The following are equivalent:
(a)
The axiom of regularity.
(b) ∀
A
(
∈ is well-founded on A).
(c) V = WF.
Proof: (a)
↔ (b) is immediate from the definition of well-founded relations.
For (b)
→
(c), (b) implies that for any
A
,
∈
is well-founded on tr cl(
A
), so
A
∈
WF
.
For (c)
→
(b), apply Theorem 3.4.11.
Unlike the other axioms of
ZFC, Regularity has no application in ordinary
mathematics, since accepting it is equivalent to restricting our attention to WF,
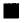
96
Chapter 3
where all mathematics takes place. In Chapters 5 and Chapter 9, we will see how
the Axiom of Regularity can be used to study level structures of general systems.
Since Regularity is equivalent to V = WF =
∪{R
(
α
) :
α ∈
ON
}, it gives us a
picture of all sets being created by an iterative process, starting from nothing.
Theorem 3.4.16. A is an ordinal if and only if A is transitive and totally ordered
by
∈
.
Proof: To see that ∈ well-orders A, let X be any nonempty subset of A. Then
Regularity implies there exists an
∈-minimal element in X.
3.5. References for Further Study
There are many good books in the area of axiomatic set theory, such as (Drake,
1974; Engelking, 1975; Fraenkel et al., 1973; Jech, 1978; Kleene, 1952; Kreisel and
Krivine, 1967; Kunen, 1980; Kuratowski and Mostowski, 1976; Kurepa, 1936c;
Martin and Solovay, 1970; Quigley, 1970; Rudin, 1977; Shoenfield, 1975; Suslin,
1920).
CHAPTER 4
97
Centralizability and Tests of
Applications
The concept of centralized systems is written in the language of set theory in
order to take advantage of the rigorous mathematical reasoning. The concept of
centralizable systems is introduced. Applications of the concept in sociology,
concerning the existence of factions in human society, public issues of contention,
and importance level of problems versus media, are listed. Two real-life examples
are given to illustrate the results obtained in this chapter. At the end some open
questions are posed.
4.1. Introduction
Hall and Fagen (1956) introduced the concept of centralized systems, where a
centralized system is a system in which one object or a subsystem plays a dominant
role in the system operation. The leading part can be thought of as the center of
the system, since a small change in it would affect the entire system, causing
considerable changes. Lin (1988a) applied the concept of centralized systems
to the study of some phenomena in sociology. Several interesting results were
obtained, including the argument on why there must be a few people in each
community who dominate others. In this chapter we look at the overall study of
the concept of centralized systems, related concepts, and some applications.
n = n(
r
), a function of
r
, called the length of the relation r, such that r ⊆ M
n
,
In the rest of this section, all necessary concepts of systems theory and termi-
nology of set theory will be listed in order for the reader to follow the discussions.
A system is an ordered pair of sets, S = (M,R), such that M is the set of all
objects of S, and R is a set of some relations defined on M. The sets M and R
are called the object set and the relation set of S, respectively. Here, let r
∈ R
be a relation of S. Then r is defined as follows: There exists an ordinal number

98
Chapter 4
where
is the Cartesian product of n copies of M.
A system S = (
M,R
) is trivial (resp., discrete) if M = R = Ø (resp., M ≠ Ø
and either R = Ø or R = {Ø
}).
G
iven two systems S
i
= (
M
i
,R
i
), i = 1,2,S
1
is
a partial system of S
2
if either (1) M
1
= M
2
and R
1
⊆ R
2
or (2) M
1
⊆
M
2
and
≠
there exists a subset R' ⊆ R
2
such that R
1
= R'
⏐
M
1
≡ {ƒ : ƒ is a relation on M
1
and there exists g ∈ R' such that ƒ is the restriction of g on M
1
}. In symbols,
R'
⏐M
1
= {ƒ : g ∈ R'(ƒ = g⏐M
1
}, where
. The system S
1
is a
subsystem of S
2
if M
1
⊆ M
2
and for each relation
r
1
∈R
1
there exists a relation
r
2
∈
R
2
such that
r
1
⊆
r
2
⏐
M
1
.
A system S = (M,R
)
h
as n levels, where n is a fixed whole number, if (1)
each object S
1
= (M
1
,R
1
) in M is a system, called the first-level object system;
(2) if is an (n – 1)th-level object system, then each object
is a system, called the n
th-level object system of
S
.
Let
S
i
= (
M
i
,R
i
), i = 1,2, be two systems and h : M
1
→
M
2
a mapping. By
transfinite induction, two classes
, i =
1, 2, and a class mapping
can be defined with the properties
and for each x =
where Ord is the class of all ordinals. For each relation
is a relation on M
2
with length n(
r
). Without confusion, h will be used to indicate
the class mapping and h is a mapping from the system S
1
into the system
S
2
,
denoted by h : S
1
→ S
2
. When h : M
1
→ M
2
is surjective, injective, or bijective,
the mapping h : S
1
→
S
2
is also surjective, injective, or bijective, respectively.
The systems S
i
are similar if there exists a bijection h : S
1
→ S
2
such that
The mapping
h
is called a similarity mapping from
S
1
onto
S
2
. Evidently, if h is a similarity mapping from S
1
onto S
2
, the inverse
h
–1
is a similarity mapping from
S
2
onto S
1
. A mapping h : S
1
→
S
2
is termed a
homomorphism from
S
1
into S
2
, if h (R
1
) ⊆ R
2
.
Note that a theorem followed by (ZFC) means that the theorem is true only
under the assumption that the ZFC axioms are true, where ZFC stands for the
Zermelo–Fränkel system with the axiom of choice. For set X,
⏐X⏐ denotes the
Centralizability and Tests of Applications
99
cardinality of X. A cardinal number α = ℵ
λ
is called regular if for any sequence of
ordinal numbers {α
β
<
ℵ
λ
: β < λ
} , the limit of the sequence is less than
ℵ
λ
. For
details and other terminology of set theory, see (Kuratowski and Mostowski, 1976).
4.2. Centralized Systems and Centralizability
To use the mathematical reasoning to study centralized systems, Lin
(submitted) redefined the concept in the language of set theory as follows.
Definition 4.2.1.
A system
S
= (
M,R
) is called a centralized system if each object
in S is a system and there exists a nontrivial system C = (M
C
,R
C
) such that for
any distinct elements x and y
∈ M , say x = (M
x
,R
x
) and y = (M
y
,R
y
), then
M
C
= M
x
∩
M
y
and
the system C is called a center of S.
Theorem 4.2.1 [ZFC (Lin and Ma, 1993)]. Let
κ be an arbitrary infinite car-
dinality and
θ > κ a regular cardinality such that for any ordinal number
Assume that S = (
M,R
) is a system sat-
isfying
⏐
M
⏐ ≥ θ and each object m ∈ M is a system with m = (
M
m
,R
m
) and
⏐M
m
⏐ < κ
.
If there exists an object contained in at least
θ
objects in M, there then
exists a partial system S' =
(
M',R'
) of S such that S' forms a centralized system
and
⏐
M'
⏐ ≥ θ
.
This result is a restatement of the well-known
∆
-lemma in axiomatic set theory
(Kunen, 1980). The following question, posed by Dr. Robert Beaudoin, is still
open.
Question 4.2.1. A system S = (
M,R
) is strongly centralized if each object in S is
a system and there is a nondiscrete system C =
(
M
C
, R
C
) such that for any distinct
elements x and y
∈ M, say x = (M
x
,R
x
) and y = and
Give conditions under which a given system has a partial
system which is strongly centralized.
A system S
0
is n
-level homomorphic to a system
A
, where n is a fixed natural
number, if there exists a mapping h
S
:
S
0
0
→ A
, called an n
-level homomorphism,
satisfying the following:
(1) The systems
S
0
and A have no nonsystem kth-level objects, for each k < n.
(2)
For each object S
1
in
S
0
, there exists a homomorphism h
S
1
from the object
system
S
1
into the object system h
S
0
(
S
1
).
(3)
For each i < n and each ith-level object S
i
of S
0
, there exist level object
systems S
k
, for k = 0, 1, ... , i – 1, and homomorphisms h
S
, k = 1, 2, ... , i,
k
such that
S
k
is an object of the object system S
k –1
and h
S
k
is a
homomorphism from
S
k
into h
S
k–1
(
S
k
)
, for k = 1, 2, ... , i.
