Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.


80
Chapter 3
A partial order is a pair (P, ≤) such that P ≠ Ø and ≤ is a relation on P which
is transitive and reflexive (
∀
ρ ∈ P (ρ ≤ ρ)) . p ≤ q is read “
p
extends
q.
” Elements
of p are called conditions. A partial order (P,
≤) is a partial order in the strict
sense, if it, in addition, satisfies
(3.33)
We often abuse notation by referring to “the partial order P” or “the partial order
≤” if ≤ or P is clear from context.
If (
P,
≤
) is a partial order, p and q ∈ P are compatible if
(3.34)
They are compatible, denoted by p
⊥
q if ¬∃r ∈ P
(
r ≤ p
∧
r ≤ q
). An antichain in
P is a subset A ⊂ P such that ∀p, q ∈ A (p ≠ q → p ⊥ q
). A partial order (
P, ≤) has
the countable chain condition (ccc) if every antichain in P is countable.
A subset G
⊂ P is called a filter in P if
Axiom 3.3.1 [Martin’s Axiom].
MA(
κ
) is the statement: Whenever (
P,
≤
) is a
nonempty ccc partial order and is a family of at most
κ
many coinitial subsets of
P,
then there is a filter
G
in
P
such that
MA is the statement
Example 3.3.1. Let P be the set of all finite partial functions from
ω to 2; i.e.
(3.35)
Define p ≤ q by q ⊂ p; i.e., the function p extends the function q. Now p and q
are compatible if and only if they have the same values on the set
D
(
p
)
∩
D
(
q
), in
which case
p
∪
q
is a common extension of both
p
and
q.
The partial order (
P,
≤
) has ccc. In fact, let D ⊂ P be an antichain in P then
⏐
D
⏐ ≤ ⏐
P
⏐
=
ω. If G is a filter in P, the elements of G are pairwise compatible.
Hence, if we let ƒ = ƒ
G
= G then ƒ
G
is a function with D(ƒ
G
) ⊂ ω In this
example, we are more interested in ƒ than G. If p
∈ P, we think of p as a finite
approximation to ƒ, and we say intuitively that p forces “p
⊂ ƒ” in the sense that
if p
∈ G, then p ⊂ ƒ
G
. So p says what f is restricted to D
(
p
). If q ≤ p, then q says
more about ƒ than p does.
D
(ƒ
G
) could be a very small subset of
ω;
for example, Ø is a filter and
Ø = Ø
the empty function. However, by requiring that G intersect many coinitial sets,
we can make ƒ
G
representative of typical functions. For example, let
(3.36)

Axiomatic Set Theory
81
for each n ∈ ω. Since each p ∈ P can be extended to a condition with n in its
domain,
D
n
is coinitial in
P.
If
∀
n
∈ ω
(
G
∩
D
n
≠ Ø), then ƒ
G
has a domain equal to
ω. Let E =
{
p ∈ P : ∃n ∈ D
(
p
)(
p
(
n
) = 1)}. E is coinitial in P; and if G
∩
E ≠ Ø,
then ƒ
G
takes the value 1 somewhere.
Let h : ω → 2 be a fixed mapping. Define
(3.37)
Then
E
h
is coinitial in P; and if G
∩
E
h
≠ Ø, then ƒ
G
≠ h. Let
={
D
n
: n ∈
ω
}
∪
{
E
h
: h ∈
ω
2
}; then
⏐
⏐
= 2
ω
. If G is a filter in P and G
∩
D ≠ Ø
∀
D
∈
,
then ƒ
G
is a function from ω to 2, which is impossible.
This fact shows the next result.
Theorem 3.3.5. MA(2
ω
) is false.
Theorem 3.3.6.
(a) If
κ < κ', then MA(
κ
') → MA(
κ
).
(b)
MA(
ω) is true.
Proof: (a) is clear. For (b), let = {
D
n
: n ∈ ω} and define, by induction
on n, P
n
∈ P so that P
0
is an arbitrary element of P (since P ≠ Ø) and P
n +1
is
any extension of P
n
such that P
n +1
∈ D
n
. This is possible since D
n
is dense.
So P
0
≥ P
1
≥ P
2
≥
…
. Let G be the filter generated by {
P
n
: n ∈ ω}; i.e.,
G = {q
∈ P : ∃
n
(
q ≥ P
n
)}. Then G is a filter in P and G
∪
D
n
≠ Ø for each
n
∈ ω
.
Theorem 3.3.6(b) implies that MA follows from CH, because we can view MA
as saying that all infinite cardinals < 2
ω
have properties similar to ω.
Since the proof of Theorem 3.3.6(b) did not need the fact that P was ccc, we
might attempt to strengthen MA(
k
) by dropping this requirement, but for k > ω
this strengthening becomes inconsistent by the next example.
Example 3.3.2. Let
(3.38)
If G is a filter in P, then, as in Example 3.3.1,
G
is a function with
D
( G ) ⊂ ω
and R
(
∪
G
) ⊂ ω
1
. If α < ω
1
, let
(3.39)
Then D
α
is coinitial in P. We claim that no filter G in P could intersect each D
α
,
α < ω
1
, since that would mean that R
(
G) = ω
1
, contradiction. Of course, P
here is not ccc since the conditions {(0,
α
) :
α ∈ ω
1
} are pairwise incompatible.

82
Chapter 3
We now proceed to show how MA is applied to answer Questions 3.3.1 and
3.3.2.
Theorem 3.3.7. Assume MA(
k). Let
where and as-
sume that for all
and all finite Then there is d
⊂ ω
such that
Proof: Define a partial order P
by
(3.40)
where (
s
1
,F
1
) ≤ (
s,F
)
if and only if
(3.41)
Then the partial order
has the ccc. In fact, for (s
1
,
F
1
) and (s
2
,
F
2
)
∈
P
,
they are compatible if and only if
(3.42)
Suppose that
were pairwise incompatible. By Eq. (3.42),
the sets s
would all be distinct, which is impossible.
For each x
∈
, define
(3.43)
Then D
x
is coinitial in P
. In fact, for each
For any
(3.44)
E
n,y
is coinitial in P
, since for each
If we pick
with m > n, then
F
) is an extension of (
s, F
) in
E
n,y
.
By MA(
k ), there is a filter G in P
intersecting all sets in
(3.45)
Let
Then
In fact,
If
then (
s', F'
) and (
s, F
) are compatible. Eq. (3.42) implies that
(3.46)
This implies that
If
is infinite.
Question 3.3.2 now can be answered by the following corollary.

Axiomatic Set Theory
83
Corollary 3.3.1.
Let
⊂ P(ω) be an almost disjoint family of power κ, where
Assume MA(
κ). Then is not maximal.
Proof: Let
Then since is almost disjoint it follows that
ω for all finite F ⊂ Thus, Theorem 3.3.7 implies that there is an infinite
almost disjoint from each member of
Theorem 3.3.8. Let
⊂ P(ω) be an almost disjoint family of size κ, where ω ≤
κ
< 2
ω
. Let
⊂
If
MA(
κ
),
then there is a d
⊂ ω
such that
and
Proof: Apply Theorem 3.3.7 with
Corollary 3.3.2. MA(
κ
)
→
2
κ
= 2
ω
.
Proof:
Fix any almost disjoint family of size
κ
( exists by Theorem 3.3.3).
Define
Theorem 3.3.8 says
that
Φ is onto, so
Corollary 3.3.3. Iƒ MA, then 2
ω
is regular.
Proof: If κ < 2
ω
, then 2
κ
= 2
ω
, so by König’s theorem, cf(2
ω
) > κ.
Corollary 3.3.4. MA( )
κ
is equivalent to MA(
κ
) restricted to partial orders of
cardinality
κ.
Proof: Assume the restricted form of MA(
κ
), and let (
Q,
be a ccc partial
order of arbitrary cardinality, and
a family of at most κ many coinitial subsets of
Q. We shall find a filter H in Q intersecting each
by applying the restricted
form of MA(
κ
) to a suitable suborder P
⊂
Q
with
We first show that we can find P ⊂ Q such that
(1)
(2) DP is coinitial in P for each
(3)
If
p, q
∈ P, p and q are compatible in P if and only if they are compatible
in Q.
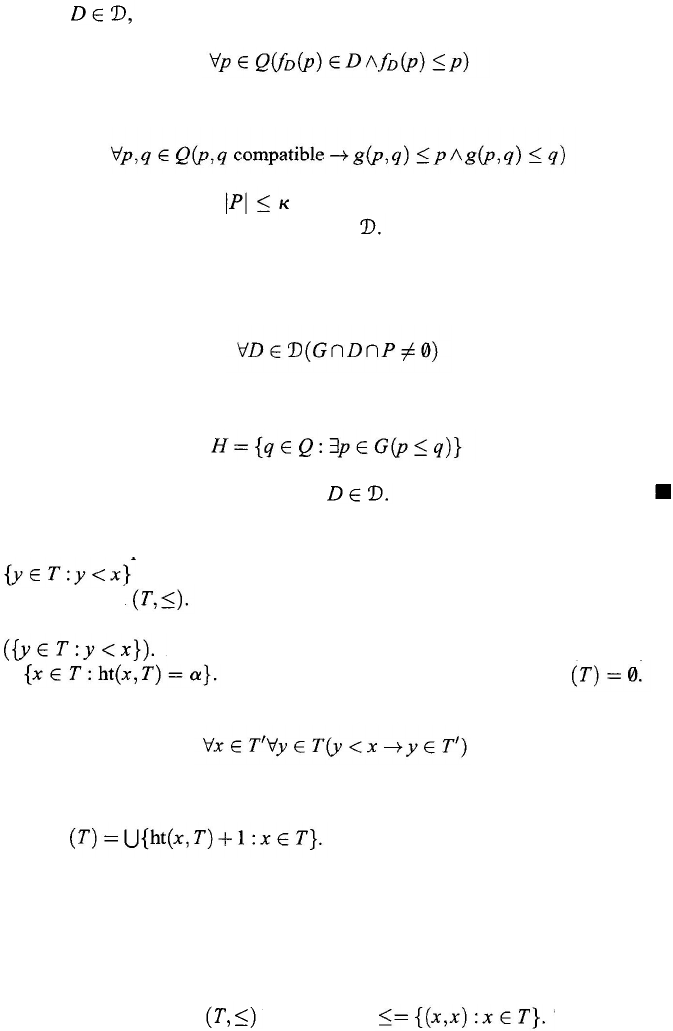
84
Chapter 3
For
let f
D
: Q → Q be such that
(3.47)
and let g : Q × Q → Q be such that
(3.48)
Let P ⊂ Q be such that
and P is closed under g and each f
D
; i.e.,
g (P
× P) ⊂ P and f
D
(P) ⊂ P, for all D ∈ P satisfies (3) by closure under g
and (2) by closure under f
D
.
Statement (3) implies that P has the ccc, so by applying the restricted MA(k)
to P, let G be a filter in P such that
(3.49)
If H is the filter in Q generated by G, i.e.,
(3.50)
then H is a filter in Q intersecting each
A tree is a partial order in the strict sense (T,
≤ ) such that, for each x ∈ T,
is well-ordered by
≤. As usual, we abuse notation and refer to T
when we mean
Let T be a tree. If x
∈ T, the height of x in T, denoted by ht(x, T ), is type
For each ordinal
α, the αth level of T, denoted by Lev
α
(
T ),
is
Then ht(
T
) is the least α such that Lev
α
A
subtree of T is a subset T
'
⊂ T with the induced order such that
(3.51)
Proposition 3.3.1.
(a) ht
(b) If T
' is a subtree of T, then for each x
∈ T
', ht(
x, T
) = ht(x, T' ).
The proof is immediate from the definitions involved.
Example 3.3.3.
(a) Let a partial order
be defined by
Then
ht(
x, T
) = 0 for all x ∈ T and ht(
T
) = 1.
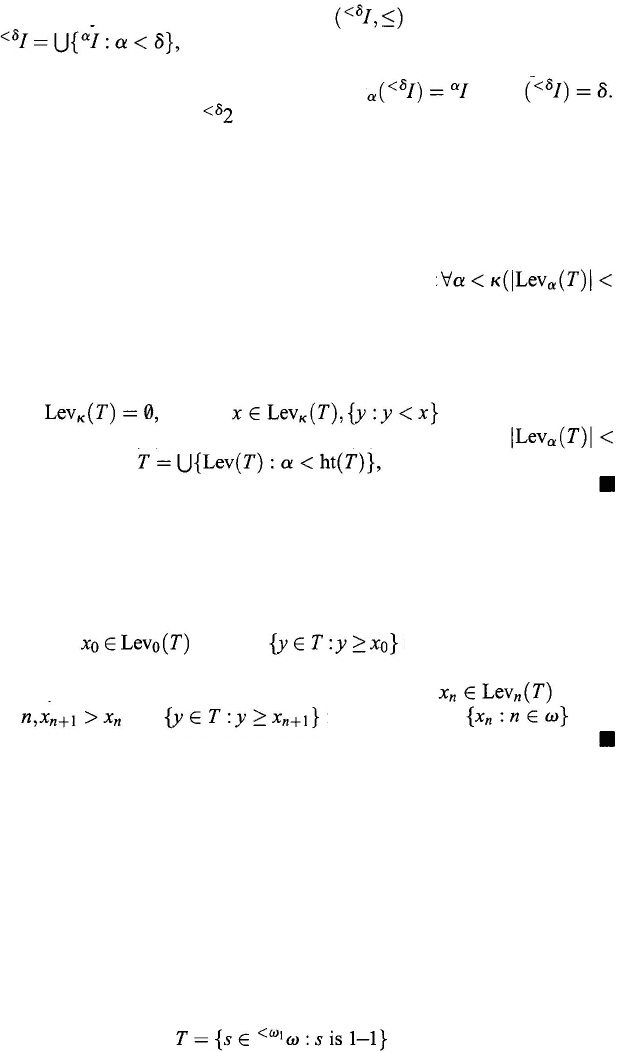
Axiomatic Set Theory
85
(b) Let I be any set and δ an ordinal. A tree
is defined as follows:
and s ≤ t if and only if s ⊂ t. This tree is called the
complete I-ary tree of height
δ. We think of elements of
α
I as sequences of
elements of I of length
α. If α < δ, then Lev
and ht
When I = 2, we refer to
as the complete binary tree of height
δ.
For any infinite cardinal κ, a κ-Suslin tree is a tree T such that ⎟T ⎟ = κ and
every chain and every antichain of T have cardinality <
κ. Suslin trees were
introduced by Kurepa (1936c). We first continue with a general discussion of
κ-Suslin trees and related concepts. We confine our attention to the case when κ
is regular. When
κ
is singular,
κ
-Suslin trees exist but are of little interest.
For any regular
κ,
a
κ
-tree is a tree
T
of height
κ
such that
κ).
Theorem 3.3.9. For any regular
κ, every κ-Suslin tree is a κ
-tree.
Proof: since if would be a chain of
cardinality
κ. Thus, ht(T ) ≤
κ.
Since each Lev
α
( T) is an antichain,
κ. Since ⎟T⎟ = κ and
regularity of
κ implies that
ht(T ) =
κ.
Theorem 3.3.10 [König’s Theorem]. If T is an ω-tree, then T has an infinite
chain.
Proof:
Pick
such that
is infinite. This is possible
since Lev
0
(
T) is finite, T is infinite, and every element of T is
≥ some element of
Lev
0
(T
). By a similar argument, we may inductively pick
so that
for each
and
is infinite. Then
is an
infinite chain in T.
For any regular
κ, a κ-Aronszajn tree is a κ-tree such that every chain in T is
of cardinality <
κ. Thus, each κ-Suslin tree is a κ-Aronszajn tree, but Theorem
3.3.10 says that there are no
ω-Aronszajn trees. At ω
1
the situation is different.
The existence of an
ω -Suslin tree is independent of ZFC, but there is always an
1
ω
1
-Aronszajn tree.
Theorem 3.3.11. There is an ω
1
-Aronszajn tree.
Proof: Let
(3.52)

86
Chaper 3
Thus,
T
is a subtree of
The ht(T
) =
ω
1
,
since for every
α
<
ω
1
,
there is a 1–1
function from
α
into
ω.
If
C
were an uncountable chain in
T,
then
C
would be a
1–1 function from ω
1
into ω; thus, every chain in T is countable. Unfortunately, T
is not Aronszajn since
T
is not an
ω
1
-tree; Lev
α
(
T
) is uncountable for
However, we can define a subtree of T which is Aronszajn.
If s, t
∈
α
ω,
define
s
~ t if and only if the set
is finite.
We will find s
α
for each α < ω
1
such that
Assuming such s
α
may be found, let
(3.53)
By (ii), T* is a subtree of T. By (i), each s
α
∈
T*
so Lev
α
for each α < ω
1
.
Unlike T, T* is an
ω
l
-tree since
is countable. Thus, T* is an
ω
1
-Aronszajn tree.
We now see how to construct the sequence {s
α
} by induction. Given s
α
, take
any
and let it is here (iii) is used. Now suppose
that we have s
α
for α < γ , where γ is a limit ordinal. Fix so that
and and inductively define
so that and Let
Then
and
t
is 1—1; if we set
then (i) would hold for
and
Then
so
(iii) holds as well.
A well-pruned
κ-tree is a κ-tree T such that
and
(3.54)
Theorem 3.3.12. If κ is regular and T is a κ-tree, then T has a well-pruned
κ
-subtree.
Proof:
Let T
1
be the set of x ∈ T such that
(3.55)
Then T
1
is clearly a subtree of
T.
To verify Eq. (3.54) for
T
1
, let us fix
x
∈
T
1
and
α
such that ht(
x, T
) < α < κ. Let
By definition of
T
1
and the fact that each
has cardinality

Axiomatic Set Theory
87
κ, and each element of this set is above some element of Y. Since ⏐Y⏐ < κ, there
is y
∈ Y such that and this y is in T ¹ . A similar argument
shows that
Now for every
is a well-pruned subtree of T.
Theorem 3.3.13.
If κ is regular, T is a well-pruned κ-Aronszajn tree, and x ∈ T,
then
(3.56)
Proof:
For n = 2, this follows from the fact that {y : y > x} meets all levels
above x and cannot form a chain. For n > 2, we proceed by induction. If the
theorem holds for n, fix
α > ht(
x,
T
)
and distinct y
1
,
y
2
, . . . ,
y
n
∈
Lev
α
(T) with
each
y
i
> x. Now let β > α be such that there are distinct z
n
,
z
n +1
∈
Lev
β
(
T ) with
z
n
,
z
n+1
>y
n
. For
i
<
n,
there are
z
i
∈
Lev
β
(
T
) with
z
i
>
y
i
. Then {
z
1
,
z
2
, . . . ,
z
n +1
}
establishes the theorem for n+1.
A topological space (Engelking, 1975) is a pair (
X
,T) consisting of a set X
and a family T of subsets of X satisfying the following conditions:
(i) ø
∈ T and X ∈ T.
(ii) If U
∈ T and V ∈ T , then U ∩ V ∈ T.
(iii)
If
⊂ T, then
∪
∈ T.
The set X is called a space, the elements of X are called points of the space,
and the subsets of X belonging to T are called open in the space. The family T is
also called a topology on
X.
Let (
X
,
≤
) be a total ordering. The order topology T, or the topology induced
by the ordering
≤
, on the set X is the topology generated by the following sets,
called intervals: For
a
, b ∈ X satisfying a < b, let
(3.57)
(3.58)
and
(3.59)
That is, each element in T is either a union on a finite intersection of some sets of
the forms in (3.57)–(3.59).

88
Chapter 3
A topological space has ccc, if each collection of pairwise disjoint open sets of
the space is countable; it is separable if it has a countable subset A such that each
nonempty open set intersects A.
A Suslin line is a total ordering (X,
≤) such that in the order topology X is ccc
but not separable. Suslin’s hypothesis (SH) states that “there are no Suslin lines.”
SH arose in an attempt to characterize the order type of the real numbers (R, <).
It was well known that any total ordering (X,
≤
) satisfying
(a) X has no first and no last elements,
(b)
X is continuous, and
(c) X is separable in the order topology
is isomorphic to (R, <) (see Theorems 3.4.5 and 3.4.7). Suslin (1920) asked
whether (c) may be replaced by
(c') X is ccc in the order topology.
Clearly, under SH, (c) and (c’) are equivalent, and one can show that if there is a
Suslin line, then there is one satisfying (a) and (b). Thus, SH is equivalent to the
statement that (a), (b), and (c’) characterize the ordering (R, <).
Theorem 3.3.14.
There is an
ω
1
-Suslin tree if and only if there is a Suslin line.
Proof: First, let T be an
ω
1
-Suslin tree. By Theorem 3.3.12, we can assume
that T is well-pruned. Let
L = {C
⊂ T : C is a maximal chain in T }
(3.60)
If C
∈ L, there is an ordinal h(
C
) such that C contains exactly one element from
Lev
α
(
T ) for α < h
(
C
) and no elements from Lev
α
(T ) for
α ≥ h
(
C). Since T is
Aronszajn, h(C) <
ω
1
. Since T is well-pruned, a maximal chain cannot have a
largest element, so each h(C) is a limit ordinal. For
α < h(
C
), let C
(
α) be the
element of C on level
α.
We order L as follows: Fix an arbitrary total order < of T. If C, D
∈ L, C ≠ D,
let d
(
C,D ) be the least α such that C (α) ≠ D(α). Observe that d (
C,D
) <
min{h
(
C), h
(
D
)}. Let C D if and only if C(d(C,D )) < D (d(
C,D
)). We have
thus defined an order on L. It is easily verified that it is indeed a total order of L.
We now show that (
L,
) is a Suslin line.
First, we show that L has the ccc. Suppose that is a family
of disjoint nonempty open intervals. Pick
and
α
ξ
so that
(3.61)
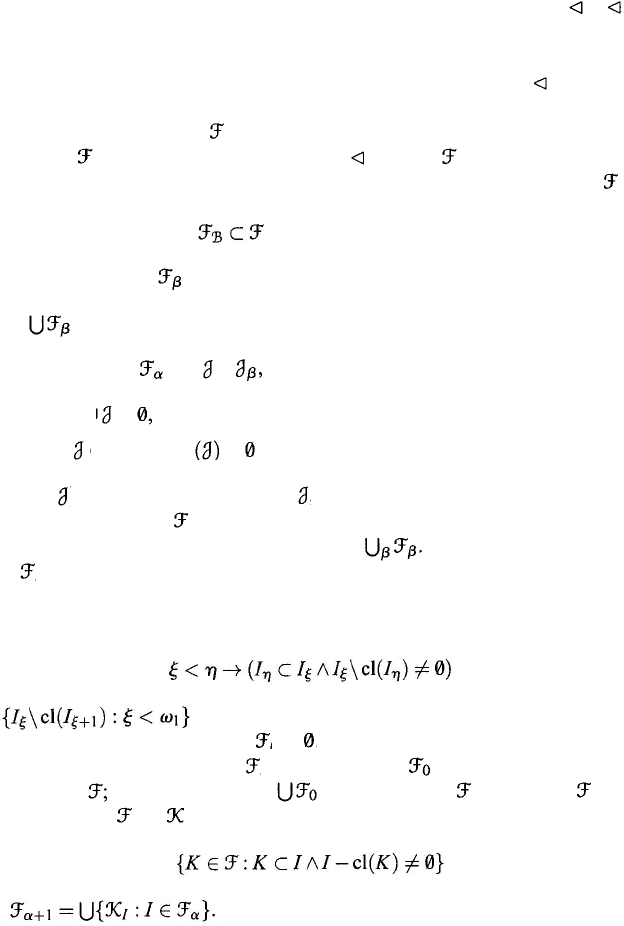
Axiomatic Set Theory 89
then {
E
ξ
(α
ξ
) : ξ < ω
1
} forms an antichain in T, contradicting that T is a Suslin
tree.
To show that L is not separable, it is sufficient to see that for each δ < ω
1
,
{C : h
(
C) < δ} is not dense in L. Fix x ∈ Lev
s
(T ). By Theorem 3.3.13, there
exists an
α
>
δ
with three distinct elements,
y, z, w
∈
Lev
α
( T) above x. Let D, E, F
be elements of L containing y, z, w, respectively. Say they are ordered D
E
F
then (D, F) is a nonempty interval, but since
x
∈
D
∩
F, (
D, F
)
contains no C
∈ L
with h
(
C
) < δ.
On the other hand, suppose that we are given a Suslin line ( L, ). We may
assume that L is densely ordered by putting gaps in the set and no nonempty open
subset of L is separable. Let
be the set of all nonempty open intervals of
L
; thus,
elements of are of the form (a, b), where a b. Then is partially ordered by
reverse inclusion: I
≤ J if and only if I ⊃ J. We will define a subset T ⊂ so
that
≤ is a Suslin tree ordering on T.
To find
T,
we first find
for each β < ω1 so that for each β,
(1) the elements of are pairwise disjoint,
(2) is a dense subset in L, and
(3) if
α < β, I ∈
and
∈ then either
(a)
I
∪
=or
(b)
⊂
I
and
I
\cl
≠
where cl( ) stands for the closure of , which is the smallest subset Y whose
complement belongs to
.
Assuming that this can be done, we let T = By (1)–(3), T is a tree and
each
β = Lev
β
(T ). If A ⊂ T is an antichain, then the elements of A are pairwise
disjoint, so |A|
≤ ω. T can have no uncountable chains, since if {
I
ξ
: ξ < ω
1
}
were such a chain, with
ξ < η → I
ξ
≤ I
η
, then by (3)(b)
(3.62)
so
would contradict the ccc of L. Finally, |T| = ω1 , since
(2) implies in particular that each
β ≠ . Thus, T is a Suslin tree.
We now construct the sets
β by induction. is any maximal disjoint
subfamily of maximality implies is dense. Given
α
, we define
α+1 as
follows: For I
∈ , let I be a maximal disjoint subfamily of
(3.63)
Let
