Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.


Naive Set Theory
49
Proof: Let A, B, and C be the sets defined in the proof of Theorem 2.5.20.
Then by applying Theorem 2.5.10 to the ordered sums A + C and B + C we obtain
(2.95).
Theorem 2.5.22. Let α and β be ordinals. If α ≥ β, then there exists exactly one
ordinal
γ such that α = β + γ.
Proof: Let A = α, B be a segment of A of type β , and γ =
A
–
B.
Clearly,
α = β + γ. To prove the uniqueness of γ suppose that β + γ
1
= β + γ
2
. By (2.94)
this implies that
γ
1
≥ γ
2
and γ
2
≥ γ
1
. Thus, γ
1
= γ
2
by Theorem 2.5.8.
Theorem 2.5.23 [The First Monotonic Law for Multiplication].
(α < β)→(γα< γβ),
for
γ > 0
(2.96)
Proof: In fact,
γβ is the type of the Cartesian product B × C ordered lexico-
graphically, where B =
β and C = γ. Let A = α, and let A be a segment of B. The
Cartesian product A × C ordered lexicographically is a segment of B × C.
Theorem 2.5.24 [The Second Monotonic Law for Multiplication].
(α ≤ β) → (αγ ≤ βγ) (2.97)
Proof: Let A, B, and C be well-ordered sets of type
α, β, and γ
, respectively,
and we assume that A ⊂ B. Thus, C × A ⊂ C × B
, which proves Eq. (2.97).
It follows from the identity 1 ·
ω
= 2 ·
ω
that
≤
in Eq. (2.97) cannot be replaced
by < .
The operation of ordinal exponentiation is defined by transfinite induction as
follows:
(2.98)
(2.99)
(2.100)
where
λ is a limit ordinal. We say that γ
α
is the power of γ, γ is the base, and α
the exponent.
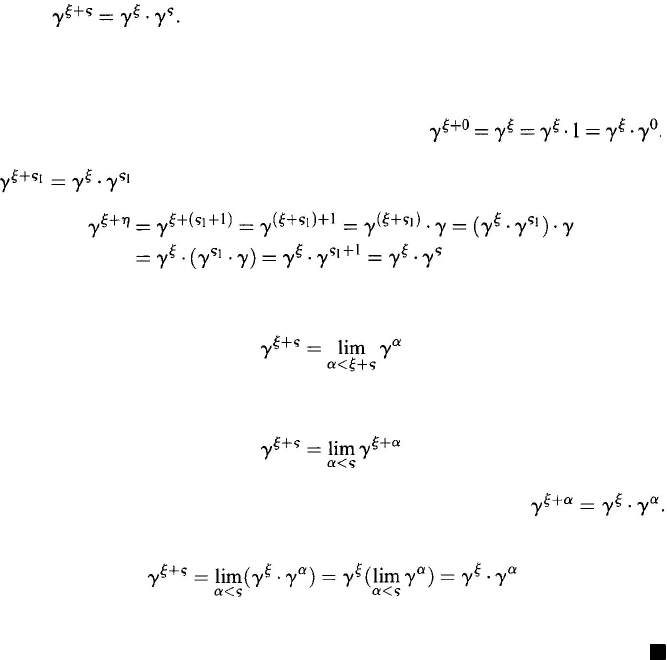
50
Chapter 2
(2.101)
(2.102)
Theorem 2.5.25. For any ordinals α, β , and γ with γ > 1,
α < β → γ
α
<γ
β
This follows from the definition.
Theorem 2.5.26. For any ordinals ξ, η , and γ , we have
γ
ξ+η
=γ
ξ
· γ
η
Proof: Given an ordinal ξ, let B denote the set of those ς ∈ W
(
η + 1) for
which
We shall show that if ς ≤ η, then
W
(ς) ⊂ B →ς∈B
(2.103)
In fact, the following three cases are possible: (i) ς = 0; (ii) ς is not a limit ordinal;
(iii)
ς
is a limit ordinal > 0. In case (i),
ς ∈
B
, because
In case (ii),
ς= ς
1
+1
where
ς
1
∈ W(ς);
thus, by assumption,
ς
1
∈
B.
Hence.
and therefore
which shows that ς ∈ B. Finally, in case (iii), ξ + ς is a limit ordinal; thus,
(2.104)
Because the sequence
γ
α
,α<ξ+ς,
is increasing when γ > 1,
(2.105)
Since for α < ς we have α ∈ W(ς ), it follows that α ∈ B; i.e.,
Thus,
which implies that ς ∈ B. Hence, implication (2.103) is proved. By induction it
follows that B = W
(
η
+ l
). Thus, η ∈ B. This proves Eq. (2.102).
Theorem 2.5.27. For any ordinals
ξ, η, and γ
,
(γ
ξ
)
η
=γ
ξη
(2.106)

Naive Set Theory
51
which shows that ς ∈ B. Finally, if ς is a limit ordinal > 0, then
we have
ς ∈ B. Hence Eq. (2.106) is proved.
Proof: This argument is analogous to that of the previous theorem. Let B
denote the set of those
ς ∈ W(
ς
that implication (2.103) holds. As before we consider cases (i)–(iii). In case (i),
ς ∈ B , because (γ
ξ
)
0
= 1 = γ
0
= γ
ξ
·0
. In case (ii) we have ς = ς
1
+ 1, where ς
1
satisfies the condition that (γ
ξ
)
ς
1
= γ
ξς
1
. This formula in turn implies
η + 1) for which (γ
ξ
) = γ
ξη
. It suffices to show
Theorem 2.5.28. For any given ordinal
γ > 1, every ordinal number α can be
uniquely represented in the form
where n is a natural number, and
η
i
and
β
i,
i = 1, 2, … , n, are ordinals such that
η
1
>
η
2
> … >
η
n
,
and
0
≤
β
i
< γ, for i = 1, 2 , … ,
n.
Proof: By transfinite induction it can be shown that for any ordinal α,
We now let ς be the smallest ordinal such that α < γ
ς
. If ς were a limit ordinal,
then
and γ
λ
≤ α for λ < ς
, which implies
γ
ς
≤ α.
This contradicts
the definition of ς. Thus, ς
=
η
1
+ 1, where
Notice that
there exists an ordinal pair (
β
1
, σ
1
)
∈
W
(γ
) ×
W(γ
η
1
) such that O
((
β
1
,
σ
1
)) = α, where
{
β
1
} × O (σ
1
). Therefore,
where
β
1
<
γ
and
σ
1
< γ
η
1
.
For the same reason, there exist ordinals η
2
< η
1
,
β
2
< γ,
and
σ
2
< γ
η
2
such that

52
Chapter 2
{
η
1
,
η
2
,...}
This procedure must stop within a finite steps because, otherwise,
would be a sequence of type *
ω
of ordinals numbers, and this contradicts Theorem
2.5.12. Therefore, there exists a natural number n such that
with the property that
Now we show the uniqueness of the expression. If
η
1
= ξ
1
, β
1
= θ
1
, and
where
n, and
j = 1,2,...,p. By the definition of η
1
and
ξ
1
, we must have
Repeating this procedure, we have n = p,
η
k
=
ξ
k
, and β
k
= θ
k
for k ≤ n.
Well-ordered sets owe their importance mainly to the fact that for each set there
exists a relation which well-orders the set. This theorem is also of the greatest
importance for the theory of cardinal numbers because it shows that all cardinal
numbers are comparable with each other.
Theorem 2.5.29 [Well-Ordering Theorem].
Every set can be well-ordered.
Proof:
Let f be a function defined on p(A) – where A is a nonempty set,
such that for each nonempty subset B
⊂ A, f (B) ∈ B. We can extend this function
to the whole power set p (A) by letting = p, where p is any fixed element
which does not belong to A.
Now let C denote the set of all relations R
⊂ A × A well-ordering their field.
Then there exists a set of all ordinals
β, where β = the order type of some R ∈ C.
Let
α be the smallest ordinal greater than every ordinal β in this set.
We now define a transfinite sequence of type
α by transfinite induction such
that
(2.107)
(2.108)
for each
If
for all
ξ < α we had then there would exist a transfinite sequence of type
α with distinct values belonging to A. This implies that there exists a relation on
A well-ordering a subset of A into type
α. But this contradicts the definition of α.
Therefore, there exists a smallest ordinal β such that ϕ
β
= p. This implies that
thus, A is the set of all terms of a transfinite sequence of type
β whose terms are all distinct. Consequently, there exists a relation well-ordering
A into type
β.

Naive Set Theory
53
Theorem 2.5.30.
If A and B are two arbitrary sets, precisely one of the following
holds:
i.e., any two cardinal numbers are comparable with each other.
The proof follows from the well-ordering theorem and Theorem 2.5.8.
By Theorem 2.5.30, every set of cardinal numbers can be ordered according
to the increasing magnitude of its elements. This ordered set will prove to be
actually well-ordered. For this and similar considerations concerning cardinal
numbers, it is practical to represent the cardinal numbers by means of ordinal
numbers. According to the well-ordering theorem, every cardinal number can be
represented by a well-ordered set; briefly, every cardinal number can be represented
by an ordinal number. The totality of ordinal numbers which represents the same
cardinal number
ℵ is designated the number class Q(
ℵ
)
, where Q (
ℵ
)
contains a
smallest ordinal, which is called the initial number of Q(
ℵ
) or the initial number
belonging to
ℵ.
Theorem 2.5.31. Every transfinite initial number is a limit number.
Proof: If some transfinite initial number were not a limit number, it would be
immediately preceded by an ordinal number
γ, and the initial number would be
γ + 1. But then γ and γ + 1 would have the same cardinal number; i.e., γ + 1
would not be the smallest ordinal number in its number class, contradiction.
Theorem 2.5.32. Every set of cardinal numbers, ordered according to increasing
magnitude, is well-ordered. There exists a cardinal number which is greater than
every cardinal number in the set.
Proof: For the first part of the assertion we have to show that every nonempty
subset of cardinal numbers contains a smallest cardinal number. This is, however,
clear if every cardinal number is represented by the initial number belonging to
it. Among these initial numbers then there is, as in every nonempty set of ordinal
numbers, a smallest one, and the corresponding cardinal number is the smallest
cardinal number in the set.
The second part of the assertion follows from Theorems 2.5.11 and 2.1.4.
If the family of all transfinite cardinal numbers is ordered according to increas-
ing magnitude, then we denote the smallest transfinite cardinal number by ℵ
0
, the
next by
ℵ
1
, etc. In general, every transfinite cardinal number receives as index
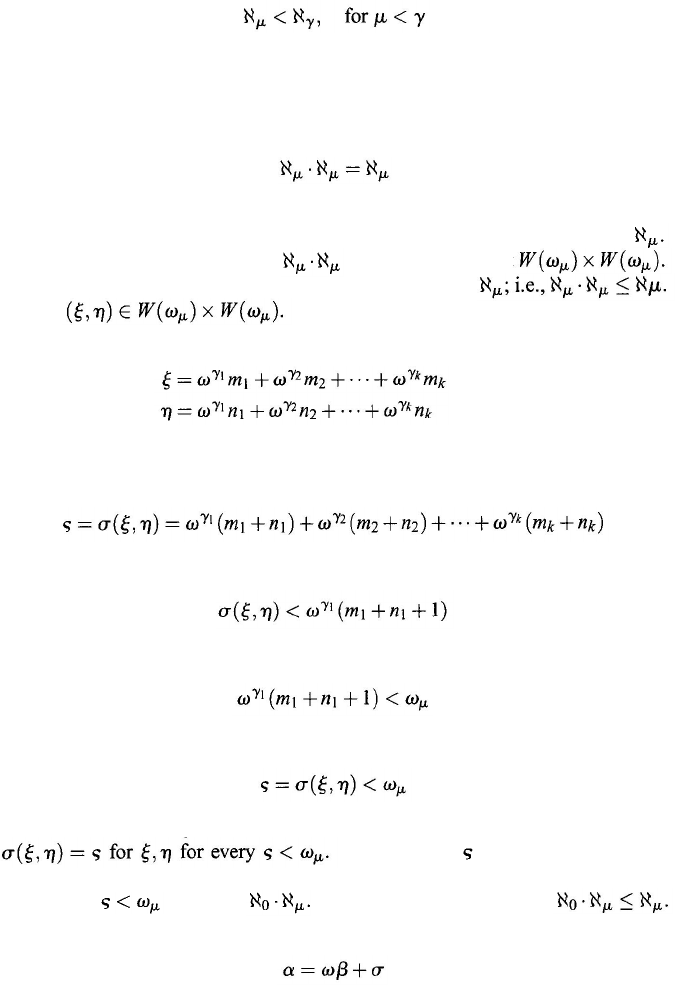
54
Chapter 2
the ordinal number of the set of transfinite cardinal numbers which precede the
cardinal number in question. Therefore,
(2.109)
The initial number which belongs to
ℵ
µ
is denoted by
ω
µ
. Then ω
0
is the smallest
transfinite limit number and is therefore the same as the
ω introduced before.
Theorem 2.5.33. For any ordinal µ > 0,
(2.110)
Proof:
The set W
(
ω
µ
) has order type ω
µ
and is therefore a set of power
Consequently, the cardinal number
is the power of the set
We now show that this set has at most the cardinal number
Let
Then by Theorem 2.5.28 and adding whatever
necessary terms with coefficient 0, we can represent ξ and η uniquely in the form
(2.111)
where γ
1
> γ
2
>
...
>
γ
k
and for all i ≤ k either m
i
> 0 or n
i
> 0. Define a
polynomial
Since only a finite number of nonzero terms appear, it follows that
and the proof of Theorem 2.5.28 implies that
Consequently,
We therefore certainly obtain all number pairs
ξ, η by solving the equation
But for every this equation has only
a finite number of solutions. Therefore, the cardinal number of the set of all solu-
tions for all is at most
We now need only show that
Theorem 2.5.28 implies that for any ordinal α,
(2.112)
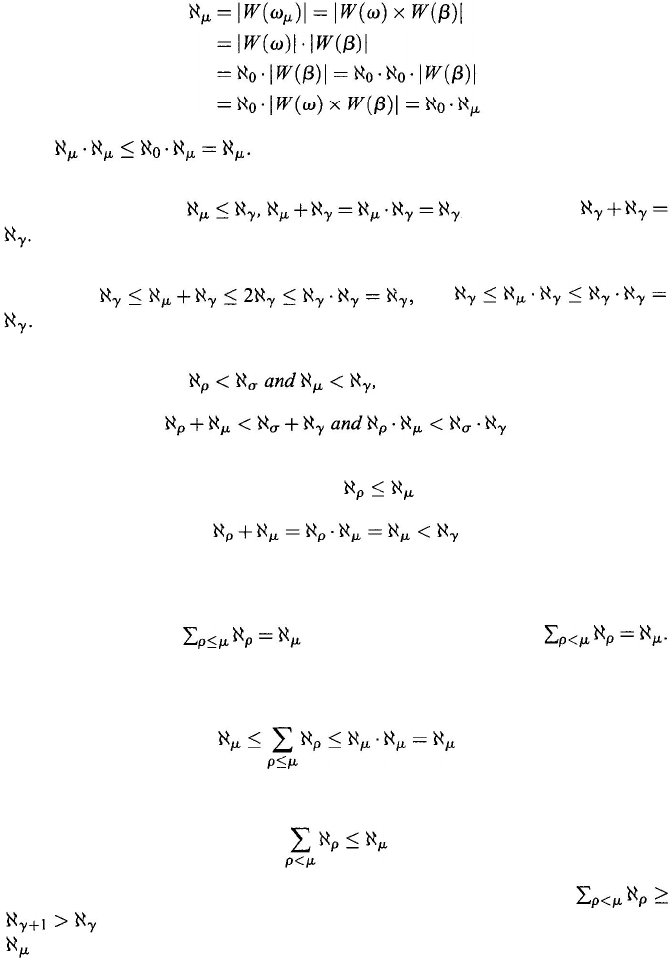
Naive Set Theory
55
where σ < ω. Therefore, when α is a limit number, we have α = ωβ. This implies
that
ω
µ
= ωβ for some fixed ordinal β. Therefore,
Thus,
Theorem 2.5.34. For
; in particular,
Proof:
and
Theorem 2.5.35. For
Proof: Without loss of generality, let . Then
Theorem 2.5.36. (1)
, and (2) if
µ
is a limit number,
Proof:
We have invariably
If µ is a limit number, then, on the one hand,
and, on the other hand, for every
γ < µ we also have γ + 1 < µ, so
; i.e., the sum is greater than every cardinal number which is less than
. These two results then yield the assertion in this case, too.

56
Chapter 2
Theorem 2.5.37. For ordinals γ and µ with µ ≤ γ + 1,
Proof: According to Theorem 2.3.9 and the hypothesis
and hence
Theorem 2.5.38.
The number class Q ordered according to increasing mag-
nitude of its elements, has order type ω
µ
+1
and therefore has cardinality
Proof: The elements of Q are the ordinal numbers γ with
(2.113)
Hence, in the sense of addition of well-ordered sets, we have
This implies that
From this we have
But Theorem 2.5.35 implies that we cannot
have
Let be the order type of Q Then Eq. (2.113) implies that
and
implies that
. Hence,
2.6.
Crises of Naive Set Theory
Careful readers may have already found some inconsistencies in the develop-
ment of naive set theory. These contradictions are connected with the following
concepts.

Naive Set Theory
57
(a) The set of all cardinal numbers. For example, let A be the set of all cardinal
numbers. Then Theorem 2.5.16 implies that there exists a cardinal number
greater than all numbers in A
. That is,
This contradicts Theorem
2.5.33.
(b)
The set of all ordinal numbers. For example, Theorem 2.5.16 implies that
to every set of ordinal numbers there exists a still greater ordinal number.
Accordingly, the concept of “set of all ordinal numbers” is a meaningless
concept. This is the so-called Burali-Forti paradox.
(c)
The set of all sets which do not contain themselves as elements
(Zermelo–Russell paradox or simply Russell’s paradox). For this set X, as
for every set, only the following two cases are conceivable: either X
contains itself as an element, or it does not. The first case cannot occur
because otherwise X would have an element, namely, X, which contained
itself as an element. The second assumption, however, also leads to a
contradiction. For in this case, X would be a set which did not contain
itself as an element, and for this very reason X would be contained in the
totality of all such sets, i.e., in X.
(d)
The set of all sets. For if X is such a set, it would have to contain the set of
all its subsets. The set of all subsets of X
, however, has a greater power
than X
, according to Theorem 2.1.4.
From the list of paradoxes above, we can see that two concepts, or words,
appear in each of them. One of the two words is “set” and the other is “all.” The
concept “set” was introduced by Cantor as “a collection into a whole of definite,
well-distinguished objects.” The meaning of this definition might be too wide for
us to avoid these paradoxes. The concept “all” actually was never introduced in
the context, and the meaning of “all” we have been using contradicts some results
we get in set theory. Our analysis on the appearance of the paradoxes shows that
if we can narrow the meaning of the concept of “set” and if we can avoid using the
word “all,” we may be in good shape to establish a set theory without contradictory
propositions. In the next chapter, we will try along this line to study properties of
abstract sets and to set up a new theory of sets, called the axiomatic set theory on
ZFC.
For further study of naive set theory, the reader is advised to consult
(Kuratowski and Mostowski, 1976).
CHAPTER 3
Axiomatic Set Theory
This chapter investigates how naive set theory can be rebuilt so that the resulting
set theory will not contain the paradoxes in Section 2.6. Axiomatic set theory,
based on the ZFC axiom system (i.e., Zermelo–Fränkel axioms and the Axiom of
Choice) is introduced.
In Section 3.1 we introduce the language of axiomatic set theory, list the
axioms of ZFC, and discuss some related philosophical problems. Section 3.2
sketches the development of the ordinal and cardinal number systems, based on
the axioms of ZFC, excluding regularity. Section 3.3 covers some special topics
in combinatorial set theory. Martin’s axiom (MA) is introduced to study some
related problems. Section 3.4 develops the class WF of all well-founded sets and
shows that all mathematics takes place within WF.
3.1. Some Philosophical Issues
Most scientific workers have little need for a precise codification of the concepts
of set theory. It is generally understood that some principles are correct and some
are questionable. In this chapter, we establish a set theory which makes more
precise the basic principles of naive set theory. To accomplish this, we build the
theory on a few axioms.
The idea of establishing a theory upon a set of axioms harks back to the
time of Euclid. Usually, in science, axioms, principles, and laws are stated in an
informal language, i.e., a language with many grammatical inconsistencies, such
as English. A major disadvantage of using an informal language is the possible
misunderstanding of a sentence or word. For example, in the past few decades,
the word “system” has been understood in many different ways (see Chapter 4
for a detailed discussion). In order to establish a rigorous set theory, we state our
axioms in a formal, or artificial, language, called first-order predicate calculus.
The characteristic of a formal language is that there are precise rules of formation
for linguistic objects.
59
