Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.


Naive Set Theory
39
also be a sequence of natural numbers, and with it we form the order type
Suppose that
α
= β. Then we are to show that the sequences (2.78) and (2.80)
coincide. This follows by induction from the following auxiliary consideration:
Let X
i
and Y
i
be distinct ordered sets, i = 1,2. Then the relations
(2.81)
follow from
(a)
have no first element, and
X
i
, i = 1,2, are
finite sets,
(b)
In fact, for the case (a), under a similarity mapping of
X
1
+ Y
1
onto X
2
+ Y
2
,
no element of Y
2
can correspond to an element of
X
1
because every element of X
1
is preceded by only a finite number of elements in
X
1
+ Y
l
, whereas every element
of Y
2
is preceded by infinitely many elements in
X
2
+ Y
2
. It follows, likewise, that
no element of Y
1
can correspond to an element of
X
2
. Consequently,
X
1
is mapped
on X
2
and Y
1
is mapped on Y
2
. In (b) under a similarity mapping of
Y
l
+ X
1
onto
Y
2
+ X
2
, an element
x
1
of X
1
cannot correspond to an element
y
2
of Y
2
; otherwise
the subset Y
1
preceding
x
1
in Y
1
+ X
1
would have to be mapped on a part
of
the elements of Y
2
, which is impossible, because Y
1
does not have a last element,
whereas
does. In like manner we see that no element of Y
1
can correspond to
an element of X
2
. Hence, also in this case, X
1
is mapped on X
2
and Y
1
is mapped
on
Y
2
.
If we now apply (a) to the equal sums α = β, we get
and
so that, by (b),
and hence, by (a),
etc. Thus, by induction it follows that the sequences (2.78) and (2.80) coincide.

40
Chapter 2
Since the totality of distinct sequences (2.78) gives rise to distinct order types
(2.79), and since (2.79) implies that any set with order type (2.79) has cardinality
has at least the power of the set of all sequences (2.78). The
power of these sequences of numbers is
A set A is densely ordered by an order relation < if < is linear and for any two
elements x and y
∈ A there exists an element z ∈ A between x and y. We say also
that A is dense. In a densely ordered set no element has either a direct successor
or a direct predecessor. An ordered set is called unbordered if it is not empty and
has no maximal or minimal elements.
All one-element sets, as well as the empty set, are densely ordered. All other
densely ordered sets contain infinitely many elements.
Theorem 2.4.5
[G. Cantor].
All unbordered, dense, denumerable sets are similar
to one another.
Proof:
Let
(X, ≤
X
)
and (Y, ≤
Y
)
be two sets of the kind mentioned in the
theorem. Since they are denumerable, they can be written as sequences
(2.82)
and
(2.83)
We now show that X and Y with their orders ≤
X
and ≤
Y
can be mapped onto
each other. To this end, let x
0
correspond to any element n
0
of
Y, say n
0
= y
0
.
We then look for the element in Y – {
n
0
} with the smallest index, denoted by n
1
,
such that
n
0
<
Y
n
1
when
x
0
<
X
x
1
, or
n
0
Y
>
n
1
when
x
0
X
> x
1
. This is possible
because Y is unbordered. We associate x
1
with
n
1
.
Now
x
2
may appear before, after, or between
x
0
and x
1
under
≤
X
. In each case,
since (Y, ≤
Y
) is unbordered and dense, there is an element n
2
with the smallest
index in sequence (2.83) which has the same position relative to n
0
and n
1
as x
2
has relative to
x
0
and x
1
.
In this way, a mapping h from X into Y is defined. In fact, h is onto. Suppose
that h is not onto; then Let yn be the first element in (2.83) such
that y
n
∈ Y – h
(
X
). Then there are three possibilities:
(1)
(2)
(3)
there are i, j < n such
that
and no other
y
k
, for k < n, is
between
y
i
and y
j
.
y
n
<
Y
y
i
,
for all
i < n.
y
n
Y
>
y
i
, for all i < n.

Naive Set Theory
41
If (1) is true, and since (
X, ≤
X
) is unbordered, it follows that there exists
x
∈
X
such that x <
X
h
–1
(
y
i
), i < n. Let x
m
be the first element in sequence (2.82)
such that
x
m
<
X
h
–1
(
y
i
), i < n. Then the definition of h implies that h
(
x
m
) = y
n
,
contradiction. A similar argument shows that (2) and (3) do not hold. Therefore,
h
is a similarity mapping from (
X, ≤
X
) onto (
Y, ≤
Y
).
The proof of Theorem 2.4.5 yields the following result, the proof of which is
left for the reader.
Theorem 2.4.6. Given any dense set with at least two elements and any linearly
ordered denumerable set, there is always a subset of the former which is similar
to the latter:
Let (
A, ≤
A
) be a linearly ordered set. A pair (
X, Y) is a cut in the ordered set
A, if
Y
=
{
a
∈
A : x ≤
A
a,
for all
x
∈
X
}
and
X
=
{
a
∈
A
:
y
A
≥
a
,
for all
y
∈
Y
}.
The set X is called the lower section, and Y the upper section, of the cut.
Proposition 2.4.3. Let (X, Y ) be a cut in a linearly ordered set A.
Then X ∩ Y
contains at most one element.
Proof: If there are x and y
∈ X ∩ Y , then it must be both x ≤ y and y ≤ x.
Thus, x = y.
A set A is continuously ordered if A is linearly ordered and each proper cut
(X, Y ) in A (i.e., X
≠≠ Y) has a nonempty intersection X ∩ Y. We also say that
A is continuous.
Theorem 2.4.7.
Every continuous set
(
A, ≤
A
) contains a subset which is similar
to the set of all real numbers in their natural order.
Proof:
According to Theorem 2.4.6, (
A, ≤
A
) contains a subset Q which is
similar to the set of all rational numbers. The set Q ordered by
≤
A
has gaps. In
other words, there is at least one proper cut (X, Y ) in (Q,
≤
Q
), where ≤
Q
is the
restriction of ≤
A
on the set
Q
, defined by
≤
Q
=
≤
A
∩
Q
², such that X ∩ Y =
Let
Q = X + Y
(2.84)
be a decomposition of Q where the cut (X, Y ) determines a gap in Q Then
(A,
≤
A
) contains an element a which succeeds all elements of X while preceding
all elements in Y. In fact, let X* be the totality of elements of A which belong to X
or precede an element of
X
, and let Y
* be the totality of elements of
A
which belong
to Y or succeed an element of Y. If (X*, Y*) is a cut with a gap, the set (A , ≤
A
)
would have a gap, contrary to the assumption that (A,
≤
A
) is continuous. Hence,
X* + Y * lacks at least one element a of A
, and, according to the construction of
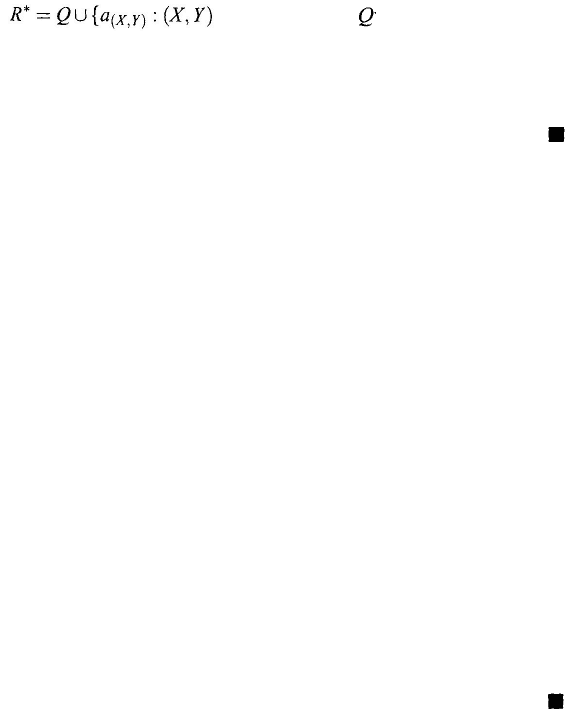
42
Chapter 2
X
*
+ Y
*
, this element succeeds X
*
and precedes Y
*
, so it also succeeds X and
precedes Y.
Every cut (2.84) thus determines at least one element a of A. For every gap
(2.84), we choose one of these elements a
(
X,Y
)
and keep it fixed. Let
is a proper cut in
with a gap}
This set is also ordered by ≤
A
and is similar to the set of all rational numbers
together with their gap elements in the domain of real numbers. In other words,
according to Dedekind’s introduction of the real numbers, R
*
is similar precisely
to the set of all real numbers, which proves the theorem.
Theorem 2.4.8. Let (
A,
≤
A
) be an ordered set with the following properties:
(1)
(
A,
≤
A
)
is unbordered.
(2)
(A, ≤
A
)
is continuous.
(3)
(A, ≤
A
) contains a denumerable set U such that between every pair of
elements of A there exists at least one element of U.
Then (A,
≤
A
) is similar to the naturally ordered set of all real numbers.
Proof: The set U is unbordered, because before and after every element of U
there are still elements of A, and hence, due to (3), elements of U. Likewise, it
follows from (2) and (3) that U is dense also. Consequently, U is similar to the set
of all rational numbers ordered naturally. Every gap in U determines, according
to the proof of Theorem 2.4.7, at least one element a of A and, because of (3), not
more than one element of A. This, however, implies the assertion. For the set of
all rational numbers can be mapped on U, whereby with every gap in the domain
of rational numbers there is associated precisely one gap of U and, consequently,
precisely one element of A. We have thus obtained a similarity mapping of the set
of all real numbers on the set A.
2.5.
Well-Ordered Sets
An ordered set (
X,
≤
X
) is well-ordered if it is linearly ordered and every
nonempty subset of X contains a first element with respect to the relation
≤
X
.

Naive Set Theory
43
Example 2.5.1. Every finite linearly ordered set is well-ordered and so is the set
= {0,1,2,3,...}. The set {...,3,2,1,0} is not well-ordered because it does
not have a first element. The set of all real numbers in the interval [0,1], in their
natural order, is not well-ordered because the subset (0, 1] does not have a first
element.
The following two theorems are simple consequences of the definition.
Theorem 2.5.1. In every well-ordered set there exists a first element. Every
element except the last element (if such exists) has a direct successor.
Theorem 2.5.2. No subset of a well-ordered set is of type
*
ω.
Theorem 2.5.3.
If a linearly ordered set A is not well-ordered, it contains a subset
of type
*
ω.
Proof: Let P be a nonempty subset of A which contains no first element. Let
(2.85)
We have for every x
∈ P. Let p
0
be any element in P. We define by
induction a sequence
by letting
Since
p
n
< p
n –1
, for n > 1, this sequence is of type
*
ω.
Theorems 2.5.2 and 2.5.3 imply the next results.
Theorem 2.5.4.
In order that a linearly ordered set be well-ordered, it is necessary
and sufficient that it contain no subset of type
*
ω.
Theorem 2.5.5 [Principle of transfinite induction]. If a set A is well-ordered,
B
⊂ A, and if for every x ∈ A the set B satisfies the condition
(2.86)
then B = A.
Proof: Suppose that
Then there exists a first element in A – B.
This means that if y < x, then y
∈ B. This shows that {y ∈ A : y < x} ⊂ B. Now
it follows from (2.86) that x
∈ B, which contradicts the hypothesis that x ∉ B.
Let (
A,
≤
) be a linearly ordered set. A function f : A → A is an increasing
function if f satisfies the condition
(2.87)

44
Chapter 2
Theorem 2.5.6. If a function f : A → A is increasing, where (A, ≤
A
) is a well-
ordered set, then for every x
∈ A we have x ≤
A
f (x).
Proof: Let We
now show that
x
∈
B.
In fact, let
y
∈
O
(x); that is, y <
A
x. By (2.87) it follows that
Since
y
∈
B,
we have
y
≤
A
f
(
y
) and thus
y
<
A
f
(
x). This means that
the element f (x) occurs after every element y of O(x ), that is, f
(
x )
∈ A – O(x
).
Since x is the first element of A – O
(
x), we have x ≤
A
f (x ) and finally x ∈ B.
Hence, from Theorem 2.5.4 the set B equals A.
Corollary 2.5.1. If the well-ordered sets A and B are similar, then there exists
only one similarity mapping from A onto B.
Proof:
Suppose that the sets A and B are well ordered by ≤
A
and ≤
B
and that
there exist two functions f and g establishing similarity from A onto B.
The function
is clearly increasing in A. By Theorem 2.5.5 we thus
have
for every x
∈ A. Hence, g
(
x ) ≤ B f
(
x). Consequently,
instead of By the same argument f
(
x )
≤
B
g
(
x ). This implies
Corollary 2.5.2. No well-ordered set is similar to any of its initial segments.
Proof:
Let x ∈ A, where (
A,
≤
A
) is a well-ordered set. The initial segment
is the set defined by
(2.88)
Suppose that A and are similar. Then the function f establishing the
similarity from A onto would be increasing and would satisfy f(x
)
∈
that is, f
(
x) <
A
x. But this contradicts Theorem 2.5.5.
Theorem 2.5.7. Let A and B be two well-ordered sets. Then,
(i)
A and B are similar, or
(ii)
A is similar to a segment of B, or
(iii)
B is similar to a segment of A.

Naive Set Theory 45
Proof:
Let ≤
A
and ≤
B
be relations which well-order A and B, respectively,
and let
(2.89)
By Corollary 2.5.2, for given x
∈ Z there exists only one segment such
that Let a function f : A
→ B be defined by f
(
x) = y for each
x
∈ A, such that
First we show that either Z = A or Z is a segment of A that is, there exists an
a
∈ A such that In fact, let
Since
is a segment
of the function f also maps onto a segment of B. Hence, x
∈ Z.
Similarly, either
f
(Z) = B or else f
(
Z ) is a segment of B :
To
show this it suffices to observe that
(2.90)
Finally, we observe that f establishes the similarity between Z and f(Z).
Indeed, we have just shown that x < x'
∈ Z implies that is a segment
of therefore, f (x ) < f (x
).
Therefore, we have one of the following four possibilities:
The first three possibilities correspond to those stated in the theorem. Case (4)
is impossible, because then
and, thus, by definition of
Z, a
∈
Z
;
that is,
which contradicts the definition of a segment.
Corollary 2.5.3. If A and B are well-ordered, then |A|
≤ | B |or |B| ≤ |A |.
By ordinal numbers (or ordinals or ordinalities) we understand the order types
of well-ordered sets. Theorem 2.5.7 implies that we can define a “less than”
relation for ordinals. We say that an ordinal
α is less than an ordinal β if any set
of type
α is similar to a segment of a set of type β. This relation will be denoted
α < β or β > α. We write α ≤ β instead of α < β or α = β.
Theorem 2.5.8. For any ordinals α and β one and only one of the following
formulas holds:
(2.91)

46
This theorem is a direct consequence of Theorem 2.5.7.
Theorem 2.5.9.
If α, β, and γ are ordinals such that α < β and β < γ, then
α < γ.
Proof:
Let A, B, and C be well-ordered sets of types α, β, γ, respectively.
By assumption, A is similar to a segment of B and B is similar to a segment of C.
Thus, A is similar to a segment of C.
The following formulas can be proved without difficulty:
Theorem 2.5.10.
If the well-ordered sets A and B are of types α and β and if A is
similar to a subset of B, then
α ≤ β.
Proof:
Let h : A → B be a mapping such that h establishes the similarity
between A and h
(
A). If the theorem were not true, then we would have β < α and
then B would be similar to a segment of h
(
A). This contradicts Theorem 2.5.5.
Theorem 2.5.11.
The set W (α) consisting of all ordinals less than α is well-
ordered by the relation
≤. Moreover, the type of W (α
)
is
α.
Proof:
Let A be a well-ordered set of type α. Associating the type of the
segment
O
(
a
) with the element a ∈ A, we obtain a one-to-one mapping of A onto
W
(
α). It is easily seen that the following conditions are equivalent:
(1)
a
1
precedes
a
2
or a
1
= a
2
.
(2)
O(a
1
) is a segment of O(
a
2
) or O
(
a
1
) = O (
a
2
).
(3)
The type of
O
(
a
1
) is not greater than the type of O(
a
2
).
This shows that the relation
≤ indeed orders W (
α
) in type α.
Theorem 2.5.12.
Every nonempty set of ordinals has a first element under the
relation
≤.
Proof:
Let A be a nonempty set of ordinals and α ∈ A. If α is not the smallest
ordinal of
A,
then
A
∩
W
(
α
) ≠
Then in the set
A
∩
W
(
α
) there exists a smallest
number β because W(α) is well-ordered. At the same time, β is the smallest
ordinal in A.
Chapter 2

Naive Set Theory
47
An ordinal number is a limit ordinal if it has no direct predecessor. All order
types of finite well-ordered sets are denoted by the corresponding natural numbers.
For example,
{0} = 1,
{0,1}
=2,
{0,1,2,} = 3,....
Then the order type 0 of the
empty set is a limit ordinal.
Theorem 2.5.13. Each ordinal can be represented in the form
λ + n, where λ is a
limit ordinal and n is finite ordinal (natural number).
Proof: Let
α be an ordinal and A a set of type α. Every set of the form
A – O(
a
) is a remainder of A. Clearly,
A
–
O
(
a
1
) ⊂ A
–
O
(
a
2
)
if and only if
(a
1
≥ a
2
)
(2.92)
This implies that there exists no infinite increasing sequence of distinct remainders.
So there exists only a finite number of m ∈ such that there exists a remainder of
power m. If n is the greatest such number and if A – O(
a
) is a remainder of power
n
, then the segment O(
a
) has no last element. Thus O(
a
) is a limit ordinal λ. This
implies that
α = λ + n.
Let
α
be an ordinal number. A transfinite sequence of type
α
(or an
α
-sequence)
is a function
ϕ
whose domain is
W
(α). If the values of ϕ are ordinals, the sequence
is also called a sequence of ordinal numbers. In particular, an
α-sequence ϕ of
ordinals will be called an increasing sequence if for any µ,
γ ∈ W (α), µ < γ
always implies ϕ(µ) < ϕ(γ); it is a decreasing sequence, if µ < γ invariably
implies
ϕ
(µ )>ϕ(γ).
Theorem 2.5.14. Every set of ordinal numbers can be written as an increasing
sequence.
This is a consequence of Theorem 2.5.12.
Theorem 2.5.15. Every decreasing sequence of ordinal numbers contains only a
finite number of ordinal numbers.
This result follows from Theorem 2.5.12.
Theorem 2.5.16.
To every set M of ordinal numbers µ, there is an ordinal number
which is greater than every ordinal number µ in M.
Proof: By Theorem 2.5.14, we can assume that M is an increasing sequence.
Let
M*=
{
µ +1:µ
∈
M} and σ =
U
{W(µ +2):µ ∈ M}.
Then every µ +1
≤
σ
; hence, µ < σ, for every µ ∈ M.
Let
ϕ
be a
λ-sequence of ordinals where λ is a limit ordinal. By Theorem
2.5.16 there exist ordinals greater than all ordinals
ϕ
(γ) where γ < λ. The smallest
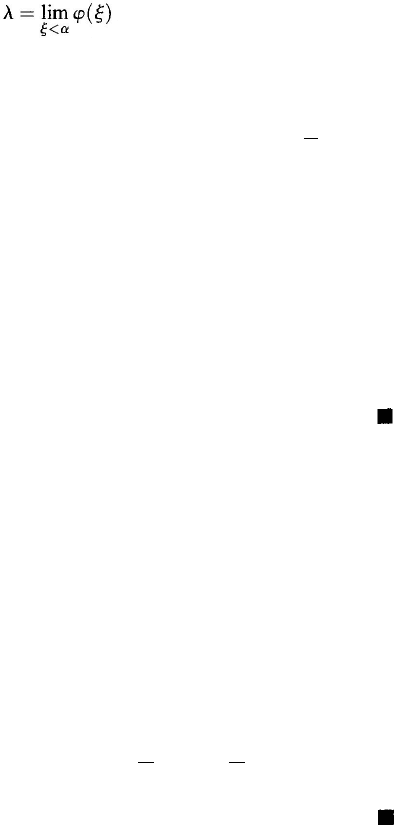
48
Chapter 2
such ordinal (see Theorem 2.5.12) is called the limit of the λ-sequence ϕ(γ) for
γ < λ
and is denoted by lim
γ<λ
ϕ(γ).
We say that an ordinal
λ
is cofinal with a limit ordinal α if λ is the limit of an
increasing
α
-sequence
(2.93)
Theorem 2.5.17. An ordinal
λ is cofinal with the limit ordinal α if and only if
W(
λ) contains a subset of type α cofinal with W(λ).
Proof: Let A be a subset of W(
λ
) cofinal with
W
(λ) and such that A = α. For
every ordinal
ξ < α there exists an ordinal ϕ(
ξ
) in A such that the set {η ∈ A :
η < ϕ(
ξ
)
} is of type ξ. The sequence ϕ(
ξ
) is clearly increasing and ϕ
(
ξ
) < λ for
ξ < α because ϕ(
ξ
) ∈ A ⊂ W(λ). If µ < λ, there exists an ordinal ξ < λ such that
µ <
ξ because the sets A and W (λ) are cofinal. Thus, µ < ξ ≤ ϕ(
η
) for some
η < α. This shows that λ is the least ordinal greater than all ordinals ϕ(ξ), ξ < α
,
which proves Eq. (2.93).
Suppose, in turn, that Eq. (2.93) holds. Let A be the set of all values of ϕ.
We have η < λ for all η ∈ A and, consequently, since λ is a limit ordinal, there
exists
ξ ∈ W(λ) such that η < ξ. Conversely, if ξ ∈ W(λ) then ξ < λ, and by the
definition of limit there exists
ξ′ < α such that ξ < ϕ(ξ′). This means that some
ordinal in A is greater than
ξ. Hence, the sets A and W(λ
) are cofinal.
We now consider the arithmetic of ordinal numbers.
Theorem 2.5.18. The sum and product of two ordinal numbers are ordinal num-
bers.
Theorem 2.5.19.
The ordered sum of ordinal numbers, where the index set is also
well-ordered, is an ordinal number.
These theorems are consequences of the definitions in the previous section.
Theorem 2.5.20 [The First Monotonic Law for Addition].
(
α< β ) →( γ + α< γ + β )
(2.94)
Proof: Let B and C be disjoint sets such that B =
β and C = γ. Since α < β,
B contains a segment A of type α. The ordered sum C + A, which is of type γ + α,
is a segment of C + B, which is of type γ + β. Thus, γ + α < γ + β.
Theorem 2.5.21 [The Second Monotonic Law for Addition].
(
α≤β) →( α+γ≤β+γ
)
(2.95)
