Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.

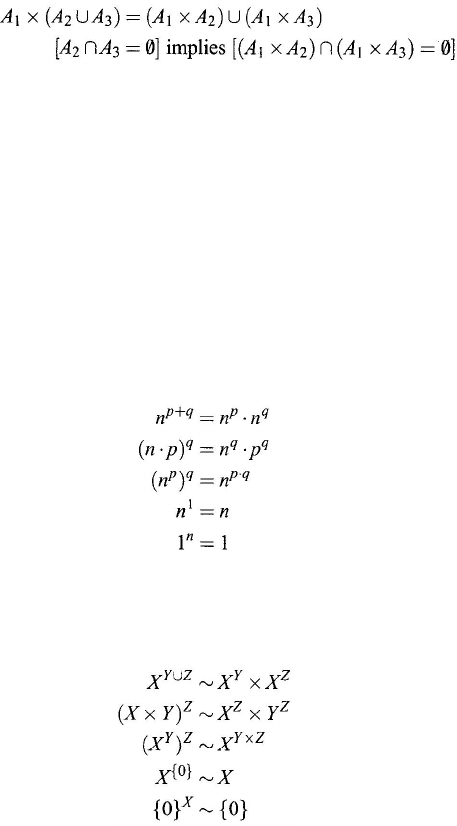
Naive Set Theory
29
Equation (2.38) is shown by the following:
Denote the
n
-fold product m ⋅ m ⋅ ⋅ ⋅ m by m
n
.
Then
m
n
is the power of the set
of all sequences of
n
-elements (
a
1
,
a
2
, . . . ,a
n
), where
a
1
, . . . , a
n
are elements of a
set A of power m. In other words,
⏐A⏐
n
=
⏐
A
n
⏐
. Generalizing this idea, let m, n,
and p be cardinal numbers. Then
(read as m equals n raised to the pth power) if every set of power m is equipollent
m = n
p
(2.39)
to the set A
B
, where
⏐
A
⏐
=
n,
⏐
B⏐
=
p,
and
A
B
= {
ƒ :
ƒ is a function from B into A}.
Theorem 2.3.8. For arbitrary cardinal numbers n, p, and q,
(2.40)
(2.41)
(2.42)
(2.43)
(2.44)
Proof: Suppose that X, Y, and Z are pairwise disjoint sets with
⏐X⏐ = n,
⏐ Y⏐ = p, and ⏐Z
⏐
=
q.
Then, showing Eq. (2.40)–(2.44) is equivalent to showing
(2.45)
(2.46)
(2.47)
(2.48)
(2.49)
The proofs of Eqs. (2.48) and (2.49) are straightforward. We give only the
arguments of the important formulas Eqs. (2.45)–(2.47).
To prove Eq. (2.45), we associate with every function ƒ
∈ X
Y
∪
Z
the ordered
pair of restricted functions (ƒ
⏐
Y, ƒ
⏐
Z
). Then it is not difficult to show that this
correspondence is a bijection from the set
X
Y
∪
Z
onto the set X
Y
× X
Z
.
For the proof of Eq. (2.46), notice that if ƒ ∈ (X × Y
)
Z
, then ƒ (
z
) is, for every
z ∈ Z, an ordered pair (
g
(
z), h
(
z
)), where
g
(
z) ∈ X and h
(z
) ∈ Y. Then g ∈ X
Z
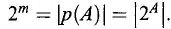
30
Chapter 2
and h ∈ Y
Z
. It is easy to show that this correspondence of the function ƒ to the
pair (
g, h
) determines a l–l mapping from the set (
X × Y
)
Z
onto the set X
Z
× Y
Z
.
Finally, let us prove Eq. (2.47).
Let ƒ
∈ X
Y
∪
Z
; hence ƒ is a function of
two variables y and z, where y ranges through the set Y and z through the set
Z and where ƒ takes values in X. For each fixed z, the function g
z
defined by
g
z
(y
) = ƒ(
y,z) is a function from Y into Y; i.e., g
z
∈ X
Y
. The function F defined
by F
(
z) = g
z
associates with every z ∈ Z an element of the set X
Y
, so
F
∈
(
X
Y
)
Z
.
If ƒ
1
and ƒ
2
are distinct functions from X
Y
∪
Z
, then the corresponding functions
F
1
and F
2
are also distinct. In fact, if ƒ
1
(y
0
, z
0
) ≠ ƒ
2
(
y
0
, z
0
), then the elements
F
1
(z
0
) and F
2
(
z
0
) of X
Y
are distinct. Each function F ∈ (X
Y
)
Z
corresponds in
a manner described before to some function ƒ
∈ X
Y
×
Z
, namely, ƒ
(
y,z) = g
z
(
y),
where
g
z
= F(
z
). It follows that the correspondence of the function ƒ ∈ X
Y
×
Z
to
the function F
∈ (X
Y
)
Z
establishes the equipollence set
X
Y × Z
with (
X
Y
)
Z
, which
proves Eq. (2.47).
Theorem 2.3.9.
If A has the power m, then the power set p
(
A
) has power 2
m
; i.e.,
Proof: By definition, 2
m
is the power of the set {0, 1}
A
, consisting of all
functions ƒ whose values are the numbers 0 and 1 and whose domain is the set
A. Each such function is uniquely determined by the set X
ƒ
of those a ∈ A for
which ƒ(
a
) =
1. To distinct functions ƒ
1
and ƒ
2
correspond distinct sets
X
ƒ
1
and
X
ƒ
2
. Thus, associating with the function ƒ ∈ {0, 1}
A
the set Xƒ ⊂ A, we obtain a
bijection from the set {0, 1}
A
onto the set
p
(
A
).
Theorem 2.3.10. The relation “≤ ” between cardinal numbers possesses the fol-
lowing properties:
m
≤ n and n ≤ p
imply
m ≤ p
(2.50)
m
≤ n
implies
m + p ≤ n + p
(2.51)
m ≤ n implies
mp
≤ np
(2.52)
m
≤ n
implies
m
p
≤ n
p
(2.53)
m
≤ n implies
p
m
≤ p
n
(2.54)
Proof: Equation (2.50) expresses the transitivity of the relation
≤. Equations
(2.51)–(2.54) express the monotonicity of addition, multiplication and exponenti-
ation with respect to
≤. The proof is straightforward and is omitted here.
In the arithmetic of natural numbers, the laws converse to Eqs. (2.51)–(2.54)
are called the cancellation laws for the relation
≤ with respect to the operations of
Naive Set Theory
31
addition, multiplication, and exponentiation. These theorems hold in arithmetic
provided that p > 1. In the arithmetic of arbitrary cardinal numbers all of the
cancellation laws fail to fold: it suffices to let m = 2, n = 3, and p =
ℵ
0
to obtain a
counterexample. On the other hand, the cancellation laws with respect to addition,
multiplication, and exponentiation hold for the relation <. They follow without
difficulty from the law of trichotomy, which now we state without proof.
Theorem 2.3.11. For arbitrary cardinal numbers m and n, either m ≤ n or n ≤ m.
We now study a few properties of the cardinal numbers
ℵ
0
and c.
(1) c =c+c
:
In fact, let X and Y be intervals (0,1) and [1,2). Then ⏐X
⏐
=
⏐
Y
⏐
=
c
and
⏐
X
∪
Y⏐ = c + c = ⏐
(0,2)
⏐
= c.
(2)
For each natural number
n, n
<
ℵ
0
< c
:
The inequality follows from Theorem 2.1.3.
(3)
For each natural number n, n + c = ℵ
0
+ c = c
:
In fact, c ≤ n + c ≤ ℵ
0
+ c ≤ c + c = c. So, by property 1 and Bernstein’s
theorem, the result follows.
(4)
c = c
·
c
:
Proof: Let X be the set of all points in (0,1]. Then X × X = {(x,y) : x,y ∈
(0, 1]} has power c · c. The assertion is proved as soon as we show that the
sets X and X × X are equipollent.
Let z
∈ (0,1) and (x,y) ∈ X × X.
We write the numbers x, y and z by
nonterminating decimal fractions. Since the representation of our numbers
by means of such decimal fractions is unique, it is necessary to show that
the set of decimal fraction pairs
x, y can be mapped on the set of decimal
fractions
z.
Let the pair of decimal fractions
x
and
y
be given. Now we write
the first x-complex, then the first y-complex, then the second x
-complex,
followed by the second y-complex, etc. Since neither x nor y exhibits only
zeros from a certain point on, the process can be continued without ending
and gives rise to a nonterminating decimal fraction. This decimal fraction
shall be made to correspond to the number pair x,y. Every number pair x,y
thus determines precisely one z; conversely, every z determines exactly one
number pair x,y, and, in fact, precisely that pair which gave rise to z. A
one-to-one correspondence between the number pairs x,y and the numbers
z is thereby established, and this completes the proof.
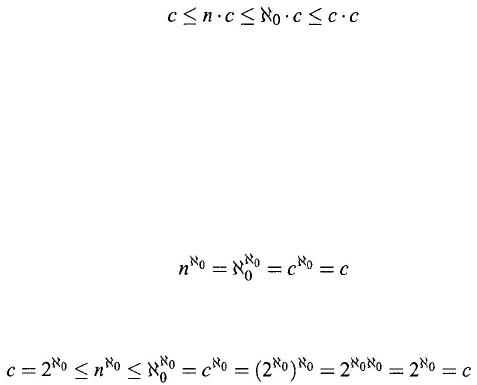
32
(5)
For each natural number n, n ⋅ c = ℵ
0
⋅ c = c
:
In fact, from Theorem 2.3.10, we have
Chapter 2
(2.55)
Thus, it follows from Bernstein’s theorem and property 4 that
n
⋅ c= ℵ
0
⋅ c = c.
(6) For each natural number n, c
n
= c:
By induction and property 4 we obtain the proof.
(7)
Under the hypothesis that c = 2
ℵ
0
, this is the continuum hypothesis. We
have the following: for each natural number n > 1,
(2.56)
In fact, from Theorem 2.3.10, it follows that
whence property 7 follows by applying Bernstein’s theorem.
2.4. Ordered Sets
Since the elements of sets need by no means be numbers or points on the real
number line, and even if the elements are numbers, it is not at all necessary for
them to be ordered according to magnitude. The concept of ordered sets will be
formulated abstractly as follows:
A set
X
is called an ordered set if a binary relation, called an order relation and
denoted by ≤, exists with its field X such that
(1) For all x
∈ X, x = x.
(2) For x,y
∈ X, if x ≤ y and y ≤ x, then x = y ; i.e., the relation is
antisymmetric.
(3) For x,y,z
∈ X, if x ≤ y and y ≤ z, then x ≤ z ; i.e., the relation is transitive.
The ordered set X will be denoted by the ordered pair (X,
≤ ).
The notation x > y means the same as y < x and is read either “y precedes x”
or “x succeeds y.” The field of the order relation
≤ is often said to be ordered
without explicitly mentioning
≤. It is necessary to remember that an ordering is

Naive Set Theory
33
by no means an intrinsic property of the set. The same set may be ordered by
many different order relations.
Let X be a set ordered by a relation
≤. If x and y are elements of X and either
x
≤ y or y ≤ x, then we say that the elements x and y are comparable; otherwise
they are incomparable. If Y
⊂ X and any two elements of Y are comparable, then
we call Y a chain in X; if any two elements of Y are incomparable, then Y is called
an antichain in X. An order relation
≤ of a set X is called a linear order relation if
X ordered by
≤ becomes a chain.
Example 2.4.1.
(1)
Every family of sets is ordered by the inclusion relation.
(2)
The set of natural numbers is ordered by the relation of divisibility.
(3)
The set of natural numbers in the order indicated by {0,2,4, . . . , 1,3,5, . . . }
is a linearly ordered set; i.e., first come the even nonnegative integers
ordered according to increasing magnitude, and then the odd integers.
(4) The set {0, 2, 4, 6, . . . ,7, 5, 3, 1}, as written, is linearly ordered; that is, first
come the even nonnegative integers ordered according to increasing
magnitude, then the odd integers ordered according to decreasing
magnitude.
The next result is obvious.
Proposition 2.4.1. Let X be an ordered set with ordering
≤. Then every subset of
X is also ordered by
≤. Hence, the subsets of ordered sets can always be regarded
as ordered.
Two ordered sets (
X, ≤
X
) and (Y, ≤
Y
) are equal,
(2.57)
if X = Y and for any x, y ∈ X, x ≤
X
y is equivalent to x ≤
Y
y . Without confusion,
we write X =
Y instead. Thus, the sets in Examples 2.4.1(3) and 2.4.1(4) are to
be considered distinct in the sense of ordered sets. Without regard to an order,
however, the two sets are identical.
Let (X,
≤ ) be an ordered set and a ∈ X. The element a is called a maximal
(respectively, minimal) element in the ordered set X provided that no element
x
∈ X satisfies x > a (respectively, x < a ). The element a is called the maxi-
mum (respectively, minimum) element of X provided that for every x
∈ X, x ≤ a
(respectively, a
≤ x).
Proposition 2.4.2. An ordered set contains at most one maximum element and at
most one minimum element.

34
(1)
i.e., every ordered set is similar to itself.
(2)
implies
(3)
If
and
then
(4)
implies X ~ Y.
Chapter 2
Proof: Let a and a
*
be two maximum elements of a set ordered by an ordering
≤. Then a
*
≤ a and a ≤ a
*
, which implies that a = a
*
. The same argument shows
that an ordered set contains at most one minimum element.
An ordered set, however, need have neither a maximum nor a minimum ele-
ment.
An ordered set A is cofinal with its subset B if for every x
∈ A there exists
y
∈ B such that x ≤ y. The subset B is a cofinal subset in A. Analogously, we can
define coinitial sets and subsets.
Example 2.4.2. The set of all real numbers is cofinal and coinitial with the set of
all integers.
An ordered set (X,
≤
X
) is similar to an ordered set (Y, ≤
Y
),
(2.58)
if there exists a bijection h : X → Y such that for any x
1
,
x
2
∈ X, x
1
≤
X
x
2
implies
h
(x
1
) ≤
Y
h
(
x
2
). Without causing confusion, we write
XY
instead of Eq. (2.58).
The bijection h is called a similarity mapping from the ordered set (X, ≤
X
) onto
the ordered set (Y, ≤
Y
).
The following four fundamental properties result immediately from the defi-
nition:
Theorem 2.4.1. If a set X is equipollent to an ordered set (Y,≤
Y
), then X can be
ordered in such a way that X (Y,
≤
Y
).
Proof: Let h be a bijection from X onto Y. We define an order relation
≤
X
on
X as follows: For any if and only if
Theorem 2.4.2.
If two ordered sets are similar, then both possess maximum (min-
imum) elements or neither set has such an element.
Proof: Let (X,
≤
X
) and (Y, ≤
Y
) be two similar ordered sets with a similarity
mapping h : X
→ Y. If x
0
is a minimum element from X, then for every x ∈ X,

Naive Set Theory
35
This implies that for every
also has a minimum element.
The family of all ordered sets is divided, by similarity relation, into pairwise
disjoint groups, each of which contains all sets similar to each other. Two ordered
sets (
X, ≤
X
) and (Y, ≤
Y
) are of the same order type if they are similar. Each order
type will be denoted by a small Greek letter, and the order type of (X,
≤
X
) will
also be denoted by
without confusion.
The order type of the set of natural numbers, ordered according to increasing
magnitude, is denoted by
ω. If, on the other hand, these numbers are ordered
according to decreasing magnitude, then the order type of the set is denoted by
*
ω. Generally,
*
µ denotes that order type which results from µ when the order of
succession of the elements is reversed; i.e., when a new order relation is derived
from the relation < defined for the original set, by setting
*
< equal to >.
Let (X,
≤
X
) and (
Y,
≤
Y
) be two disjoint ordered sets. An order relation ≤ on
the union X
∪ Y is defined as follows: For any s
1
and
s
2
∈
X
∪
Y,
if
s
1
and
s
2
∈ X,
we let s
1
≤ s
2
if and only if s
1
≤
X
s
2
; if s
1
and s
2
∈ Y, we let s
1
≤ s
2
if and only
if s
1
≤
Y
s
2
; if s
1
∈ X and s
2
∈ Y, then we let s
1
≤ s
2
. The order relation ≤ thus
defined on the union is obviously transitive, and it therefore orders X
∪ Y. The
ordered sum X + Y of the ordered sets (X,
≤
X
) and (
Y,
≤
Y
) is now understood to
be the ordered set (
X
∪
Y,
≤ ).
Let
µ and γ be two order types and (X,≤
X
) and (Y,≤
Y
) be two disjoint
ordered sets such that
= µ and
= γ. The sum of the order types µ and γ is
defined by
(2.59)
It is again easy to see that the sum
µ + γ is independent of the choice of the
ordered sets (X,
≤
X
) and (Y, ≤
Y
).
The addition of order types need not be commutative. For example, if
X= {1, 2, 3, . . . } and Y = {0}
(2.60)
then
X + Y = {1, 2, 3, . . . ,0} and Y + X = {0, 1, 2, 3, . . . }
(2.61)
so that 1 +
ω = ω, but ω + 1 ≠ ω, where 1 is the order type of Y.
The associative law of order types
µ , γ, and π is valid:
(2.62)
The concept of addition of order types can be defined for arbitrary many
order types. In fact, let an ordered set (I,
≤
I
) be given, and to each k ∈ I there
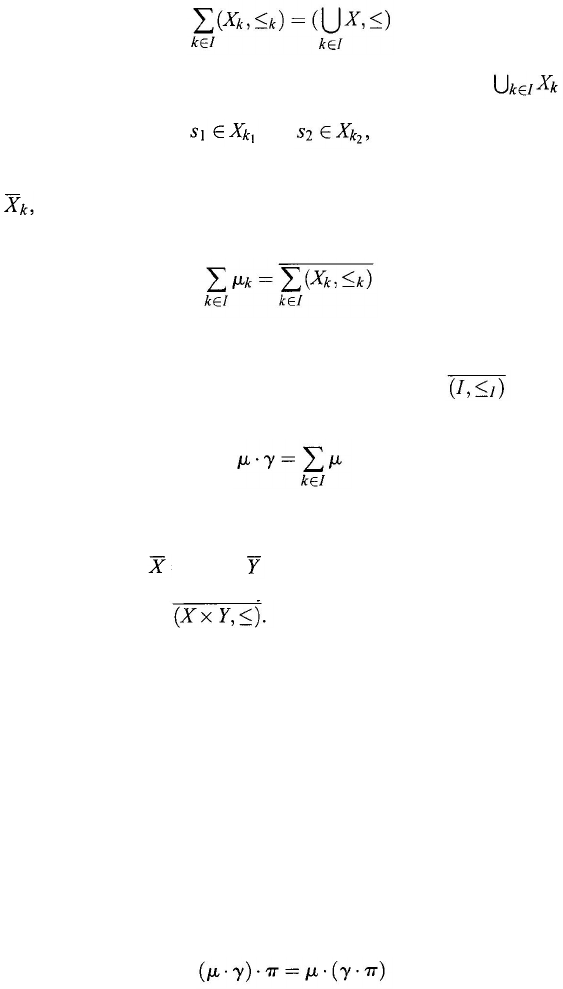
36
Chapter 2
corresponds an ordered set (X
k
,
≤
k
), where the sets X
k
are pairwise disjoint. Then
the ordered sum
(2.63)
is ordered in the following manner: If two elements s
1
and
s
2
of belong
to the same X
k
, then we let s
1
≤ s
2
if and only if s
1
≤
k
s
2
; if, however, s
1
and
s
2
belong to different X
k
’s, say
and then we let s
1
< s
2
if and only
if k
1
< k
2
.
Let
µ
k
be an order type for each k ∈ I and (X
k
, ≤
k
) an ordered set such that
µ
k
=
where {X
k
: k ∈ I) consists of pairwise disjoint sets. The sum of the
order types
µ
k
is defined by
(2.64)
It is easy to see once more that this sum is independent of the choice of the ordered
sets (X
k
,
≤
k
) .
In the previous definition, if µ
k
= µ for each k ∈ I and
=
γ, then the
product of the order types
µ ⋅ γ will equal the sum thus determined; i.e.,
(2.65)
For
γ = 0 we let µ ⋅ γ = 0. The concept of product of order types can also be
defined as follows: Let
K and µ be two ordered types of nonempty sets (X, ≤
X
)
and (Y, ≤
Y
) such that = K and
=
µ . Define an ordered set (X × Y, ≤) by
letting (x
1
,y
1
) < (x
2
,
y
2
) if and only if x
1
< x
2
, or when x
1
= x
2
then y
l
< y
2
.
Then the product µ ⋅ K =
The order relation defined here is called a
lexicographical order.
This second definition follows immediately from the first. It is also evident
from the second definition that the product of order types is independent of their
particular set representatives.
For multiplication there is no commutative law either. For if we choose
K = ω
and µ = 2, where 2 is the order type of { 0, 1 } ordered by 0 < 1, then 2 ⋅ ω = ω
and ω ⋅ 2 is the order type of the ordered set
{1, 3, 5, . . . ; 2, 4, 6, . . . }
(2.66)
This set is not certainly similar to any ordered set of type w. Hence, 2 ⋅ ω ≠ ω ⋅ 2.
We do have, however, for multiplication, as for addition, the associative law,
which is so important for calculation:
(2.67)

Naive Set Theory
37
In fact, let (X
,
≤
X
), (
Y
,
≤
Y
),
and (Z
,
≤
Z
) be ordered sets such that = µ ,
=
γ
, and
=
π .
Then, according to the second definition, the order type
(µ ·
γ) · π is the order type of the ordered set
(
Z
×
(
Y
×
X ), ≤
1
), where for any
(z
i
,(y
i
,x
i
)) ∈ Z ×(Y × X ),i = 1,2,
(2.68)
if
z
1
<
z
2
, or z
1
=
z
2
, y
1
<
y
2
, or z
1
=
z
2
and
y
1
=
y
2
and
x
1
< x
2
.
Likewise,
µ · (
γ · π) is the order type of the ordered set ((
Z × Y )×X,
≤
2
), where for any
((
z
i
,y
i
),x
i
)
∈
( Z ×Y )×X, i = 1,2,
(2.69)
if
z
1
<
z
2
,
or z
1
=
z
2
,
y
1
<
y
2
,
or
z
1
=
z
2
,
y
1
=
y
2
,
x
1
<
x
2
. If we now associate, for
the same elements x, y, and z, the element (z, (y
,
x)) with the element ((z
,
y
),
x
),
we define a similarity correspondence between
(
Z
×
(
Y
×
X
),
≤
1
)
and
((
Z × Y )×
X,
≤
2
). This proves the assertion.
The right distributive law does not hold. Namely,
(2.70)
For example,
and this differs from
(2.71)
(2.72)
The left distributive law, however, is valid; that is,
(2.73)
In fact, let (X, ≤
X
), (Y, ≤
Y
),
and (Z, ≤
Z
) be disjoint ordered sets such that
=
µ
,
= γ
, and
=
π
. Then π · (µ + γ) is the order type of the ordered set
where for any (
q
i
,
z
i
)
(2.74)
38
Chapter 2
Now it is evident that the same ordered set is obtained with order type π · µ +
π · γ
. This completes the proof of the statement.
It does not yet follow from the results derived thus far that to every cardinal
number
there corresponds at least one order type
µ
with
⏐
µ
⏐ =
where
⏐
µ
⏐
means the cardinality of any of those ordered sets with type µ. In other words, it
does not follow from the results derived that every set can be ordered. Let
be
the set of all order types which belong to a given cardinal number and call this
set the type class belonging to
Theorem 2.4.3. For any cardinal number
the type class
satisfies
(2.75)
Proof: Let X be a set with cardinality
Let
µ
be any order type in Then
it is always possible to order X so that = µ. The set of all order types of class
is equipollent to the set of all possible orderings of our set X. For each order
relation < on the set X, let S
<
= {(x
1
, x
2
) ∈ X² : x
1
< x
2
}. Then it can be seen
that different order relations <
1
and <
2
on X correspond to different subsets S<
1
and S<
2
of
X
². Therefore,
(2.76)
Theorem 2.4.4. For the class of all order types of denumerable sets,
Proof: The previous theorem implies that
(2.77)
It remains to show that
≥
2
. Let γ =
*
ω + ω
. With any sequence of natural
numbers
(2.78)
we form the order type
(2.79)
Then distinct sequences (2.78) always give rise to distinct order types (2.79). In
fact, let
(2.80)
