Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.

Introduction
9
allow us to understand these systems on a theoretical level. Therefore, the first
three approaches can be termed theoretical systems methods, while the others can
be called applied systems techniques. For detailed discussion on various systems
approaches, see (Klir, 1970).
To conclude this chapter, we discuss the foundations of various systems ap-
proaches and some research directions in general systems theory.
1.2.7. Some Research Directions in General Systems Theory
Among the main tasks of general systems theory are (1) define the meaning of
“systems” and related concepts; (2) classify systems and find their properties in the
most general sense; (3) model systems behaviors; (4) study special systems models
logically and methodologically. The first three tasks constitute the theoretical
basics for the concepts of special systems, such as control systems theory, automata,
and information systems theory. That is, the goal of general systems theory is to
establish a higher-level abstract theory without touching on any specific physical
properties. That was why von Bertalanffy believed that general systems theory
deals with formal characteristics of systems structures so that its results can be
applied to research topics in various scientific fields, and that it can be used not
only in physical systems but in any “whole” consisting of interacting “parts”
(von Bertalanffy, 1967, pp. 125–126).
Even though it follows from the previous discussion that systems have a long
history and that many problems discussed in modern systems theory have had
been considered by many great thinkers from different angles in the past several
centuries with different languages, as a theory, especially, as a methodology of
general systems, it is still relative new. In (von Bertalanffy, 1972), von Bertalarnffy
asked how we can define a system. That is, even though the idea of systems has
permeated all of modern science, we still have not obtained an ideal definition for
the concept of systems!
As a matter of fact, as stated in (Department of Business Administration, 1983),
“system” is a generalization of the concept of “structure” in physics but differs
from a structure. A system possesses three important features: (i) order or levels;
(ii) structure of a set; that is, each system consists of at least two subsystems;
(iii) relativity and wholeness; that is, the existence of subsystems is relative and
dependent on each other and conditioning each other.
Tarski (1954–1955) defined the concept of a system with relations as a
nonempty set, called the domain of the system with relations, and a finite se-
quence of relations defined on the domain. Hall and Fagen (1956) discussed the
definition of systems. They believed that a system consisted of a set of objects,
some relations between the objects, and some relations between the attributes of
the objects. In (Systems, 1969–1976), Uyomov proved that the attributes con-
necting the objects of a system can be considered as new objects of the system.
10
Chapter 1
In this way, Hall and Fagen’s definition of systems can be simplified as follows:
A system is a set of objects and some relations between the objects. Mesarovic
(1964) used the language of set theory to define a system as a relation. Therefore,
general systems theory becomes a theory of relations. However, ten years later,
Mesarovic and Takahara (Mesarovic and Takahara, 1975) pointed out that general
systems theory, produced with this definition of systems, does not contain any re-
sults. Does this imply that the definition of systems, given by Mesarovic, contains
something inappropriate? The authors also pointed out that there is no need to
be concerned because the entire research literature of systems theory contains no
results. If that is a fact, does it imply that it is still too early to establish such
a theory? Yi Lin and Yonghao Ma (Lin, 1987; Lin and Ma, 1987) studied the
attempts at defining systems, synthesized all opinions into one with a consider-
ation of future development, and introduced a definition of (general) systems as
follows: S is a (general) system if, and only if, S is an ordered pair (M,R) of
sets, where M is the set of all objects of S and R is a set of relations defined on
M. Here a relation r belongs to R means that there exists an ordinal number n
(nonzero) such that r is a subset of the Cartesian product M
n
. The referee(s) of
(Ma and Lin, 1987) claimed that the definition introduced by Lin and Ma will
produce a good quantity of results, which has been evidenced by results contained
in (Lin, 1987; Lin and Ma, 1987; Ma and Lin, 1987; Lin, 1989d). In this book,
the reader will be led to some of these results. Here, uncertainty, contained in the
concept of “sets,” makes application of systems theory, developed on the definition
of systems by Lin and Ma, contain many uncertain factors. For example, for a
given experimental material, is the totality of molecules constituting the material
a set? Is the collection of all relations between molecules in the material a set?
To deal with these uncertainties, Yi Lin introduced the following epistemological
axiom: The existence of an object is determined by the existence of some particles
of a certain level and of some relations between the particles, which constitute the
object; for details [see (Lin, 1989d)].
We now briefly introduce several research directions in general systems theory.
1.2.7.1. Classical systems theory. Classical systems theory is a mathematical
theory, based on calculus, to study the general principles of structures and structures
with specific properties, and has been used for research and description. Its results
have also been used to solve concrete problems. Because of the generality of
the problems studied, even with special features, parts, and relations between the
parts of a structure, one can still obtain some formal properties of the structure
under concern. For instance, generalized principles of dynamics can be applied to
the totality of molecules or biological objects. That is, these principles can find
applications in chemistry and biology. There are many references here, one of
which is (Wonham, 1979).
1.2.7.2. Catastrophe theory. Catastrophe theory, initiated by Newton and
Leibniz three centuries ago, is a different way of thinking and reasoning about
Introduction
11
“discrete,” “jump” or “discontinuous” changes in a course of events, in an object’s
shape, change in a system’s behavior, and change in ideas themselves. As sug-
gested by its name, this study has been applied to research of literal catastrophes
(e.g., collapse of a bridge, downfall of an empire) and to quiet changes, (e.g.,
dancing of sunlight on the bottom of a pool, transition from wakefulness to sleep).
For more details, see (Poston and Steward, 1978).
1.2.7.3. Compartment theory. In (Rescigno and Segre, 1966), Rescigno and
Segre first studied compartment theory. The basic idea is that the problem or
structure under consideration can be described as a whole consisting of parts
satisfying certain boundary conditions, between which there appear processes of
transportation, such as “chains” or “nipples.” That is, the parts can be chained
together by transportation, or transportation appears between a central part and
its surrounding parts. The mathematical difficulty in dealing with structures with
three or more parts becomes obvious. In this area, Laplace transformation and
networks and graph theory have been successfully used.
1.2.7.4.
Cybernetics. Cybernetics is a theory on systems and their environ-
ments, internal information transportation of systems, and impacts on the environ-
ment of controlled systems. This theory has found many applications. Because
of its usefulness, many scholars do not see it as a part of systems theory. Cy-
bernetics has often been used to describe the formal structure of some “action
processes.” Even though the structure of the system under concern is not clearly
given, and the system is an input—output “black” box, cybernetics can still offer
some understanding about that structure. Therefore, cybernetics has been applied
in many areas, including hydraulics, electricity, ecology, markets, etc. For more
information, see (Bayliss, 1966; Milsum, 1966).
1.2.7.5.
Fuzzy mathematics. Fuzzy mathematics is a theory dealing with the
rapprochement between the precision of classical mathematics and the pervasive
imprecision of the real world. The fundamental concept here is fuzzy sets, which
are classes with boundaries that are not sharp in which the transition from mem-
bership to nonmembership is gradual rather than abrupt. At present, we are unable
to design machines that can compete with humans in the performance of tasks such
as recognition of speech, translation of languages, comprehension of meanings,
abstraction and generalization, decision making with uncertainty, and, above all,
summarization of information. This stems from a fundamental difference between
human intelligence, containing fuzziness, and machine intelligence, based on pre-
cision. Consisting of a body of new concepts and techniques, this theory accepts
fuzziness as an all-pervasive reality of human existence, which has opened many
new frontiers in psychology, sociology, political science, philosophy, physiology,
economics, linguistics, operations research, management science, and other fields.
The literature in this research area is plentiful, and I will not list any here.
12
Chapter 1
1.2.7.6. Game theory.
According to Quastler, game theory is a systems theory,
since it deals with the behaviors of (
n
) ideal players with the ability to reason and
make decisions, whose goal is to win more than to lose. One goal of this research
is how to apply optimal strategies to confront other players (or the environment).
That is, game theory is about the study of systems with special reaction forces. A
good reference is (Shubik, 1983).
1.2.7.7. Genetic algorithms. Genetic algorithms (GAs) have been applied
in many areas, including economics, political science, psychology, linguistics,
biology, computer science, etc. GAS are search procedures based on the mechanics
of natural selection and natural genetics. They combine survival of the fittest
among string structures with a structured yet randomized information exchange
to form a search algorithm with some of the innovative flair of human search.
The goals of this research are twofold: (1) to abstract and rigorously explain the
adaptive processes of natural systems, and (2) to design artificial systems software
that retains the important mechanisms of natural systems. This approach has led
to important discoveries in both natural and artificial science. The central theme
of research here has been robustness, the balance between efficiency and efficacy
necessary for survival in many different environments. A good introductory book
on this subject matter is (Goldberg, 1989), and the classic is (Holland, 1975).
1.2.7.8. Graph theory. Besides the quantitative study of structures, many
problems deal with the organization and topological structures of the systems
of interest. There exist many methods useful to this research. Graph analysis,
especially directed graph theory, describes in detail the construction of relations
between systems. This method has been successfully applied in many different
areas, including biology [see, for example, (Rashevsky, 1956)]. Combined with
matrix theory in mathematics, the characteristics of the models, developed in graph
theory are similar to those of compartment theory, so it establishes relations with
the theory of open systems.
1.2.7.9. Information theory. Based on the opinion of Shannon and Weaver
(1949), information theory is established on the concept of information, which is
defined by an expression similar to one with negative entropy in thermodynamics.
Quastler (1955) believes that information can be considered as a measure of the
structure of organization. Although information theory is very important in the
engineering of communication, research results in other areas of application have
not yielded any convincing consequences.
1.2.7.10. Navier–Stokes equation and chaos. Even though the Navier–Stokes
equation has been successfully applied in weather forecasting (short term only), its
study has recently given some new understanding, which has led to the new science
called Chaos. On one hand, the concept of chaos, which has several different
meanings, has created a burst of research in almost all areas of science. People
are trying to find and understand chaos. On the other hand, some scholars have
Introduction
13
shown that the original chaos, introduced by Lorenz in the study of simplifying
Navier–Stokes equation, has nothing to do with modem chaos. In fact, it is either
an illusion of a concept of a higher dimensional space or a misunderstanding in
computer-aided calculation. Here I list only two references (Cohen and Steward,
1994; Gleick, 1987).
1.2.7.11. Networks. Network theory can be considered as part of set theory,
or graph theory, or compartment theory. The main structure dealt with is net
structures of systems. It has been applied to neural networks; for details, see
(Rapoport, 1949).
1.2.7.12. Set theory. All the general definitions and properties of structures
have been given in terms of set theory. For example, open and closed systems
can be described by axioms using the language of set theory. All research along
this line was originated by Mesarovic (1964, pp. 1–24). Most of this research,
carried out since 1964, is related to the concept of systems and related topics, not to
solving practical problems, at least until recently [see (Lin and Ma, 1987; Ma and
Lin, 1987; Lin, 1989d; Lin and Qiu, 1987)]. Because of the use of the language
of set theory, the language and methodology of category theory can be employed
to classify structures. On the other hand, algebraic methods can be introduced so
that concepts, such as linear and nonlinear structures, have been introduced. For
related references, see (Mesarovic and Takahara, 1975).
1.2.7.13. Simulation. If the structures, described by differential equations,
contain nonlinear equations, in general, there is no way to solve the systems.
Because of this reason, computer simulation becomes an important method. This
method not only saves time and human labor, but also opens up research areas in
which, mathematically, we do not know if the solution exists. This kind of system
cannot be solved by known mathematics. On the other hand, specific experiments
in laboratories can be replaced by computer simulations. For example, computer-
aided design uses computer simulation as a substitute for laboratory experiments.
At the same time, the mathematical structure or model obtained by computer
simulation can be evaluated by experimental data. For example, Hess (1969)
employed this method to compute a 14-th step chemical reaction in human cells,
which was described by a system of more than 100 nonlinear differential equations.
As a matter of fact, this method has often been used in the study of markets and
populations.
1.2.7.14. Statistics. Einstein said (1922, p. 60):
The belief in an external world independent of the perceiving subject is the basis
of all natural science. Since, however, sense perception only gives information of
this external world or of “physical reality” indirectly, we can only grasp the latter
by speculative means. It follows from this that our notion of physical reality can
never be final.
Chapter 1
14
Based on this understanding, statistics is a mathematical theory of how to
predict and comprehend “reality” according to a small sample, collected with
reference to some prior mathematical analysis. This theory is not of what event
causes another event (i.e., causality) but about what event will imply that another
will occur. Successful applications of statistics can be found in almost all applied
areas of human endeavors. One of the best references here is Box, Hunter, and
Hunter’s classic (Box et al., 1978).
1.2.7.1.5. Theory of automata. The theory of automata concerns an ideal
automaton with input and output, and its ability to be corrected and learn
(Minsky, 1967). One such example is the Turing machine (Turing, 1936). In
ordinary language, the Turing machine is an ideal machine which can print “1”
and “0” on an infinitely long tape. It can be shown that, no matter how compli-
cated a process can be, if it can be expressed by finite steps of logic rules and
calculations, then this process can be simulated by a machine. From this fact, the
future of this theory can be seen.
1.3. A Few Thoughts
It can be seen that systems theory is very young. Researchers are trying to
find more practical examples and general properties, and are testing and rethinking
the theory. That is why new ideas have been appearing quickly, and consequent
discussions have been intensive. It can be foreseen that the development of
modern science and technology will be the effective motivation and method to
test the duration and significance of ideas and thoughts in general systems theory.
Based on the thoughts of general systems theory, some scientific workers have
simplified the question in which administrators of scientific research are interested
to the following: Can science be studied as a system? This is an important and
practical problem since if this question can be studied deeply with reasonable
outcome, the human exploration of nature might be able to go to a higher level
(Yablonsky, 1984).
CHAPTER 2
Naive Set Theory
Set theory, created by Georg Cantor (1845–1918), is one of the greatest creations
of the human mind. Everyone who studies it is fascinated by it. More important,
however, is that the theory has become of the greatest importance for the entire
spectrum of mathematics. It has given rise to new branches of mathematics, or at
least first rendered the possibility for their further development, such as the theory
of point sets, theory of real functions, and topology. Finally, the theory of sets
has had influence on the investigation of the foundation of mathematics, as well as
through the generality of its concepts, as a connecting link between mathematics
and philosophy.
We will present the basic features of Cantor’s naive set theory. The basic
concepts and methods of proofs will be used in the development of general systems
theory.
2.1.
A Set and Its Classification
According to Cantor a set M is “a collection into a whole, of finite, well-
distinguished objects (called the ‘elements’ of M) of our perception or of our
thoughts.” For example, the 38 students in a classroom constitute a set of 38
elements; the totality of even numbers, a set of infinitely many elements; the
vertices of a die, a set of 8 elements; the points on a circle, a set of infinitely many
elements.
Two sets M and N are equal, in symbols M = N, if they contain the same
elements. For example, if M = {1,2,3} and N = {2,1,3}, then M = N. (Sets,
in general, are designated by enclosing their elements in braces or by a symbol
like {
x :
Φ
(
x
)}, which means that the set consists of all the elements satisfying the
proposition
Φ
.)
The notation M ≠ N means that the sets M and N are different. Further, m ∈ M
means that m is an element of the set M, whereas m
∉ M denotes that m is not
an element in M. M
⊆ N denotes inclusion; that is, M is a subset of N, or all
elements of M also belong to N.
15
16
ƒ(
x) ≠ ƒ(y
)
0, 1, 2, 3, . . .
–1, –2, –3, . . .
(2.2)
(2.3)
Chapter 2
Proposition 2.1.1. M = N iff M ⊆ ⊆ N and N ⊆ ⊆ M.
A mapping (or a function) from a set M into a set N is a rule under which each
element in M is assigned to an element in N. Generally, lower case letters, say,
ƒ, g, and h, will be used to indicate mappings. Let ƒ be a mapping from the set
M into the set N, denoted by ƒ : M
→ N. Then for each element m ∈ M, ƒ(m
)
indicates the element in N which is assigned to the element m.
The mapping ƒ : M → N is onto (or surjective), if for each element n ∈ N,
there exists an element m
∈ M such that ƒ(
m
) = n. The mapping ƒ : M → N is
1–1 (or one-to-one, or injective) if for arbitrary distinct elements x and y
∈ M,
(2.1)
The mapping ƒ :
M
→
N
is a bijection (or a bijective mapping) if ƒ is both surjective
and injective.
Sets M and N are equipollent if there exists a bijection of M onto N . The
equipollence relation between sets classifies the collection of all sets into classes
such that each class contains all the equipollent sets. Another coarse classification
of sets distinguishes the collection of all sets into finite, denumerable and uncount-
able sets according to whether the sets contain a finite number of elements, or are
equipollent to the set of all natural numbers N, or do not satisfy the previous two
conditions; i.e., they contain infinitely many elements and are not equipollent to
N
.
Proposition 2.1.2. A set X is denumerable iff it can be written as a sequence
{
x
0
, x
1
, x
2
, x
3
, ...}.
This fact implies that an infinite set X is denumerable iff to every element x of
the set, precisely one natural number corresponds to it and
vice versa
.
Theorem 2.1.1. The set of all integers is denumerable.
Proof: Let us write the integers as follows:
Then the set of all integers can be written as the sequence
{0, 1 –1, 2, –2, 3, –3, ..., n, –
n
, ...}
Theorem 2.1.2. The set of all rational numbers is denumerable.

Naive Set Theory
17
r
Proof: Let us first deal with the set of all positive rational numbers. We can
write all whole numbers in order of magnitude (i.e., all numbers with denominator
1), then all fractions with denominator 2, then all fractions with denominator 3,
etc. Thus, we have the rows of numbers
(2.4)
If we write the numbers in the order indicated by the arrows (leaving out numbers
which have already appeared), then every positive rational number certainly ap-
pears, and only once. The collection of these rational numbers is thus written as a
sequence
(2.5)
If we denote this sequence by {
r
1
,r
2
,r
3
, ... }, then obviously
{0,
r
1
,–r
1
,
r
2
,–
r
2
,
3
,–
r
3
,...}
is the set of all rational numbers, and the denumerability of this set is established.
The following theorem shows that not every set of real numbers is denumerable.
Theorem 2.1.3. The set of all points in the closed interval [0, 1] is uncountable.
Proof: We prove the theorem by a diagonal method, called the second, or
Cantor, diagonal method. Suppose that the closed interval [0, 1] is denumerable;
then the open internal (0, 1) is also denumerable. From Proposition 2.1.2 it follows
that the points in (0, 1) can be written as the sequence
b
0
,b1
,b
2
,b
3
,...
(2.6)
We now write each of them as infinite decimal numbers by putting in enough zeros
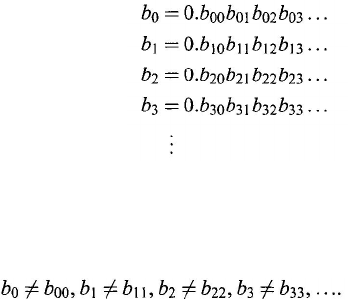
18
Chapter 2
whenever necessary. Then
(2.7)
Now we construct a number b ∈ (0, 1), defined by
b = 0.
b
0
b
1
b
2
b
3
...
(2.8)
such that Then b is not contained in the
sequence {
b
0
,b
1
,b
2
,...}
, contradiction. This contradiction implies that the set of
all points in the interval (0, 1) is uncountable.
The sets X and Y are of the same cardinality if they are equipollent. Generally,
to every set X the cardinality of X is assigned and is denoted by
⏐X
⏐.
The equality
⏐
X
⏐
=
⏐
Y
⏐ holds iff X and Y are equipollent. For a finite set X the cardinality
of X is equal to the number of elements of X. The cardinality assigned to each
denumerable set is denoted by
ℵ
0
(read aleph zero), and the cardinality assigned
to the set of all real numbers is denoted by c (called the continuum).
Let
m
and
n
be two cardinalities, and let
⏐
X
⏐
=
m
and
⏐
Y⏐ = n. We say that m
is not larger than n, or that n is not smaller than m, and we write m
≤ n or n ≥ m,
if there exists a one-to-one mapping of X into Y. We say that m is smaller than n,
or that n is larger than m, and we write m < n or n > m, if m
≤ n and X and Y are
not equipollent.
Corollary 2.1.1.
ℵ
0
< c.
The following fact says that for any fixed cardinality
m
there exists a set whose
cardinality is larger than m.
Theorem 2.1.4. Let X be a set and 2
X
the set of all subsets of X, which is called
the power set of X. Then
⏐
X
⏐
<
⏐2
X
⏐
(2.9)
Proof: Define a mapping ƒ: X → 2
X
by letting ƒ(x) = {x} for each x ∈ X.
Then ƒ is one-to-one, so
⏐X
⏐ ≤ ⏐
2
X
⏐
. We must now show that X and 2
X
are
not equipollent. We prove this by contradiction. Suppose that X and 2
X
are
