Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.


Naive Set Theory
19
equipollent. There then exists a bijection h from X onto 2
X
. Define a subset of X
as follows:
Since h is onto, it follows that there exists an element y
∈ X such that
(2.10)
h
(
y) = A
(2.11)
There now exist two possibilities: (1) y
∈ A or (2) y ∉ A. If case (1) holds, then
y
∈ A = h
(
y
). This implies that y ∉ A, contradiction. If case (2) is true, then
y
∉ h(
y
) = A. So y ∈ A, another contradiction. Therefore, the bijection h cannot
exist, and
⏐
X
⏐
<
⏐
2
X
⏐
.
2.2. Operations of Sets
Let X be a set. A set Y is called a proper subset of X, denoted Y ⊂ X, if Y
is a subset of X and X
≠ Y. A set Z of those elements of X which do not belong
at the same time to the subset Y is called the complement of Y with respect to X;
in symbols, Z = X – Y. When Y is not a proper subset of X, Z may not contain
any element. In this case, we introduce an ideal set, called the empty set, Ø. The
empty set is classed with the finite sets. It is a subset of every set and, in particular,
of itself.
Theorem 2.2.1. Every subset of a denumerable set is at most denumerable.
Proof: Let X = {x
0
,x
1
,x
2
, ... } be a denumerable set and Y ⊂ X. Then in X
there exists a first element x
k
. This is followed
1
which belongs to Y ; let y
1
= x
k
1
again by a first element, denoted by
x
k
2
, in
X,
which belongs to
Y
; let
y
2
= x
k
2
, etc.
The process does or does not terminate, according to whether Y is finite. Since X
contains all the elements of Y, the possibly terminating sequence {
1
,
k
k
2
, k
3
, ... }
comprises precisely the elements of Y. Therefore, Y is finite or denumerable.
The union of finitely or infinitely many sets is defined to be the set of those
elements which belong to at least one of the sets. The union U of an at most
denumerable number of sets X
0
,
X
1
,
X
2
, ... is written in the form
(2.12)
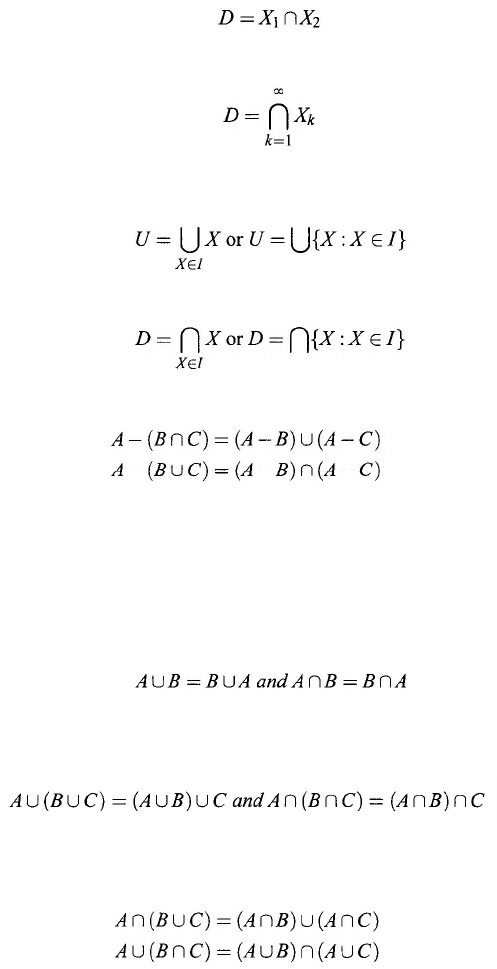
20
Chapter 2
The intersection of arbitrarily many sets is defined to be the set of those
elements which belong to each of the aforesaid sets. For the intersection D of two
sets
X
1
and X
2
, we write
and
(2.13)
and for the intersection of at most denumerably many sets,
(2.14)
Let I be a collection of sets. The union U and the intersection D of the sets in I is
written
(2.15)
(2.16)
Theorem 2.2.2 [De Morgan’s Laws]. Suppose that A, B, and C are sets. Then
(2.17)
(2.18)
Proof: We prove only the first equality. For any element x, x
∈ A – (B
∩
C
)
iff x
∈ A and x ∉ B
∩
C, iff x ∈ A and either x ∉ B or x ∉ C, iff either x ∈ A and
x
∉ B or x ∈ A and x ∉ C, iff x ∈ ( A – B
)
∪
(
A – C).
Proposition 2.2.1 [Commutative Laws]. Let A and B be two sets. Then
(2.19)
The proof follows immediately from the definitions of union and intersection.
Proposition 2.2.2 [Associative Laws]. Let A, B, and C be sets. Then
(2.20)
The proof follows immediately from the definitions of union and intersection.
Proposition 2.2.3 [Distributive Laws]. Let A, B, and C be sets. Then,
(2.21)
(2.22)

Naive Set Theory 21
The proof is left to the reader.
Proposition 2.2.4 [Laws of Tautology]. For any set A,
The proof is straightforward and is omitted.
The following identities are given without proof.
Proposition 2.2.5. Let A, B and C be sets. Then
The following formulas illustrate the analogy between the inclusion relation
and the “less than or equal to” relation in arithmetic:
(2.23)
Proposition 2.2.6. For arbitrary sets A, B, C, and D, the following are true:
where
→ means “imply.”
For the union and intersection of a collection I of sets, we have the following
results.
Proposition 2.2.7 [De Morgan’s Laws]. Let A be an arbitrary set. Then
Proof:
(1) For any element x,
iff
x
∈
A
and iff
x
∈
A
and
there exists an X ∈ I such that x ∉ X, iff there exists X ∈ I such that
iff
22
Chapter 2
(2)
For any element
x
, x ∈ A –
∪
X
∈
I
X iff x ∈ A and for each set X ∈ I, x ∉ X
,
iff for each set X ∈ I, x ∈ A–X, iff x ∈
(
A–X).
Let
x
and
y
be two elements. The ordered pair (
x,y) is the set {{x
}, {
x,y
}}. We
call x the first term (or coordinate) of (x,y) and y the second term (or coordinate)
of (
x,y
).
Theorem 2.2.3. In order that ( a,b) = (
c,d
), it is necessary and sufficient that
a = c and b = d.
Proof: The sufficiency part is clear. To prove necessity, suppose that (
a,b
) =
(
c,d). From the definition of ordered pairs, it follows that {
c
} ∈ (
a,b
) and
{
c,d} ∈ (
a,b
); that is, (i) {
c
} = {
a
} or (ii) {
c
} = {
a,b
}, and (iii) {
c,d
} = {
a
} or
(iv) {c,d} = {a,b
}.
Equality (ii) holds if a = b = c. Equalities (iii) and (iv) are then equivalent
and it follows that c = d = a. Hence, we obtain a = c = b = d , in which case the
theorem holds. Similarly, one can check that the theorem holds for case (iii). It
remains to show that the theorem holds for cases (i) and (iv). We then have c = a
and either c = b or d = b . If c = b, then (ii) holds and this case has already been
considered. If d = b, then a = c and b = d, which proves the theorem.
The Cartesian product of two sets
X
and
Y
is defined to be the set of all ordered
pairs (
x,y) such that x ∈ X and y ∈ Y. This product is denoted by X × Y . If X =
or Y = , then obviously X × Y = . Certain properties of Cartesian products are
similar to the properties of multiplication of numbers. For example, we have the
following results:
Proposition 2.2.8 [Distributive Laws]. Let X
1
, X
2
, and Y be sets. Then
(1)
(
X
1
∪
X
2
) × Y = (X
1
× Y
)
∪
(
X
2
×
Y
),
(2)
Y
× (
X
1
∪
X
2
) = (Y × X
1
)
∪
(Y × X
2
),
(3)
(
X
1
∩
X
2
) × Y = (X
1
× Y
)
∩
(
X
2
× Y
),
(4) Y × (
X
1
∩
X
2
) = (Y × X
1
)
∩
(
Y × X
2
),
(5)
(
X
1
– X
2
) × Y = (
X
1
×
Y
) – (
X
2
×
Y
),
(6) Y × (X
1
–X
2
) = (Y × X
1
) – (
Y × X
2
).
Proof: We prove only the first equation. For an ordered pair (x,y), (x,y) ∈
(X
1
∪
X
2
) × Y iff x ∈ X
1
∪
X
2
and y ∈ Y, iff either x ∈ X
1
or x ∈ X
2
and y ∈ Y,
Naive Set Theory 23
iff either x ∈ X
1
and y ∈ Y or x ∈ X
2
and y ∈ Y, iff either (x,y) ∈ X
1
× Y or
(
x,y
)
∈
X
2
× Y, iff (x,y
)
∈
(
X
1
× Y)
∪
(X
2
×
Y
).
A subset f ⊂ X × Y is called a function or mapping from X into Y if for any
x
∈ X and any y
1
and y
2
∈ Y, (x,y
1
), (
x,y
2
) ∈ f implies that y
1
= y
2
= y. In this
case, the element y is denoted f
(
x). The function f is written f : X → Y. When
each x
∈ X belongs to a pair in f , the function f is defined on X. Otherwise, f is
called a partial function from X to Y.
Theorem 2.2.4. If f : X
→ Y is a function, then f
–1
= {(x,y) : (
y,x
) ∈ f } is a
partial function from Y into X iff f is one-to-one; that is, if (
x
1
,y
) and (
x
2
,y
) ∈ f
then x
1
= x
2
.
Proof: By definition, the subset ƒ
–1
is a partial function from Y into X iff
for any y, x
1
and x
2
, (y,x
1
) and (y,x
2
) ∈ f
–1
implies that x
1
= x
2
. That is, if
f (
x
1
) = y = f (x
2
), then x
1
= x
2
. Thus, f is one-to-one.
2.3. Arithmetic of Cardinal Numbers
Let X and Y be two sets. The notation X ~ Y indicates that the sets are
equipollent. The following result says that the equipollence relation is reflexive,
symmetric, and transitive.
Theorem 2.3.1. For arbitrary sets A, B, and C the following holds:
(1)
Reflexive property: A ~ A.
(2)
Symmetric property: A ~ B implies B ~ A.
(3)
Transitive property: (A ~ B) and (B ~ C) imply A ~ C.
The proof is straightforward and is omitted.
Example 2.3.1. Since the concept of equipollence is of fundamental importance,
we illustrate it by some examples.
(a) The sets of the points of the intervals [0, 1], [0, 1), (0, 1], and (0, 1) are
equipollent to each other.
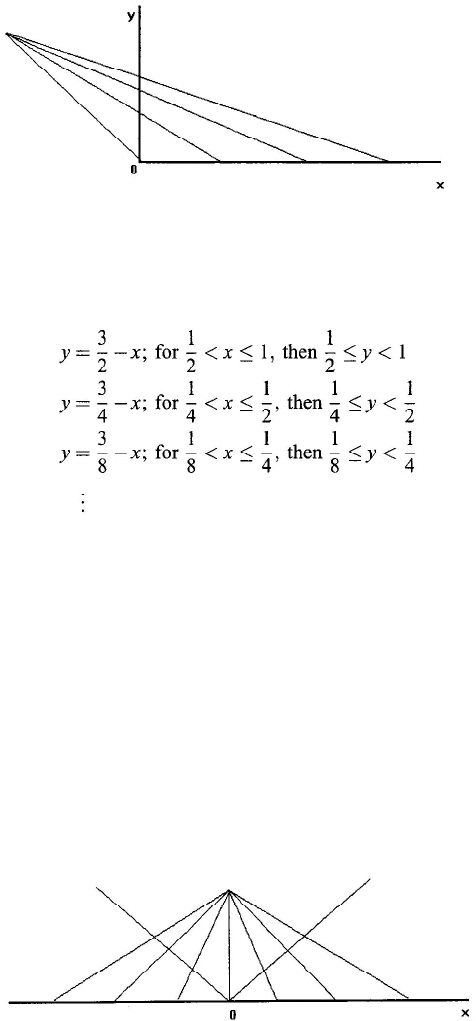
24
Chapter 2
Figure 2.1. A half-line obtained by central projection.
First, let us prove that (0, 1] ~ (0, 1). We denote the points of the first interval
by x and those of the second by y
, and set up the following correspondence:
It is evident that we have already set up a 1–1 correspondence between the two
intervals. This proves our assertion.
We can show analogously that [0, 1) ~ (0, 1). From this it follows finally that
[0, 1) ~ [0, 1].
(b) A half-line and an entire line are equipollent to an interval.
A half-line can be obtained by central projection from an interval erected at
right angles to it and open above (Fig. 2.1). A full line can be obtained similarly
from a bent, open interval (Fig. 2.2).
(c) Two finite sets are equipollent if, and only if, they contain equally many
elements.
(d) An infinite set can be equipollent to one of its proper subsets. This is
shown by the equipollence of the sets {1,2,3, . . . } and {2, 4, 6, . . . }. Infinite sets
Figure 2.2. A full line obtained from a bent open interval.
Naive Set Theory
25
thus exhibit in this respect an entirely different behavior from that of finite sets
[see example (c)]. This property can therefore be used to distinguish finite and
infinite sets independently of any enumeration.
(e) The set of all real functions defined on the interval [0, 1] is neither denu-
merable nor equipollent to the continuum.
The proof of this fact is obtained by a procedure which is again essentially
the second diagonal method. It is clear not only that there are infinitely many
distinct functions on [0, 1] but also that there exist uncountably many. For, at the
point x = 0 alone, the functions can already assume the uncountably many values
between 0 and 1. Thus, there remains to be proved only that the set of functions
is not equipollent to the continuum.
Suppose that the set of functions were equipollent to the continuum. Then it
would be possible to make the function f
(
x) and the points z of [0, 1] correspond
in a 1–1 manner. Denote by f
z
(
x) the function thus assigned to the point z. Now,
construct a function g(z) defined on the interval 0
≤ z ≤ 1 with the property that,
at every point z, g
(
z) ≠ f
z
(
z). Since g
(
z) is also a function defined on [0, 1], it
must coincide with an f
u
(
x); hence, in particular, g
(
u
) = f
u
(
u
). This, however, is
excluded by the definition of g(z). The assumption that the set of our functions is
equipollent to the continuum has thus led to a contradiction.
When two sets X and Y are given, precisely one of the following cases can
occur:
(a)
X is equipollent to a subset of Y.
(b)
X is equipollent to no subsets of Y.
Likewise, exactly one of the following possibilities can take place:
(1)
Y is equipollent to a subset of X,
(2)
Y is equipollent to no subsets of X.
There are four combinations of these two pairs of cases, vis., (a)(1), (a)(2),
(b)(1), (b)(2). In the two middle cases
⏐
X
⏐< ⏐
Y
⏐
and
⏐
Y
⏐ <⏐
X
⏐.
Case (b)(2) means
that X and Y are not comparable. We will show that this case never occurs. Case
(a)(1) is discussed next.
Theorem 2.3.2 [Bernstein’s Equipollence Theorem].
If each of two sets X and
Y is equipollent to a subset of the other, then X ~ Y.
Proof: Assume that f : X
→ Y and g : Y → X are both 1–1 functions. Let
A
0
= X – g
(
Y ), B
0
= Y – f
(
X
), and define inductively
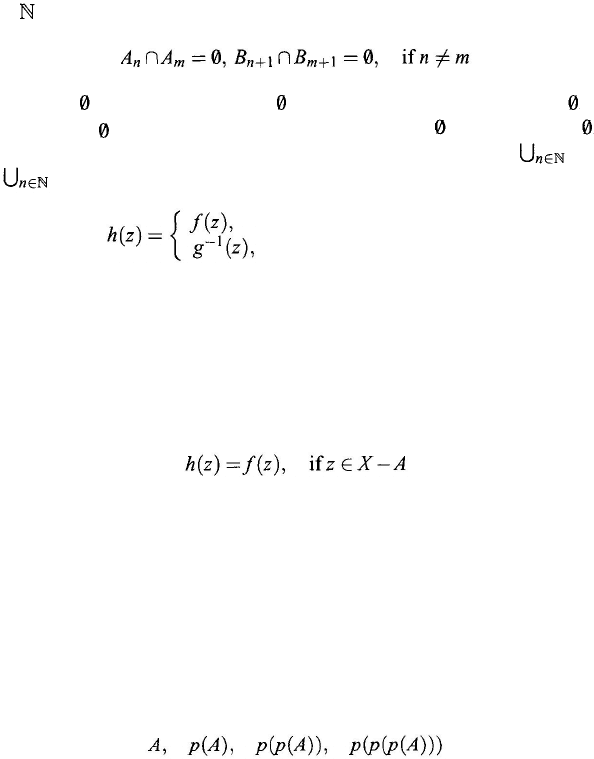
26 Chapter 2
where
= {0,1,2,. . . }. Then by induction on n we have
(2.24)
If
A
n
∩
A
m
=
, then
B
n+1
∩
B
m
+1
=
since ƒ is 1–1 and if B
n
∩
B
m
= , then
A
n +1
∩
A
m+1
=
since g is 1–1. So, since A
0
∩
A
n
=
and B
0
∩
B
n
=
, by
induction, for each n ≠ 0, Eq. (2.24) follows. Now, define A =
A
n
and
B = B
n
and define a 1–1 function h from A onto B by
if
z
∈
A
m
and m is even
if z
∈ A
m
and m is odd
(2.25)
Then if t
∈ B
m
and
m
is even,
h
–1
(
t
) = g
(
t
), and if
m
is odd then
h
–1
(
t
) = ƒ
–1
(t).
So, h is from A onto B.
In addition, ƒ is 1–1 onto between X – A and Y – B since if z
∈ X – A, then
ƒ(z
)
∉
B
(since ƒ (
z
)
∈
B
m
implies that
m
≠
0 and
z
∈
A
m
–1
); similarly, if
t
∈
Y
–
B,
then t = ƒ(z) for some z ∈ X (otherwise t ∈ B
0
), and z ∈ A implies t ∈ B. Now,
we extend h as follows:
(2.26)
Then h is 1–1 from X onto Y, which establishes the equipollence between X and
Y.
We know from Section 2.1 that to each set
X
a cardinality (or cardinal number)
is assigned. Corollary 2.1.1 says that besides the finite cardinal numbers, the
number
ℵ
0
, and the continuum
c,
there exist infinitely many other cardinal numbers.
In the sequel, we use p
(
X) to indicate the power set of the set X.
Theorem 2.3.3. Let A be an arbitrary set. Then no two of the sets
(2.27)
are equipollent.
Proof: Let p
κ
be the κth set in the sequence (2.27) and suppose that there
exist
κ and ι such that κ > ι and p
κ
is equipollent to a subset of p
ι
. The set
p
κ
–1
is clearly equipollent to a subset of p
κ
,
namely to the subset of singletons {x
},
where x ∈ p
κ
–1
. Thus, the set p
κ –1
is equipollent to a subset of
p
ι
. Repeating this
argument, we conclude that each of the sets p
κ
,p
κ
–1
, . . . ,
p
ι +1
is equipollent to
some subset of p
ι
, but this contradicts Corollary 2.1.1 and Theorem 2.3.2 because
p
ι+1
=
p
(p
ι
).

Naive Set Theory
27
Theorem 2.3.4. Let the family A have the property that for every X ∈ A there
exists a set Y
∈ A which is not equipollent to any subset of X. Then the union
∪
X
∈
A
X is not equipollent to any X
∈
A nor to any subset of X
∈
A.
Proof: Assume that there exists an X ∈ A such that It
follows that there exists a 1–1 function ƒ such that By assumption
of the theorem there is a set
Y
∈
A
which is not equipollent to any subset of
X.
Since
we have that is, ƒ(Y) ⊂ X
1
and consequently
Y ~ ƒ(Y)
⊂ X. The contradiction thus shows that
Theorems 2.3.3 and 2.3.4 give us some ideas about how many distinct infinite
cardinal numbers exist. Starting with the set of nonnegative integers which has
power
ℵ
0
, we can construct the sets
(2.28)
no two of which are equipollent by Theorem 2.3.3. In this way we obtain infinitely
many distinct cardinal numbers. Theorem 2.3.4 says the union
where for each n
∈ , has a cardinal number
different from each of the sets in sequence (2.28) and from each of their subsets.
Again applying Theorem 2.3.3 we obtain the sequence of sets
S, p
(
S), p
(
p
(
S)), p
(
p
(
p
(
S
))), ...
(2.29)
no two of which are equipollent and none of which is equipollent to any of the
sets in sequence (2.28). We obtain in this way a new infinite number of distinct
cardinalities.
We may still obtain other cardinal numbers by constructing the family B =
(
S) and a new sequence
B, p
(
B), p
(
p
(
B)), p
(
p
(
p
(
B
))), ...
(2.30)
This procedure continues infinitely. We see that the hierarchy of distinct infinite
cardinal numbers is comparably richer than the hierarchy of finite cardinalities,
which coincides with
We now begin to define the operations of addition, multiplication, and expo-
nentiation for cardinal numbers. Let m and n be cardinal numbers and X and Y
two disjoint sets such that
⏐
X
⏐
=
m
and
⏐
Y
⏐
=
n.
Then define
m
+
n
=
⏐
X
∪
Y
⏐
(2.31)
For the definition to have a meaning, it is necessary to show that the sum
m + n
does not depend on the choice of the sets X and Y. Therefore, let X* and Y* be
two disjoint sets with
⏐X*⏐ = ⏐ X⏐ and |Y*| = |Y|. Then it is not hard to see that
X
*
∪
Y
*
~
X
∪
Y
.

28
Chapter 2
Theorem 2.3.5. The addition of cardinal numbers is commutative and associa-
tive; that is, for arbitrary cardinal numbers n
1
, n
2
, and n
3
,
(2.32)
(2.33)
The proof follows from the definition of addition of cardinal numbers.
Theorem 2.3.6. Let m
i
and n
i
be cardinal numbers, i = 1, 2, such that
m
i
≤
n
i
.
Then
Proof:
Let
X
i
and Y
i
,
i
= 1, 2, be four pairwise disjoint sets such that
and . Then by hypothesis there exist 1–1 functions
Define a new function g :
by
(2.35)
(2.34)
We then check that
g
is a one-to-one function from
X
∪
X
into
1
2
Y
1
∪
Y
2
. This gives
m
1
+
m
2
≤
n
1
+ n
2
.
We cannot, however, always infer from
m
1
<
n
1
and
m
2
≤
n
2
that
m
1
+
m
2
<
n
but
1
+ n
n
<
ℵ
0
and
ℵ
0
≤
ℵ
0
n
+
ℵ
0
2
. For example, for every
n
∈
we have
=
ℵ
0
=
ℵ
0
+
ℵ
0
.
The cardinal number
m
is the product of
n
1
and
n
2
,
denoted
m = n
1
⋅ n
2
, if every
set of power
m
is equipollent to the Cartesian product
A
1
× A
2
, where
i = 1,2. Thus,
Theorem 2.3.7.
The multiplication of cardinal numbers is commutative, associa-
tive, and distributive over addition:
(2.36)
(2.37)
(2.38)
Proof: Equation (2.36) is an immediate consequence of the relation
A × B ~ B × A
Equation (2.37) follows from
[
A ×(
B × C
)] ~ [(
A × B
)
× C
]
