Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.


70
Chapter 3
We use natural numbers to count finite sets. The Axiom of Choice tells that
every set can be counted by an ordinal. Therefore, we use natural numbers to
indicate finite ordinals.
Let
α be an arbitrary ordinal. The successor S(α) of the ordinal is defined by
S (
α)=α ∪
{
α}. Then S
(
α) is also an ordinal, and we have
0 = Ø
1 = S(
Ø)
2 = S
(
2
)
3=S
(
2),
...
(3.17)
Intuitively, natural numbers are those ordinals obtained by applying
S
to Ø a finite
number of times.
An ordinal
α is a successor ordinal (or isolated ordinal) if ∃ β( α = S(β)). It is
a limit ordinal if
α ≠ 0 and α is not a successor ordinal. For example, let ω be the
set of all natural numbers and 0. Then
ω is an ordinal and all smaller ordinals are
successor ordinals or 0. So
ω is a limit ordinal, since if not it would be a natural
number, and hence
ω is the least limit ordinal. Actually, the Axiom of Infinity is
equivalent to postulating the existence of a limit ordinal.
The following theorem shows that the elements of
ω are the real natural
numbers.
Theorem 3.2.5. The Peano postulates are
(1)
0
∈
ω
.
(2)
(3)
(4)
(Induction)
Proof: For (4), if X
≠ ω, let γ be the least element of ω
\
X, and show that γ
is a limit ordinal < ω, contradiction.
Let α and β be two ordinals.
Define
α + β
=
type (
α
×
{0}
∪
β
×
{1},
H
),
where
Theorem 3.2.6. For any
α, β, γ:
(1)
(2)
(3)
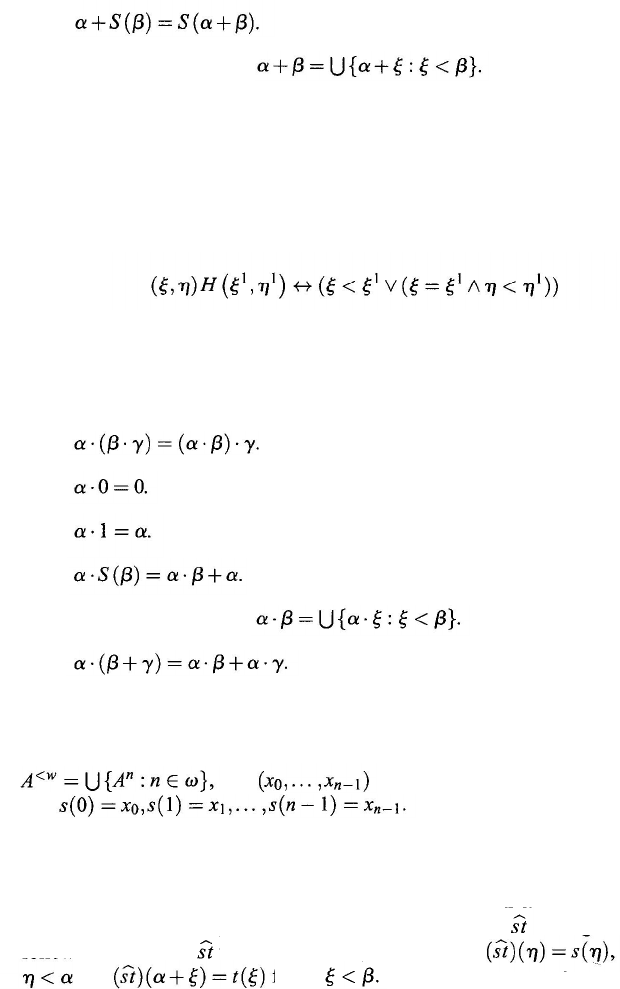
Axiomatic Set Theory
71
(4)
(5) If
β
is a limit ordinal,
Proof: The results are straightforward from the definition of addition.
Recall that the addition of ordinals is not commutative. Let α and β be two
ordinals. We define the multiplication
α · β = type (β × α, H ), where H is the
lexicographic order on
β
×
α:
(3.18)
Again, we get directly from the definition the basic properties of the multiplication
of ordinals.
Theorem 3.2.7. For any
α, β, γ::
(1)
(2)
(3)
(4)
(5) If
β is a limit ordinal,
(6)
We, again, need to remember that the multiplication of ordinals is not commu-
tative and the distributive law (6) fails for multiplication on the right.
Let A be a set. We define A
n
to be the set of all functions from n to A,
and is the function s with domain n such
that
Under these definitions, A² and
A × A
are not the same, but there is an obvious 1–1 correspondence between them.
In general, if s is a function with domain(s) = I, we may think of I as an index
set and s as a sequence indexed by I. In this case, we write s
i
for s
(
i
). When D
(
s
)
is an ordinal α, we may think of s as a sequence of length α. If D
(
t
) = β, we
may concatenate the sequences s and t to form a sequence of length
α + β as
follows: the function with domain
α + β is defined by for each
and
for all
We have seen that there need not exist a set of the form {
x : φ (x
) }. But there is
nothing wrong with thinking about such collections, and they sometimes provide
useful motivation. Informally, we call any collection of the form {x :
φ
(
x)} a
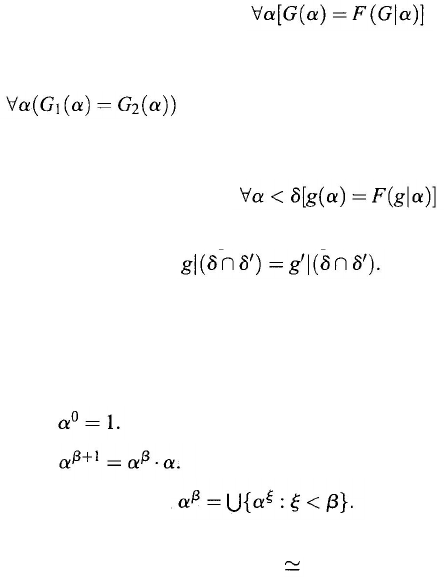
72
Chapter 3
class. A proper class is a class which is not a set (because it is too “big”). We use
V and ON to indicate the following two classes
V = {x : x = x
}
(3.19)
ON
= {
x : x is an ordinal}
(3.20)
Theorem 3.2.8
[Transfinite Induction on ON]. If C ⊂ ON and C ≠ Ø, then C
has a least element.
Proof:
Fix α ∈ C. If α is not the least element of C, let β be the least element
of
α
∩
C.
Then
β
is the least element of
C.
Theorem 3.2.9 [Transfinite Recursion on ON].
If F : V → V, then there exists
a unique G : ON
→ V such that
Proof:
For uniqueness, if
G
1
and
G
2
both satisfy Eq. (3.21), we can show that
by transfinite induction on
α
.
(3.21)
To establish existence, we call g a δ-approximation if g is a function with
domain
g
and
(3.22)
As in the proof of uniqueness, if g is a
δ approximation and g' is a δ
-
'-
approximation, then
Next, by transfinite induction on
δ
, we can show that for each δ there is a δ
-approximation (which then is unique).
Now, let
G
(
α
) be the value g
(
α
), where g is the δ
-approximation for some
δ
>
α
.
A useful application of recursion is in defining ordinal exponentiation: Let α
and
β
be two ordinals. Then
α
β
is defined by recursion on β by
(1)
(2)
(3)
If β is a limit,
As in Chapter 2, 1–1 functions are used to compare the size of sets. Generally,
if A can be well-ordered, then A
α
for some α (Theorem 3.2.4), and there is
then a least such
α, which we will call the cardinality of the set A, denoted by
⏐A
⏐.
In any statement involving
⏐
A
⏐,
we imply that
A
can be well-ordered. Under
the Axiom of Choice,
⏐
A⏐ is defined for every set A. Regardless of the Axiom of
Choice,
⏐
α⏐
is defined and is ≤ α for every ordinal α.

Axiomatic Set Theory
73
Theorem 3.2.10.
If
⏐
α
⏐ ≤ β ≤ α, then ⏐
β
⏐ = ⏐
α
⏐.
Proof:
β ⊂ α
implies
⏐β⏐ ≤ ⏐α⏐
, and
α
~
⏐α⏐ ⊂ β
, so ⏐α⏐ ≤ ⏐β⏐
. Thus, by
Bernstein’s equipollent theorem in the previous chapter, we have
⏐α⏐
=
⏐β⏐
.
Theorem 3.2.11. If n ∈ ω, then
(1)
n
n
+ 1.
(2)
∀α ( α ~ n → α = n).
Proof:
Statement (1) can be proved by induction on
n
and (2) follows by using
Theorem 3.2.6.
Corollary 3.2.1.
ω
is a cardinal and each n
∈ ω
is a cardinal.
A set
A
is finite if
⏐
A
⏐
<
ω
and to be countable if
⏐
A⏐ ≤ ω. Infinite means not
finite. Uncountable means not countable.
Cardinal multiplication and addition are defined in the following. They must
be distinguished from ordinal multiplication and addition. Let
κ and λ be two
cardinals we define
Theorem 3.2.12.
For
Proof:
First show n + m < ω by induction on m. Then show n · m < ω by
induction on m. The rest follows from Theorem 3.2.11 (2).
Theorem 3.2.13.
Every infinite cardinal is a limit ordinal.
Proof: If κ is an infinite cardinal and κ = α + 1, then since 1 + α = α,
κ = ⏐κ⏐ = ⏐
1 +
α
⏐
=
⏐
α
⏐
.
This contradicts the definition of
κ
.
.
Theorem 3.2.14. If
κ is an infinite cardinal, κ × κ = κ
Proof: We prove the theorem by transfinite induction on κ. Assume this
holds for smaller cardinals. Then for
α < κ
,
⏐α × α⏐
=
⏐α⏐ ⊗ ⏐α⏐
<
κ
. Define a
well-ordering on
κ × κ by (α
,
β
)
(γ,
δ
)
if and only if
precedes
lexicographically]
(3.23)
Each has no more than
predecessors under the ordering
, so type
whence
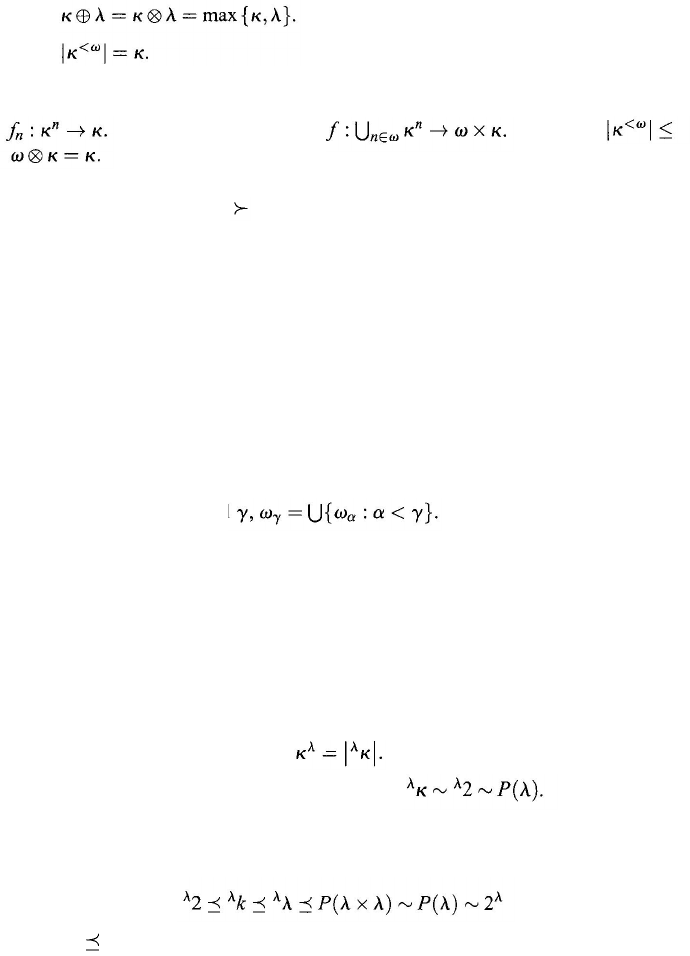
74
Chapter 3
Corollary 3.2.2. Let κ and λ be infinite cardinals then
(1)
(2)
Proof:
For (2), use the proof of Theorem 3.2.13 to define a 1–1 mapping
This gives a 1–1 mapping
Therefore,
Theorem 3.2.15.
∀α∃κ
(κ
α
and
κ
is a cardinal).
Proof:
Assume α ≥ ω. Let W =
{H : H
∈ P(
α × α
) and H well-orders α }.
Let S = {type(
H
) : H ∈ W}. Then
∪
S is a cardinal > α.
Let α be an ordinal and α
+
the least cardinal > α. A cardinal number κ is a
successor cardinal if there exists some ordinal
α such that κ = α
+
. The cardinal
κ is a limit cardinal if κ > ω and is not a successor cardinal. Now, the sequence
of transfinite cardinals
ℵ
α
=
ω
α
is defined by transfinite recursion on
α
by
(1)
ω
0
= ω.
(2)
ω
α
+1
= (ω
α
)
+
.
(3) For any limit ordinal
Theorem 3.2.16.
(1)
Every infinite cardinal is equal to ω
α
for some α .
(2)
α
<
β →ωα < ωβ.
(3)
ω
α
is a limit cardinal if and only if α is a limit ordinal.
(4)
ω
α
is a successor cardinal if and only if α is a successor ordinal.
We now turn to cardinal exponentiation. Let
A
B
=
B
A = {ƒ : ƒ is a function ∧
D
(ƒ) = B ∧ R
(ƒ)
⊂
A
}.
We define
Theorem 3.2.17. If λ ≥ ω and 2 ≤ κ ≤ λ
,
then
Proof:
λ
2 ~ P(λ) follows by identifying sets with their characteristic func-
tions. Then
where XY implies that there exists a 1–1 function from X into Y.
(3.24)
Cardinal exponentiation is not the same as ordinal exponentiation. For exam-
ple, the ordinal 2
ω
is ω
, but the cardinal 2
ω
= ⏐P(ω)⏐> ω .
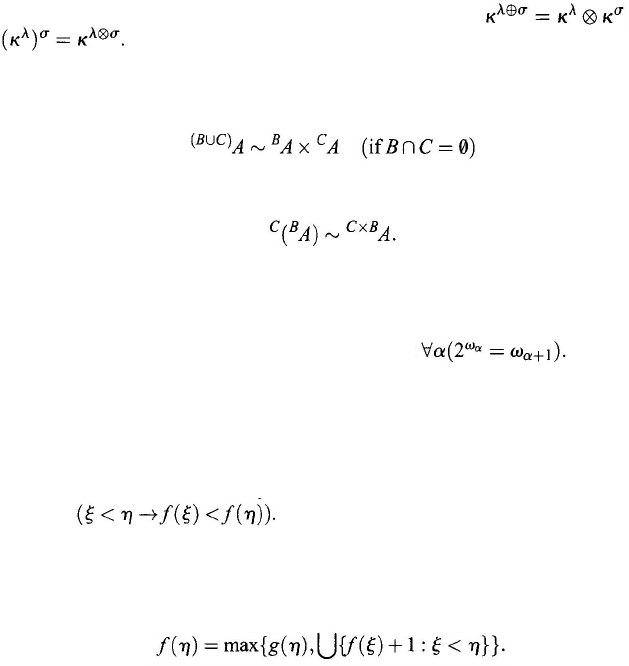
Axiomatic Set Theory
75
Theorem 3.2.18. If κ , λ , and σ are any cardinals, then
and
Proof:
We can check that
and
The Continuum Hypothesis (CH) is the conjecture that 2
ω
= ω
1
. The Gener-
alized Continuum Hypothesis is the conjecture that
If α and β are ordinals and ƒ : α → β is a mapping. The mapping ƒ maps α
cofinally if D
(ƒ) is unbounded in
β
; i.e.,
∀
b ∈ β∃
a
∈
D
(ƒ)(
b
≤
a
). The cofinality
of
β
, denoted by cf(
β
), is the least α such that there is a mapping from α cofinally
into
β
. Therefore, cf(
β
) ≤ β; if β is a successor, cf(
β
) = 1.
Theorem 3.2.19. There is a cofinal mapping ƒ : cf(
β) → β which is strictly in-
creasing
Proof: Let g : cf(β) → β be any cofinal mapping, and define a mapping ƒ
recursively by
Theorem 3.2.20. If α is a limit ordinal and ƒ : α → β is a strictly increasing
cofinal mapping, then cf(
α) = cf(
β
).
Proof:
cf(
β
) ≤ cf(α) follows by composing a cofinal mapping from cf(
α
)
into α with the mapping ƒ. To show cf(α) ≤ cf(
β
), let g : cf(β
)
→ β
be a cofinal
mapping, and let h(ξ) be the least η such that ƒ(η) > g (ξ ); then h : cf(β) → α is
a cofinal mapping.
Corollary 3.2.3. cf(cf(β)) = cf(β).
An ordinal
β is regular if β is a limit ordinal and cf(
β
) = β
. Thus, Corollary
3.2.3 implies that cf(
β
)
is regular for all limit ordinals
β
.
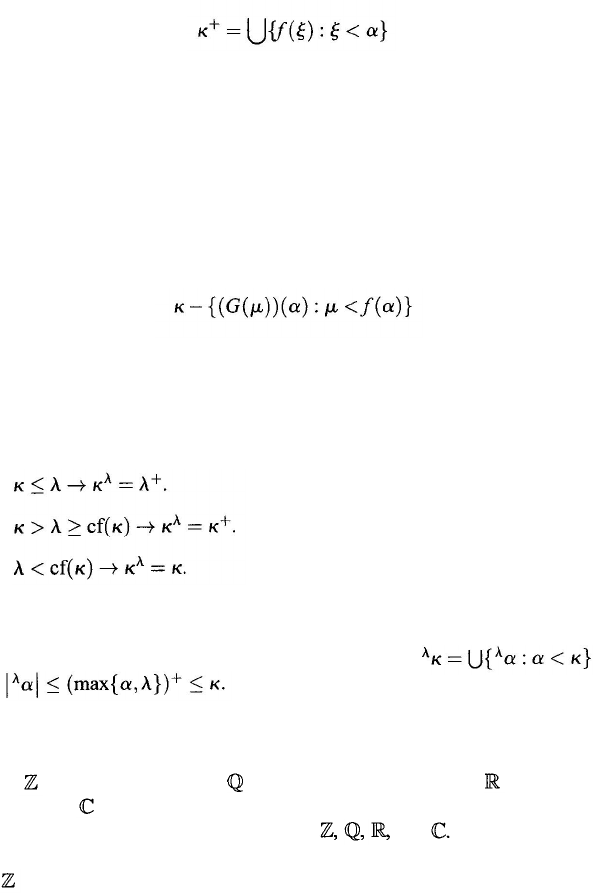
76
Chapter 3
Theorem 3.2.21.
If an ordinal
β
is regular, then
β
is a cardinal.
Theorem 3.2.22. κ
+
is regular.
Proof:
If ƒ mapped
α
cofinally into
κ
+
for some α < κ
+
, then
(3.25)
but the union of
≤ κ
sets each of cardinality
≤ κ
must have cardinality
≤ κ ⊗ κ
=
κ
by Theorem 3.2.14.
Theorem 3.2.23
[König’s Theorem].
If κ is infinite and cf(κ
)
≤ λ
, then κ
λ
>
κ .
Proof:
Fix a cofinal mapping ƒ : λ → κ
. Let
G
:
κ→
λ
κ
. We show that G
cannot be an onto mapping. Define h :
λ → κ so that h(α) is the least element of
(3.26)
Then h
∉ R
(
G
).
Theorem 3.2.24. Assume AC and GCH. Let κ and λ ≥ 2 and at least one of them
be infinite. Then
(1)
(2)
(3)
Proof:
(1) follows from Theorem 3.2.17. For (2),
κ
λ
> κ by Theorem 3.2.23,
but
κ
λ
≤ κ
κ
=2
κ
=
κ
+
. For (3), λ < cf(κ) implies that
each
and
We conclude this section by showing that all of classical mathematics can be
built upon ZFC.
Let
be the ring of integers,
the field of rational numbers, the field of real
numbers, and the field of complex numbers. It suffices to show that there is a
way, based on ZFC, to construct the sets of
and
Any reasonable way
of defining these sets from the natural numbers will do, but for definiteness we
take =
ω × ω/ ~, where (n,
m
) is intended to represent n – m the equivalence
relation ~ is defined by the following: (
a,b
) ~ (
c,d
) if and only if a + d = c + b
.

Axiomatic Set Theory
77
is the set of equivalence classes of the relation ~, and operations + and · are
defined as follows:
(3.27)
(3.28)
where [(
a
,
b)] is the equivalence class of the relation ~ containing (
a
,
b).
Let y
where (
x
,
) is intended to represent x/
y
, and
So is the
set of left sides of all Dedekind cuts. with field operations defined in
the usual way.
We will need the following definitions.
(a)
(b)
3.3. Families of Sets
For an infinite cardinal κ we say that two sets X and Y are k -disjoint if
Theorem 3.3.1.
If κ
≥
ω
0
and
⏐
A
0
⏐
=
κ,
then there exists S
0
⊂
p
(A
0
)
of power
κ
+
consisting of m-disjoint sets and such that A
0
=
S
0
.
Proof: It will be sufficient to find just one set A which can be decomposed as
in the theorem and has power
κ. A 1–1 mapping of A onto A
0
will then enable us
to obtain the desired decomposition of A
0
.
Let
κ
=
ℵ
α
and
. Two functions
ƒ, g
in
F
(conceived as sets of ordered
pairs) are
ℵ
α
-disjoint if
We will construct a sequence of type ω
α+1
of
ℵ
α
disjoint functions. To carry
out this construction we need the following lemma.
Lemma 3.3.1.
If
ϕ
is a transfinite sequence of type
γ < ω
α+1
with range contained
in F, then there exists a function ƒ ∈ F which is ℵ
α
-disjoint from each term ϕ
ξ
of
the sequence.
Proof of lemma:
To see this we notice that the range of
ϕ has power
≤ ℵ
α
and thus can be represented as the range of a function Φ : ω
α
→ F. If ξ <
Let ƒ (
ξ
) be the first ordinal in
Then ƒ
∈
F
which is
ℵ
α
-disjoint from every
Φ
η
, because
can hold
only if
η ≥ ξ
.
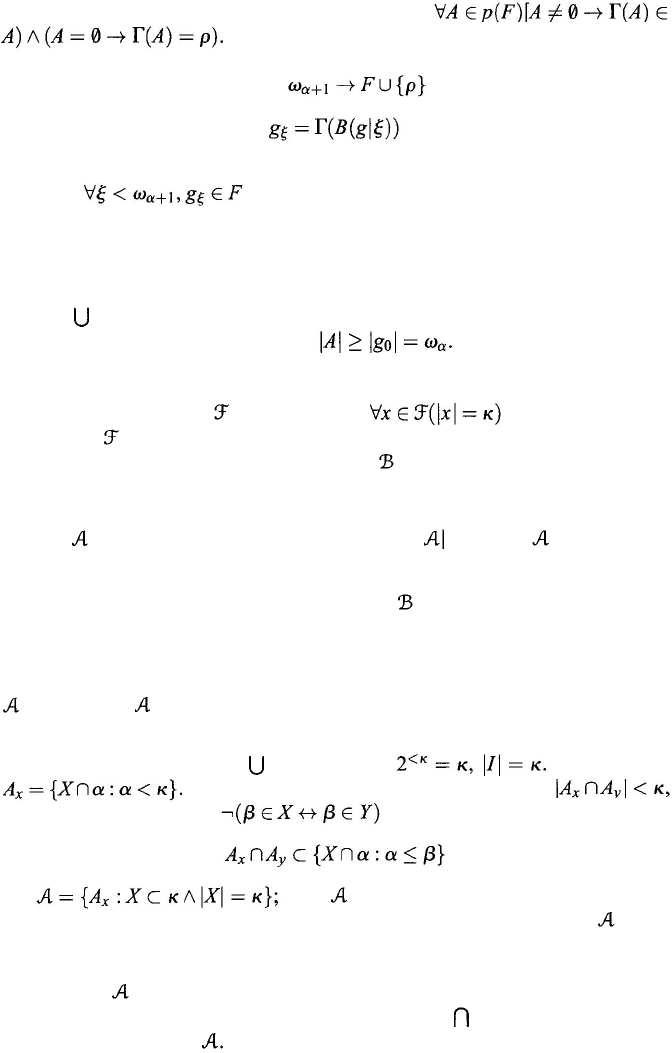
78
Chapter 3
Let Γ : p(
F
)
→
F
∪
{
ρ
}, where ρ ∉ F, such that
For each transfinite sequence
ϕ denote by B(ϕ
) the
set of all functions in F which are ℵ
α
-disjoint from all terms of ϕ. By transfinite
induction, we obtain a function
g
: satisfying the equation
(3.29)
for each
ξ <
ω
α
+1
.
Thus, and is
ℵ
α
-disjoint from all
g
η
, η < ξ, which belong
to F, provided that such functions exist; otherwise g
ξ
= ρ.
We claim that g
ξ
≠ ρ for each ρ < ω
α
+1
. Otherwise there would be a smallest
γ < ω
α
+1
(
g
γ
= ρ
) and g
⏐γ would be a sequence satisfying the assumptions of
Lemma 3.3.1. This contradicts the assumption that
ρ
∉
F. Thus, ⏐
R
(
g
)
⏐ =
ω
α
+1.
Let
A
=
R (
g
). Since each element of A is an ordered pair of ordinals <
ω
α
, we
infer that
⏐
A
⏐
≤ ω
α
; on the other hand,
Thus,
⏐
A
⏐ = ω
α
.
For an infinite cardinal κ two sets x, y ⊂ κ are almost disjoint if ⏐
x
∩
y
⏐ < κ.
An almost disjoint family
⊂
p
(κ)such that
and any two distinct
elements of
are almost disjoint. A maximal almost disjoint family is an almost
disjoint family with no almost disjoint family
properly containing it.
Theorem 3.3.2. Let κ ≥ ω
0
then
(a)
If
⊂
p
(
κ) is an almost disjoint family and
⏐
⏐
= κ
, then
is not
maximal.
(b)
There is a maximal almost disjoint family
⊂
p
(
κ) of cardinality ≥ κ
+
.
The proof follows from that of Theorem 3.3.1.
Theorem 3.3.3. If κ ≥ ω and 2
<κ
0
= κ, then there exists an almost disjoint family
⊂
p
(κ
)
with
⏐
⏐
= 2
κ
.
Proof: Let I = { x
⊂ κ : x < κ}. Since If X ⊂ κ, let
If
⏐X
⏐
=
κ,
then
⏐
A
x
⏐
=
κ
also. If
X
≠
Y,
then
since if we fix
β
such that
then
(3.30)
Let then
⏐
⏐
= 2
κ
and is an almost disjoint family
of subsets of I. If we let ƒ be a 1–1 function from I onto
κ,{ƒ(A): A ∈ } is an
almost disjoint family of 2
κ
subsets of κ.
A family
of sets is called a ∆
-system, or a quasi-disjoint family, if there is a
fixed set r, called the root of the ∆
-system, such that a
b = r whenever a and b
are disjoint members of
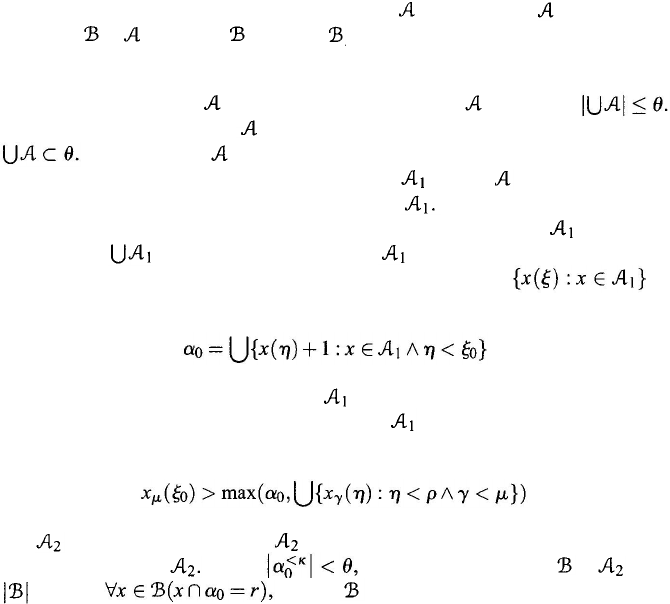
Axiomatic Set Theory
79
Theorem 3.3.4.
(
∆-System Lemma). Let κ be an infinite cardinal. Let θ > κ be
regular and satisfy
∀α
<
θ
(
⏐α
<κ
⏐ < θ
).
Assume ⏐ ⏐≥θ
and
∀
x
∈
(
⏐
x
⏐
<
κ
)
then
there is a
⊂
such that
⏐
⏐ = θ
and
forms a ∆
-system.
Proof:
By shrinking
if necessary, we may assume
⏐
⏐
=
θ.
Then
Since what the elements of
are as individuals is irrelevant, we may assume
Then each x
∈ has some order type < κ as a subset of θ. Since θ is
regular and
θ > κ, there is some ρ < κ such that
= {x
∈
: x has type ρ
} has
cardinality θ. We now fix such a ρ and deal with
For each
α
<
θ, ⏐α
<κ
⏐
<
θ
implies that fewer than
θ
elements of are subsets
of
α.
Thus,
is unbounded in θ. If x ∈ and ξ < ρ, let x (
ξ
) be the ξ
th
element of x. Since θ is regular, there is some ξ such that
is
unbounded in θ. Now fix ξ
0
to be the least such ξ (
ξ
0
may be 0). Let
(3.31)
Then α
0
< θ and x(
η
) < α
0
for all x ∈ and all η < ξ
0
.
By transfinite recursion on µ < θ, pick x
µ
∈
so that
x
µ
(
ξ
0
) >
α
0
and
x
µ
(ξ
0
)
is above all elements of earlier x
γ
; i.e.,
(3.32)
Let = {x
µ
: µ < θ}. Then ⏐⏐ = θ and x
∩
y ⊂ α
0
whenever x and y are
distinct elements in Since
there is an r ⊂ α
0
and ⊂ with
=
θ and whence forms a ∆-system with root r.
Under the assumption of CH or GCH, we calculated many exponentiations of
cardinals in Section 3.2. If we now assume that CH fails, questions arise about the
various infinite cardinals κ < 2
ω
. For example, we have
Question 3.3.1. If
κ < 2
ω
, does 2
κ
= 2
ω
?
Question 3.3.2. If κ < 2
ω
, does every almost disjoint family A ⊂
p
(
ω
) of size κ
fail to be maximal?
Since the answer to these questions is clearly “yes” when
κ = ω, they are only
of interest for
ω < κ < 2
ω
. For such κ, it is known by the method of forcing that
neither question can be settled under the axioms ZFC +
¬
CH. In the following we
show how these questions can be settled by using a new axiom, called Martin’s
axiom. Martin’s axiom is known to have numerous important consequences in
combinatorics, set-theoretic topology, algebra, and analysis. For examples other
than those given here, please consult (Martin and Solovay, 1970; Rudin, 1977;
Shoenfield, 1975).
