Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

204

Chapter 9

Proof:

(i) follows from the definition of

-continuity of mappings and Example

9.1.1.

For (ii), let (X, +) be a group. A system (X

) is defined as follows: R = {

}

and

The system (X,R) will be identified with

the group (X, +), and the relation r

with +.

Let

,i =

1,2, be two groups and

→ S

an S

-continuous

mapping. Then

Thus, for any x, y, and z ∈ M

, if x

y = z, then

(

)

(

y) = h

(

z) This implies that h is a homomorphism from S

into S

The proof of (iii) is a modification of that of (ii) and is omitted.



Theorem 9.2.4.

A bijection h

→ S

is a similarity mapping iff h

→ S

and

–1

: S

→ S

are S-continuous.

The proof is straightforward and is left to the reader.

Theorem 9.2.5.

Suppose that

ƒ :

→ S

and g : S

+ S

are S-continuous map-

pings. Then the composition g

ƒ : S

→

is also S-continuous.

Proof: For each relation r in the system S

, from the hypothesis that the

mapping g is S

-continuous we have

(9.24)

From the hypothesis that the mapping ƒ is S-continuous, it follows that

Therefore, from Eq. (9.25),

Thus,

ƒ is S

-continuous.



9.3. Constructions of Systems

(9.25)

Let

a set of systems such that M

for any

if I = {1,2, . . . ,n} is finite, is defined to be the system

(9.26)

distinct i and j ∈ I. The free sum of the systems S

, denoted ⊕

{

: i ∈ I} or

General Systems: A Multirelation Approach

205

The concept of free sums of systems can be defined for any set {S

: i ∈ I

}

of systems such that the collection of all object sets of the systems in the set

consists of not necessarily pairwise disjoint sets. To show this, we simply take a

set {

∈

} of systems with pairwise disjoint object sets such that

is similar

to S

, for each

∈

and define

(9.27)

Up to a similarity, the free sum of the systems S

is unique. Therefore, it can

be assumed that any set of systems has a free sum (uniquely determined up to

a similarity), but in the proofs of some theorems in the future it will be tacitly

assumed that the set under consideration consists of systems with pairwise disjoint

object sets.

A system S = (

M,R

) is an input–output system if two sets X and Y are given

such that

and for each relation

∈

there are nonzero ordinals

(r)

and m =

(

) such that r ⊆ X

× Y

The sets X and Y are called the input space

and the output space of the system S, respectively.

Proposition 9.3.1.

Let S

and S be two similar systems. If S is a free sum of

some systems, then so is S

Proof: Suppose that S

⊕

∈

}, where {S

∈

} is a set of systems

= (M

), and h : S

→ S

is a similarity mapping. Then

(9.28)

because for each i ∈ I, and for each r ∈ R

there exists a relation

∈ R

for some

∈

such that

(

) = r.



Theorem 9.3.1.

Suppose that

{

= (M

) :

∈

} is a set of systems, where I

is an index set. Then the free sum

⊕

{

∈

} is an input–output system iff each

system S

= (

) is an input–output system, i ∈ I.

Proof:

Necessity. Suppose that

⊕

{

: i ∈ I} is an input–output system with

there are nonzero ordinals

(

) and m = m

(

) such that r ⊆ X

. Hence,

is an input–output system with input space M

X and output space M

Sufficiency. Suppose that

= (

) is an input–output system with input

space

and output space

. Then for each relation r in ⊕

{

: i ∈ I

}, there exists

an i ∈ I such that r ∈ R

; therefore,

(9.29)

input space X and output space Y. Then for any fixed i

∈ I and any relation r ∈ R

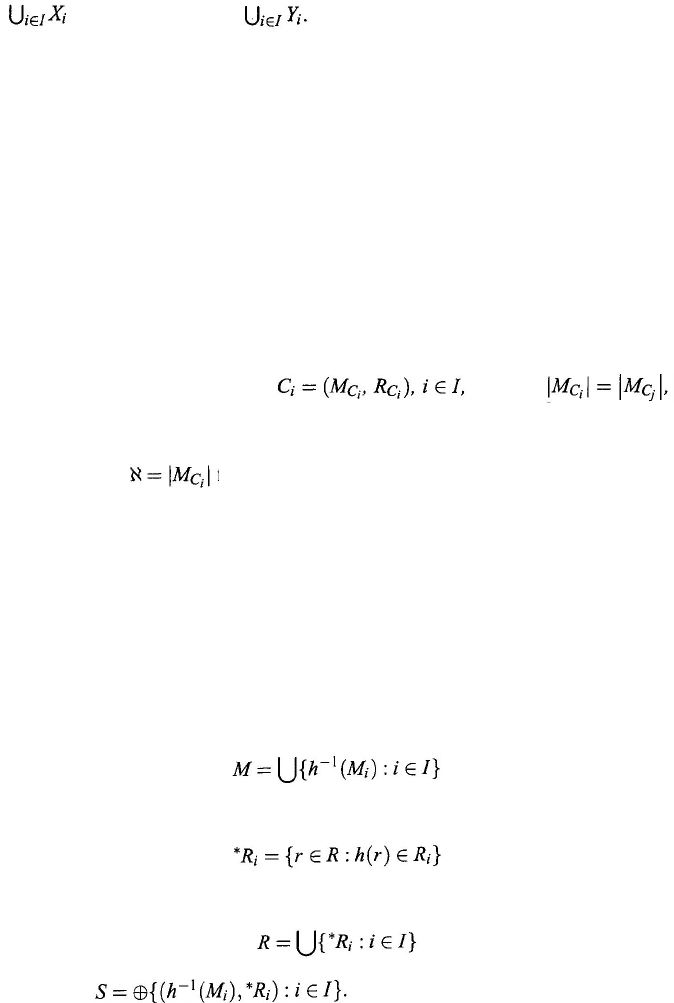
206

Chapter 9

Theorem 9.3.2.

If a system S is embeddable in the free sum

⊕

{

∈

} of some

systems S

, then S is also a free sum of some systems.

The proof is straightforward and is omitted.

Theorem 9.3.3.

If the free sum

⊕

{

∈

} of nontrivial systems S

is a central-

ized system, then each S

is centralized, for i ∈ I.

Proof: The theorem follows from the fact that each center of the free sum

⊕

{

∈

} is a center of each system S

, i ∈ I.



Theorem 9.3.4.

Suppose that

{

∈

} is a set of centralizable systems such

that each system S

has a center

and that

for all i and j ∈ I. Then the free sum ⊕

{

∈

} is a centralizable system.

Proof:

Let

for some i

∈

Then the system (

ℵ

,Ø) is embeddable in

each object in the free sum

⊕

{

∈

}. Theorem 9.2.2 implies that the free sum

is centralizable.



It is easy to construct an example to show that the free sum of two centralized

systems may not be a centralizable system.

Theorem 9.3.5.

Let h

→ ⊕

{

∈

} be a homomorphism. Then the system

S is also a free sum of some systems.

Proof:

Suppose that S = (M,R) and S

= (

) for each i ∈ I. Then

(9.30)

Define

(9.3 1)

From the hypothesis that h is a homomorphism it follows that

(9.32)

Therefore,



Hence, the free sum ⊕

{

∈

} is an input–output system with input space

and the output space



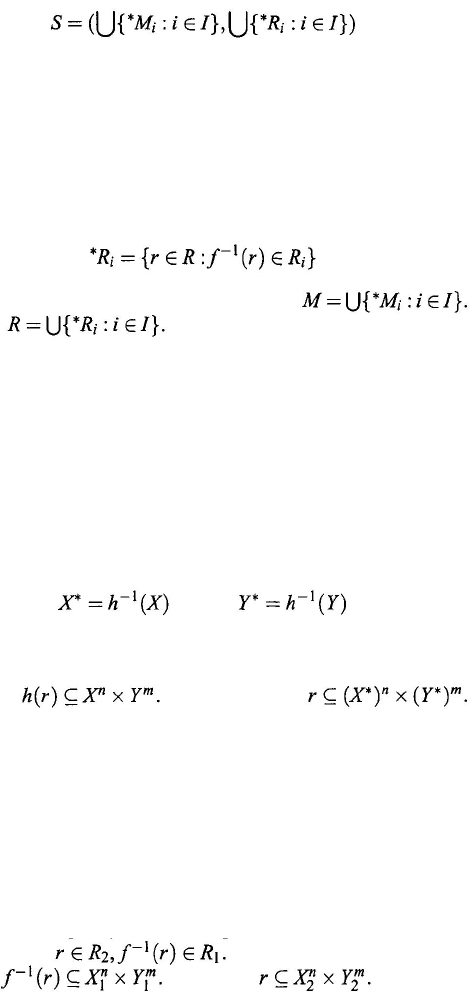
General Systems:

A Multirelation Approach

207

Theorem 9.3.6.

Let

ƒ :

⊕

{

∈

} → S be an onto S-continuous mapping. Then

there are partial systems

∈

} of S such that

(9.33)

where

= (*

, *R

), for each i ∈ I, and ƒ : S

→

is S-continuous.

Proof:

For each

∈

we define a system *

= (*M

, *R

) as follows:

= ƒ (

)

(9.34)

and

(9.35)

From the hypothesis that ƒ is surjective, it follows that

Since ƒ

is S

-continuous,

Then Eq. (9.33) follows and the

-continuity

of the mapping ƒ : S

→

follows from Eq. (9.35).



Question 9.3.1. Under what conditions will the system S in Theorem 9.3.6 be a

free sum of some systems?

Theorem 9.3.7.

Suppose that h

→

is a homomorphism from a system S

into an input–output system S

. Then S

is also an input–output system.

Proof:

Suppose that

has input space X and output space Y. Define

and

(9.36)

Then S

is an input–output system with input space X* and output space Y*. In

fact, let r be a relation in S

. Then h

(

) ∈ R

. Hence, there are nonzero ordinals

n and m such that This implies that



Theorem

9.3.8.

Let

ƒ :

→

be an S-continuous mappingfrom an input–output

system S

into a

system S

. Then S

is also an input–output system.

Proof:

Suppose that

has input space X

and output space Y

. Define

= ƒ (

)

and

= ƒ (

)

(9.37)

Then S

is an input–output system with input space X

and output space Y

. In

fact, for each relation Hence, there are nonzero ordinals n

and m such that Therefore,



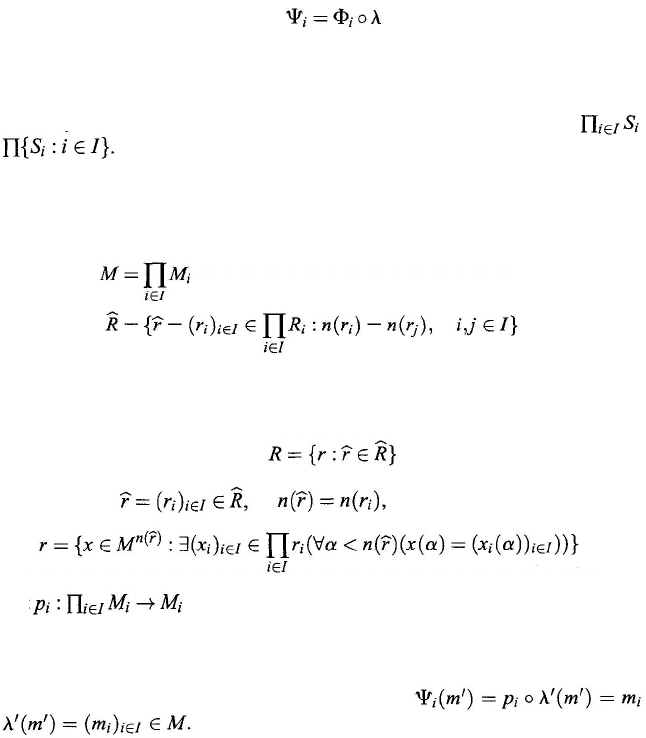
208

Chapter 9

Let S

and S

be two systems. We define

Hom(

, S

) = {

h : S

→

is a homomorphism}

(9.38)

Suppose that {

∈

} is a set of systems. A system

= (

M,R) is a product of

the systems

if there exists a family of homomorphisms {

∈

Hom(

S,S

) : i ∈ I

}

such that for each system S' and a family {Ψ

∈

Hom(

S', S

) : i ∈ I}, there exists

a unique homomorphism

λ ∈

Hom(

S',S) so that

(9.39)

for all i

∈ I.

Theorem 9.3.9.

For each set

{

: i ∈ I } of systems, a product of the systems

always exists, which is unique up to a similarity and denoted by or

Proof:

For the set of systems {

: i ∈ I}, we define a system S = (

M,R

) as

follows:

(9.40)

(9.41)

(9.42)

and

(9.43)

where for any let

for

∈

and

(9.44)

Let

be the projection for each i ∈ I. Then p

∈

Hom(

S,S

We now suppose that S' = (M',R'

) is a system and {

∈

Hom(

S',S

) : i ∈ I}.

Define a mapping

→

as follows: For any object

∈

M',

(

) = {

(

) :

∈ I

}

∈

It then can be shown that

λ ∈

Hom(

S',S

If λ ' is another such homomorphism, then if

Thus,

λ' = λ as mappings from the object set M' into

the object set M. Therefore, they induce the same homomorphism. Therefore, S

is a product of the systems S

∈



Let {S

: i ∈ I} be a set of systems. A system S = (M,R) is a Cartesian

product of the systems S

if there exists a family of S-continuous mappings {p

General Systems: A Multirelation Approach

209

→

: i ∈ I} such that for each system S' and a family {

: S' → S

: i ∈ I} of

-continuous mappings, there exists a unique

-continuous mapping λ : S' → S so

that q

= p

for each

∈

Theorem 9.3.10. For each set {S

: i ∈ I} of systems, a Cartesian product of

the systems S

always exists, which is unique up to a similarity and denoted by

Proof:

Let

= (M

, R

) for each

∈

Define a system

= (

M,R) as follows:

(9.45)

and

(9.46)

and define mappings

: S → S

by letting

for any

for each i ∈ I. Then it can be readily checked that each mapping p

: S → S

S-continuous.

Let S' = (

M',R'

) be another system, and {

: S' → S

: i ∈ I} a family of

S-continuous mappings. Define a mapping

λ : S' → S by

(9.47)

for each object m' ∈ M'. Then λ is S-continuous. In fact, for an arbitrary relation

∈ R, let r

∈ R

be a relation such that

Then

To complete the proof, we show that all Cartesian products of the systems S

are similar to each other.

210

Chapter 9

Figure 9.1.

Uniqueness of the Cartesian product.

Let S* = (

*,R

*) b

another Cartesian product of

, i ∈ I. Then there are S-

continuous mappings

→

and

: S* → S such that the diagram (Fig. 9.1)

commutes for each i

∈ I. That is, for each i ∈ I, we have

(9.48)

It suffices to show that

(9.49)

and

(9.50)

for each m ∈ M and m

∈

*. In fact, Eq. (9.49) implies that the mapping λ

1–1, and Eq. (9.50) implies that

is 1–1;

= λ

–1

and λ

–1

. Therefore,

and

are similarity mappings.

Now, we prove Eqs. (9.49) and (9.50). For Eq. (9.49), let

then

Therefore,

A similar argument shows

Eq. (9.50).



The reason why the system S in Theorem 9.3.10 is called a Cartesian product

of the systems S

is that when S

are topological spaces, S is the Cartesian product

of the spaces S

. The system

{

∈

} in Theorem 9.3.9 is the box product of

the spaces S

. When the systems

are groups,

{

∈

} in Theorem 9.3.9 is

the direct sum of the groups S

. The mappings

in the proofs of Theorems 9.3.9

and 9.3.10 are called projections from the product systems into the factor systems.

General Systems: A Multirelation Approach

211

Let

be a set of systems such that each object in any one system

the set is a system again. The 1-level product system, denoted by

is defined by where the object set M and the relation set

R are defined as follows: There exists a bijection such that

(9.5 1)

and

(9.52)

The 1-level Cartesian product, denoted by is the system (M, R

)

defined by the following: There exists a bijection such that

(9.53)

and

(9.54)

Theorem 9.3.11. Let be a set of centralizable systems. Then the

1-level

product system

and the 1-

level Cartesian product system

are also centralizable systems.

Proof:

For each

∈

suppose that is a center of the system

For the 1-level product system it suffices by Theorem 9.2.2 to show

that the product system is embeddable in each product

for all

From Theorem 9.2.2 we will not lose generality by assuming that each system

is embeddable in each object in M for i ∈ I. For each

Let and

be an embedding mapping. Then the product

mapping

(9.55)

defined by

(9.56)

for each object is an embedding mapping. In fact, first,

the product mapping is 1–1, because if and

are two distinct

212

Chapter 9

objects in

there exists an

∈

such that Therefore, since

is an embedding mapping it follows that

Therefore,

(9.57)

Second, for each relation

in there exists a relation

such that

(9.58)

In fact, for each relation

in there exist relations

for each

i ∈ I, such that

for all

∈

and

(9.59)

From the hypothesis that each h

is an embedding mapping, it follows that there

exists a relation

for each i ∈ I, such that

(9.60)

Equation (9.60) implies that

for each i

∈ I. Define a relation s in

as follows:

(9.61)

We now show that s satisfies Eq. (9.58). In fact,

(9.62)

General Systems: A Multirelation Approach

213

where

for each α < n

(

) and i ∈ I.

We complete the proof of the theorem by observing that

(9.63)

The centralizability of the 1-level Cartesian product system

can be proved in a similar way.



Theorem 9.3.12. A mapping h from a system S = (M, R) into a Cartesianproduct

system is S-continuous iff the composition p

h is S-continuous

for each i

∈ I.

Proof:

Necessity. Suppose that

is S

-continuous. From

Theorem 9.2.5 and the proof of Theorem 9.3.10, it follows that each composition

h is S-continuous, i ∈ I.

Sufficiency. Suppose that each composition

h is S-continuous, i ∈ I. Let

for each i

∈ I. For each relation r in there exist an

∈ I and a relation r

∈

satisfying that

Therefore,

(9.64)

This implies that i.e., h is S

-continuous.



Theorem 9.3.13. A mapping h from a system S = (M, R) into a product system

is a homomorphism iff the composition p

h is a homomorphism for

every i ∈ I.

Proof: Necessity. Suppose that is a homomorphism.

From the fact that each projection is a homomorphism, it

follows that p

h is a homomorphism for every i ∈ I.

Sufficiency. Suppose that

h is a homomorphism for every i ∈ I. Let r ∈ R.

We need to show that h(

) is a relation in For each i ∈ I we have

since p

h is a homomorphism. Therefore,

(9.65)