Yi Lin. General Systems Theory: A Mathematical Approach
Подождите немного. Документ загружается.


234
Chapter 9
Hence, by induction we have showed that S
np
= S for each integer n < 0.
Combining cases 1 and 2 completed the proof.
Corollary 9.5.1. If a system S over a group is periodic, there then is a positive
period for S.
A linked system {S, l
ts
,
T
} over a group is periodic, if S is a periodic system
over a group with a period such that for any t, s
∈ T satisfying
s
≥ t. This element in T is called a period of the linked system {S, l
ts
,
T
}.
Theorem 9.5.7. If is a period of a linked system {S, l
ts
,
T
} over a group, then
so is n for each integer n
≠ 0.
The proof is straightforward and is omitted.
Theorem 9.5.8. Suppose that a linked system {S, l
ts
,T} over a group is periodic
with > 0 as a period. Then the hierarchy
is similar to the
hierarchy
for any integer n.
Proof:
First we show that n < (n + 1) for each integer n. In fact, if
n
≥ (
n
+ 1)
for some integer n, then
(9.167)
This contradicts the hypothesis that > 0.
Second, we define a mapping
by
(9.168)
Then
φ is a similarity mapping from the ordered set onto the ordered
set We next define mappings
for each
as
identity mappings. Then {
φ
,ƒ
x
}
is a similarity mapping from the hierarchy H into
the hierarchy K.
Corollary 9.5.2. In Theorem 9.5.8, the ordered sets
and
can be
replaced by each of the following pairs:
Generally, for a periodic system {S, l
ts
,T } over a group, the hierarchies
and are not similar.

9.6. Controllabilities
The concept of controllability of systems was originally introduced as a prop-
erty of input–output systems. The main idea behind the concept says that an
input–output system S is controllable provided that, if we need to obtain some
output of the system with certain predetermined properties, we then can find some
input such that the corresponding output satisfies the required properties. In this
section we study different concepts of controllability not only of input–output
systems but also of general systems.
Let S = ( M,R
) be an input–output system with input space
X
and output space
Y. In the following, the symbols (x,y) and
will be used congruently, where
and
We now define
(9.169)
(9.170)
(9.171)
(9.172)
(9.173)
(9.174)
(9.175)
for any i
∈ o
(
X
),
for any
j
∈
o
(
Y
),
and
and
Suppose V is a set and G a mapping such that
G
: Dom(
X) × Ran(Y
)
→
V
For an element v ∈ V, the system S is v -controllable relative to G if and only if
there exists a mapping cg : Dom(X
)
→
Dam(
X ) such that, for any x ∈ Dom( X),
there exists a y
x
∈ Ran(Y) such that
(9.176)
The mapping cg is called a control function of S.
General Systems: A Multirelation Approach
235
236
G
(cg(
x), y
z
) = v
Chapter 9
For example, suppose we are processing a chemical reaction. To reach a
collection of desired results (denoted by y
x
) which satisfy an assigned target
(denoted by v), we could choose various methods (denoted by x) for processing
the wanted results. But, in order to control the whole reaction procedure, we may
add relative materials [denoted by cg(x)] together with those “choices” we have
had. We would like to deem the “input” (the relative materials) as “control” for
the whole reaction procedure.
Theorem 9.6.1. For each element v
∈ V, the input–output system S is v-
controllable relative to the mapping G iff v
∈ G
(Dom(
X) × Ran(Y
)).
Proof: The necessity part of the proof follows from Eq. (9.176).
Sufficiency. Let v
∈ G
(Dom(
X) × Ran(Y)). Then there exists (x, y) ∈
Dom(
X) × Ran(Y) such that G(x, y) = v. Define a control function of S,
cg : Dom(X)
→ Dom(X), as follows: cg(w) = x for all w ∈ Dom(X). Then
for each w
∈ Dom(X) there exists y
w
= y ∈ Ran(Y) such that
G
(cg(
w), y
w
) = G(x, y) = v
Let
V'
⊂
V
be a subset. The input–output system
S
is controllable on
V'
relative
to G : Dom(X
)
×
Ran(
Y) → V iff there exists a mapping cg : Dom(X) → Dom(X
)
such that, for each
v
∈
V'
and any
x
∈
Dom(
X), there exists y
z
= y
(
v, x) ∈ Ran(Y
)
such that
(9.177)
The mapping cg is called a control function of S.
Theorem 9.6.2. For a subset V'
⊂ V, the input–output system S is controllable
on V' relative to the mapping G iff there exists an element x
∈ Dom(X) such that
G
({
x} × Ran(Y)) ⊃ V'.
Proof: Necessity. Let cg : Dom(X)
→ Dom(X) be a control function of
the system S. Then, for each v
∈ V' and each x ∈ cg(Dom(X)), there exists a
y
∈ Ran(Y) such that G(x, y) = v. Hence, G
(
x,
Ran(
Y
)) ⊃ V'.
Sufficiency. Suppose there exists an element x
∈ Dom(X) such that G
({
x } ×
Ran(
Y)) ⊃ V'. Define a control function cg : Dom(X) → Dom(X) by letting
cg(
w) = x for all w ∈ Dom(X). Clearly, each v ∈ V' and any w ∈ Dom(X), there
exists a y
∈ Ran(Y ) such that
G
(cg(
w), y) = G(x, y) = v
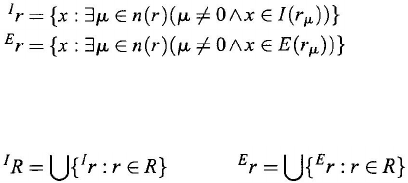
General Systems: A Multirelation Approach
237
Therefore, S is controllable on V' relative to G.
For V' ⊂ V, the input–output system S is collectively controllable on V'
relative to the mapping G : Dom(X
)
× Ran(Y) → V iff there exists a mapping
cg : Dom(X)
→ p
(Dom(
X)), where p
(Dom(
X)) is the power set of Dom(X), such
that for any v
∈ V' and any x ∈ Dom(X), there exists y = y
(
v, x) ∈ Ran(Y
) such
that
G
(z, y) = v
for some
z
∈
cg(
x
)
(9.178)
Theorem 9.6.3. For a subset V' ⊂ V, the input–output system S is collectively
controllable on V' relative to the mapping G : Dom(X
)
× Ran(Y) → V iff there
exists a nonempty subset A
⊆ Dom(X) such that G
(
A × Ran(Y)) ⊇ V'.
Proof: Necessity. Let cg : Dom(X)
→ p
(Dom(
X)) be a control function for
S. Then for any v
∈ V' and each x ∈ Dom(X), there exists a y ∈ Ran(Y ) such
that G
(
z, y) =
v for some z
∈ cg(x). Hence, there exists an x ∈ Dom(X) such that
G(cg(x)
× Ran(Y )) ⊇ V', where cg(x) ≠ Ø.
Sufficiency. Suppose there exists a nonempty subset A
⊆ Dom(X) such that
G
(
A × Ran(Y )) ⊇ V'. Let us define a control function cg : Dom(X) → p
(Dom(
X
))
as follows: cg(x) = A for all x ∈ Dom(X). Then for any v ∈ V' there exists
(
z, y) ∈ A × Ran(Y) such that G
(
z, y
) =
v. This implies that, for any v ∈ V' and
any x
∈ Dom(X), there exists y = y
(
v, x) ∈ Ran(Y ) such that G
(
z, y) = v. This
completes the proof of the theorem.
Examples can be given to show that not all systems are input–output systems.
In the following, we study the concept of controllability of general systems.
Suppose
S
= (
M, R
) is a general system. For any relation
r
∈
R
and any ordinal
number µ > 0, we define the µ-initial section of r, denoted by I(
r
µ
), as follows:
For any x
∈ I(
r
µ
) ⊂ M
µ
, there exists y ∈ M
v
such that (x, y) ∈ r, where v is a
nonzero ordinal number such that µ + v = n
(
r
) such that r ⊂ M
n(r
)
. We define
the µ-final section of r, denoted by E(r
µ
), as follows: for any x ∈ E(r
µ
) ⊂ M
v
,
there exists y
∈ I(
r
µ
) such that (
y, x) ∈ r.
Let
(9.179)
(9.180)
(9.181)
and
and
(9.182)

238
Chapter 9
If M
*
⊂ M,
and
(9.183)
are used to indicate all the elements in
I
R and all the elements in
E
R, respectively,
in which only the elements of M
*
appear as coordinates.
Let V be an another set and V'
⊂ V. The general system S is generally
controllable on V' relative to a mapping
(9.184)
if, for each v ∈ V', there exist a set W
v
, an
M
v
⊂ M, and a mapping
(9.185)
such that for each
u
∈
W
v
there exists a y
u
∈
E
R such that
for some (9.186)
The mapping
C
v
is called a control function of S.
The main idea of general controllability of systems is the following. Suppose
we are given a set of desired targets V. For each v
∈ V, there exists a set of
“commands” given to a system S so that S can realize the desired target v. When
S receives the commands, there will be some “well-organized” objects of S to
accomplish the task. Therefore, there should be some “receivers” and “accom-
plishers” in S such that the whole process of executing the task is under a good
control with a “fine” cooperation between the “receivers” and the “accomplishers.”
Theorem 9.6.4. Let S be a general system and V' ⊂ V a subset. Then S is
generally controllable on V' relative to a mapping iff there
exists a nonempty subset M
V'
⊂ V such that for some nonempty
Proof: Necessity. Suppose S is generally controllable on V' relative to G.
Then for each v
∈ V' there exist M
v
⊂ M and a nonempty A
v
such
that
(9.187)
Let
and
Then
(9.188)
and from Eq. (9.187) we have
G
(A ×
E
R) ⊃ V'.
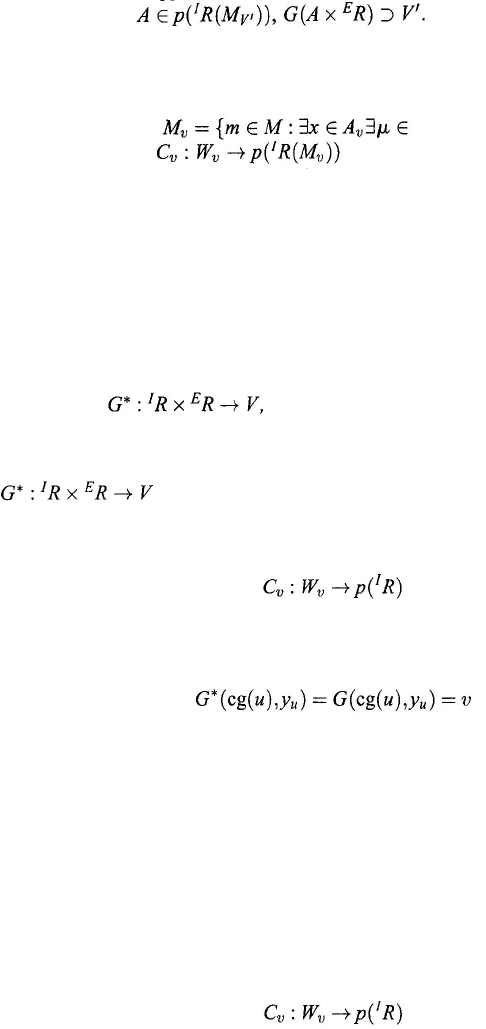
General Systems: A Multirelation Approach
239
Sufficiency. Suppose there exists a nonempty subset M
V'
⊂ M such that for
some nonempty
Thus, for each v
∈ V' there
are subsets A
v
⊂
A
and
B
v
⊂
E
R such that
G
(
A
v
× B
v
) = {v
}
(9.189)
Define
M
v
⊂ M by
ON (
m
=
x
µ
)}. Let W
v
be any
nonempty set and a mapping defined by C
v
(
u
) = A
v
for
each u ∈ W
v
. Then for each u ∈ W
v
there exists a y
u
∈
B
v
⊂
E
R such that
G(z,y
u
) = v
for some z
∈ C
v
(
u
)
This proves the assertion.
Proposition 9.6.1. Suppose that S = (M, R) is an input–output system with input
space X and output space Y, and that S is v-controllable relative to a mapping
G : Dom(X)
× Ran(Y) → V. Then S is generally controllable on {v} relative to
the mapping where G
*
is an extension of G.
Proof: Because Dom(X ) ⊂
I
R and Ran(Y ) ⊂
E
R, we can define extensions
for the mapping
G.
We now show the general controllability of S. For v ∈ {v} there exist a set
W
v
= Dom(X) and a mapping
(9.190)
defined by C
v
(
u
) = {cg(
u
)},
w
h
ere cg : Dom(X) → Dom(X) is a control function
for S. Hence, for each u
∈ W
v
there exists a y
u
∈ Ran(Y ) ⊂
E
R
such that
(9.191)
where cg(
u
) ∈ C
v
(
u
).
Proposition 9.6.2. Let V' ⊂ V be a subset such that an input–output system S =
(
M, R) is controllable on V' relative to a mapping G : Dom(X) × Ran(Y) → V,
where X and Y are the input and the output spaces of S, respectively. Then S is
generally controllable on V' relative to each extension G
*
of G.
Proof: For each v ∈ V' there exist sets W
v
= Dom(X) and M
v
= M and a
mapping
(9.192)

Chapter 9
240
defined by C
v
(
u
) = {cg(
u
)} for each u ∈ W
v
. Then for each u ∈ W
u
, there exists
y
u
= y
(
v, u
) ∈ Ran(Y ) ⊂
E
R such that
(9.193)
where cg(
u
) ∈ C
v
(
u
).
Proposition 9.6.3. Suppose that S = (M, R) is an input–output system with input
space X and output space Y such that S is collectively controllable on V' relative
to a mapping G
: Dom(
X) × Ran(Y) → V. Let
be an extension
of G. Then S is generally controllable on V' relative to G
*
.
Proof: For each v ∈ V' there exist sets W
v
= Dom(X) and M
v
= M and a
mapping
(9.194)
such that, for each
u
∈
W
v
, there exists y
u
= y (v, u) ∈
Ran(
Y ) ⊂
E
R such that
G
*
(
z, y
z
) = G(z,y
u
) = v
(9.195)
for some z
∈ C
v
(
u ) = cg(
u
).
Theorem 9.6.5. Suppose that h : S
1
= (
M
1
, R
1
) → S = (M, R
)
is an S-continuous
mapping from a system S
1
into a system S such that S is generally controllable on
V' relative to a mapping
Then S
1
is generally controllable on
V' relative to a mapping
Proof: First, we construct a desired mapping Let v
0
∈ V
be a fixed element. For any x
∈
I
R
1
and y ∈
E
R
1
,
if there exist relations
r
x
, r
y
∈ R
such that
and
(9.196)
then define
G
1
(
x,y) = G
(
h
(
x
),h
(
y
))
(9.197)
If either
r
x
or
r
y
or both do not exist, we define
G
1
(x,y) = v
0
(9.198)
defined by C
v
(
u
) = cg
(
u
)

General Systems: A Multirelation Approach
241
It can be shown that
is well defined.
Second, we show that
S
1
is generally controllable on V' relative to
Suppose that for each v
∈ V' there exist sets W
v
and M
v
⊂ M and a
mapping C
v
: W
v
→ p
(
I
R(
M
v
))
such that, for each u ∈ W
v
, there exists a
y
u
∈
E
R
such that G
(
z,y
u
) =
v
for some
z
∈
C
v
(
u
). We now let
h
–1
(
M
v
)
⊂
M
1
and define
a control function
as follows: For each
u
∈
W
v
,
(9.199)
Now it only remains to show that ¹C
v
is a control function of S
1
. In fact, for each
u
∈
W
there exists
y
∈
E
vu
R such that
G(z,y ) = v for some z
∈ C
v
(
u
)
(9.200)
u
so there exists
such that
where
Therefore, S
1
is generally controllable on
V'
relative
to G
1
.
Theorem 9.6.6. Let {
S
i
: i ∈ I} be a set of systems, where I is an index set, such
that there exists an i
0
∈ I such that the system S
i
0
is generally controllable on V'
relative to a mapping
Then the Cartesian product system
Π
cp
{S
i
: i ∈ I
}
is also generally controllable on V' (relative to a different mapping
where it is assumed that
(M,R).
The proof follows from Theorems 9.3.10 and 9.6.5.
Theorem 9.6.7. Suppose that h : S = (M, R) → S
1
= (
M
1
,R
1
) is an embedding
mapping from a system S into a system S
1
such that S is generally controllable on
V’ relative to a mapping G :
I
R ×
E
R → V. Then, S
1
is generally controllable on
V’ relative to a mapping G
1
:
I
R
1
×
E
R
1
→
V.
Proof:
We first construct a desired mapping
Let v
0
∈
V
be a fixed element. For any
x
∈
I
R
1
and y ∈
E
R
1
, if there exist
x
*
∈
I
R and y
*
∈
E
R
such that h
(
x
*
) = x and h
(
y
*
) = y, we define
G
1
(x,y) = G (x
*
,y
*
)
(9.201)

242
Chapter 9
From the hypothesis that h is 1–1, we see that Eq. (9.201) is well-defined, for the
existence of x
*
and y* is unique. If one or both of the elements x
*
and y
*
do not
exist, then we define
G
(
x,y
) =
v
(9.202)
10
We then have defined a mapping
Second, we show that the system S
1
is generally controllable on V' relative to
the mapping G
1
. Suppose that for each v ∈ V' there exist sets W
v
and M
v
⊂
M
and a mapping
such that, for each u
∈ W
v
, there exists a
y
E
u
∈
R such that G
(
z,y
u
) = v for some z ∈ C
v
(
u
). We now let h
(
M
v
) ⊂ M
1
and
define a control function
as follows: For each
u
∈
W
v
,
(9.203)
It remains to show that ¹
1
C
v
is indeed a control function for S
1
. For each u ∈ W
v
there exists a y
E
u
∈
R
such that
G
(
z,y
u
) = v for some z ∈ C
v (u
)
(9.204)
Therefore,
(9.205)
where
and
Corollary 9.6.1. If a subsystem A =
(
M
A
, R
A
)
of a system S = (
M, R
)
is generally
controllable on V’ relative to a mapping
then S is generally
controllable on V' relative to a mapping
Theorem 9.6.8.
Let
{
S
i
= (M
i
, R
i
) : i ∈ I
}
be a set of systems and
{
V
i
⊂ V
:
i
∈
I
}
a set of nonempty subsets of V. If each system Si is generally controllable on the
is generally controllable on
∪
subset V
i
relative to a mapping
then ⊕
{
S
i
: i ∈ I} = (M,R
)
{
V
i
:
i
∈
I
}
relative to a mapping
where for each i ∈ I and any
Proof: From the definition of free sums of systems, it follows that
(9.206)
where
for any distinct i,j ∈ I. Let G be an extension of
the mappings {
G
i
: i ∈ I}; i.e., G is a mapping from
I
R ×
E
R into V such that for
any
then G
(
x,y) = G
i
(
x,y
).

General Systems: A Multirelation Approach
243
To show that the free sum
⊕
{
S
i
: i ∈ I
}
is generally controllable on
∪
{V
i
:
i
∈
I
}
relative to G, we pick an arbitrary v
∈
∪
{
V
i
: i ∈ I}. Then there exists an i ∈ I
such that
v
∈
V
i
. Therefore, there exist sets W
v
and M
v
⊂
M
i
⊂
∪
{
M
j
: j ∈ I
} and
a mapping
(9.207)
such that for each
u
∈
W
v
, there exists a y
u
∈
E
R
i
⊂
E
R
such that
G(z,y
u
) = v for some z ∈ C
v
(u
)
(9.208)
This proves the theorem.
In the following, we conclude this section with a discussion of controllabilities
of time systems.
Theorem 9.6.9. Suppose that {S, l
ts
,
T
}
is a linked time system. If there exists a
t
∈ T such that
(a) S
t
is a nondiscrete input–output system,
(b)
for each s
<
t,
(c)
for each s
>
t,
then each state S
s
of the linked time system has a nondiscrete partial system which
is an input–output system.
Proof: Let S
t
=(M
t
, R
t
) and
X
t
and
Y
t
be input and output spaces of the state
S
t
, respectively. If s < t, let be a partial system of the system S
s
defined by
Then
is a nondiscrete input–
output system with input space
l
st
(X
t
) and output space l
st
(Y
t
). Finally, if s > t,
let be a partial system of
S
s
defined by
R
s
: l
ts
(
r
) ∈ R
t
}. Then
is a nondiscrete input–output system with input space
X
s
= {x ∈ M
s
: l
ts
(x
)
∈
X
t
} and output space
Y
s
= {y ∈ M
s
: l
ts
(
y
)
∈
Y
t
}.
Theorem 9.6.10.
Suppose that
{
S, l
ts
, T} is a linked time system such that
(a) T has an initial element t
0
.
(b) Each l
t
0
s
is surjective with
l
t
0
s
(
R
s
)
∩
R
t
0
≠
Ø.
(c) S
t
0
is a nondiscrete input–output system with input space X
t
0
and output
space Y
t
.
0
(d) S
t
0
is v-controllable relative to a mapping G
: Dom(
X
t
0
)
×
Ran(
Y
t
0
)
→
V.
