Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

264

Chapter 10

The proofs that (3) implies (1) and (2) implies (3) are clear because we can

define the desired mappings R

and R

and

where 0

and 0

are the additive identities in the linear spaces

and

, respectively.

Proof that (1) implies (2). Suppose S is a linear system and 0

and 0

are the

additive identities in X and Y

, respectively. Define

(10.20)

Then C

≠ ø; in fact, 0

∈ C because , and C is a linear subspace

over

. Consider the quotient space with addition +*

and scalar multiplication ·* defined by

and

for any

α ∈

and any (

+ C ) and

Define a mapping by letting

(10.21)

if (x

)

∈

for every

∈

(

S). Then σ is well defined. In fact, for each x ∈ D(S

)

and any

∈

satisfying

and thus , so . This means that

Define a linear mapping

as follows:

(10.22)

We now choose an isomorphism

C ⊕ C → Y satisfying I

(

) = y for every

∈ Y

Now the desired mapping

(

)

→

can be defined by

Then (x,y ) ∈ S if and only if there exists c ∈ C such that ρ

(

x) = y. In fact, if

(

x, y

)

∈

, there exists

∈

such that

, so

On the other hand, if (

y) ∈ X × Y is such that there exists c ∈ C with ρ (

x )=y

then

, so

. Suppose

Then y = y

for some

∈ C; hence,

(10.23)

This completes the proof of the theorem.

Example 10.2.1. Three examples are given to show that the concept of linear

systems is an abstraction of different mathematical structures.

(a) Suppose S is a system described by the following linear equations:

Systems of Single Relations

265

where x

, i = 1,2, . . .

, are n variables, m is the number of equations, a

, (i =

1,2

, . . . ,

;

= 1,2, . . .

) are the coefficients of the system, and

j = 1,2,. . . , m,

are the constraints of the system. The system S can then be rewritten as a linear

system (

M, {

}), where the object set M is the set of all real numbers, and

where

is fixed such that for

each i = 1, 2, … , m.

(b) Suppose a given system S is described by the differential equations

where

, and f (t

)

are continuous functions defined on the

interval [

, b]. The system S can be rewritten as a linear system (M, {

}) in the

following way: The object set M is the set of all continuous functions defined on

[

, b], and the relation r is defined by

where y

∈ M is a fixed function such that

a system such that the object set M is a linear space over

system if for each relation r

∈ R there exists an ordinal number n = n(r) such

. Then S is a linear

transformations on X. Then Y can be studied as a linear system (X

R), where,

for each relation r

∈ R, there exists a transformation y ∈ Y such that for any

if and only if y(

) = x

In Example 10.2.1(b), S is not an input–output linear system. Generally, the

concept of general linear systems is the following: Let

be a field and S = (M

)

that r is a linear subspace of M

We will study only input–output linear systems

defined in the beginning of this section.

An input–output system S

⊂ X × Y is a functional system if S is a function

from the input space X into the output space Y. Let S

⊂ X × Y and S

: Y → X

be a linear system and a linear functional system, respectively. Then the feedback

system of S by S

is defined as the input–output system S

′

such that

and

(10.24)

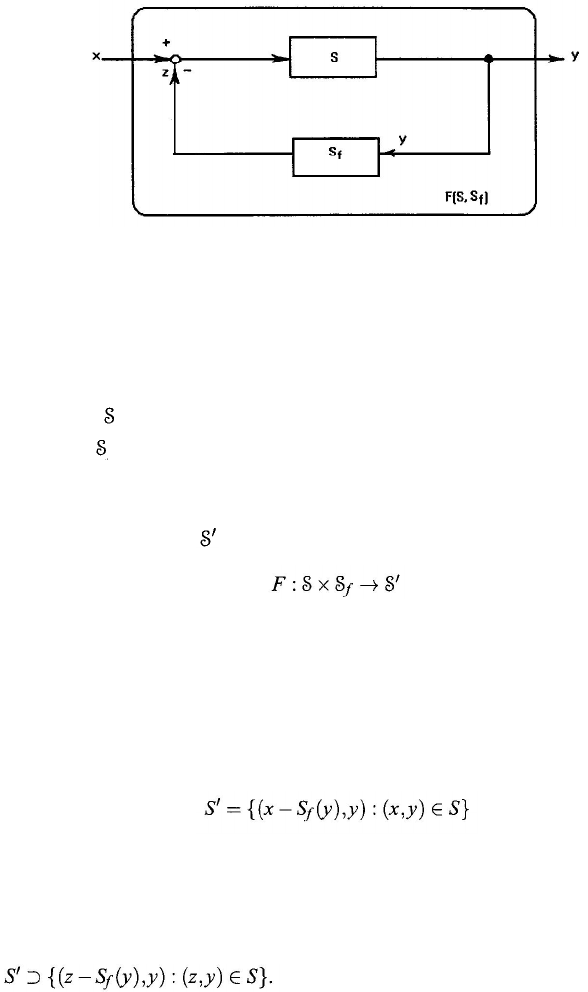
266

Chapter 10

Figure 10.4. Structure of feedback systems.

The systems S and S

are called an original system and a feedback component

system, respectively.

Let

= {

S ⊂ X × Y : S is a linear system}

(10.25)

= {S

: Y → X : S

is a linear functional system}

(10.26)

and

= {S'

⊂ X × Y : S' is a subset}

(10.27)

Then a feedback transformation is defined by Eq. (10.24), which

is called the feedback transformation over the linear spaces X and Y. Figure 10.4

shows the geometric meaning of the concept of feedback systems.

The following theorem gives a concrete structure of each feedback system.

Theorem 10.2.2. Suppose that S

⊂ X × Y is a linear system and S

: Y → X a

linear functional system. Then a subset S'

⊂ X × Y is the feedback system of S by

, iff

(10.28)

Proof: Necessity. Suppose S' is the feedback system of S by S

. Then,

by the definition of feedback systems, for each (

x, y) ∈ S', (x + S

(y), y) ∈ S.

This implies that (x ,

)

∈

{ (

z – S

(y), y) : (z, y

)

∈

}. Again, the relation in

Eq. (10.24) implies that for each element (

x, y) ∈ S

, (

x – S

(y), y) ∈ S'. That is,

Sufficiency. Clear because Eq. (10.28) implies the relation in Eq. (10.24).



Systems of Single Relations

267

Theorem 10.2.3. Suppose that S, S' ⊂ X × Y are linear systems and S

→

is a linear functional system such that

(10.29)

Then F

(

–S

) = S, where –S

: Y → X is the linear functional system defined

(10.30)

for every y

∈ Y.

The proof is straightforward and omitted.

Theorem 10.2.4.

For each linear system S

⊂

Y, there exists a linear functional

system S

: Y → X such that F(

S,S

) = S, that is, S is a feedback system of itself.

Proof: The desired linear functional system S

: Y → X can be defined by

(10.31)

for every y

∈ Y. Then, Eq. (10.28) says that S = F(

S,S



Theorem 10.2.5 discusses the control problem: A linear structure (say, system)

S ⊂ X × Y is fixed. According to some predefined targets, we need to produce a

new linear structure (say, a linear subspace) S'

⊂ X × Y

. Can we design a feedback

process

: Y → X such that F (

S, S

)

= S'

Theorem 10.2.5. Assume the axiom of choice. For each linear system S ⊂ X × Y

and arbitrary linear subspace S'

⊂ X × Y, there exists a linear functional system

: Y → X such that F(

S,S

) = S' iff R

(

) = R

(

) and N

(

) = N

(

), where

(

) indicates the null space of the input–output system W ⊂ X × Y, defined by

(10.32)

Proof:

Necessity. Suppose there exists a linear functional system

: Y → X

such that F

(

S,S

) = S'. Then Theorem 10.2.2 implies that R(

S')

= R

(

) and that

268

Chapter 10

Sufficiency. Suppose that S and S' have the same output space and the null

space; i.e., R(

) = R

(

) and N

(

) = N(

). We define a linear functional system

: Y → X such that F(

S,S

) = S'.

For each element y

∈ R (

), let

(10.33)

and

(10.34)

From the Axiom of Choice, it follows that there exist mappings

(10.35)

and

(10.36)

such that

[

i.e.,

(

y) ∈ S].

and

[i.e.,

We are now ready to check that for each y ∈ R (

) = R

(

)

(10.37)

Thus, the mappings C and C' are well defined.

Let {

: i ∈ I

} be a basis in the linear space

(

)

, where I is a finite or infinite

index set. We now define a linear functional system

(10.38)

satisfying

, for each i ∈ I. Then we make the following

claim.

Claim. The systems S, S', and S

have the property that F

(

S, S

)= S'.

In fact, for each element (

x,y

) ∈ S', for an i ∈ I, we have

since

(10.39)

Therefore, from Eq. (10.39),

(10.40)

Systems of Single Relations

269

Now let (x

) ∈ S we then have

, because

(10.41)

Hence, we have from Eq. (10.41) the opposite implication of Eq. (10.40). That is,

for every i

∈ I,

(10.42)

It now remains to show that for each pair (x

y) ∈ X × Y, the relation in

Eq. (10.24) holds. Let (

y) be an arbitrary element in S'. Then

for a

finite number of

’s from the basis {

: i ∈ I

}, where each

is a nonzero number.

Then

In fact,

(10.43)

This gives us the implication from the right to left in Eq. (10.24). The opposite

implication can be shown as follows. For each pair

In fact, let

for some finite number of nonzero coefficients

, where

each y

is from the basis {

: i ∈ I

}. Then

(10.44)

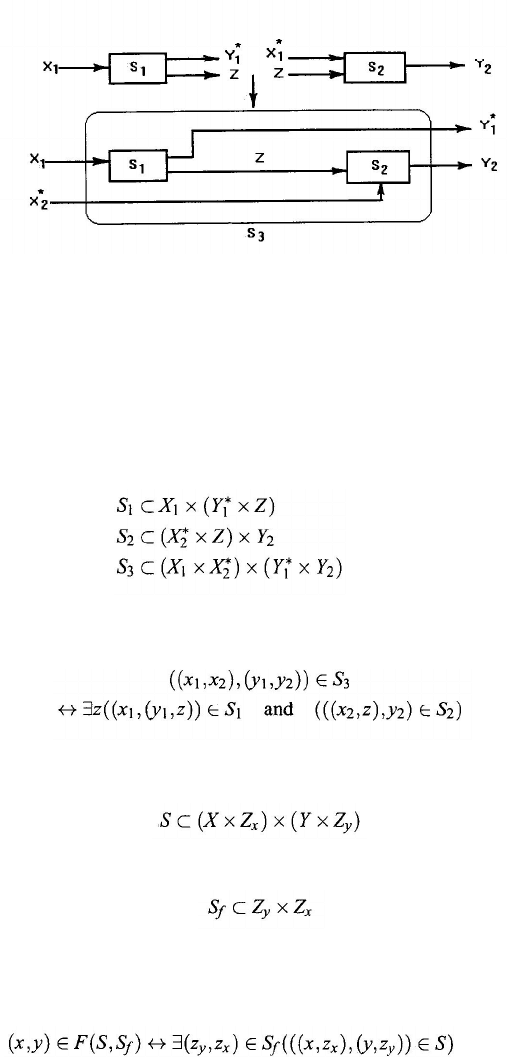
270

Chapter 10

Figure 10.5. Structure of cascade connections of systems.

This completes the proof of Theorem 10.2.5.



We conclude this section with a discussion of a more general definition of the

concept of feedback systems. Let

be a system connecting operator, termed the

cascade (connecting) operation. The operation

is defined as follows: Let S

1,2,3, be input–output systems such that

(10.45)

(10.46)

(10.47)

where it is assumed that no algebraic properties are given on each set involved.

The three systems satisfy

= S

if and only if

(10.48)

Figure 10.5 shows the geometric meaning of the cascade connection of systems.

We now let S and S

be two input–output systems such that

(10.49)

and

(10.50)

where

is called a feedback component of S. The relationship between the two

systems is displayed in Fig. 10.6.

The feedback system F

(

S,S

) of S by S

is defined by

(10.51)

Systems of Single Relations

271

Figure 10.6. Construction of general feedback systems.

In constructing F

(

S, S

) step by step, we first cascade S and S

(i.e., find S

)

and then input one of the two outputs of the system S

Without special explanation in this book, by feedback system we always mean

the definition given by Eq. (10.24).

10.3. Feedback-Invariant Properties

Some properties of original systems may be kept by their feedback systems

and some may not. Those properties of original systems invariant under the

feedback transformation F are of special interest in research on feedback systems.

Feedback invariance has played a crucial role in characterizing homeostatic or

explosive system behaviors in various areas such as biology, engineering, social

science, and so on.

A property of a linear system S

⊂ X × Y is called feedback invariant with

respect to

if the property also holds for the feedback system F

(

S, S

) for each

linear functional system S

∈

Corollary 10.3.1. Let S

⊂ X × Y and S

: Y → X be a linear system and a linear

functional system, respectively. Then the feedback system F

(

S, S

) is a linear

system over X

× Y and R

(

S, S

)) = R

(

S) and N

(

S, S

)) = N

(

Proof: The linearity of the feedback system F

(

S, S

) follows from Theorem

10.2.2. The equations R

(

(S, S

)) = R

(

S) and N

(

S, S

)) = N

(

S) come from

Theorem 10.2.5 here the Axiom of Choice is not used.



272

Chapter 10

Theorem 10.3.1. Let S : X → Y and S

: Y → X be linear functional systems such

that S is surjective. Then D

(

S, S

)) = D(S) iff(

–

) : Y → Y is surjective,

where I : Y

→ Y indicates the identity mapping; i.e., I

(

y) = y for each y ∈ Y.

Proof: Sufficiency. It is clear that D

(

(S, S

)) ⊂ D

(

S). Let x ∈ D

(

S) be

arbitrary. There then exists some y

∈ Y such that (x, y) ∈ S. Since (I – S

) :

→ Y is surjective, there exists exactly one ∈ Y such that

(10.52)

This implies that

(10.53)

That is, ∈ S. Hence, x ∈ D

(

S, S

)).

Necessity. Pick an arbitrary y

∈ Y. From the hypothesis that S is a surjec-

tive system, it follows that there exists some x

∈ X such that S

(

x) = y. Since

(

S, S

)) = D

(

S), for this x there exists some

∈

such that (

)

∈

(

S, S

);

i.e.,

∈ S. Hence,

(10.54)

Thus

, i.e., This proves that (

I – S

) :

→

is surjective.



Theorem 10.3.2. Let S ⊂ X × Y be a linear system and S

: Y → X a linear

functional system. Then D

(

S, S

)) = X iff for each x ∈ X there exists a y ∈ R(S

)

such that

(

x + S

(

y), y

)

∈

The proof is clear from Eq. (10.24).

Theorem 10.3.3. Let S : X → Y be a linear functional system. Then for each

arbitrarily fixed S

∈

, the feedback system F

(

S, S

) is injective iff the original

system S is injective.

Proof: Sufficiency. Suppose the original system S is injective, and let S

∈

be arbitrary. Suppose the feedback system F

(

S, S

) is not injective. Thus, there

exist distinct x

∈ D

(

S, S

)) such that

(10.55)

Systems of Single Relations

273

for some y ∈ R

(

S). By Eq. (10.24), we have (x

+ S

(

)

), (

(

)

∈

Therefore, from the hypothesis that the system S : X → Y is injective, it follows

that

+ S

(

y) = x

+ S

(

y); i.e., x

= x

, contradiction.

Necessity. Suppose

(

S, S

) is injective. From Theorem 10.2.3,

(

(S, S

), –S

) = S

Applying the proof for sufficiency, we know that

is injective.



Combining what have been obtained in this section, the following theorem is

evident.

Theorem 10.3.4. Range space, null space, linearity, injectivity, surjectivity, and

bijectivity of original systems are feedback invariant with respect to

In the rest of this section, we study feedback-invariant properties of MT-time

systems. Let T be the time axis defined as the positive half of the real number

line; i.e., T =

[0, +

∞

). Let A and B be two linear spaces over the same field .

We define

= {

x : x is a mapping T → A

}

(10.56)

and

= {

x : x is a mapping T → B

}

(10.57)

Then the sets A

and B

can be made linear spaces over as follows: For any

elements

ƒ, g

∈

(respectively,

∈

), and α ∈

(ƒ + g

)(

) = ƒ

(

t) + g(t

)

(10.58)

and

(

αƒ

)(

) =

· ƒ

(

)

(10.59)

for each t ∈ T.

Assume the input space X and the output space Y in the preceding discussion

are linear subspaces of A

and B

, respectively; i.e., X ⊂ A

and Y ⊂ B

Proposition 10.3.1. For any linear system S

⊂ X × Y and any linear functional

system S

: Y → X, the feedback system F

(

S, S

) is a linear system over A

× B

The proof is straightforward and is omitted.

Each input–output system S

⊂ A

× B

is termed an MT-time system,

(Mesarovic–Takahara time system). Therefore, Proposition 10.3.1 implies that

the feedback transformation defined in Section 10.2 is well defined on the class of

all MT-time systems.