Яновский Б.М. Земной Магнетизм. Том 2

Подождите немного. Документ загружается.

Влияние вариаций

221

дуктивного происхождения, и вместе с тем определить величину

магнитной восприимчивости породы в целом.

Так как наибольшее значение аномальное поле принимает

в центре аномалии, то влияние вариаций должно сказываться

наибольшим образом над центром ее. Поэтому рассмотрим, ка-

ковы должны быть вариации магнитного поля над центром

аномалии, предполагая что порода намагничена вертикально

= 0).

При χ = О

(7.4)

где А — коэффициент пропорциональности, зависящий от гео-

метрических параметров породы и расстояния ее до поверхно-

сти Земли. Следовательно, вариации аномального поля будут:

(7.5)

Так как

где /

— остаточная намагниченность, κ — магнитная восприим-

чивость породы и Ζ

— вертикальная составляющая нормаль-

ного поля, то

Наблюдаемая же вариация будет суммой нормальной вариа-

ции bZ

и аномальной οΖ

, т. е.

(7.6)

Следовательно, вариации вертикальной составляющей над

центром аномалии должны быть пропорциональны нормальной

вариации, при этом коэффициент пропорциональности, как по-

казывает уравнение

(7.6),

всегда больше единицы, и поэтому

Если остаточная намагниченность невелика и ею можно

пренебречь, то

(7.7)

Если же, наоборот, считать индуктивную намагниченность ма-

лой по сравнению с остаточной /

, то

(7.8)

222

Использование магнитных вариации

[гл.

VII

Наконец, если восприимчивость породы очень мала

и ею

можно пренебречь,

то при

любом значении остаточной намагни-

ченности

(7.9)

т.

е.

постоянная намагниченность породы

не

изменяет вариаций

нормального поля.

Если

и κΖ

имеют одинаковый порядок,

и ни

одной

из

этих величин невозможно пренебречь,

то

уравнение позволяет

определить отношение остаточной намагниченности породы

ее индуктивной намагниченности.

Заменяя

уравнении

= Ζ — Ζ

решая

его

относительно

получим

(7.10)

Таким образом, зная

К и N из

наблю-

дений, можно определить

из

уравнений

(7.6), (7.8) и

(7.10)

следует,

что

(7.11)

т. е.

наблюдения вариаций позволяют опре-

делить

не

только

Q, но и

магнитную восприимчивость

κ и

оста-

точную намагниченность

если известен коэффициент

А.

Коэффициент

находится

по

одной

из

формул, данных

3, гл. V,

если

свою очередь известна форма залегающей

породы.

Рассмотрим, какова точность определения

κ, J

и Q по на-

блюдениям вариаций вертикальной составляющей. Дифферен-

цируя уравнения

(7.10), (7.11),

будем иметь

(7.12)

где

Как видно,

при N « 1, т. е.

когда индуктивная намагничен-

ность мала, определение

κ и Q

становится невозможным,

так

как погрешность

этом случае может достигать значения,

в не-

где

Влияние вариаций

223

сколько раз большего самой величины. Точно так же при К ^ N,

т. е. когда остаточная намагниченность невелика, определение

/„ делается также невозможным.

Формулы показывают, что погрешность в определении всех

величин в сильной степени зависит от величины погрешности

измерения вариаций, а для определения /

и κ — и от погреш-

ности определения коэффициента А.

В Курской аномалии на участке, где проводились наблюде-

Ζ,

ния автором в 1936 г., отношение —=^ в некоторых точках дохо-

ди

дит до четырех, и Ζ

принимает значение Ζ

= 1,5 э, тогда как

нормальная величина Ζ

= 0,4 э.

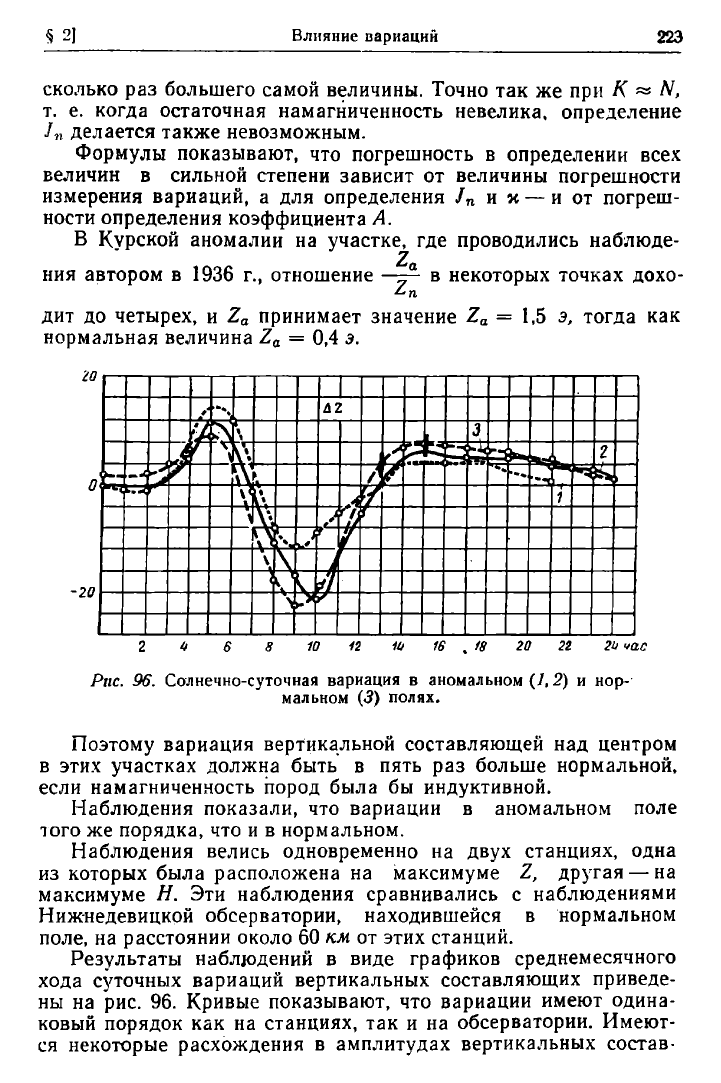
Рис. 96. Солнечно-суточная вариация в аномальном (/, 2) и нор-

мальном (<?) полях.

Поэтому вариация вертикальной составляющей над центром

в этих участках должна быть в пять раз больше нормальной,

если намагниченность пород была бы индуктивной.

Наблюдения показали, что вариации в аномальном поле

того же порядка, что и в нормальном.

Наблюдения велись одновременно на двух станциях, одна

из которых была расположена на максимуме Ζ, другая — на

максимуме Н. Эти наблюдения сравнивались с наблюдениями

Нижнедевицкой обсерватории, находившейся в нормальном

поле, на расстоянии около 60 км от этих станций.

Результаты наблюдений в виде графиков среднемесячного

хода суточных вариаций вертикальных составляющих приведе-

ны на рис. 96. Кривые показывают, что вариации имеют одина-

ковый порядок как на станциях, так и на обсерватории. Имеют-

ся некоторые расхождения в амплитудах вертикальных состав-

224

Использование магнитных вариаций

[гл.

VII

ляющих, фазы

же у

всех компонент одинаковы. Однако

эти

расхождения можно отнести больше

погрешностям самих

измерений,

чем к

влиянию вариаций

на

изменение намагничен-

ности пород. Таким образом,

эти

наблюдения показали,

что

аномальное поле исследованного участка вызвано

большей

своей части остаточной,

а не

индуктивной намагниченностью

пород. Лабораторные исследования

[51]

пород Курской анома-

лии показали,

что они

имеют остаточную намагниченность,

в не-

сколько

раз

большую,

по

сравнению

индуктивной,

что

также

доказывает «остаточный» характер происхождения Курской

аномалии.

Наблюдения вариаций

на

Курской магнитной аномалии

были повторены

более чувствительной аппаратурой

в 1960 г.

кафедрой физики земной коры

ЛГУ и

Институтом физики

Земли

АН

СССР

[34].

Участок аномалии,

где

производились наблюдения, имел

максимальное значение вертикальной составляющей

0,242

э.

т.

е.

почти

шесть

раз

меньше,

чем на

участке наблюдений

1936 г.

Однако благодаря более высокой чувствительности аппа-

ратуры

эти

наблюдения позволили

не

только установить оста-

точный характер намагниченности пород, вызывающих анома-

лию,

но и

сделать оценку величины индуктивной намагниченно-

сти.

По

формулам

(7.10) и (7.11)

была определена магнитная

восприимчивость

κ,

индуктивная намагниченность

- и

отноше-

ние

которые оказались равными:

κ=0,08;

Q=l,2;

/г = 0,36.

Хотя погрешность этих определений была

не

меньше

20—

30%, тем не

менее

эти

наблюдения доказали практическую воз-

можность применения метода естественных магнитных вариа-

ций

для

исследования магнитных свойств горных пород

в их

естественном залегании.

Для

повышения

же

точности определе-

ния необходима лишь более высокочувствительная аппаратура.

Часть II. ГЕОМАГНИТНЫЕ ИЗМЕРЕНИЯ

ГЛАВА

VIII

РАСЧЕТ МАГНИТНОГО ПОЛЯ КАТУШЕК, ПРИМЕНЯЕМЫХ

В МАГНИТОМЕТРИИ

Во многих вопросах исследования магнитных свойств гор

них пород, а также в вопросах геомагнитных измерений сущест-

венную роль играют катушки с обмотками из провода, по кото-

рому протекает ток. Форма и размер этих катушек зависят от

тех требований, которые к ним предъявляют. Однако общим

требованием к любой из форм катушек является однородность

создаваемого ими магнитного поля в заданном объеме про-

странства. Требованием же частного характера может служить

доступность для наблюдателя того объема, в котором магнит-

ное поле однородно.

Чтобы удовлетворить этим требованиям при выборе разме-

ров и формы катушки, а также при расчетах создаваемого ими

магнитного поля Н, необходимо знать аналитическую зависи-

мость напряженности поля H от параметров катушки и коорди-

нат точек пространства.

Поэтому, прежде чем приступить к рассмотрению методов

геомагнитных измерений и исследований, необходимо рассмо-

треть вопросы теоретического расчета таких катушек.

Практически все катушки представляют собой совокупность

ряда плоских контуров, расположенных параллельно друг

другу. Поэтому расчет магнитного поля для них сводится к на-

хождению потенциала одного из контуров и последующему

суммированию или интегрированию. В магнитометрических ис-

следованиях имеют применение катушки в форме: соленоидов,

колец Гельмгольца, квадратных катушек, катушек Фанзелау.

Рассмотрению поля этих катушек и посвящены следующие па-

раграфы.

15 В- М. Яновский

226

Расчет магнитного поля катушек

1гл.

VIII

§ 1. Магнитное поле линейного контура

Рис. 97. К выводу поля линейного

кругового тока.

Магнитный потенциал U плоского линейного контура, по

которому протекает ток, выражается как произведение с обрат

ным знаком силы тока I на телесный угол Ω, под которым виден

контур из данной точки Р, т. е.

(8.1

Поэтому задача нахождения магнитного поля кругового кон-

тура должна заключаться в отыскании Ω как функции коорди

нат точки Р, при заданном радиусе контура R.

Положим, что имеется кру-

говой контур С (рис. 97), рас-

положенный своей плоскостью

перпендикулярно к плоскости

чертежа. Примем за ось *-ов

ось кругового контура 0\Х, по-

ложив начало координат в лю-

бой точке О на этой оси. Тогда

полярными координатами точ-

ки Ρ будут: расстояние ОР=т

и угол POx =

В силу симметрии магнит-

ного поля относительно оси Ох магнитный потенциал U точки

Ρ будет зависеть только лишь от угла θ и полярного расстояния

г точки Ρ от начала координат О, т. е.

Из теории шаровых функций известно, что всякая функция

от координат гиб может быть разложена в ряд по степеням

полярного расстояния г по одной из следующих формул:

(8.2)

где Р

(cos6)—полиномы Лежандра; А

и В

—по-

стоянные коэффициенты, не зависящие от координат точки Р.

Полиномы Лежандра представляют собой алгебраические

функции от

cos9

степени η и являются коэффициентами при α

в разложении в ряд по биному Ньютона выражения

(8.3)

Первые четыре полинома имеют следующий вид:

Магнитное поле линейного контура

227

(8.4)

Из всех свойств, которыми обладают полиномы Лежандра,

укажем

на

следующие, необходимые

для

дальнейших выводов:

Если аргумент полинома

cos6

меняет знак,

то

полиномы

четных степеней остаются

без

изменения,

полиномы нечетных

степеней меняют свой знак.

2: Производная полинома Лежандра

по cos6

выражается

формулой:

(S.3)

чем

можно убедиться непосредственно, продифференцирован

выражения

(8.4).

3. При cos6 = 1 все

полиномы обращаются

единицу,

т. е.

(\)

= 1.

При cos9 = 0

нечетные полиномы обращаются

нуль,

а четные

(8.6)

После этих замечаний переходим

выводу выражения

те-

лесного угла

Ω, т. е. к

нахождению коэффициентов

и В

уравнениях

(8.2).

Чтобы найти коэффициенты

и В

достаточно иметь .раз-

ложение

Ω для

какого-либо частного случая

сравнить коэффи-

циенты этого разложения

коэффициентами

и В

при

оди-

наковых степенях

или ^

η+ι

Если взять точку

Р\ на оси ко-

ординат,

то

телесный угол Ωρ,,

под

которым

из нее

виден круго-

вой контур, легко находится.

Действительно, описав

из

точки

шаровую поверхность

радиусом

PiC = ρ,

будем иметь

(8.7)

где

— угол OPiC,

a cos {η, ρ)

имеет значение

или +1 или

—1,

β зависимости

от

направления тока

контуре. Положим,

что

ток направлен

по

часовой стрелке", если смотреть

на

него

из на-

чала координат, тогда

cos

(η,

ρ) = 1, а

228 Расчет магнитного поля- катушек

[гл.

vin

(8.8)

где ψ = <0{ОС (см. ,рис. 96), а ро — расстояние от начала ко-

ординат до точки контура (ро = ОС). Полагая г <р

и вынося

за знак радикала, будем иметь

(8.9)

Выражение, стоящее в квадратных скобках, можно предста

вить в виде ряда, расположенного по полиномам Лежандра,

тогда

Подставляя это значение cos α в выражение (8.7) для Qv

после простых преобразований получим

так как

Выражение, стоящее иод знаком суммы в квадратных скоб

ках, по свойству полинома Лежандра, можно заменить согласно

формуле (8.5)' через производную от полинома. 'Поэтому

(8.10)

Для точек, находящихся, на оси контура, 0 = 0, поэтому вы

ражения телесного угла

(8.2')

обратятся в одно из следующих.

Магнитное поле линейного контура

229

Сравнивая первое

из них с

выражением

(8.10),

находим

Следовательно, потенциал кругового контура

любой точке

л;

пространства

при

условии,

что

г<р

θ<2» выразится:

(8.11)

Для точек, лежащих слева

от

начала координат,

для

которых

, выражение

для

потенциала будет иметь

вид:

(8.12)

гак

как

проекция точки

Ρ на ось л:-ов

будет лежать слева

от на-

чала координат. Составляющие напряженности магнитного

поля

по оси χ и по оси у

определяются

из

соотношений:

Подставляя

в эти

выражения значение

U из

уравнения

(8.11),

получим:

Î8.13)

230

Расчет магнитного поля катушек

[гл.

VIII

где

Рп

(cos9)

и Р

' (cos ψ)

обозначают производные

по cos θ

cos ψ.

Далее, заменяя

уравнении

(8.12)

выражение, стоящее

квадратных скобках,

по

формуле

(8.5) и

принимая

во

внима-

ние,

что P

'[cos(jt — ψ)]=

(—

n_1

/V(

cos

ty).

получим

для

следующее выражение:

(8.14)

Принимая

во

внимание формулы

для

полиномов Лежандра

и заменяя

sin ψ и cos ψ их

значениями через

Хо

= ОС и ро, по-

лучим,

точностью

до

членов четвертого порядка

Для точек, лежащих

на оси у, у

которых

θ = 90° и г = у.

формулы

для Н

и Η

примут

вид:

(8.15)

(8.16)