Яновский Б.М. Земной Магнетизм. Том 2

Подождите немного. Документ загружается.

§ 3]

Методы расчета прои.чиодных

161

Формулами преобразования служат обычные формулы пере

хода одной системы координат в другую:

(6.1)

где

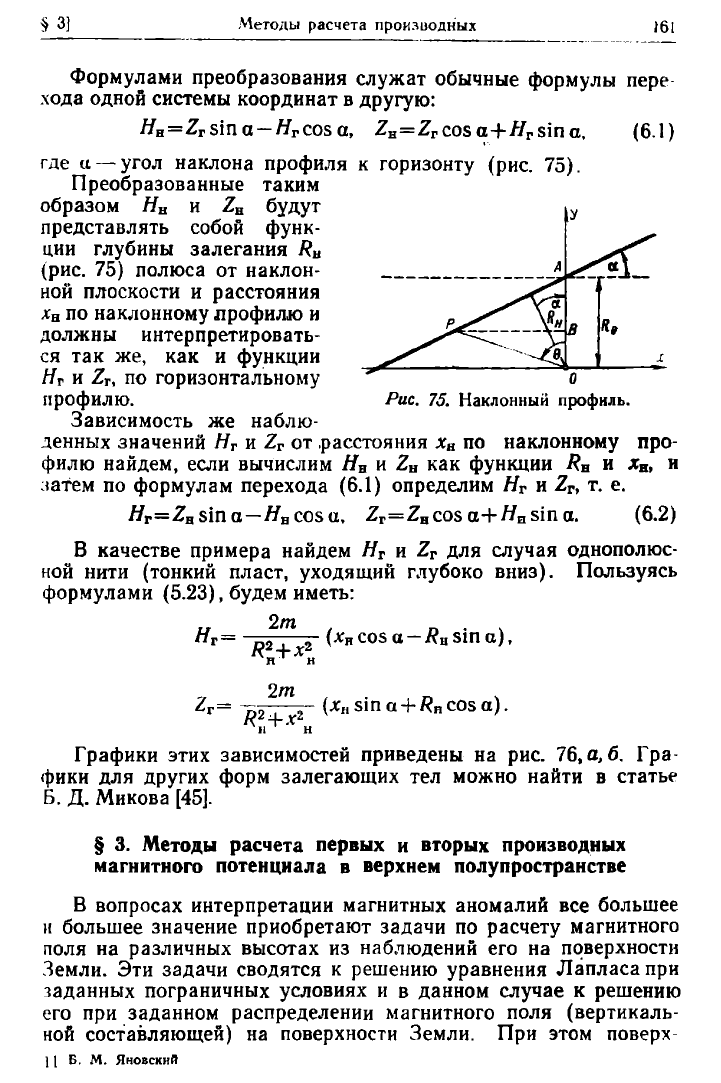
и — угол наклона профиля к горизонту (рис. 75)

Преобразованные таким

образом Я

и Z

будут

представлять собой функ-

ции глубины залегания R

(рис.

75) полюса от наклон-

ной плоскости и расстояния

по наклонному профилю и

должны интерпретировать-

ся так же, как и функции

и Ζ

, по горизонтальному

профилю.

Зависимость же наблю-

Рис. 75. Наклонный профиль.

денных значений Я

и Ζ

от .расстояния х

по наклонному про-

филю найдем, если вычислим Я

и Ζ

как функции R

и х

, и

затем по формулам перехода (6.1) определим Я

и Ζ

, т. е.

(6.2)

В качестве примера найдем Я

и Ζ

для случая однополюс-

ной нити (тонкий пласт, уходящий глубоко вниз). Пользуясь

формулами

(5.23),

будем иметь:

Графики этих зависимостей приведены на рис. 76,а, б. Гра-

фики для других форм залегающих тел можно найти в статье

Б.

Д. Микова [45].

§ 3. Методы расчета первых и вторых производных

магнитного потенциала в верхнем полупространстве

В вопросах интерпретации магнитных аномалий все большее

и большее значение приобретают задачи по расчету магнитного

поля на различных высотах из наблюдений его на поверхности

Земли. Эти задачи сводятся к решению уравнения Лапласа при

заданных пограничных условиях и в данном случае к решению

его при заданном распределении магнитного поля (вертикаль-

ной составляющей) на поверхности Земли. При этом поверх

] I Б. М. Яновский

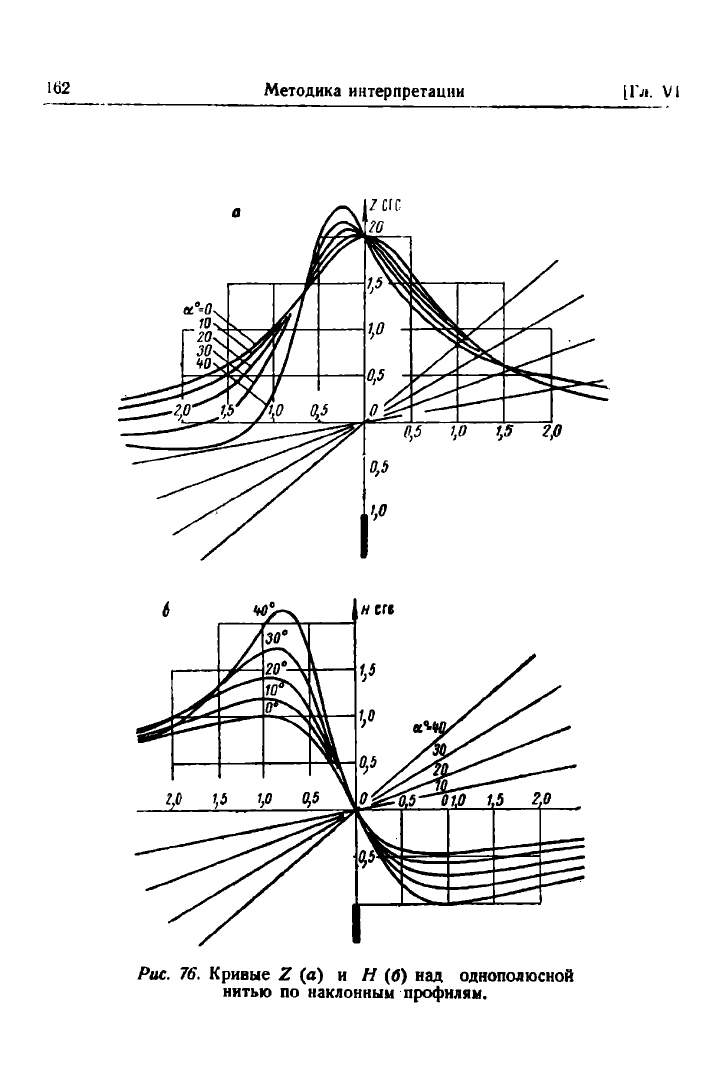
Рис. 76. Кривые Ζ (α) и Η (б) над однополюсной

нитью по наклонным профилям.

Методика интерпретации

Методы расчета производных

163

ность Земли, ввиду ограниченного размера аномалий, принято

считать плоской.

Общее решение задачи для плоской поверхности дается в кур-

се теории потенциала и носит название проблемы Дирихле и

Неймана.

Для случая плоского распределения поля потенциал U

любой точке пространства Ρ над плоскостью, где нет источников

поля, дается формулами

(6.3а)

(6.36)

где U и Ζ — значения потенциала и вертикальной составляющей

на заданной плоскости, ζ — расстояние точки Ρ до плоскости,

г—расстояние элемента плоскости dS до точки Р, и интегри-

рование распространяется на всю бесконечную плоскость.

В практике магниторазведки наблюдаемой величиной обыч-

но является вертикальная составляющая на поверхности Земли,

т. е. первая производная потенциала по вертикали, а искомыми

все три производные в любой точке пространства. Кроме того,

в некоторых случаях необходимо знать и вторые производные

потенциала или первые производные компонент поля. Поэтому

необходимо остановиться на выводе формул для первых и вто-

рых производных для точек, лежащих как на самой поверхности,

так и вне ее, при заданном распределении вертикальной состав-

ляющей на поверхности Земли.

Все эти формулы получаются непосредственно из формул

(6.3) путем их дифференцирования.

Действительно, дифференцируя (6. За) по координатам х, у

и ζ точки Ρ и принимая при этом во внимание, что Ζ не зависит

от этих координат, получим:

(6.4)

при этом

С другой стороны, формула (6.3а), являясь решением урав-

нения Лапласа, применима к любой функции, если она удовле-

11*

164 Методика интерпретации

[Гл. VI

творяет этому уравнению. Поэтому, применяя ее к составляю

щим Χ, Y, Z, которые также удовлетворяют уравнению Лапласа,

будем- иметь

Формулы (6.4) и (6.5) и являются формулами пересчета

магнитного поля с одной плоскости на другую.

Следует отметить, что если поле однородно, т. е. Χ, Y и Ζ

на всей бесконечной плоскости остаются постоянными, то в лю-

бой точке Ρ при любом значении ζ:

—Х,

—Υ

=Ζ.

Действительно, заменяя в формуле (6.5) dS = Idlda, где /

—

расстояние от эпицентра точки Ρ до любой точки на плоскости,

а α — угол между осью ξ и радиусом-вектором /, будем иметь

и аналогично для других составляющих.

Поэтому при наличии в составе магнитного поля на задан-

ной плоскости постоянной составляющей, при вычислении поля

на любом расстоянии ζ, эта составляющая целиком войдет в

искомые значения Х

, Υ

и Ζ

Такой же постоянной составляющей в искомых значениях

можно рассматривать и значение Ζ

в точке Ро, являющейся

проекцией точки Ρ на плоскости, так как Ζ

можно представить

как сумму Ζ

в точке Ро и приращения ΔΖ при подъеме на вы-

соту г. Поэтому можно написать:

(6.5)

(6.6)

но,

согласно уравнению

(6.5),

поэтому:

(6.7)

Формула г(6.7) носит название формулы Пуассона. Аналогичные

формулы будут для Хр и Ур.

Методы расчета производных

165

Формулы в таком виде заметно упрощают расчет, так как

избавляют от необходимости при всех операциях повторять

одно и то же число Z

В случае плоской задачи, когда U и зависят только от

двух переменных, например г и |, формула (6.7) принимает

более простой вид, так как интегрирование по третьей перемен-

ной η выполняется в квадратуре. Так, например, для составляю-

щих Ζ

будем иметь:

(6.8)

Соответственно такой же вид будут иметь и формулы для

(Х

-Хо) и (Υρ-Υ

Формулы для Хр и Υρ справедливы для точек не только вне

плоскости, но и на самой плоскости.

В этом случае, принимая точку Ρ на плоскости за начало

координат, будем иметьг

(6.9)

т. е., зная распределение Ζ на плоскости, можно определить

составляющие X и Y в любой точке этой плоскости.

Это,

казалось бы, освобождает от необходимости непосредст-

венного измерения других составляющих кроме вертикальной.

Однако в тех случаях, когда имеется аппаратура для измерения

и Z, предпочтительно производить измерения обоих элементов,

так как точность вычисления H и Ζ никогда не может быть срав-

нимой с точностью непосредственных измерений.

В большинстве случаев при исследовании аномалий прихо-

дится ограничиваться измерением лишь одной вертикальной со-

ставляющей, поэтому необходимость в расчете X и Y по указан-

ным формулам становится очевидной.

Для нахождения вторых производных рт потенциала следует

продифференцировать уравнение (6.4) по соответствующей ко

ординате.

àZp

Так, например, для нахождения следует взять производ-

ную по г от выражения для Z

, что дает

(6.10)

166

Методика интерпретации

[Гл.

Аналогичные

же

формулы получаются

для

остальных компо-

нент.

Для точки

на

плоскости,

где 2 = 0,

очевидно

(6.11)

Приближенные вычисления

Хр,

и Ζρ^

Практически

мы

имеем всегда

не

непрерывное распределение

Χ, Y и Ζ на

плоско-

сти,

точечное,

и не на

всей бесконечной плоскости,

лишь

на

некотором ограниченном участке. Поэтому точные формулы

(6.4)

должны быть заменены приближенными. Ограничимся рассмо-

трением расчета одной какой-либо составляющей, например

Для удобства выберем цилиндрическую систему координат

начало

ее

поместим

эпицентр точки

Р,

тогда

dS =

Idlda,

=ζ

-Η/

и -j = cos α,

поэтому формула

(6.4) для Ζ

примет

вид:

(6.12)

Разобьем внутренний интеграл

на

сумму двух интегралов

пределах

от 0 до

некоторого значения

/ = L и от L до оо, т. е.

(6.13)

Значение

представляет границу области интегрирования,

и по-

этому второй интеграл есть

та

погрешность, которую

мы

допу-

скаем, ограничиваясь конечным значением площади интегриро-

вания.

Обозначим

ее

через

ΔΖ

найдем пределы этой погрешности,

вычислив приближенно второй интеграл. Если обозначить через

Zj,

максимальное значение

Ζ на

круге радиуса

L, то

(6.14)

или

При достаточно большом значении

L по

сравнению

с ζ

относй-

ΔΖρ

тельная погрешность

-=—

будет:

Zj»

Методы расчета производных

167

(6.15)

Выбором границы интегрирования L, на которой Z

значи-

тельно меньше Z

>, можно уменьшить погрешность до любого

предела.

Вычисление производной непосредственно из кривой рас

пределе ни я Ζ по профилю производится по формулам конечных

разностей.

Одной из таких формул может служить формула Стирлинга

(6.16)

где Ζ_ι, Z+ь Ζ_2, Ζ+2 — значения Ζ на расстояниях Аде и 2Δ* по

обе стороны от точки, для которой производится вычисление.

Аналогичный вид будет иметь формула для градиента гори-

зонтальной составляющей

Для вычисления вертикальной составляющей Ζ на высоте ζ

удобнее пользоваться формулой

(6.7),

выраженной в полярных

координатах. Принимая за начало координат проекцию точки

Ρ на плоскость, будем иметь

где / и θ — полярные координаты какой-либо точки на плоскости.

Внутреннее интегрирование от 0 до 2π производится при по

стоянном значении /, и к нему можно применить теорему о сред

нем значении, т. е. написать:

2я 2я

(Z-Z

)dQ=(Z-Z

)

/<*θ = 2π(Ζ-Ζ

о о

где Ζ — среднее значение Ζ на круге радиуса /. Таким образом,

ее

Следовательно, чтобы найти Zj>, следует из точки О, являю

щейся проекцией точки Ρ на плоскость, провести ряд концентр и

168

Методика интерпретации

[Гл.

ческих окружностей радиусами

/ и

осреднить

Ζ на

каждой

из

этих окружностей,

затем произвести суммирование

по

формуле:

Интегральные выражения

для

нахождения магнитных

моментов

координат центра тяжести возмущающих пород

Для однородно намагниченных пород независимо

от их

фор-

мы

размеров однозначно определяются магнитные моменты

центр тяжести этих

тел,

если известно распределение магнитного

поля

на

поверхности Земли.

Определение магнитного момента. Магнитный потенциал

любого намагниченного тела определяется формулой Пуассона

где

У—

намагниченность тела,

dv—

элемент объема

г—рас-

стояние элемента

dv до

точки,

где

ищется потенциал,

интегри-

рование распространяется на.весь объем тела.

Эту

формулу

можно представить

виде

(6.17)

где

Поэтому

Умножим

обе

части этого выражения

на

элемент площади

dxdy = pdpda, где ρ = г sin θ, и

проинтегрируем

по

всей беско-

нечной плоскости,

т. е. по ρ от 0 до со, а по α от 0 до 2π.

Нетрудно

видеть,

что

первые

два

интеграла обращаются

нуль.

Так, на

пример, первый

из них

Интегральные выражения

169

Аналогично выразится

второй.

Поэтому

или, заменяя

г = R sec θ, ρ = R tg θ,

получим

(6.18)

где

—

составляющая магнитного момента

по оси г.

Аналогично выводятся соответствующие магнитные моменты

и М

которые получаются путем интегрирования

по

всей

площади выражении

х-^ =xZ и =ί/Ζ, т. е.

(6.19)

В случае вертикального намагничивания

= J

= 0, /

=/)

выражения магнитного момента будут:

(6.20>

Для двухмерной задачи формулы

(6.20)

принимают

вид:

(6.21)

Здесь μ—магнитный момент единицы длины тела бесконечного

простирания

по

горизонтальному направлению,

a μ

и μ

— со-

ставляющие

по

осям

χ и г.

При вертикальном намагничивании

(θ.22>

170

Методика интерпретации

[Гл.

Таким образом,

для

однородно намагниченных

тел

незави-

симо

от их

формы

размеров однозначно определяются магнит

ные моменты трехмерного тела

магнитный момент единицы

длины двухмерного тела.

Практически такое определение производится путем сумми-

рования произведений соответствующих средних значений под-

ынтегральных функций, входящих

выражение

(6.20) и (6.21),

на элементы площадок

AS. При

этом суммирование производит-

ся

по

площади

для

трехмерных

и по

линии

для

двухмерных ано-

малий

в тех

пределах,

которых

х, у и ζ

имеют значения боль-

шие,

чем

погрешности

их

измерения.

Для этого весь участок разбивается

на

прямоугольники

или

линии одинаковой длины,

и из

данных наблюдений находятся

средние значения

тех или

иных элементов

этом прямоуголь-

нике

или

отрезке длины.

Необходимо отметить,

что для

любого намагниченного тела

«справедливы соотношения:

(трехмерное тело),.

(двухмерное тело).

Для двухмерных

тел при

вертикальном

их

намагничивании

магнитный момент

единицы длины можно находить

по

более

простой формуле, которая получается

из

выражения

(5.61) для

вертикальной составляющей Η

=Ζ. Умножим

обе

части этого

выражения

на г

будем стремить

г к

бесконечности, тогда после

интегрирования

по

объему тела

В пределе

стремится

координате

х, a θ — к

нулю,

что

легко видеть

из рис. 77. В

таком случае

(6.23)

Хотя

эта

формула

и не

требует интегрирования

по оси х,

для

нахождения магнитного момента требуется лишь знание

величины

Ζ на

расстоянии

х,

которое должно быть большим,

однако точность определения

таким способом очень мала.

Покажем

это на

примере бесконечно длинного цилиндра

(нити полюсов),

для

которого

выражается формулой

(5.19)