Яновский Б.М. Земной Магнетизм. Том 2

Подождите немного. Документ загружается.

Прямая задача

для

двухмерного пространства

141

касается

другими породами. Если такой пласт намагничен

по

вертикальному направлению,

то

очевидно,

что

вдали

от

кон-

такта поле

под ним

будет постоянным

близким

нулю,

лишь

над контактом

оно

будет иметь заметные градиенты

заметную

величину.

Найдем составляющие напряженности магнитного поля

та-

кого пласта, воспользовавшись выражениями

(5.32), (5.33) для

и Z,

соответствующими верхней

нижней граням бесконечно

длинной призмы, изменив

в них

лишь пределы интегрирования.

После интегрирования получим

(5.35)

Легко видеть,

что над

контактом,

где х = О, Ζ = 0, а Η

имеет

максимальное значение.

При χ >· / обе

составляющие

Η и Ζ

стремятся

нулю.

Максимальное

минимальное значения Z-составляющей

имеют место

при χ = ± у/? (# +

/),

величина

их

Кривые

для R=\ и /=4,

соответствующие формулам

(5.35),

представлены

на рис. 69.

дН

Для данного случая производные

—^- и

также можно

рассматривать

как

компоненты поля однополюсных нитей. Диф-

ференцируя выражение

(5.35),

получим

(5.36)

Однако

этом случае

для

составляющей

положительно

за-

ряженная нить должна быть

на

нижнем ребре,

а для

составляю-

щей

Zi — на

верхнем. Соответственно, отрицательно заряжен-

ная нить

для Hi

должна быть

на

верхнем,

а для Z

— на

нижнем

ребре.

Наклонный пласт бесконечной длины. Более общим слу-

чаем двух предыдущих является случай, когда бесконечно длин-

ная призма имеет

своем сечении параллелограмм

намагни-

142

Магнитное поле

тел

[Гл.

ченна

любом направлении.

При

этом,

как и

раньше, будем

считать,

что

верхняя грань призмы расположена параллельна

земной поверхности.

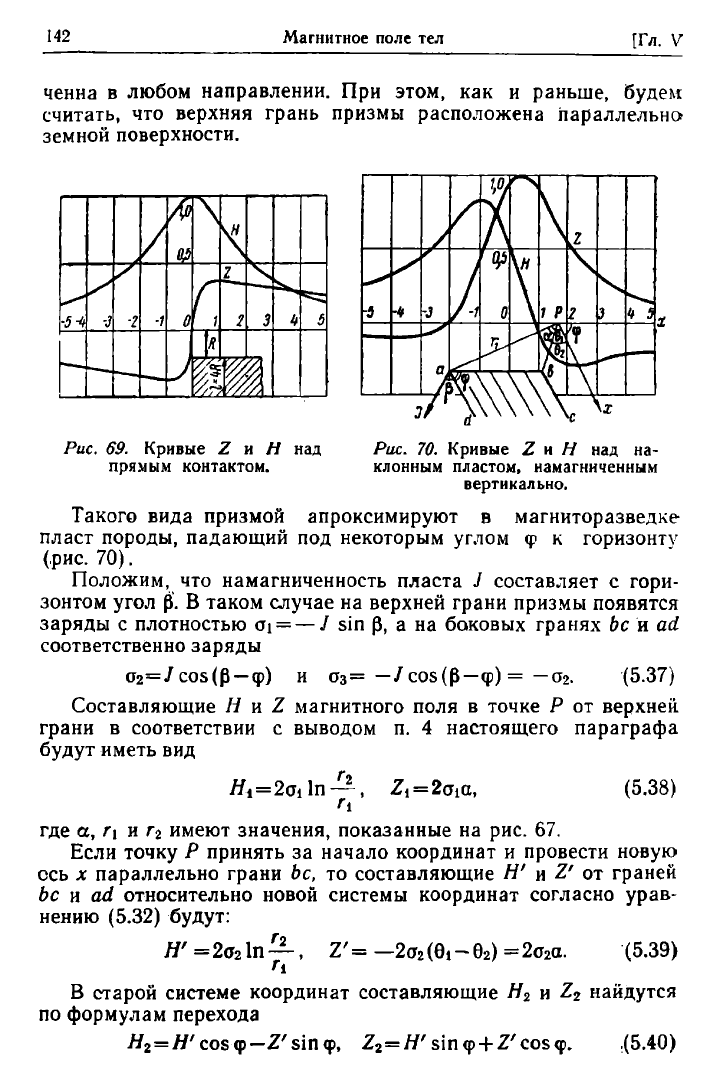
Рис.

69.

Кривые

Ζ и Η

прямым контактом.

над

Рис.

70.

Кривые

Ζ и Η над на-

клонным пластом, намагниченным

вертикально.

Такого вида призмой апроксимируют

магниторазведке

пласт породы, падающий

под

некоторым углом

φ к

горизонту

(рис.

70).

Положим,

что

намагниченность пласта

составляет

гори-

зонтом угол

0L В

таком случае

на

верхней грани призмы появятся

заряды

плотностью

σι =

—

sin β, а на

боковых гранях

be и ad

соответственно заряды

(5.37)

Составляющие

Я и Ζ

магнитного поля

точке

Ρ от

верхней

грани

соответствии

выводом

п. 4

настоящего параграфа

будут иметь

вид

(5.38)

где

а,

Г\

и г

имеют значения, показанные

на рис. 67.

Если точку

принять

за

начало координат

провести новую

ось

параллельно грани

be, то

составляющие

Я' и Z' от

граней

be и ad

относительно новой системы координат согласно урав-

нению

(5.32)

будут:

(5.39)

В старой системе координат составляющие

и Z

найдутся

по формулам перехода

(5.40)

Прямая задача

для

двухмерного пространства

Выражение составляющих

от

всей призмы найдем, если сло-

жим выражения

(5.38) и (5.40), т. е.

(5.41)

или

соответствии

формулами

(5.37),

заменяя

σι, 02, αϊ, r

их значениями:

(5.42)

Из

рис. 70, на

котором показан

ход

кривых

Ζ и H для

плас-

та, наклоненного

горизонту

под

углом

φ = 60°,

видно,

что на-

клон вызывает асимметрию обеих кривых, хотя нижняя гра-

ница находится

на

бесконечности.

По сравнению

вертикальным положением пласта,

кото-

рого

нигде

не

имеет отрицательных значений, наклонный

пласт дает вертикальную составляющую, которая проходит

через нуль

при х,

примерно

в два

раза большем глубины зале-

гания,

и при χ > 2R

принимает отрицательное значение.

Необходимо отметить,

что при

намагниченности пласта

вдоль

его

боковых граней магнитное поле будет тождественно,

с полем вертикального пласта.

Действительно, полагая

формулах

(5.42) β = φ,

получим

выражение, аналогичное

(5.33), так как

/sincp

= J

= о.

дН

Производные

от и для

наклонной призмы

соответ-

ствии

уравнением

(5.42)

выразятся формулами:

(5.43)

144

Магнитное поле

тел

[Гл.

Эти выражения представляют сумму полей, создаваемых

двумя наклонными пластинками бесконечного простирания

глубину, намагниченными

по

вертикали

расположенными

вдоль боковых граней пласта.

При

этом одна

из них

намагни-

чена

одном направлении,

другая

— в

противоположном.

Тонкая бесконечно длинная пластинка, залегающая

па-

раллельно земной поверхности. Тонкая пластинка (тонкий

пласт),

толщину которой можно рассматривать бесконечно

ма-

лой

по

сравнению

глубиной залегания, намагниченная верти-

кально, представляет собой совокупность большого числа «ли-

нейных диполей», магнитное поле которых было рассмотрено

п.

настоящего параграфа. Поэтому потенциал такой пластинки

представится

виде интеграла:

(5.44)

в котором подынтегральным выражением является потенциал

линейного диполя

или

бесконечного цилиндра

линейным маг-

нитным моментом, .равным

μάχ.

При

этом

Хо

обозначает абсцис-

су точки

Р, в

которой рассматривается потенциал,

2а—

ширина

пластинки.

После интегрирования получим:

откуда путем дифференцирования

по

соответствующим коорди-

натам находим значения горизонтальной

вертикальной состав-

ляющих:

или

(5.45)

(5.46)

Прямая

задача для двухмерного пространства 145

где /ι и г

имеют те же значения, что и в предыдущем случае

для призмы (см. рис. 67).

Такое же соотношение получается для составляющих маг-

нитного поля двух бесконечно длинных прямолинейных токов,

расположенных по краям пластинки, так как намагниченная

пластинка, представляющая двойной магнитный слой, эквива-

лентна по своим свойствам таким .токам. Из этого следует, что

если ширина пластинки велика по сравнению с глубиной ее за-

легания или расстояние между токами велико, то магнитное

поле над краем пластинки будет больше, чем над ее центром.

Действительно, анализируя уравнение

(5.46),

легко можно

показать, что вертикальная составляющая Ζ имеет один макси-

мум при лс=0, если а<узЯ. Если же а>уЗА, то максимальных

значений получается два: при х— ±У(#

+а

) —2R

~}/R

а ми-

нимальных— три: при х = 0 и при

На рис. 71 представле-

ны графики Ζ и Η для

а= 7г R и для а

3 R. В

первом случае

Я<УЗЯ,

мы действительно имеем

один максимум и два

минимума. Во втором

случае, когда а>уЗ R,

кривая Ζ дает два макси-

мума и три минимума.

Кроме того, характер-

ным для такого рода тел

является увеличение мак-

симума горизонтальной

составляющей при увели-

чении ширины пластины

2а. При ширине 2а боль-

ше некоторого значения максимум Η становится больше макси-

мума Ζ и располагается над краем пластинки.

Далее, сравнивая кривые для а =

R с кривыми линейного

диполя или цилиндра, можно видеть, что они мало отличаются

друг от друга, т. е. магнитное поле тонкой пластинки, ширина

которой меньше глубины залегания, практически не отличается

от линейного диполя.

Задачи, которые были рассмотрены выше, являются лишь

примерами того, как следует подходить к их решению. Однако,

сколько бы ни решать их, никогда нельзя исчерпать все формы,

которые могут быть в действительности.

Рис.

71. Кривые Ζ и Η над горизон-

тальной

пластиной.

1 — ширина пластины Ча R; 2 — ширина пластины

2а

- 6#.

>4б

Магнитное поле тел

[Гл.

Подробный обзор результатов решения прямых задач, имею-

щихся в литературе, можно найти в книге В. В. Колюбакина к

М. И. Лапиной [33].

8. Возможность применения плоской задачи. Пород с беско-

нечным простиранием в действительности не существует. Зале-

гающая порода всегда ограничена как в горизонтальном, так и

в вертикальном направлениях. Поэтому встает вопрос, в каких

случаях на практике можно пользоваться формулами, выведен-

ными в предыдущем параграфе, для тех или иных пород, имею-

щих бесконечные размеры по горизонтальному направлению,

т. е. применять плоскую задачу. Чтобы ответить" на этот вопрос,

необходимо сравнить магнитное поле породы или тела, имею-

щего бесконечное простирание, с телом конечных размеров. По-

этому рассмотрим в качестве примера магнитное поле «одно

полюсной линии» и «линейного диполя» конечной длины.

Так как для математической интерпретации аномалий, имею-

щих предельное простирание, достаточным является знание

магнитного поля вдоль профиля, проходящего через середину

и вкрест ее простирания, то, не нарушая общности задачи, бу-

дем искать магнитное поле вдоль линии, перпендикулярной к

однополюсной линии и линейному диполю и проходящей через

ее середину.

Для однополюсной линии конечной длины составляющие

напряженности поля можно представить, согласно уравнению

(5.22),

следующими интегральными выражениями:

где пределами интегрирования служат положительное и отри-

цательное значения полудлины полюсной линии. Значение

остальных символов то же самое, что и в п. 6. Значок / при

Χ, Y и Ζ поставлен с тем, чтобы отличить эти составляющие от

составляющих для бесконечно длинной линии.

Интегрируя в указанных пределах, получим:

(5.47>

Прямая задача

для

двухмерного пространства

147

(5.48)

при этом

= R

+ х

Сравнивая

их с

выражениями

(5.23) для

бесконечной линии,

мы

видим,

что

(5.49)

Следовательно, чтобы

Χι

были близкими

к X и Ζ,

необходимо

иметь полудлину полюсной линии значительно большей

г. Для

оценки отношения

-j, при

котором можно считать полюсную

линию эквивалентной бесконечной линии, разделим числитель

и знаменатель правой части

на /;

тогда, пренебрегая членами

высших порядков, будем иметь:

откуда

(5.50)

Если ограничиться погрешностью определения

Η и Ζ, не

пре-

вышающей

3% на

профиле, длиной

в три

раза большей глуби-

ны залегания

(х> SR), то на

основании этого равенства можно

определить длину полюсной линии

21,

которая будет эквива-

лентна бесконечной линии. Действительно,

из

уравнения

(5.50)

имеем:

откуда

т.

е.

длина полюсной линии должна быть

в 25 раз

больше глу-

бины залегания.

Такой

же

результат получается

и для

цилиндра, располо-

женного горизонтально

намагниченного вдоль диаметра. Маг-

нитный потенциал

цилиндра конечной длины, равной

21, в со-

ответствии

формулой*

(5.16)

представится:

148

Магнитное поле

тел

[Гл.

(5.51)

где значения букв

те же

самые,

что и в

формуле

(5.16).

Интег-

рируя, находим:

т.

е.

При небольших углах

а, т. е.

когда

/ > г, с

достаточной сте-

пенью точности:

или

(5.52)

Так

как ни

глубина залегания,

ни

длина залегающих пород

нам неизвестны,

то о

соотношении

их

можно делать заключения

лишь

на

основании

тех

карт изолиний вертикальной составляю-

щей, которые получаются

результате магнитной съемки.

По-

этому рассмотрим,

как

зависит распределение вертикальной

составляющей вдоль

вкрест простирания тела

от

соотношения

глубины залегания

длины тела, считая,

что оно

имеет форму

тонкой пластинки

одной линией полюсов.

Составляющая

Z; в

любой точке поверхности, очевидно,

будет

(5.53)

где

U и h —

расстояния

от

концов цилиндра

до

плоскости, про-

ходящей через точку

Ρ и

перпендикулярной

линии полюсов.

Выражая

1\ и

через углы

αϊ и а

производя интегриро-

вание, получим:

(5.54)

Для точек, расположенных

над

концами полюсной линии,

поэтому:

(5.55)

Графические методы решения

149

Над центром

же

полюсной линии:

(5.56)

Сравнивая

эти

выражения, получаем:

(5.57)

Так

как /

должно быть примерно

в 12 раз

больше

R, то,

заменяя

= 12/?,

будем иметь:

(5.58)

т.

е. над

концом полюсной линии должна проходить изодинама

со значением

Z, в два

раза меньшим,

чем над

центром аномалии.

Найдем далее,

на

каком расстоянии

χ от

центра

по

перпендику-

ляру

к оси

аномалии проходит

эта

изолиния.

Из

уравнения

(5.23)

имеем:

(5.59)

откуда

χ = R, т. е. на

расстоянии глубины залегания вертикаль-

ная составляющая имеет

то же

значение,

что и над

концом

по-

люсной линии. Отсюда следует,

что

если продольные размеры

изодинамы

Ζ,

разной половине максимального значения,

две-

надцать

раз

меньше поперечных,

то

аномалию можно рассма-

тривать

как

бесконечно длинную.

Графические методы решения прямой задачи

(метод палеток)

тех

случаях, когда нахождение потенциала

и его

основных

производных является невозможным, решение этой задачи про-

изводится методами приближенных вычислений, которые при-

водят

построению

π ал ето к,

пригодных

для

нахождения маг-

нитного поля какой-либо группы

тел.

Палетками

геофизике

называют прозрачные пластинки,

на

которые нанесены системы

кривых

или

прямых линий, рассчитанных теоретически. Нало-

жение такой палетки

на

экспериментальную кривую позволяет

во многих случаях получать требуемый результат

без

промежу-

точных вычислений.

Приближенные методы вычисления потенциала, создаваемо-

го телом

(в

случае трехмерной задачи)

или

плоской фигурой

(в случае двухмерной задачи) любой формы, заключаются

150

Магнитное поле

тел

[Гл.

разделении

их на

объемы

или

площади такой формы, которые

позволяют производить интегрирование

по ним в

конечном виде

через простейшие функции.

таком случае потенциал тела

или

фигуры будет суммой потенциалов

от

каждого объема

или

пло-

щадки. Потенциалы

от

пограничных объемов

или

площадок,

имеющих сложные формы, принимаются равными дробной

части потенциалов объемов

или

площадки правильной формы,

включающих пограничные объемы.

При

этом дробная часть

считается равной отношению граничного объема

или

площадки

к соответствующему объему

или

площадке правильной формы.

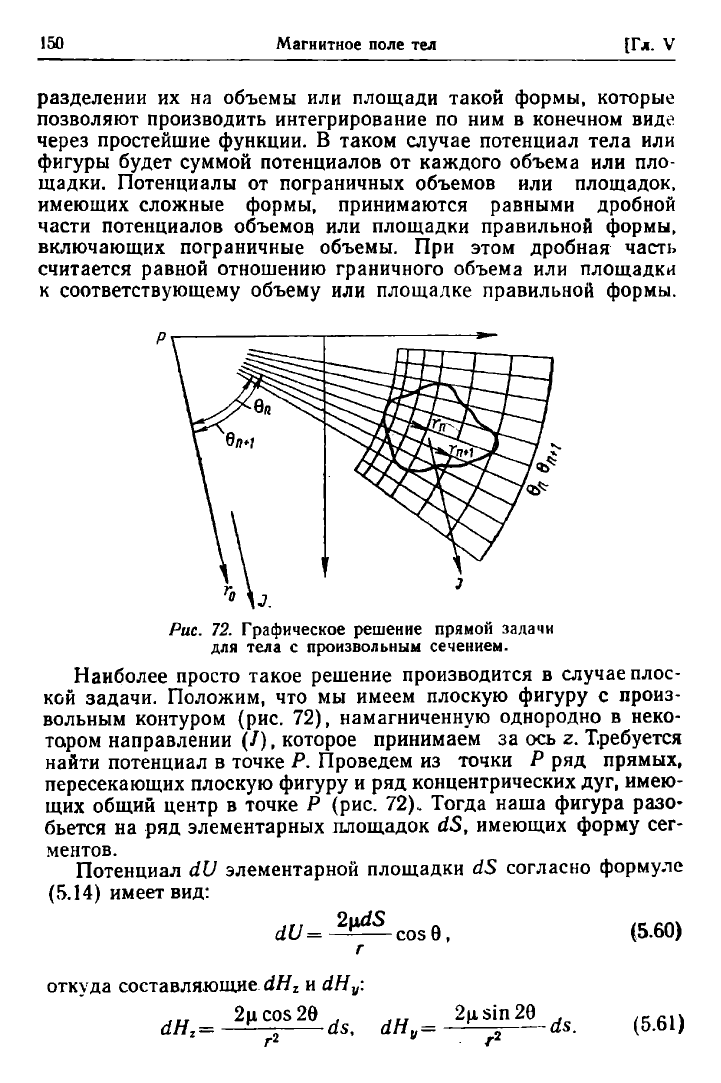
Рис.

72.

Графическое решение прямой задачи

для тела

произвольным сечением.

Наиболее просто такое решение производится

случае плос-

кой задачи. Положим,

что мы

имеем плоскую фигуру

произ-

вольным контуром

(рис. 72),

намагниченную однородно

неко-

тором направлении

(/),

которое принимаем

за ось ζ.

Требуется

найти потенциал

точке

Р.

Проведем

из

точки

Ρ ряд

прямых,

пересекающих плоскую фигуру

и ряд

концентрических

дуг,

имею-

щих общий центр

точке

Ρ (рис. 72).

Тогда наша фигура разо-

бьется

на ряд

элементарных площадок

dS,

имеющих форму сег-

ментов.

Потенциал

элементарной площадки

согласно формуле

(5.14)

имеет

вид:

(5.60)

откуда составляющие

и dH

(5.61)